数据结构第五课 -----二叉树的代码实现
作者前言
🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂
🎂 作者介绍: 🎂🎂
🎂 🎉🎉🎉🎉🎉🎉🎉 🎂
🎂作者id:老秦包你会, 🎂
简单介绍:🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂
喜欢学习C语言和python等编程语言,是一位爱分享的博主,有兴趣的小可爱可以来互讨 🎂🎂🎂🎂🎂🎂🎂🎂
🎂个人主页::小小页面🎂
🎂gitee页面:秦大大🎂
🎂🎂🎂🎂🎂🎂🎂🎂
🎂 一个爱分享的小博主 欢迎小可爱们前来借鉴🎂
二叉树的顺序结构实现
- **作者前言**
- 小知识
- 堆的实现
- 结构体
- 插入
- 删除
- 根节点
- 长度
- 是否为空
- TOP-K问题
- 堆排序
- 总结
小知识
完全二叉树的堆的创建时间复杂度
假设我们随意给出一个长度为n的数组,如果我们要建堆,最坏的情况就是全部节点都要向下调整
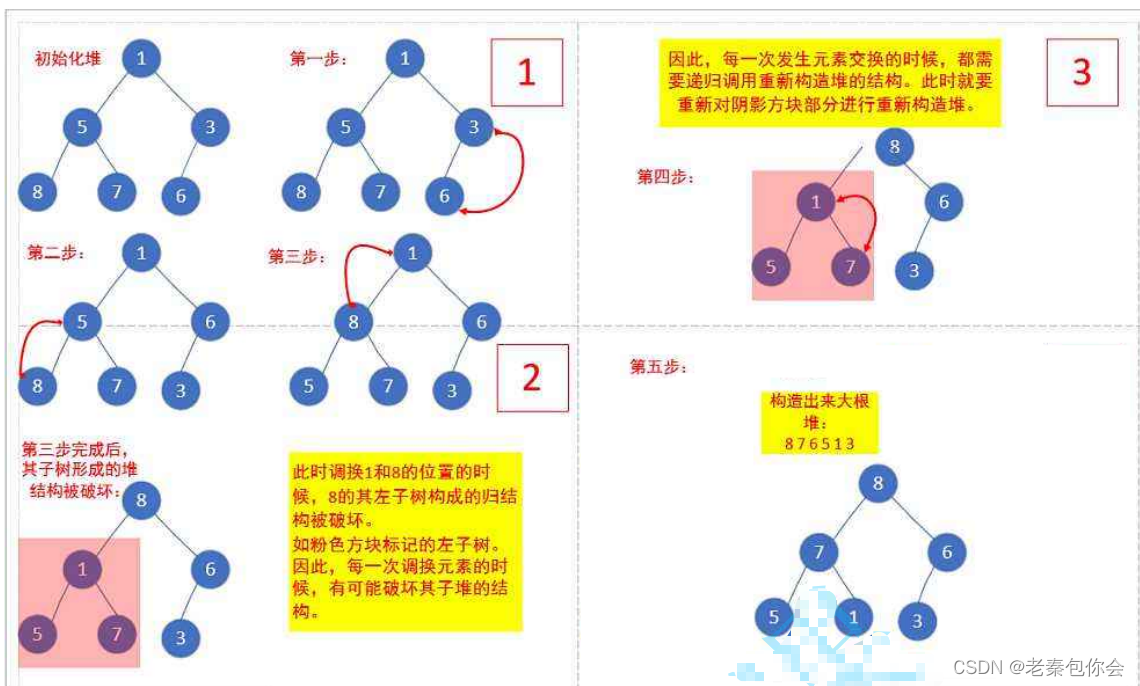
我们可以当完全二叉树是满二叉树进行计算
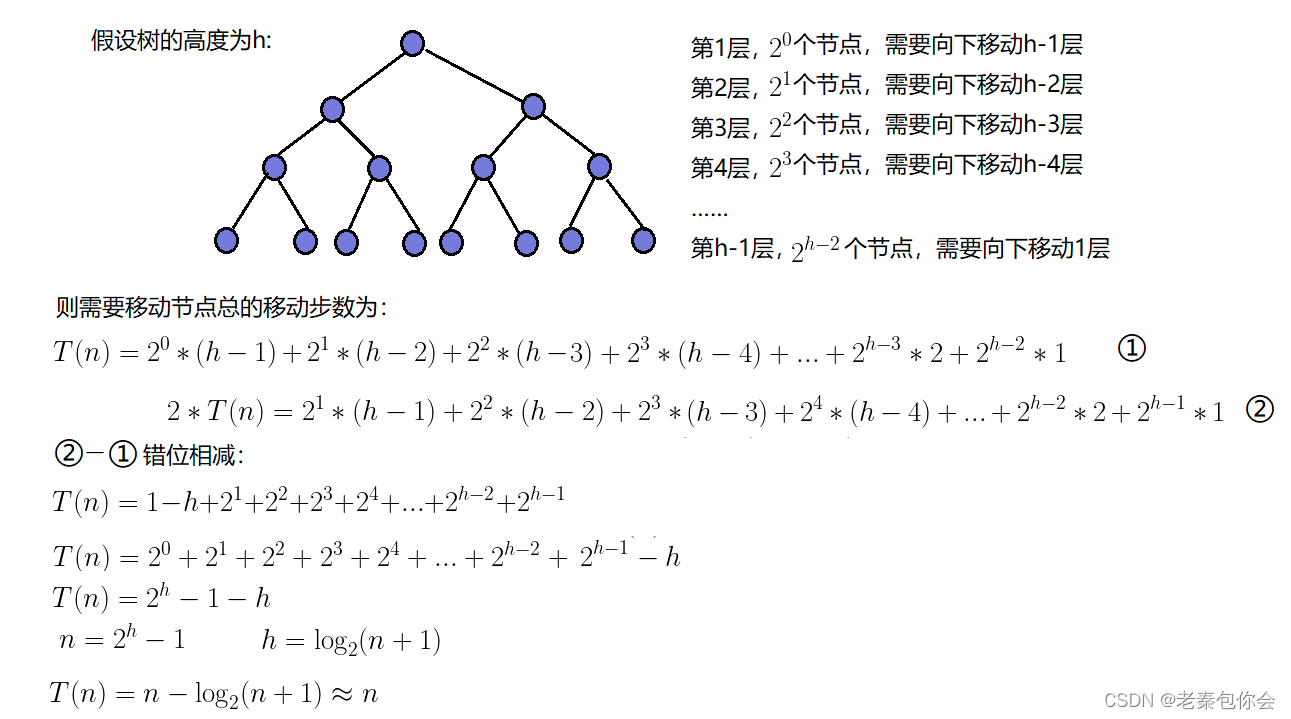
我们需要统计全部节点的移动次数,最终全部计算出 2^h -1 - h,因为是每个节点要往下移动一个高度次, 满二叉树是 的节点数 N = 2 ^h - 1 所以 h = log(N +1),代入 2^h -1 - h得出n - log(n+1) 大约就是n次 而每个节点的时间复杂度是大约是O(log(N))(每个节点向下调整高度次).这个就是向下调整的时间复杂度O(N)
向上调整的时间复杂度
二叉树的最后一层占据所有节点的一半
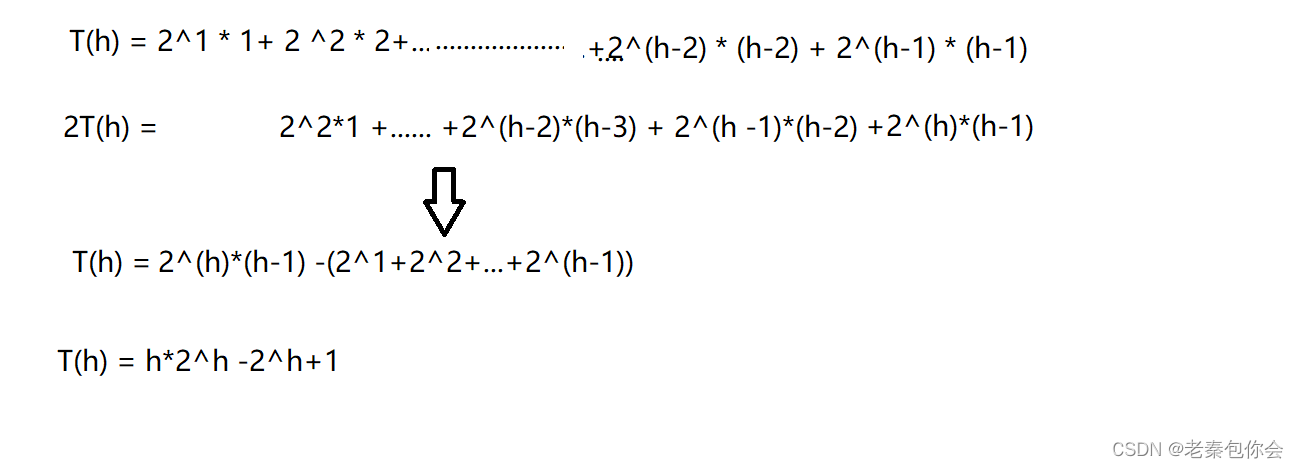
最终化简就是T(n) = (n+1)*(log(n+1) - 1) +1 -n 大概就是O(N *log(N))
堆的实现
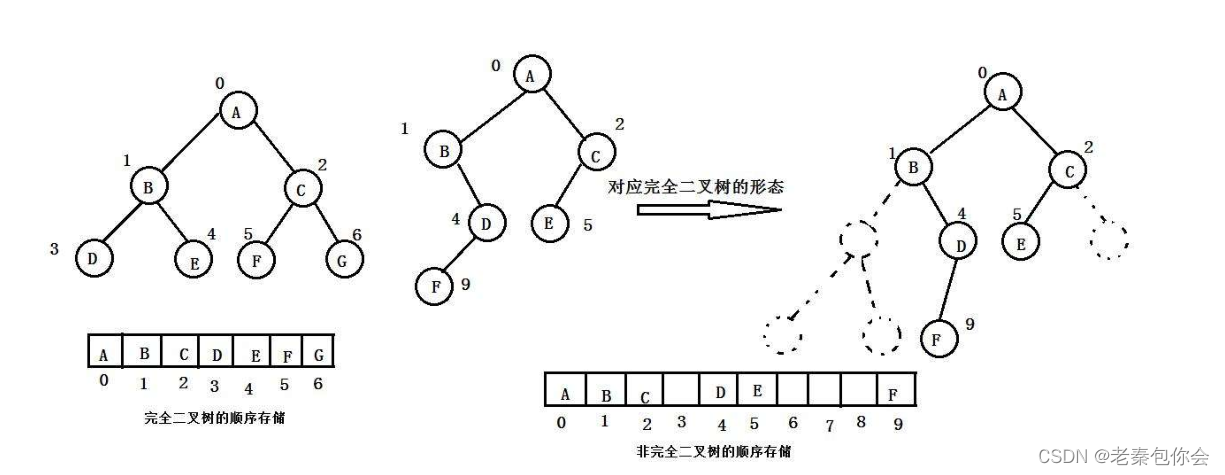
可以发现我们的要想实现二叉树就得借助顺序表来进行操作,因为二叉树是逻辑结构,我们要想实现就得利用物理结构,也就是堆 ,堆有大小堆的区分,下面我以小堆来实现
结构体

这里是利用顺序表来存储,所以结构和顺序表是一样的,但是本质上还是二叉树
typedef int HDataType;
typedef struct Heap
{HDataType* tree;int size;int capacity;
}Heap;
插入
思路:我们先插入最后一个,然后向上调整,因为我们是小堆,要保证每个父亲<= 孩子
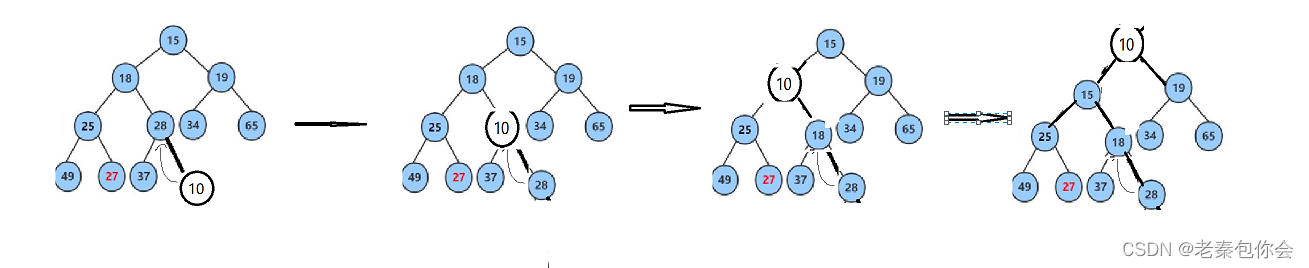
这里我们要注意不能越界,
//向上调整
void adjust(HDataType* tree, int Hsize)
{int child = Hsize - 1;int parent = (Hsize - 1 - 1) / 2;while (child > 0){if (tree[child] < tree[parent]){HDataType b = tree[child];tree[child] = tree[parent];tree[parent] = b;child = parent;parent = (child - 1) / 2;}elsereturn;}
}
// 插入
void Heappush(Heap* obj, HDataType elemest)
{//判断释放满if (obj->size == obj->capacity){obj->capacity = (obj->capacity == 0 ? 4 : obj->capacity * 2);HDataType * tmp = realloc(obj->tree, sizeof(Heap) * obj->capacity);if (tmp == NULL){perror("realloc");return;}obj->tree = tmp;}obj->tree[obj->size++] = elemest;//开始检查是否大于父节点adjust(obj->tree, obj->size);}
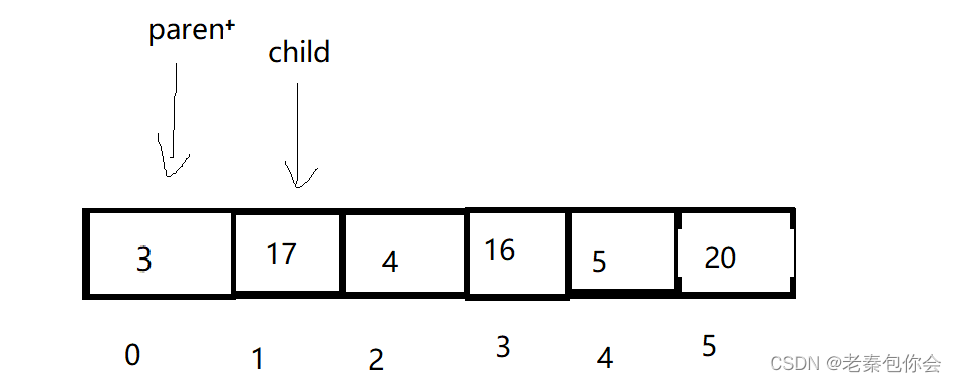
我们主要就是考虑 根节点和自己的孩子这里,是有可能越界的
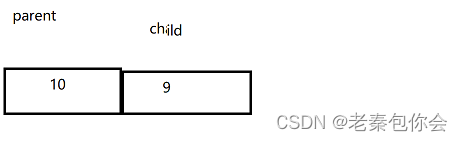
如图,可以利用child == 0来结束,
删除
这里的删除和前面我们学习过的顺序表和链表的删除不太一样,这里的删除是要删除二叉树的根节点,删除后又要构成一样的小堆
思路: 根节点和最后一个叶节点进行交换,然后删除叶节点(新的叶节点),交换后的根节点(新的根节点),然后让左右孩子进行比较大小,比较出最小值,然后再和根节点进行比较,如果根节点大于,就交换,然后依次循环直到符合小堆, 如果小于或者等于则不用调整,但是因为我们是把最后一个叶节点交换,交换的节点可能会大于等于,这种情况可以忽略,但是思路还是可以借鉴,
需要注意的是我们交换是循环进行的要找到结束条件
// 删除 (删除根节点)
void HeapPop(Heap* obj)
{assert(obj);assert(obj->size > 0);//两节点交换HDataType elemest = obj->tree[0];obj->tree[0] = obj->tree[obj->size - 1];obj->tree[obj->size - 1] = elemest;obj->size--;//向下调整int parent = 0;int child = parent * 2 + 1;if (parent * 2 + 1 < obj->size && parent * 2 + 2 < obj->size && obj->tree[parent * 2 + 1] > obj->tree[parent * 2 + 2] ){child = parent * 2 + 2;}while (child < obj->size){//判断孩子和父亲的大小if (obj->tree[parent] > obj->tree[child]){//两节点交换HDataType elemest = obj->tree[parent];obj->tree[parent] = obj->tree[child];obj->tree[child] = elemest;parent = child;}elsebreak;child = parent * 2 + 1;if (parent * 2 + 1 < obj->size && parent * 2 + 2 < obj->size && obj->tree[parent * 2 + 1] > obj->tree[parent * 2 + 2]){child = parent * 2 + 2;}}}
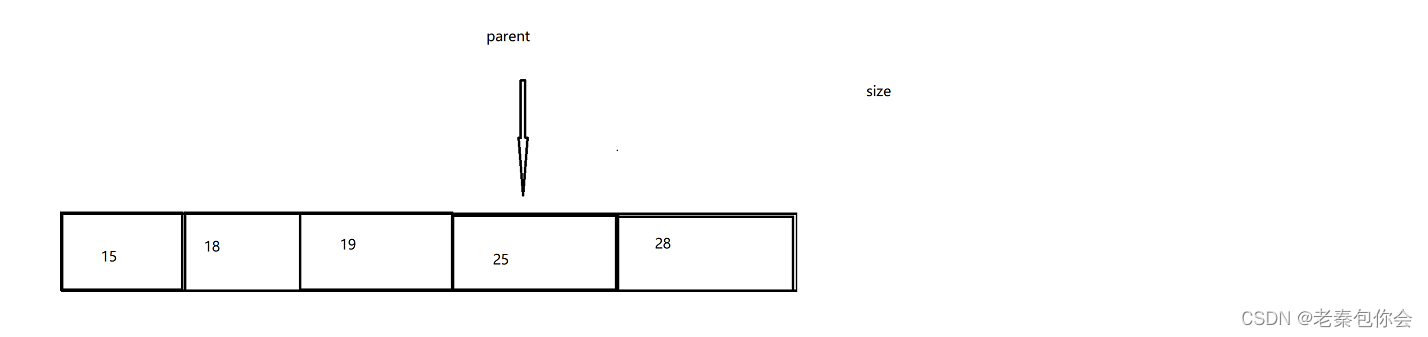
我们可以判断child是否大于等于size,,因为我们的思路就是要找到叶节点,我们只需child大于等于size就停止循环
根节点
// 根
HDataType HeapTop(Heap* obj)
{assert(obj);assert(obj->size > 0);return obj->tree[0];
}
长度
// 长度
size_t HeapSize(Heap* obj)
{assert(obj);return obj->size;
}
是否为空
//是否为空
bool HeapEmpty(Heap* obj)
{assert(obj);return obj->size == 0;
}
TOP-K问题
TOP-K问题: 即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
在N个数中找出前K个大的数(N远大于K)
- 思路: 把N个数创建成大堆,然后pop K次
这种算法的时间复杂度是 N *log(N) + K *log(N),每个节点向下调整
最终大约是O(N *log(N))
这种算法还是有差异
如果N是100亿, k = 10, 一个整形4个字节
那么我们就需要400亿字节,也就大约40G内存,我们电脑内存最多就32G,这个方法行不通 - 思路:
1.读取N个数的K个,创建一个K个数的小堆,
2.然后依次把剩下的N-K个数进行和堆顶比较,如果大于堆顶就顶替堆顶,然后向下调整形成小堆,
注意的是我们是要大于堆顶的数顶替原来的堆顶,不是让小的顶替, 我们知识借鉴了小堆的思路,并不是完全是按照小堆的思路走
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
void exchange(int *a, int *b)
{int e = *a;*a = *b;*b = e;
}
void PrintTop(int n)
{//创建一个n个数的小堆FILE* pf = fopen("./test.txt", "r");if (pf == NULL){perror("fopen");return 1;}int* Heap = (int*)malloc(sizeof(int) * n);int i = 0;for (i = 0; i < n; i++){int elemest;fscanf(pf, "%d", &elemest);Heap[i] = elemest;//向上调整int child = i;int parent = (child - 1) / 2;while (child > 0){if (Heap[child] < Heap[parent]){exchange(&Heap[child], &Heap[parent]);}elsebreak;child = parent;parent = (child - 1) / 2;}}// 继续读取下面的数据int ch = 0;while ( fscanf(pf, "%d", &ch) != EOF){if (ch <= Heap[0]){continue;}Heap[0] = ch;//向下调整int parent = 0;int child = parent * 2 + 1;while (child < n){if (child + 1 < n && Heap[child] > Heap[child + 1]){child += 1;}if (Heap[child] < Heap[parent])exchange(&Heap[child], &Heap[parent]);elsebreak;parent = child;child = parent * 2 + 1;}}//打印数据for (i = 0; i < n; i++){printf("%d ", Heap[i]);}free(Heap);fclose(pf);
}
void random(int n)
{FILE* pf = fopen("./test.txt", "w");if (pf == NULL){perror("fopen");return 1;}srand(time(NULL));int i = 0;for (i = 0; i < 10000; i++){fprintf(pf, "%d\n", (rand() + i) % 100000);}fclose(pf);
}int main()
{int n = 10;PrintTop(n);return 0;
}上面的代码中的建堆的代码可以使用插入小堆然后进行向上调整的方法,还有一种方法是假设一棵二叉树的
左右子树都是大堆或者小堆,然后我们只需进行根节点和左右子树点进行调整
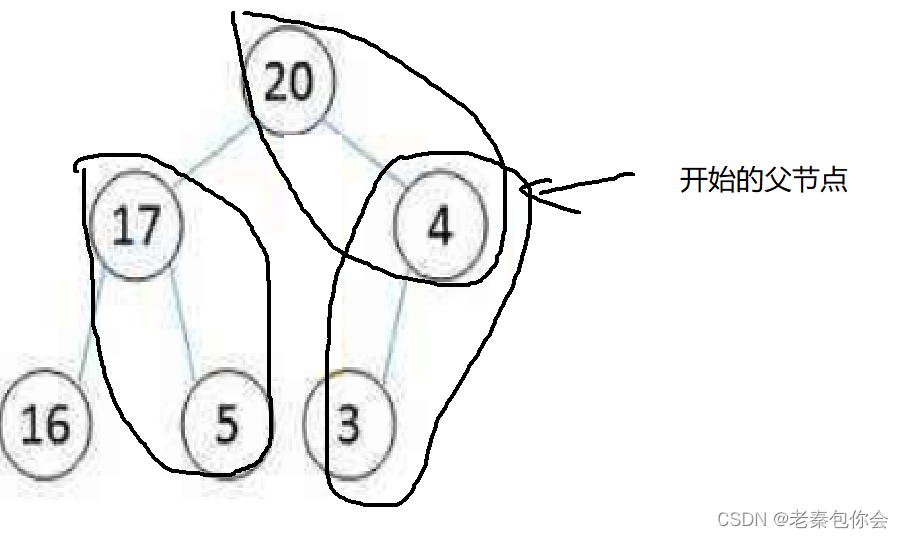
我们只需对最后叶节点的父节点开始进行向下调整,然后依次往下,
// 第二种方法//从最后一个节点的父亲开始向下调整,我们创建的是小堆 ,for (int i = (n - 1 - 1) / 2; i >= 0; i--){//向下调整int parent = i;int child = parent * 2 + 1;while (child < n){if (child + 1 < n && Heap[child] > Heap[child + 1]){child += 1;}if (Heap[child] < Heap[parent])exchange(&Heap[child], &Heap[parent]);elsebreak;parent = child;child = parent * 2 + 1;}}
这种算法的效率更高,第一种方法是我们慢慢学习了堆总结出来的,先插入值进堆,然后向上调整,这样很蛮烦
但是这种方法从一开始就是左右子树就是大堆或者小堆,然后只需进行根节点的向下调整就可以,这个是递归思想的一种体现
堆排序
升序排序建大堆 ,降序排序建小堆
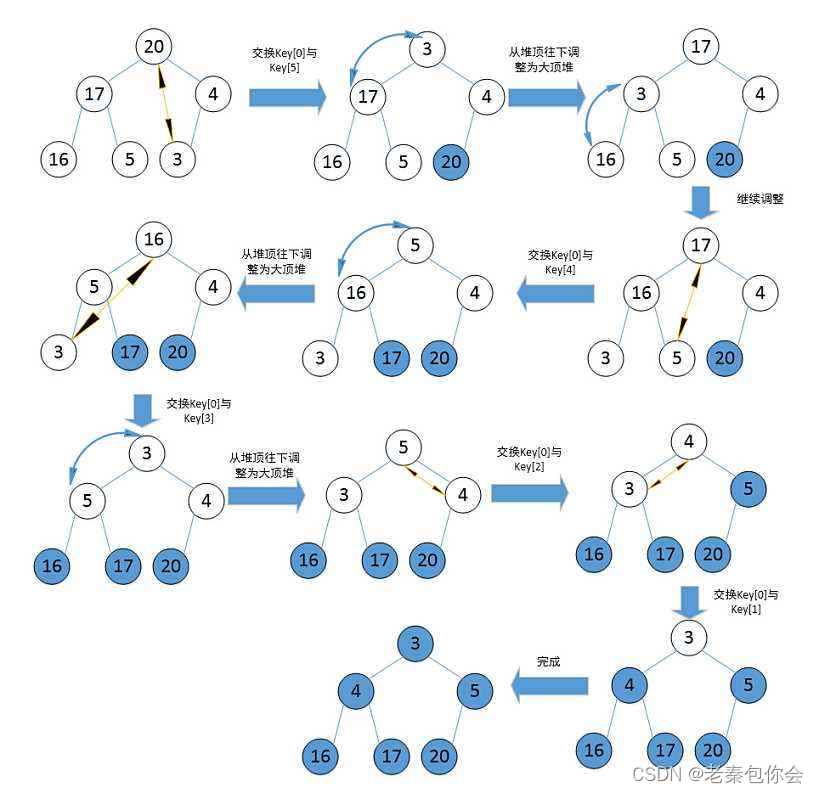
思路: 先 根节点和最后一个叶节点进行交换,这样就可以把最大的数放在数组的末尾,然后长度再减1
依次循环往下直到长度为1,或者下标为0就停止
#include<stdio.h>
typedef int Heapdata;
void exchange(Heapdata *a, Heapdata *b)
{Heapdata e = *a;*a = *b;*b = e;
}
void Heapsort(Heapdata* heap, int size)
{//建大堆int i = 0; for (i = 1; i < size; i++){//向上调整int child = i;int parent = (child - 1) / 2;while (child > 0){if (heap[child] > heap[parent]){//交换exchange(&heap[child], &heap[parent]);child = parent;parent = (child - 1) / 2;}elsebreak;}}//开始升序排序while (size > 0){// 根节点和最后一个叶节点交换exchange(&heap[0], &heap[--size]);//向下调整int parent = 0;int child = parent * 2 + 1;while (child < size){if (child + 1 < size && heap[child] < heap[child + 1]){child += 1;}if (heap[child] > heap[parent])exchange(&heap[child], &heap[parent]);elsebreak;parent = child;child = parent * 2 + 1;}}}
int main()
{Heapdata a[] = { 2,1,48,5,2,4,7,5,63,8 };int size = sizeof(a) / sizeof(a[0]);//堆排序Heapsort(a, size);return 0;
}
总结
这里简单介绍了堆 堆排序和Top K问题,还介绍了向下调整的时间复杂度和向上调整的时间复杂度
相关文章:

数据结构第五课 -----二叉树的代码实现
作者前言 🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂 🎂 作者介绍: 🎂🎂 🎂 🎉🎉🎉…...
工程师)
优橙内推北京专场——5G网络优化(中高级)工程师
可加入就业QQ群:801549240 联系老师内推简历投递邮箱:hrictyc.com 内推公司1:西安长河通讯有限责任公司 内推公司2:北京电旗通讯技术股份有限公司 内推公司3:润建股份有限公司 西安长河通讯有限责任公司 西安长河…...
Mysql DDL语句建表及空字符串查询出0问题
DDL语句建表 语法: create table 指定要建立库的库名.新建表名 (... 新建表的字段以及类型等 ...)comment 表的作用注释 charset 表编译格式 row_format DYNAMIC create table dev_dxtiot.sys_url_permission (id integer …...

深入ArkTS:应用状态管理与LocalStorage装饰器详解【鸿蒙专栏-11】
文章目录 ArkTS 应用状态管理详解LocalStorage: 页面级 UI 状态存储使用规则概述:装饰器详解:限制条件:使用场景:1. 应用逻辑使用 LocalStorage2. 从 UI 内部使用 LocalStorageArkTS 应用状态管理进阶LocalStorage 装饰器详解1. @LocalStorageProp2. @LocalStorageLink观察…...

管理Android12系统的WLAN热点
大家好!我是编码小哥,欢迎关注,持续分享更多实用的编程经验和开发技巧,共同进步。 要创建一个APK管理Android 12系统的WLAN热点,你需要遵循以下步骤: 1. 获取必要的权限和API访问权限。在AndroidManifest.xml文件中添加以下权限: ```xml <uses-permission android:…...

从0开始学习JavaScript--JavaScript 中 `let` 和 `const` 的区别及最佳实践
在JavaScript中,let 和 const 是两个用于声明变量的关键字。尽管它们看起来很相似,但它们之间有一些重要的区别。本篇博客将深入探讨 let 和 const 的用法、区别,并提供一些最佳实践,以确保在代码中正确使用它们。 let 和 const …...
【上海大学数字逻辑实验报告】二、组合电路(一)
一、 实验目的 熟悉TTL异或门构成逻辑电路的基本方式;熟悉组合电路的分析方法,测试组合逻辑电路的功能;掌握构造半加器和全加器的逻辑测试;学习使用可编程逻辑器件的开发工具 Quartus II设计电路。 二、 实验原理 异或门是数字…...

lodash中foreach踩坑
什么是lodash Lodash 是一个 JavaScript 实用工具库,提供了很多用于处理数据、简化开发等方面的功能。它提供了一组常用的工具函数,用于处理数组、对象、字符串等常见数据结构,同时也包含了一些函数式编程的工具。对于前端开发来说ÿ…...
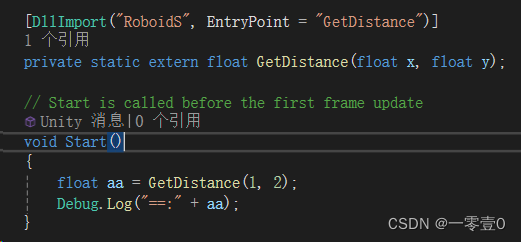
Unity C++交互
一、设置Dll输出。 两种方式: 第一:直接创建动态链接库工程第二:创建的是可执行程序,在visual studio,右键项目->属性(由exe改成dll) 二、生成Dll 根据选项Release或Debug,运行完上面的生成解决方案后…...
人工智能-优化算法之动量法
对于嘈杂的梯度,我们在选择学习率需要格外谨慎。 如果衰减速度太快,收敛就会停滞。 相反,如果太宽松,我们可能无法收敛到最优解。 泄漏平均值 小批量随机梯度下降作为加速计算的手段。 它也有很好的副作用,即平均梯度…...

【MySQL】InnoDB中的索引
目录标题 索引底层的数据结构:B树B树与B树的区别InnoDB与MyISAM在B树使用索引结构的不同? 聚簇索引非聚簇索引联合索引 B树索引适用的条件查询全值匹配匹配左边的列匹配列前缀匹配范围的值精确匹配某一列并范围匹配另外一列避免使用隐式转换 排序必须按照…...
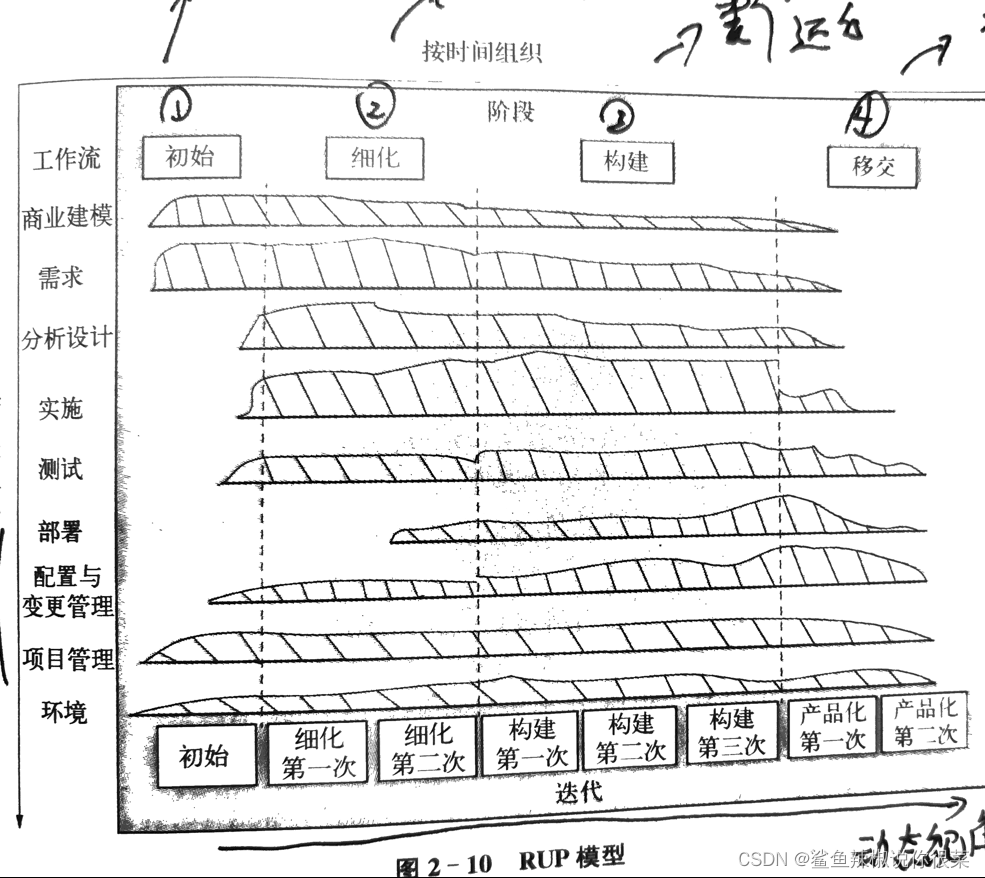
《软件工程原理与实践》复习总结与习题——软件工程
软件生命周期 软件生命周期分为三个时期、八个阶段 软件定义时期: 1)问题定义阶段:要解决什么问题 2)可行性研究阶段:确定软件开发可行 3)需求分析阶段:系统做什么 软件开发时期:…...

软工2021上下午第六题(组合模式)
阅读下列说明和Java代码,将应填入(n)处的字句写在答题纸的对应栏内。 【说明】 层叠菜单是窗口风格的软件系统中经常采用的一种系统功能组织方式。层叠菜单中包含的可能是一个菜单项(直接对应某个功能),也可…...

在Spring Boot中使用不同的日志
前言,本篇就是介绍在Java中使用相关的日志,适合初学者看,如果对这篇不感兴趣的可以移步了,本篇主要围绕我们Java中的几种日志类型,也说不上有多深入,算的上浅入浅出吧,如果你有一段时间的开发经…...

运维知识点-openResty
openResty 企业级实战——畅购商城SpringCloud-网站首页高可用解决方案-openRestynginxlua——实现广告缓存测试企业级实战——畅购商城SpringCloud-网站首页高可用解决方案-openRestynginxlua——OpenResty 企业级实战——畅购商城SpringCloud-网站首页高可用解决方案-openRes…...
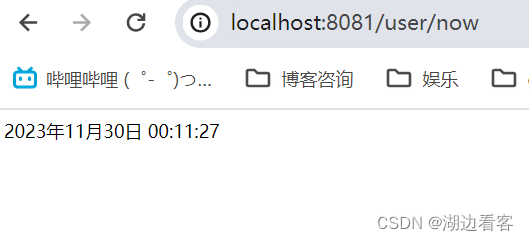
微服务中配置Nacos热更新
启动Nacos startup.cmd -m standalone 在IDE中启动服务 打开nacos管理后台并选择配置列表 创建配置(这里以日期格式为例) 因为这里配置的是userservice的服务,所以在userservice服务的pom文件中引入依赖 配置一个bootstrap.yml文件 注意这里bootstrap文件中配置过的内容,在app…...
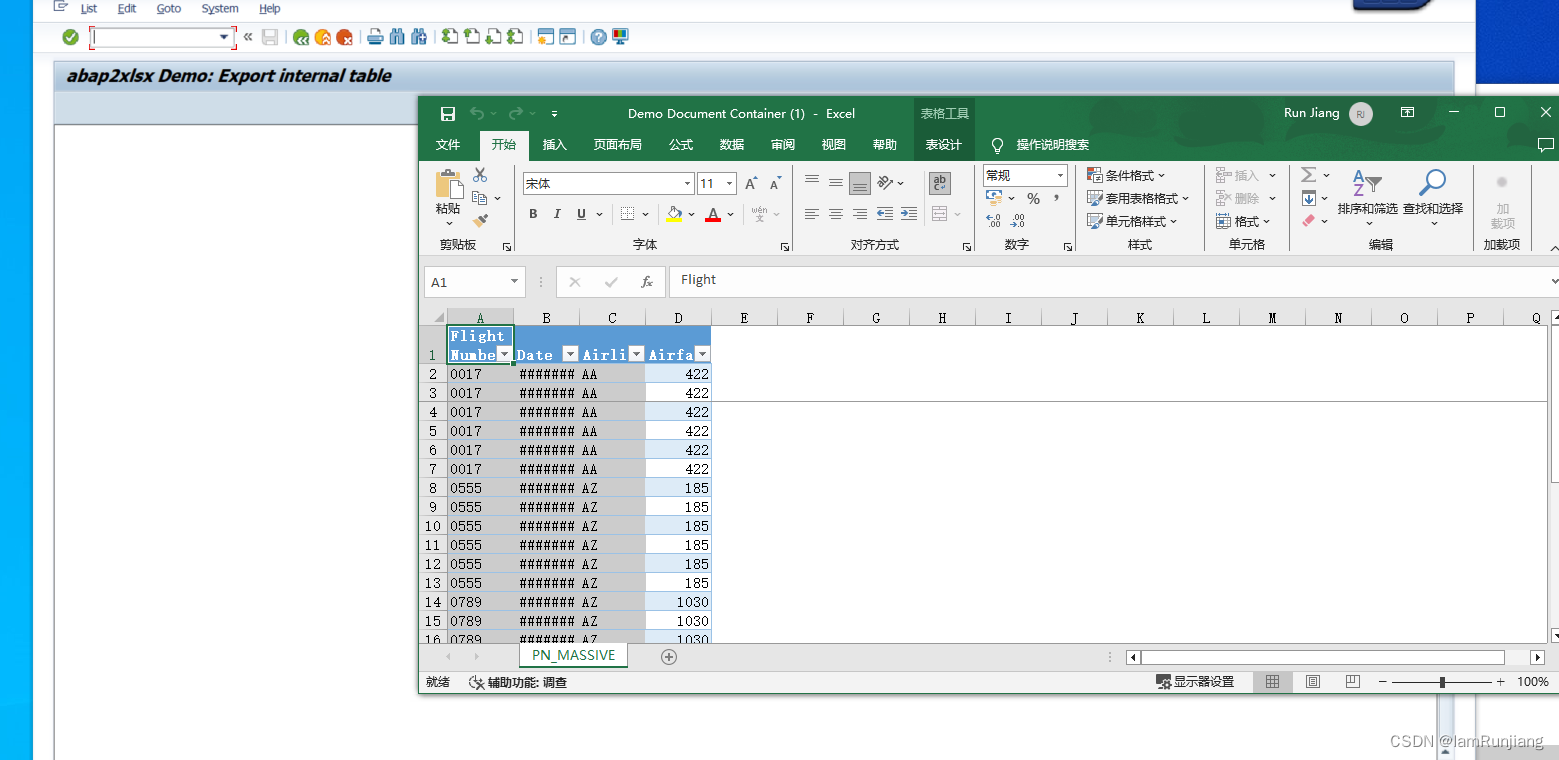
ABAP2XLSX 的安装和demo
ABAP2XLSX 是一个git上面的很好用的工具,它可以帮助abaper们更方便,更简单的生成各种各样复杂的自定义的excel,以满足各企业的信息化建设 在安装这个之前,请先查看之前的博客,去安装abapgit abap2xlsx地址࿱…...
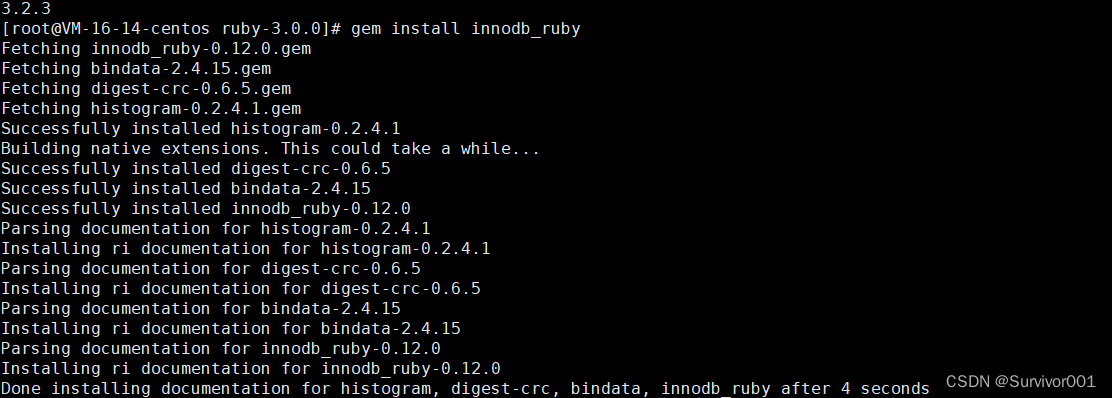
记一篇Centos7安装innodb_ruby
安装innodb_ruby过程非常坎坷,这里记录下安装过程,有些坑当时没有记录下来,主要把完成安装过程就记录下来 yum安装ruby默认的会安装ruby2.0.0版本,但是在安装innodb_ruby时,会报错,提示至少需要2.4版本以上…...
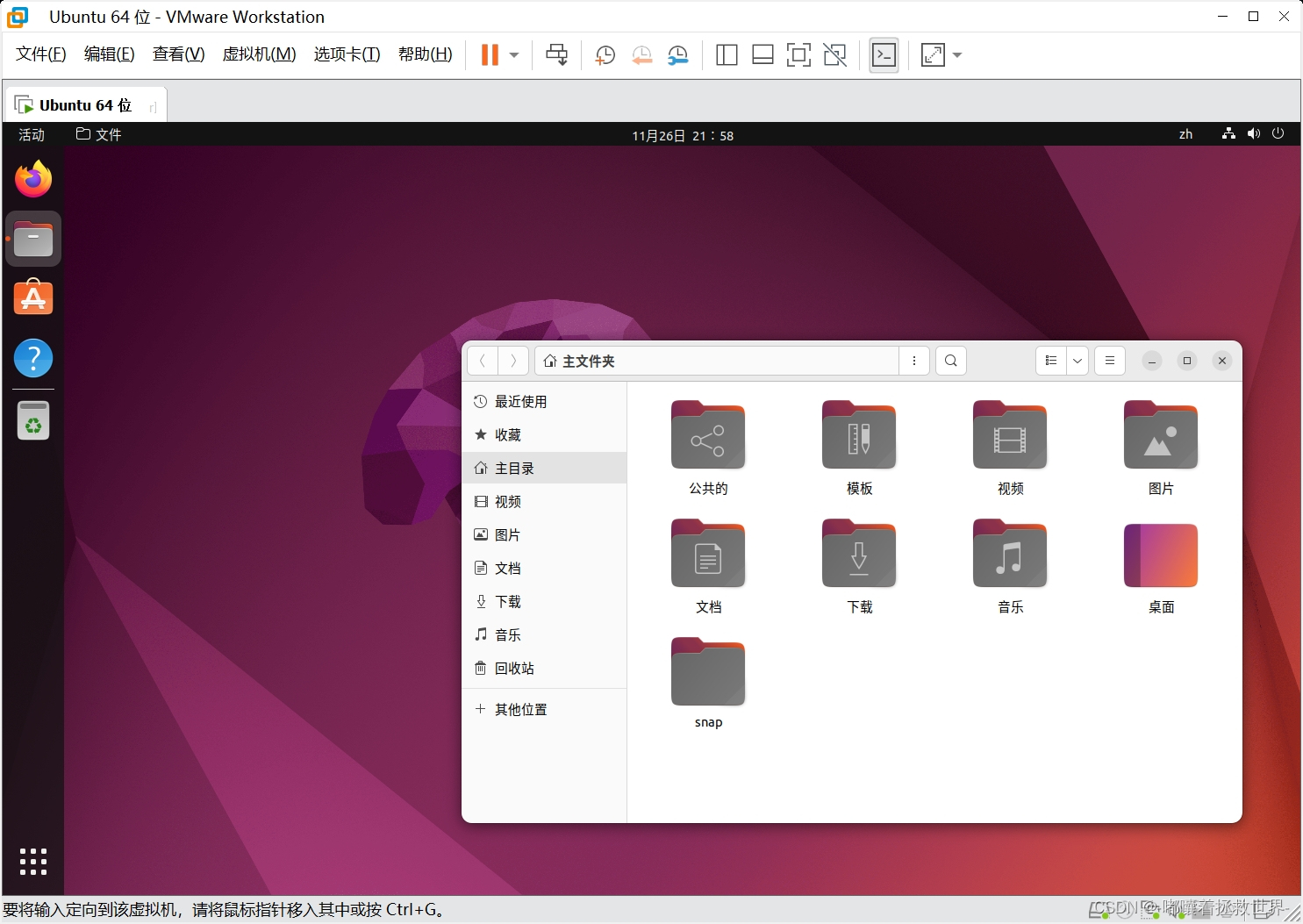
VMware虚拟机安装和使用教程(附最新安装包+以ubuntu为例子讲解)
目录 一、VMware Workstation 17 Pro 简介 二、新功能与改进 三、安装教程 3.1、下载安装包 3.2、运行安装包 四、创建虚拟机 五、启动虚拟机 六、总结与展望 一、VMware Workstation 17 Pro 简介 VMware Workstation 17 Pro是VMware公司为专业用户打造的一款虚拟化软件…...

c语言 / 指针错误的几种情况
1.未初始化的指针,直接释放 int *p; //计算机随机指向一片内存 2.free一个指针,指针没有指向NULL,直接使用 int *p(int *)malloc(sizeof(int)); free(p); //p依旧指向释放前内存的地址, 但是这片内存已经被释放, 被其他变量重新使用, 正…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
