【数据挖掘】国科大刘莹老师数据挖掘课程作业 —— 第三次作业
Written Part
1. 基于表 1 1 1 回答下列问题(min_sup=40%, min_conf=75%):
| Transaction ID | Items Bought |
| 0001 | {a, d, e} |
| 0024 | {a, b, c, e} |
| 0012 | {a, b, d, e} |
| 0031 | {a, c, d, e} |
| 0015 | {b, c, e} |
| 0022 | {b, d, e} |
| 0029 | {c, d} |
| 0040 | {a, b, c} |
| 0033 | {a, d, e} |
| 0038 | {a, b, e} |
表 1 数据集
-
使用 Apriori 算法确定全部的频繁项集。
Apriori 算法执行过程如图 1 1 1 所示。

图 1 Apriori
可以看出,频繁项集有 {a},{b},{c},{d},{e},{ab},{ad},{ae},{be},{de},{ade}。
-
计算关联规则的置信度,并判断这些置信度是否具有对称性。
C o n f i d e n c e ( a ⇒ d e ) = 4 7 C o n f i d e n c e ( d ⇒ a e ) = 4 6 C o n f i d e n c e ( e ⇒ a d ) = 4 8 C o n f i d e n c e ( a d ⇒ e ) = 4 4 C o n f i d e n c e ( a e ⇒ d ) = 4 6 C o n f i d e n c e ( d e ⇒ a ) = 4 5 {\rm Confidence}(a\Rightarrow de) = \frac{4}{7} \\ {\rm Confidence}(d\Rightarrow ae) = \frac{4}{6} \\ {\rm Confidence}(e\Rightarrow ad) = \frac{4}{8} \\ {\rm Confidence}(ad\Rightarrow e) = \frac{4}{4} \\ {\rm Confidence}(ae\Rightarrow d) = \frac{4}{6} \\ {\rm Confidence}(de\Rightarrow a) = \frac{4}{5} Confidence(a⇒de)=74Confidence(d⇒ae)=64Confidence(e⇒ad)=84Confidence(ad⇒e)=44Confidence(ae⇒d)=64Confidence(de⇒a)=54
显然,不满足对称关系。 -
确定强关联规则。
其中只有 C o n f i d e n c e ( a d ⇒ e ) ≥ {\rm Confidence}(ad\Rightarrow e)\ge Confidence(ad⇒e)≥ min_conf, C o n f i d e n c e ( d e ⇒ a ) ≥ {\rm Confidence}(de\Rightarrow a)\ge Confidence(de⇒a)≥ min_conf,所以强关联规则为
a d ⇒ e [ 0.4 , 1.0 ] d e ⇒ a [ 0.4 , 0.8 ] ad\Rightarrow e \;\;\;\; [0.4, 1.0]\\ de \Rightarrow a \;\;\;\; [0.4,0.8] ad⇒e[0.4,1.0]de⇒a[0.4,0.8]
2. 基于表 1 1 1 回答下列问题(min_sup=40%):
-
使用 FP-Growth 算法确定频繁项集、FP 树和条件模式基。
根据 C1,可以统计出 F - l i s t = e , a , b , d , c {\rm F\text-list} = e, a, b, d, c F-list=e,a,b,d,c。根据 F - l i s t \rm F\text-list F-list,对表 1 1 1 进行筛选、排序,得到表 2 2 2。
Transaction ID Items Bought 0001 {e, a, d} 0024 {e, a, b, c} 0012 {e, a, b, d} 0031 {e, a, d, c} 0015 {e, b, c} 0022 {e, b, d} 0029 {d, c} 0040 {a, b, c} 0033 {e, a, d} 0038 {e, a, b}
表 2 经过过滤、排序后的数据
构建的 FP 树如图 2 2 2 所示。

图 2 FP 树
从出现频次少的 item 开始确定条件模式基、条件 FP 树和频繁项集。
c 的条件模式基为 {{e,a,b:1}, {e,a,d:1}, {e,b:1}, {d:1}, {a,b:1}},统计基于其条件模式基的候选一项集:{a:3,b:3,e:3,d:2}。由于均小于最小支持度,所以不存在(条件)频繁一项集,无法构建条件 FP 树,也没法构建频繁二项集。
d 的条件模式基为 {{e,a,b:1}, {e,a:3}, {e,b:1}},统计候选一项集:{e:5, a:4, b:2}。只有 b 小于最小支持度,所以频繁一项集为 {e:5, a:4}。现在,以 d 的条件模式基作为”数据集“,执行构建 FP 树的过程,即按照频次对一项集排序,去掉数据集中每条数据的非频繁项并排序,最后基于处理后的数据集构建 FP 树,该树为 d 的条件 FP 树,如图 3 3 3 所示。

图 3 d-conditional FP tree
由于该 FP 树只有一条路径,因此无需递归建树,根据 d 对应的条件 FP 树统计的频繁项集为 {ead:4, ed:5, ad:4}。在表 2 2 2 所示的原始数据集中进行验证,结果正确。
b 的条件模式基为 {{e,a:3}, {e:2}, {a:1}},频繁一项集为 {e:5, a:4}。条件 FP 树如图 4 4 4 所示。

图 4 b-conditional FP tree
统计频繁二项集为 {eb:5, ab:4}。由于不止一条路径,所以统计频繁三项集需要递归建树。建立 ba 条件 FP 树,需要从图 4 4 4 中确定 a 的条件模式基 {{e:3}},以该条件模式基为”数据集“,统计频繁一项集发现为空,所以无法建立 ba 条件 FP 树,故无法生成频繁三项集。再建立 be 条件 FP 树,显然,其条件模式基为空,建树与生成频繁项集也无从谈起。
a 的条件模式基为 {{e:6}},频繁一项集为 {e:6}。条件 FP 树如图 5 5 5 所示,由此确定频繁项集为 {ea:6}。

图 5 a-conditional FP tree
e 的条件模式基为空,所以不考虑。
综上所述,根据 FP-Growth 算法确定的频繁项集为 {a},{b},{c},{d},{e},{ab},{ad},{ae},{be},{de},{ade}。与 Apriori 算法结果一致。
-
对比 FP-Growth 和 Apriori 的效率。
FP-Growth 算法只需要对数据集遍历两次,所以速度更快。FP 树将集合按照支持度降序排序,不同路径如果有相同前缀路径共用存储空间,使得数据得到了压缩。相比于 Apriori,FP 树第二次遍历会存储很多中间过程的值,会占用很多内存。
3. 使用 AGNES 算法将表 4 4 4 所示的十个点聚类成两类。
| ID | Name | Pos |
| 0 | A1 | (4,2,5) |
| 1 | A2 | (10,5,2) |
| 2 | A3 | (5,8,7) |
| 3 | B1 | (1,1,1) |
| 4 | B2 | (2,3,2) |
| 5 | B3 | (3,6,9) |
| 6 | C1 | (11,9,2) |
| 7 | C2 | (1,4,6) |
| 8 | C3 | (9,1,7) |
| 9 | C4 | (5,6,7) |
表 4 十点位置
① 合并 A3 和 C4,二者的欧式距离为 2 2 2,记簇为 α \alpha α。
② 合并 B1 和 B2,二者距离为 6 \sqrt 6 6,记簇为 β \beta β;
③ 合并 B3 和 α \alpha α,二者距离由 B3 与 α \alpha α 中最近点的距离定义,即 B3 与 C4,距离为 8 \sqrt 8 8,记簇为 α \alpha α;
④ 合并 β \beta β、A1 和 C2, β \beta β 与 A1 的距离定义为 C2 与 A1 的距离,即 14 \sqrt {14} 14,B2 与 A1 的距离也为 14 \sqrt{ 14} 14,所以三者合并,记簇为 β \beta β;
⑤ 合并 A2 和 C1,二者距离为 17 \sqrt {17} 17。另外,合并 α \alpha α 和 β \beta β,二者距离由 B3 和 C2 决定,也为 17 \sqrt{17} 17。分别记簇为 γ \gamma γ 和 α \alpha α;
⑥ 合并 C3 和 α \alpha α,二者距离由 C3 和 A1 决定,即 30 \sqrt{30} 30,记簇为 α \alpha α。
此时只剩两个簇, α \alpha α 和 γ \gamma γ,分别为 {A2, C1} 和 {A1, A3, B1, B2, B3, C2, C3, C4}。
通过程序代码验证,如图 6 6 6 所示。

图 6 分类前(左)、分类过程(中)和分类后(右)
对应代码如下:
#步骤1:创建数据
import matplotlib.pyplot as plt
import numpy as np
X = np.array([[4,2,5], [10,5,2], [5,8,7], [1,1,1], [2,3,2], [3,6,9], [11,9,2], [1,4,6], [9,1,7], [5,6,7]])
fig = plt.figure(figsize=(8, 5))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c='b')
plt.show()
#步骤 2:调用函数实现层次聚类
from scipy.cluster.hierarchy import linkage
Z = linkage(X, method='single', metric='euclidean')
#步骤 3:画出树形图
from scipy.cluster.hierarchy import dendrogram
plt.figure(figsize=(8, 5))
dendrogram(Z,p=1, leaf_font_size=10)
plt.show()
#步骤 4:获取聚类结果
from scipy.cluster.hierarchy import fcluster
# 根据聚类数目返回聚类结果
k = 2
labels_2 = fcluster(Z, t=k, criterion='maxclust')
# 聚类的结果可视化,相同的类的样本点用同一种颜色表示
fig = plt.figure(figsize=(8, 5))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=labels_2, cmap='prism')
plt.show()
4. 根据表 5 5 5 所示的 User-Product rating 矩阵回答下列问题:
| Product 1 | Product 2 | Product 3 | Product 4 | |
| User 1 | 1 | 1 | 5 | 3 |
| User 2 | 3 | ? | 5 | 4 |
| User 3 | 1 | 3 | 1 | 1 |
| User 4 | 4 | 3 | 2 | 1 |
| User 5 | 2 | 2 | 2 | 4 |
表 5 User-Product
-
使用余弦相似度计算与 User 2 最相似的三个 User。
s i m ( 1 , 2 ) = 1 × 3 + 5 × 5 + 3 × 4 35 50 ≈ 0.956 s i m ( 3 , 2 ) = 1 × 3 + 1 × 5 + 1 × 4 3 50 ≈ 0.980 s i m ( 4 , 2 ) = 4 × 3 + 2 × 5 + 1 × 4 21 50 ≈ 0.802 s i m ( 5 , 2 ) = 2 × 3 + 2 × 5 + 4 × 4 24 50 ≈ 0.924 \begin{align} {\rm sim}(1,2) = \frac{1\times 3 + 5\times 5 + 3\times 4}{\sqrt{35} \sqrt{50}} ≈ 0.956 \\ {\rm sim}(3,2) = \frac{1\times 3 + 1\times 5 + 1\times 4}{\sqrt{3} \sqrt{50}} ≈ 0.980 \\ {\rm sim}(4,2) = \frac{4\times 3 + 2\times 5 + 1\times 4}{\sqrt{21} \sqrt{50}} ≈ 0.802 \\ {\rm sim}(5,2) = \frac{2\times 3 + 2\times 5 + 4\times 4}{\sqrt{24} \sqrt{50}} ≈ 0.924 \\ \end{align} sim(1,2)=35501×3+5×5+3×4≈0.956sim(3,2)=3501×3+1×5+1×4≈0.980sim(4,2)=21504×3+2×5+1×4≈0.802sim(5,2)=24502×3+2×5+4×4≈0.924
显然,User 2 和 User 1、User 3、User 5 最相似。 -
使用与 User 2 最相似的三个 User 预测 User 2 的 Product 2。
r ˉ U s e r 1 = 1 4 ( 1 + 1 + 5 + 3 ) = 5 2 r ˉ U s e r 2 = 1 3 ( 3 + 5 + 3 ) = 4 r ˉ U s e r 3 = 1 4 ( 1 + 3 + 1 + 1 ) = 3 2 r ˉ U s e r 5 = 1 4 ( 2 + 2 + 2 + 4 ) = 5 2 \begin{align} \bar r_{\rm User \;1} &= \frac{1}{4}(1+1+5+3) = \frac{5}{2} \\ \bar r_{\rm User \;2} &= \frac{1}{3} (3+5+3) = 4 \\ \bar r_{\rm User \;3} &= \frac{1}{4} (1+3+1+1) = \frac{3}{2} \\ \bar r_{\rm User \;5} &= \frac{1}{4}(2+2+2+4) = \frac{5}{2} \end{align} rˉUser1rˉUser2rˉUser3rˉUser5=41(1+1+5+3)=25=31(3+5+3)=4=41(1+3+1+1)=23=41(2+2+2+4)=25r U s e r 2 , P r o d u c t 2 = r ˉ U s e r 2 + s i m ( 1 , 2 ) ( r U s e r 1 , P r o d u c t 2 − r ˉ U s e r 1 ) + s i m ( 3 , 2 ) ( r U s e r 3 , P r o d u c t 2 − r ˉ U s e r 3 ) + s i m ( 5 , 2 ) ( r U s e r 5 , P r o d u c t 2 − r ˉ U s e r 5 ) s i m ( 1 , 2 ) + s i m ( 3 , 2 ) + s i m ( 5 , 2 ) ≈ 3.851 \begin{align} r_{\rm User \;2, Product \;2} &= \bar r_{\rm User \;2} + \frac{{{\rm sim(1,2)}(r_{\rm User\; 1, Product\;2}- \bar r_{\rm User\; 1}) } + {{\rm sim(3,2)}(r_{\rm User\; 3, Product\;2}- \bar r_{\rm User\; 3})} + {{\rm sim(5,2)}(r_{\rm User\; 5, Product\;2}- \bar r_{\rm User\; 5}) }}{\rm sim(1,2) + sim(3,2)+ sim(5,2)} \\ &≈ 3.851 \end{align} rUser2,Product2=rˉUser2+sim(1,2)+sim(3,2)+sim(5,2)sim(1,2)(rUser1,Product2−rˉUser1)+sim(3,2)(rUser3,Product2−rˉUser3)+sim(5,2)(rUser5,Product2−rˉUser5)≈3.851
Lab Part
Churn Management
churn_training.txt 文件包括 2000 条数据,churn_validation.txt 包括 1033 条数据。
-
采用决策树模型,设置 minimum records per child branch 为 40,pruning severity 为 70。

图 7 决策树
-
采用神经网络模型,默认设置。

图 8 神经网络
-
采用逻辑回归模型,默认设置。

图 9 逻辑回归
-
对比不同参数设置下的决策树模型、神经网络模型和逻辑回归模型。

图 10 不同参数下决策树的效果

图 11 不同参数下决策树的效果(续)

图 12 不同参数下神经网络的效果

图 13 不同参数下逻辑回归的效果
Market Basket Analysis
采用 Apriori 算法,设置 Minimum antecedent support 为 7%,Minimum confidence 为 45%,Maximum number of antecedents 为 4。
-
确定产生的关联规则。
全部关联规则如图 14 14 14 所示。

图 14 全部关联规则
-
分别按照提升度(lift)、支持度(support)和置信度(confidence)对关联规则进行排序,选择前五个非冗余的关联规则。
前五个关联规则如表 6 6 6 所示。
order lift support confidence 1 tomato souce → pasta pasta → milk biscuits, pasta → milk 2 coffee, milk → pasta water → milk water, pasta → milk 3 biscuits, pasta → milk biscuits → milk juices → milk 4 water, pasta → milk brioches → milk tomato souce → pasta 5 juices → milk yoghurt → milk yoghurt → milk 表 6 前五关联规则
比较符合常识,比如买番茄酱的购物者很可能意大利面;买意大利面的购物者很可能因为口渴买牛奶;买水或者酸奶等饮品的购物者常常会一起买上牛奶。
相关文章:

【数据挖掘】国科大刘莹老师数据挖掘课程作业 —— 第三次作业
Written Part 1. 基于表 1 1 1 回答下列问题(min_sup40%, min_conf75%): Transaction IDItems Bought0001{a, d, e}0024{a, b, c, e}0012{a, b, d, e}0031{a, c, d, e}0015{b, c, e}0022{b, d, e}0029{c, d}0040{a, b, c}0033{a, d, e}0038…...

Windows挂载NFS
ubuntu开启nfs 安装 sudo apt install nfs-kernel-server编辑 /etc/exports /data/share *(rw,no_root_squash)重启服务 sudo systemctl restart nfs-server.service验证 showmount -e localhostwindows连接NFS 选择控制面板 > 程序 > 启用或关闭 Windows 功能 添加…...
数据结构第五课 -----二叉树的代码实现
作者前言 🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂 🎂 作者介绍: 🎂🎂 🎂 🎉🎉🎉…...
工程师)
优橙内推北京专场——5G网络优化(中高级)工程师
可加入就业QQ群:801549240 联系老师内推简历投递邮箱:hrictyc.com 内推公司1:西安长河通讯有限责任公司 内推公司2:北京电旗通讯技术股份有限公司 内推公司3:润建股份有限公司 西安长河通讯有限责任公司 西安长河…...
Mysql DDL语句建表及空字符串查询出0问题
DDL语句建表 语法: create table 指定要建立库的库名.新建表名 (... 新建表的字段以及类型等 ...)comment 表的作用注释 charset 表编译格式 row_format DYNAMIC create table dev_dxtiot.sys_url_permission (id integer …...

深入ArkTS:应用状态管理与LocalStorage装饰器详解【鸿蒙专栏-11】
文章目录 ArkTS 应用状态管理详解LocalStorage: 页面级 UI 状态存储使用规则概述:装饰器详解:限制条件:使用场景:1. 应用逻辑使用 LocalStorage2. 从 UI 内部使用 LocalStorageArkTS 应用状态管理进阶LocalStorage 装饰器详解1. @LocalStorageProp2. @LocalStorageLink观察…...

管理Android12系统的WLAN热点
大家好!我是编码小哥,欢迎关注,持续分享更多实用的编程经验和开发技巧,共同进步。 要创建一个APK管理Android 12系统的WLAN热点,你需要遵循以下步骤: 1. 获取必要的权限和API访问权限。在AndroidManifest.xml文件中添加以下权限: ```xml <uses-permission android:…...

从0开始学习JavaScript--JavaScript 中 `let` 和 `const` 的区别及最佳实践
在JavaScript中,let 和 const 是两个用于声明变量的关键字。尽管它们看起来很相似,但它们之间有一些重要的区别。本篇博客将深入探讨 let 和 const 的用法、区别,并提供一些最佳实践,以确保在代码中正确使用它们。 let 和 const …...
【上海大学数字逻辑实验报告】二、组合电路(一)
一、 实验目的 熟悉TTL异或门构成逻辑电路的基本方式;熟悉组合电路的分析方法,测试组合逻辑电路的功能;掌握构造半加器和全加器的逻辑测试;学习使用可编程逻辑器件的开发工具 Quartus II设计电路。 二、 实验原理 异或门是数字…...

lodash中foreach踩坑
什么是lodash Lodash 是一个 JavaScript 实用工具库,提供了很多用于处理数据、简化开发等方面的功能。它提供了一组常用的工具函数,用于处理数组、对象、字符串等常见数据结构,同时也包含了一些函数式编程的工具。对于前端开发来说ÿ…...
Unity C++交互
一、设置Dll输出。 两种方式: 第一:直接创建动态链接库工程第二:创建的是可执行程序,在visual studio,右键项目->属性(由exe改成dll) 二、生成Dll 根据选项Release或Debug,运行完上面的生成解决方案后…...
人工智能-优化算法之动量法
对于嘈杂的梯度,我们在选择学习率需要格外谨慎。 如果衰减速度太快,收敛就会停滞。 相反,如果太宽松,我们可能无法收敛到最优解。 泄漏平均值 小批量随机梯度下降作为加速计算的手段。 它也有很好的副作用,即平均梯度…...

【MySQL】InnoDB中的索引
目录标题 索引底层的数据结构:B树B树与B树的区别InnoDB与MyISAM在B树使用索引结构的不同? 聚簇索引非聚簇索引联合索引 B树索引适用的条件查询全值匹配匹配左边的列匹配列前缀匹配范围的值精确匹配某一列并范围匹配另外一列避免使用隐式转换 排序必须按照…...
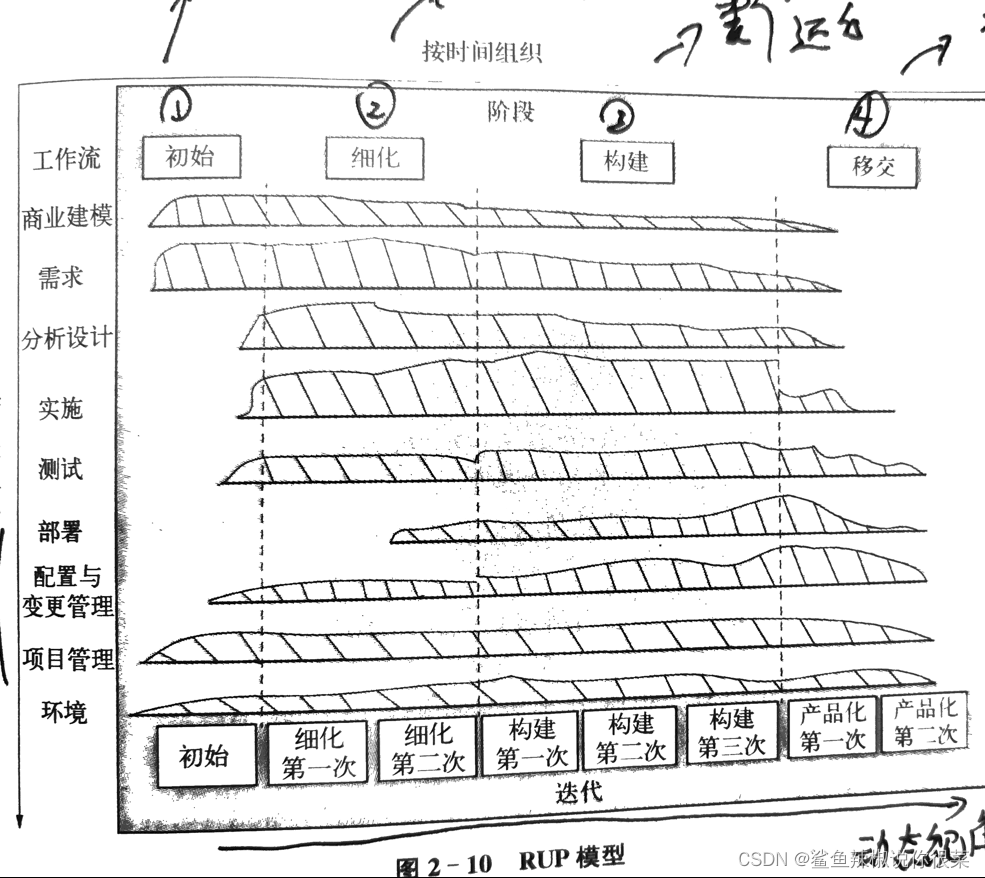
《软件工程原理与实践》复习总结与习题——软件工程
软件生命周期 软件生命周期分为三个时期、八个阶段 软件定义时期: 1)问题定义阶段:要解决什么问题 2)可行性研究阶段:确定软件开发可行 3)需求分析阶段:系统做什么 软件开发时期:…...

软工2021上下午第六题(组合模式)
阅读下列说明和Java代码,将应填入(n)处的字句写在答题纸的对应栏内。 【说明】 层叠菜单是窗口风格的软件系统中经常采用的一种系统功能组织方式。层叠菜单中包含的可能是一个菜单项(直接对应某个功能),也可…...

在Spring Boot中使用不同的日志
前言,本篇就是介绍在Java中使用相关的日志,适合初学者看,如果对这篇不感兴趣的可以移步了,本篇主要围绕我们Java中的几种日志类型,也说不上有多深入,算的上浅入浅出吧,如果你有一段时间的开发经…...

运维知识点-openResty
openResty 企业级实战——畅购商城SpringCloud-网站首页高可用解决方案-openRestynginxlua——实现广告缓存测试企业级实战——畅购商城SpringCloud-网站首页高可用解决方案-openRestynginxlua——OpenResty 企业级实战——畅购商城SpringCloud-网站首页高可用解决方案-openRes…...
微服务中配置Nacos热更新
启动Nacos startup.cmd -m standalone 在IDE中启动服务 打开nacos管理后台并选择配置列表 创建配置(这里以日期格式为例) 因为这里配置的是userservice的服务,所以在userservice服务的pom文件中引入依赖 配置一个bootstrap.yml文件 注意这里bootstrap文件中配置过的内容,在app…...
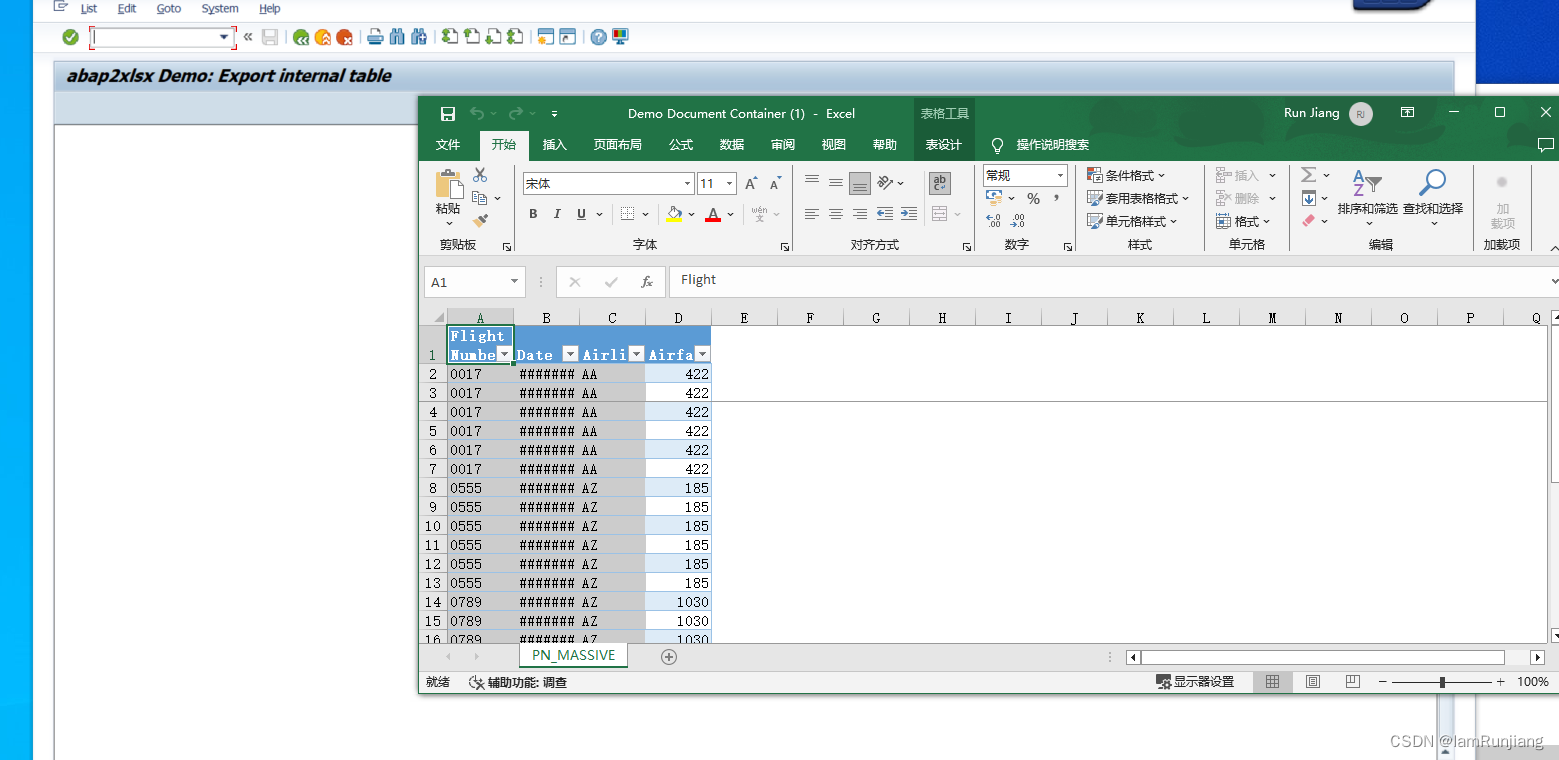
ABAP2XLSX 的安装和demo
ABAP2XLSX 是一个git上面的很好用的工具,它可以帮助abaper们更方便,更简单的生成各种各样复杂的自定义的excel,以满足各企业的信息化建设 在安装这个之前,请先查看之前的博客,去安装abapgit abap2xlsx地址࿱…...
记一篇Centos7安装innodb_ruby
安装innodb_ruby过程非常坎坷,这里记录下安装过程,有些坑当时没有记录下来,主要把完成安装过程就记录下来 yum安装ruby默认的会安装ruby2.0.0版本,但是在安装innodb_ruby时,会报错,提示至少需要2.4版本以上…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...
