图面试专题
一、概念
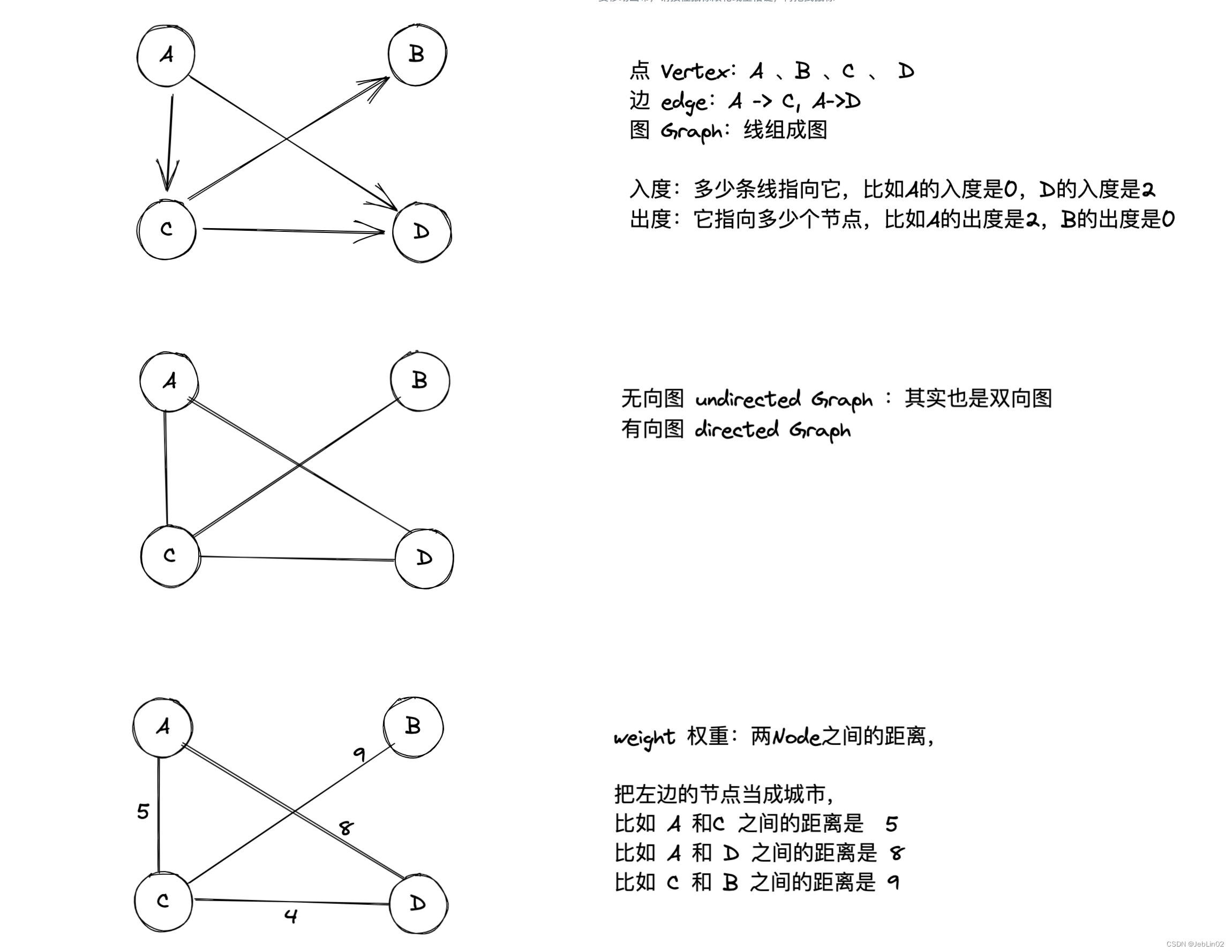
和二叉树的区别:图可能有环
常见概念
- 顶点(Vertex): 图中的节点或点。
- 边(Edge): 顶点之间的连接线,描述节点之间的关系。
- 有向图(Directed Graph): 边具有方向性的图,边有箭头表示方向。
- 无向图(Undirected Graph): 边没有方向性的图。
- 路径(Path): 顶点序列,通过边连接的顶点序列。
- 回路(Cycle): 闭合的路径,起点和终点相同的路径。
- 连通图(Connected Graph): 图中任意两个顶点之间都存在路径的图。
- 强连通图(Strongly Connected Graph): 有向图中任意两个顶点之间都存在双向路径的图。
- 连通分量(Connected Component): 无向图中的极大连通子图。
- 树(Tree): 无环连通图,任意两个节点都有唯一路径。
- 森林(Forest): 多个不相交树的集合。
- 度(Degree): 顶点的度是指与该顶点相关联的边的数量。
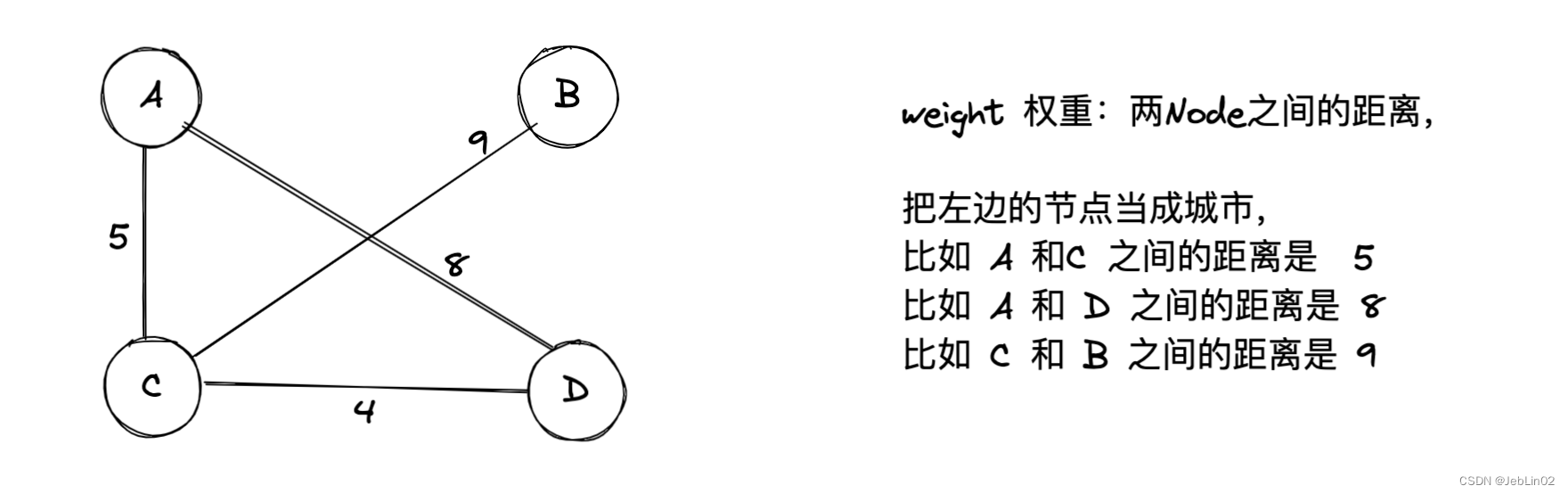
- 权重(Weight): 边或者顶点上的数值,表示边的代价或者顶点的属性。
邻接矩阵
| A | B | C | D | |
| A | 0 | 正无穷 | 5 | 8 |
| B | 正无穷 | 0 | 9 | 正无穷 |
| C | 5 | 9 | 0 | 4 |
| D | 8 | 正无穷 | 4 | 0 |
邻接表法
| Node | weight | |
| A | C | 5 |
| A | D | 8 |
| C | B | 9 |
| C | D | 4 |
| B | C | 9 |
| D | A | 8 |
| D | C | 4 |
二、算法题
1、套路模板
/*** @author jeb_lin* 22:27 2023/11/29*/
public class Node {public int value; // 可以改成 Stringpublic int in;// 入度public int out;// 出度public ArrayList<Node> nexts; // 多个后继节点public ArrayList<Edge> edges; // 多条边,该节点指出去的public Node(int value){this.value = value;this.in = 0;this.out = 0;this.nexts = new ArrayList<>();this.edges = new ArrayList<>();}public int getValue() {return value;}public void setValue(int value) {this.value = value;}public int getIn() {return in;}public void setIn(int in) {this.in = in;}public int getOut() {return out;}public void setOut(int out) {this.out = out;}public ArrayList<Node> getNexts() {return nexts;}public void setNexts(ArrayList<Node> nexts) {this.nexts = nexts;}public ArrayList<Edge> getEdges() {return edges;}public void setEdges(ArrayList<Edge> edges) {this.edges = edges;}
}
/*** @author jeb_lin* 22:27 2023/11/29*/
public class Edge {public Node from;public Node to;public int weight;public Edge(Node from, Node to, int weight) {this.weight = weight;this.from = from;this.to = to;}// 复写下面这俩,是为了放入Set的时候能正确去重@Overridepublic boolean equals(Object obj) {if (this == obj) {return true;}if (obj == null || !(obj instanceof Edge)) {return false;}Edge edge = (Edge) obj;return this.weight == edge.weight && Objects.equals(edge.from, this.from) && Objects.equals(edge.to, this.to);}@Overridepublic int hashCode() {return this.weight * this.from.hashCode() * this.to.hashCode();}public Node getFrom() {return from;}public void setFrom(Node from) {this.from = from;}public Node getTo() {return to;}public void setTo(Node to) {this.to = to;}public int getWeight() {return weight;}public void setWeight(int weight) {this.weight = weight;}
}
/*** @author jeb_lin* 22:26 2023/11/29*/
public class Graph {public HashMap<Integer,Node> nodes; // 该图上面的所有Node,nodeVal -> Nodepublic HashSet<Edge> edges; // 该图上面的所有边public Graph(){this.nodes = new HashMap<>();this.edges = new HashSet<>();}public HashMap<Integer, Node> getNodes() {return nodes;}public void setNodes(HashMap<Integer, Node> nodes) {this.nodes = nodes;}public HashSet<Edge> getEdges() {return edges;}public void setEdges(HashSet<Edge> edges) {this.edges = edges;}
}
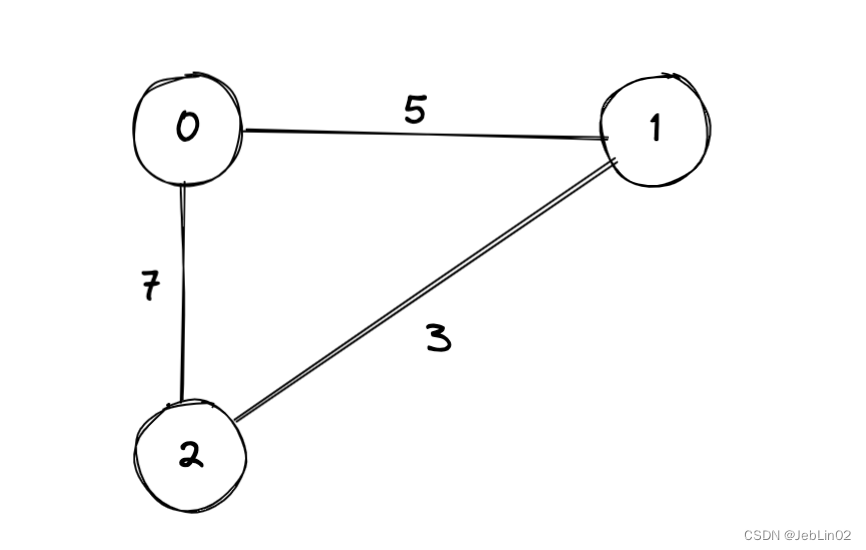
2、二维数组转化成图
| 0 | 1 | 2 | 备注 | |
| 0 | 0 | 1 | 5 | Node0->Node1 ,weight=5 |
| 1 | 1 | 2 | 3 | Node1->Node2 ,weight=3 |
| 2 | 0 | 2 | 7 | Node0->Node2 ,weight=7 |
/*** 把二维数组转换成图* [* [0,1,5], // 表示 node0 -> node1 ,weight = 5* [1,2,3],* [0,2,7]* ]** @param matrix* @return*/public static Graph createGraph(int[][] matrix) {Graph graph = new Graph();HashMap<Integer, Node> nodes = new HashMap<>(); // 该图上面的所有Node,nodeVal -> NodeHashSet<Edge> edges = new HashSet<>(); // 该图上面的所有边graph.setEdges(edges);graph.setNodes(nodes);for (int i = 0; i < matrix.length; i++) {int[] row = matrix[i];if (!nodes.containsKey(row[0])) {nodes.put(row[0], new Node(row[0]));}if (!nodes.containsKey(row[1])) {nodes.put(row[1], new Node(row[1]));}Node from = nodes.get(row[0]);Node to = nodes.get(row[1]);from.setOut(from.getOut() + 1);to.setIn(to.getIn() + 1);from.getNexts().add(to);Edge edgeTemp = new Edge(from, to, row[2]);from.getEdges().add(edgeTemp);if(!edges.contains(edgeTemp)){edges.add(edgeTemp);}}return graph;}public static void main(String[] args) {int[][] arr = {{0, 1, 5}, {1, 2, 3}, {0, 2, 7}};Graph graph = createGraph(arr);System.out.println("ok");}相关文章:

图面试专题
一、概念 和二叉树的区别:图可能有环 常见概念 顶点(Vertex): 图中的节点或点。边(Edge): 顶点之间的连接线,描述节点之间的关系。有向图(Directed Graph)&…...

VUE的计算属性
<!DOCTYPE html> <html> <head> <meta charset"UTF-8" /> <title>计算属性</title> </head> <style> table { border: 1px solid #000; text-align: center; width: 240px; } th,td { border: 1px solid #000; …...

uniapp中使用pageScrollTo让页面滚动到固定节点或距离
uniapp中使用pageScrollTo让页面滚动到固定节点或距离 思路:计算当前节点距离顶部的距离滚动距离然后使用pageScrollTo进行滚动(要保证页面加载完成之后在执行) #topic" id :页面的节点 changeTop(id) {let query uni.c…...

使用机器学习方法进行分析和处理:对高质量图像进行压缩
使用SVD(奇异值分解)进行图像压缩与普通压缩工具压缩的主要区别在于压缩原理和压缩效果。 压缩原理: 普通图像压缩工具通常采用有损压缩或无损压缩算法,如JPEG、PNG等,它们主要针对图像的像素进行变换和编码。而SVD图像…...

多线程面试总结
1. 创建线程有哪几种方式 创建线程有三种方式,分别是继承Thread类、实现Runnable接口、实现Callable接口。 通过继承Thread类来创建并启动线程的步骤如下: 定义Thread类的子类,并重写该类的run()方法,该run()方法将作为线程执行…...

android11-隐藏状态栏和导航栏
隐藏导航栏 /android11/frameworks/base/packages/SystemUI/res/layout/navigation_bar.xml diff --git a/frameworks/base/packages/SystemUI/res/layout/navigation_bar.xml b/frameworks/base/packages/SystemUI/res/layout/navigation_bar.xml index ba6b6956f1..6db2348…...
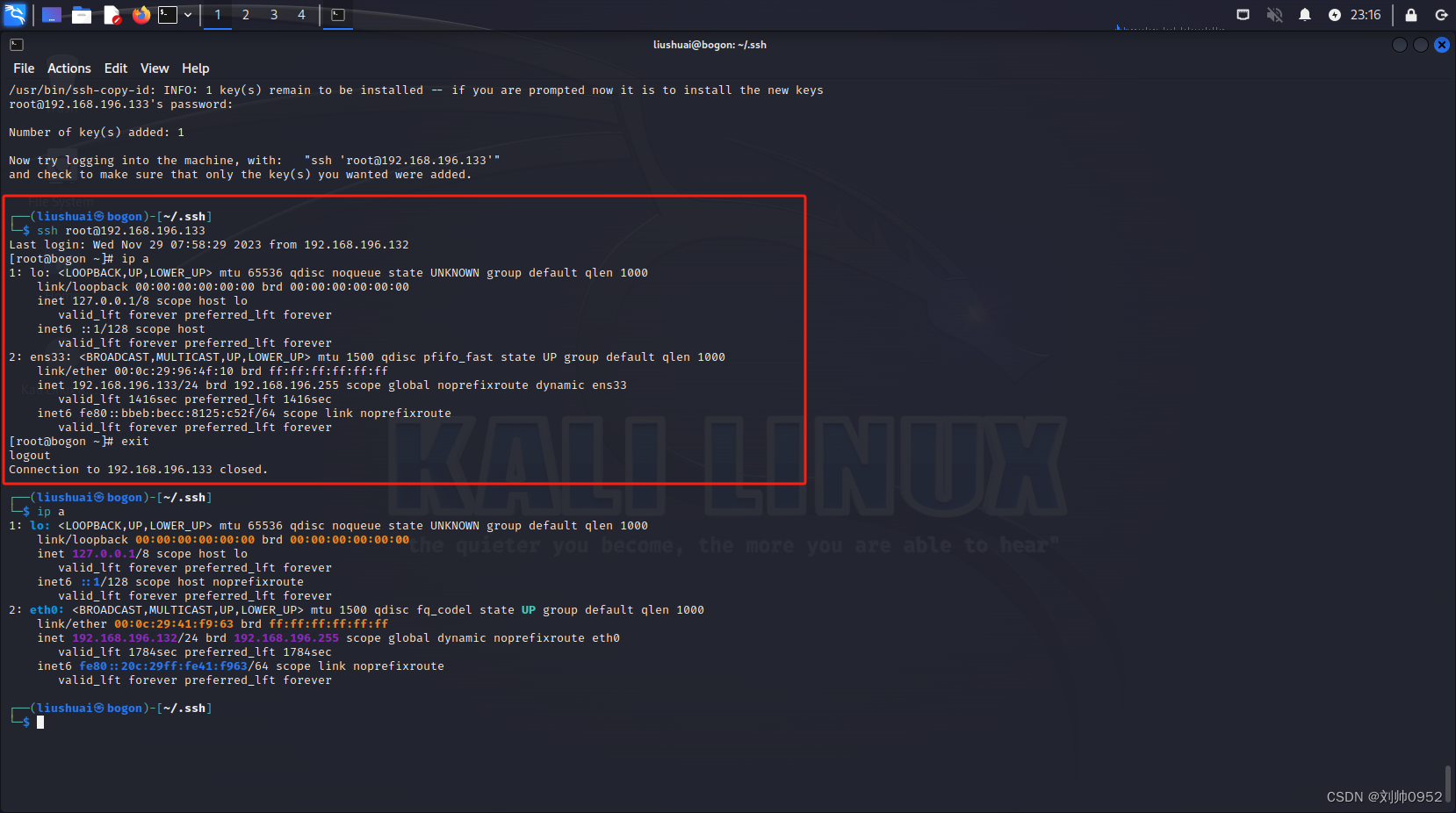
血的教训--kail系统免密centos7的坑【高版本ssh免密低版本ssh的坑】
血的教训–kail系统免密centos7的坑【高版本ssh免密低版本ssh的坑】 最近下载了一个2023版本的kail系统,但是经过几次设置免密后,ssh过去一直让提供密码,所以就仔细的分析了一下,果然还是发现了点猫腻 接上一个博客,大…...
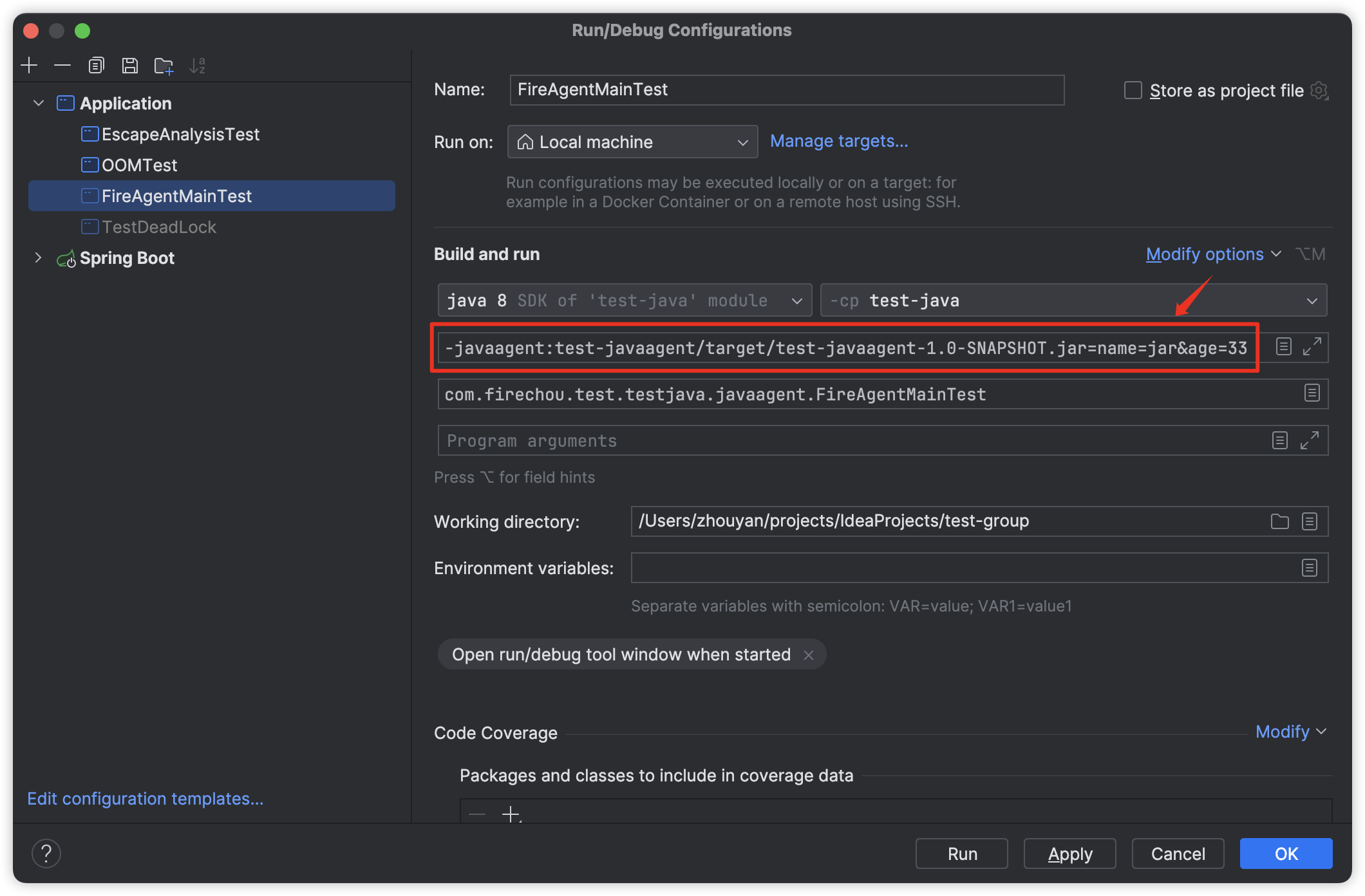
javaagent字节码增强浅尝
概述 javaagent 技术广泛应用于对代码的增强,比如统计方法执行时间、GC 信息打印、分布式链路跟踪等;实现方式包括 javassist 和 bytebuddy,bytebuddy 是对 javassist 的改进;类似于 spring 中的 AOP; Instrumentati…...
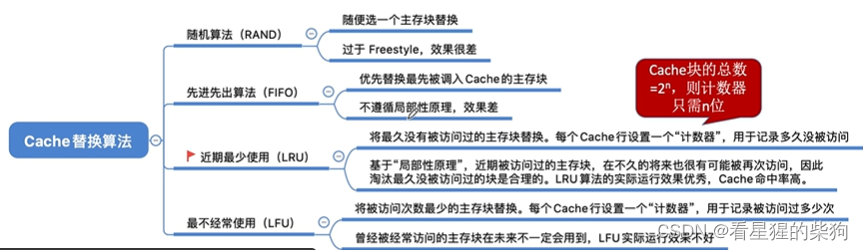
计算机组成原理-Cache替换算法
文章目录 总览随机算法(RAND)先进先出算法(FIFO)近期最少使用算法(LRU)最不经常使用算法(LFU)总结 总览 随机算法(RAND) 没有选择性地考虑替换哪一块Cache&a…...

Adobe 家族系列download
adobe 前言 Adobe公司的产品线中拥有多个家族桶,下面是Adobe全家桶产品的功能介绍: Creative Cloud(创意云):包含Photoshop、Illustrator、InDesign、Premiere Pro、After Effects、Lightroom等创意设计、视频制作和…...
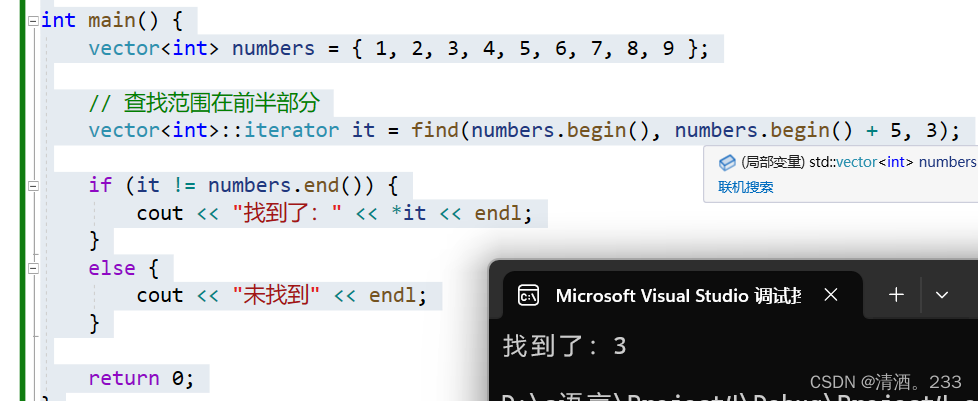
97.STL-查找算法 find
目录 STL-查找算法find 1.基本用法: 2.查找自定义类型: 3.查找范围: STL-查找算法find 在C的STL(标准模板库)中,find 算法用于在指定范围内查找指定值的元素。 功能描述: 查找指定元素&…...

如何应对雨天飞行的挑战?无人机机库防护能力解析
一、 背景介绍 无人机机库是无人机停放和起降场所,类似传统飞机的 hangar(飞机库)。它是一个专门用于存储、维护和保护无人机的设施。无人机机库的存在有助于提高无人机的安全性,同时也为无人机提供了一个有序的管理场所。 雨天…...

机器学习笔记 - 3D数据的常见表示方式
一、简述 从单一角度而自动合成3D数据是人类视觉和大脑的基本功能,这对计算机视觉算法来说是比较难的。但随着LiDAR、RGB-D 相机(RealSense、Kinect)和3D扫描仪等3D传感器的普及和价格的降低,3D 采集技术的最新进展取得了巨大飞跃。与广泛使用的 2D 数据不同,3D 数据具有丰…...
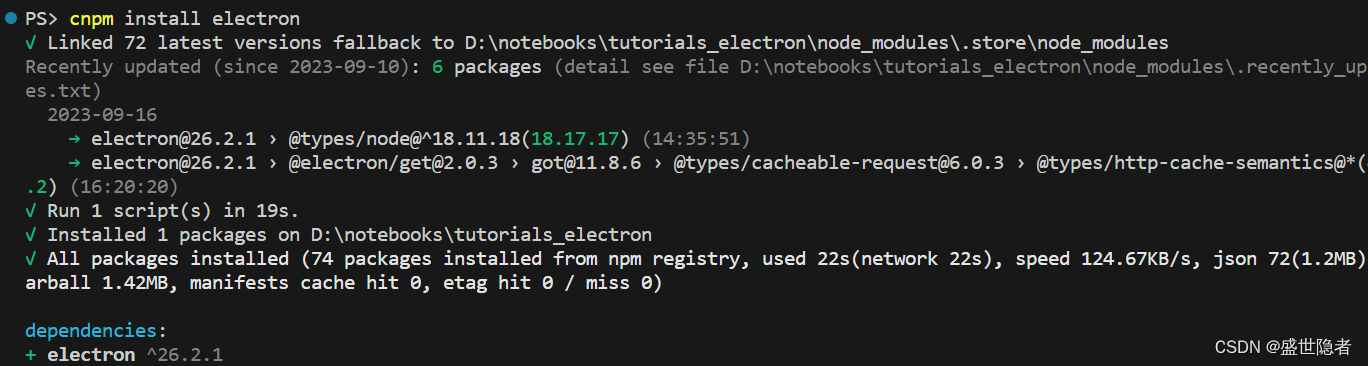
【Node.js】解决npm报错:RequestError: unable to verify the first certificate
1. 问题简述 帖主从nodejs官网下载安装nodejs后,发现使用以下命令安装electron会报错: npm install electron 报错信息如下: npm ERR! RequestError: unable to verify the first certificate 2. 解决方案 网上列举的方案,无…...
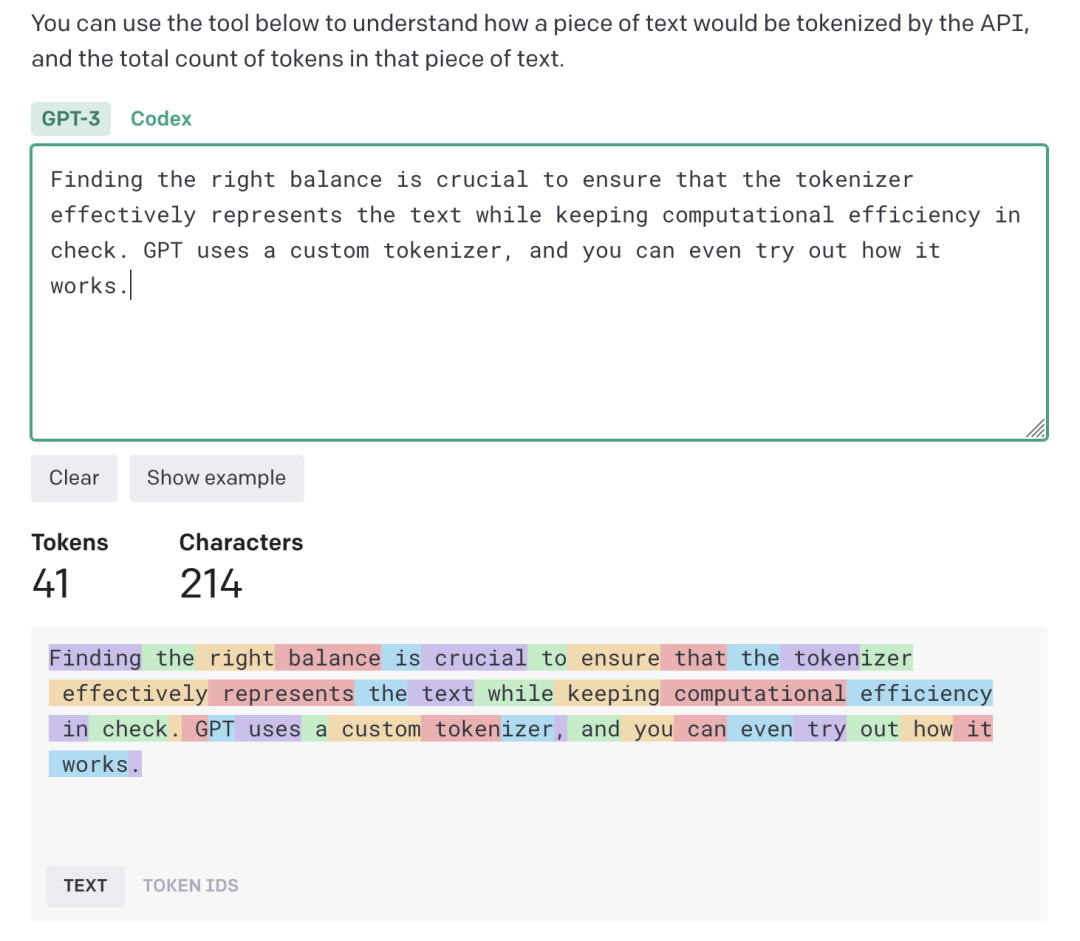
语言模型文本处理基石:Tokenizer简明概述
编者按:近年来,人工智能技术飞速发展,尤其是大型语言模型的问世,让 AI 写作、聊天等能力有了质的飞跃。如何更好地理解和利用这些生成式 AI,成为许多开发者和用户关心的问题。 今天,我们推出的这篇文章有助…...
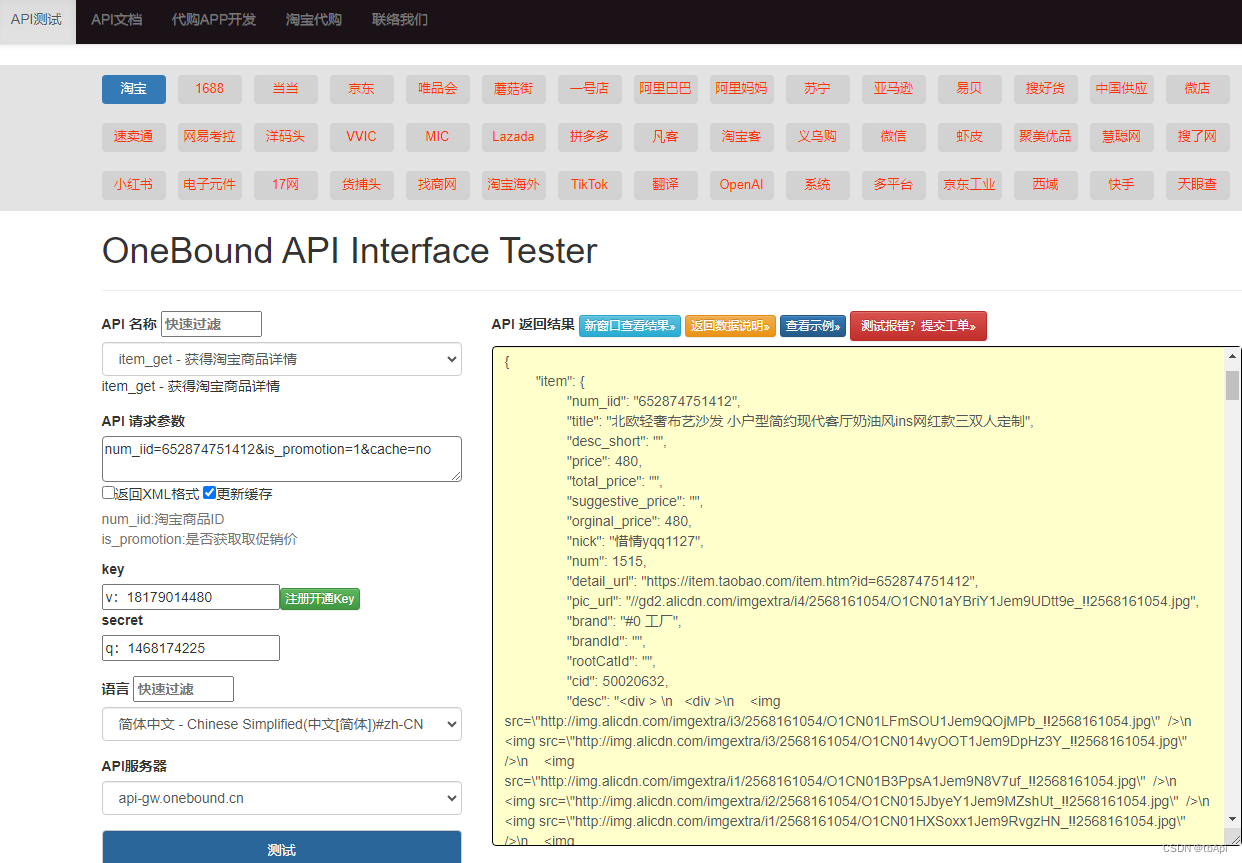
淘宝商品详情数据接口(店铺搬家、数据分析、代购商城、ERP选品、无货源铺货、品牌监控)
使用淘宝API接口需要以下步骤: 注册开发者账号:在淘宝开放平台(https://o0b.cn/anzexi)上注册一个开发者账号,并创建一个应用。 获取API密钥:在应用页面上获取API密钥,这是后续调用API接口的凭…...
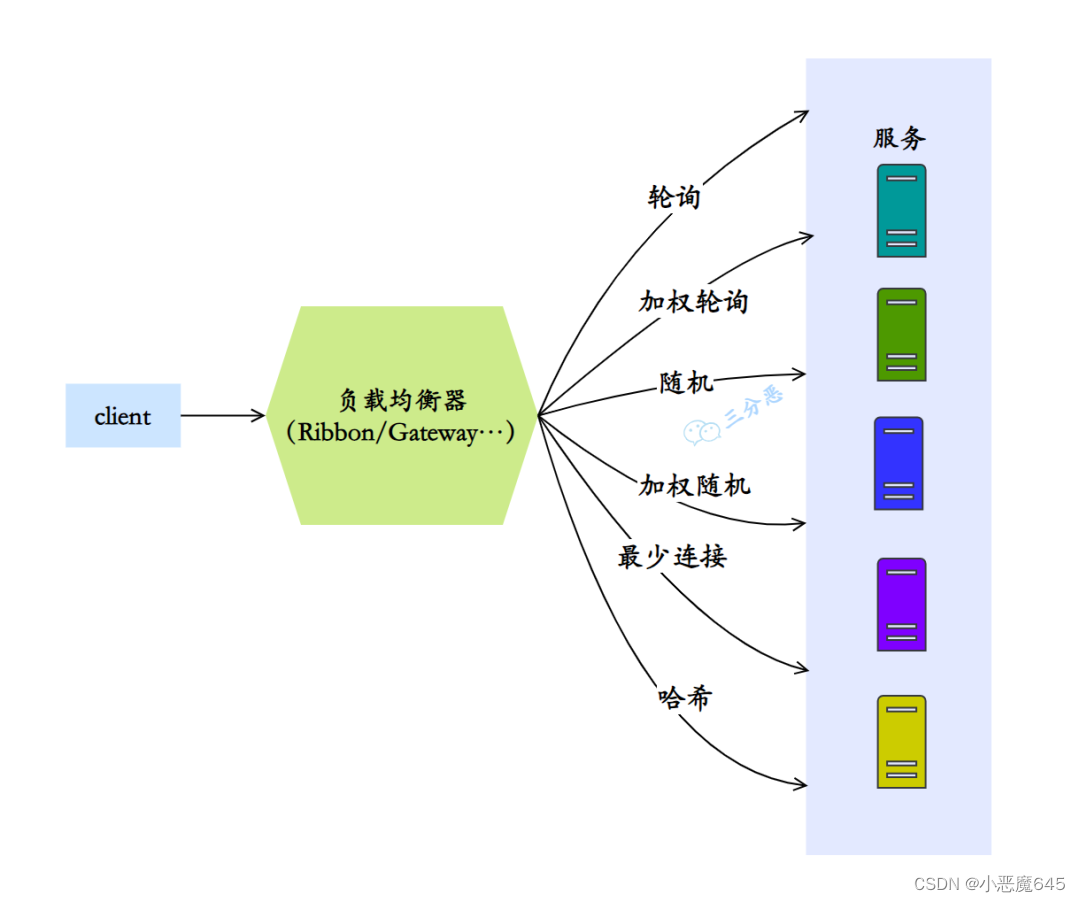
面试篇之微服务(一)
目录 概览 1.什么是微服务? 2.微服务带来了哪些挑战? 3.现在有哪些流行的微服务解决方案? 这三种方案有什么区别吗? 4.说下微服务有哪些组件? 注册中心 5.注册中心是用来干什么的? 6.SpringCloud可…...
智慧科研助力科研数据的分析处理
如今,科研领域的发展日新月异,数据量也越来越大。这时,智慧科研可视化技术不仅为科研人员提供了快速高效的数据分析手段,而且为科研工作的推进提供了新的思路和方法。通过可视化手段,我们可以将各种数据、信息、知识以…...

el-select实现分屏效果
动态绑定class值 ,多种判断 :class"type 8 ? home-stye-2 : type 24 ? home-stye-1 : home-stye-3" <div class"home-right-top"><div class"home-right-top-video"><el-row :gutter"20"><el-c…...
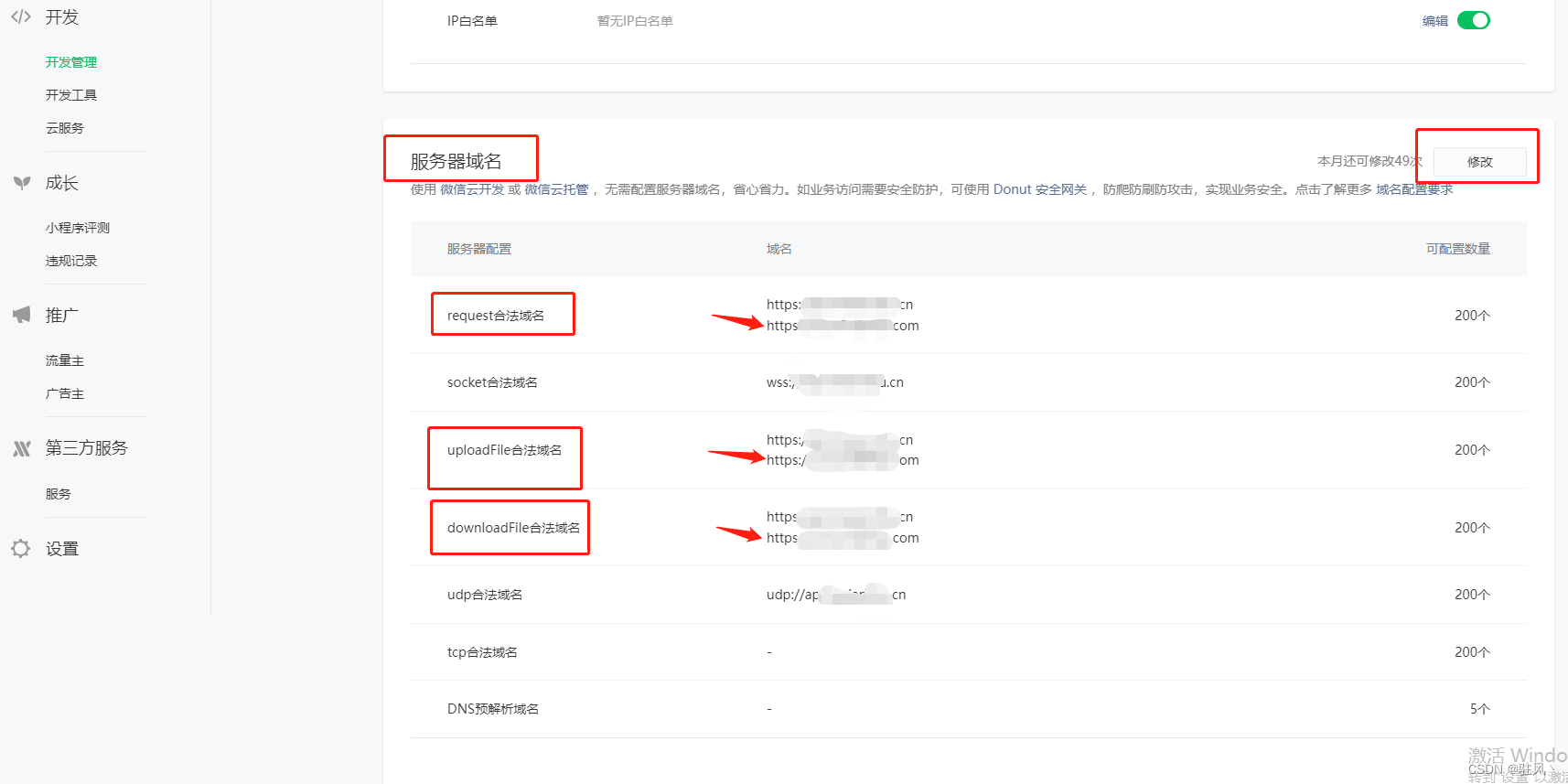
微信小程序本地和真机调试文件上传成功但体验版不成功
可能是微信小程序ip白名单的问题,去微信公众平台(小程序)上设置小程序的ip白名单 1、在本地中取消不校验 然后在本地去上传文件,就会发现控制台报错了,会提示一个https什么不在ip白名单,复制那个网址 2、…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...