《斯坦福数据挖掘教程·第三版》读书笔记(英文版)Chapter 3 Finding Similar Items
来源:《斯坦福数据挖掘教程·第三版》对应的公开英文书和PPT
It is therefore a pleasant surprise to learn of a family of techniques called locality-sensitive hashing, or LSH, that allows us to focus on pairs that are likely to be similar, without having to look at all pairs. Thus, it is possible that we can avoid the quadratic growth in computation time that is required by the naive algorithm. There is usually a downside to locality-sensitive hashing, due to the presence of false negatives, that is, pairs of items that are similar, yet are not included in the set of pairs that we examine, but by careful tuning we can reduce the fraction of false negatives by increasing the number of pairs we consider.
The general idea behind LSH is that we hash items using many different hash functions. These hash functions are not the conventional sort of hash functions. Rather, they are carefully designed to have the property that pairs are much more likely to wind up in the same bucket of a hash function if the items are similar than if they are not similar. We then can examine only the candidate pairs, which are pairs of items that wind up in the same bucket for at least one of the hash functions.
The Jaccard similarity of sets S and T is ∣ S ∩ T ∣ / ∣ S ∪ T ∣ |S ∩ T |/|S ∪ T | ∣S∩T∣/∣S∪T∣, that is, the ratio of the size of the intersection of S and T to the size of their union. We shall denote the Jaccard similarity of S and T by S I M ( S , T ) SIM(S, T ) SIM(S,T).
Shingling of Documents
A document is a string of characters. Define a k-shingle for a document to be any substring of length k found within the document. Then, we may associate with each document the set of k-shingles that appear one or more times within that document.
Suppose our document D is the string abcdabd, and we pick k = 2 k = 2 k=2. Then the set of 2-shingles for D is { a b , b c , c d , d a , b d } \{ab, bc, cd, da, bd\} {ab,bc,cd,da,bd}.
Note that the substring ab appears twice within D, but appears only once as a shingle. A variation of shingling produces a bag, rather than a set, so each shingle would appear in the result as many times as it appears in the document. However, we shall not use bags of shingles here.
k should be picked large enough that the probability of any given shingle appearing in any given document is low.
Instead of using substrings directly as shingles, we can pick a hash function that maps strings of length k to some number of buckets and treat the resulting bucket number as the shingle. The set representing a document is then the set of integers that are bucket numbers of one or more k-shingles that appear in the document. For instance, we could construct the set of 9-shingles for a document and then map each of those 9-shingles to a bucket number in the range 0 to 2 32 − 1 2^{32} − 1 232−1. Thus, each shingle is represented by four bytes instead of nine. Not only has the data been compacted, but we can now manipulate (hashed) shingles by single-word machine operations.
Our goal in this section is to replace large sets by much smaller representations called “signatures.” The important property we need for signatures is that we can compare the signatures of two sets and estimate the Jaccard similarity of the underlying sets from the signatures alone.
The signatures we desire to construct for sets are composed of the results of a large number of calculations, say several hundred, each of which is a “minhash” of the characteristic matrix.
To minhash a set represented by a column of the characteristic matrix, pick a permutation of the rows. The minhash value of any column is the number of the first row, in the permuted order, in which the column has a 1.
In this matrix, we can read off the values of h by scanning from the top until we come to a 1.
The probability that the minhash function for a random permutation of rows produces the same value for two sets equals the Jaccard similarity of those sets.
Call the minhash functions determined by these permutations h 1 , h 2 , . . . , h n h_1, h_2, . . . , h_n h1,h2,...,hn. From the column representing set S, construct the minhash signature for S, the
vector [ h 1 ( S ) , h 2 ( S ) , . . . , h n ( S ) ] [h_1(S), h_2(S), . . . , h_n(S)] [h1(S),h2(S),...,hn(S)]. We normally represent this list of hash-values as a column. Thus, we can form from matrix M a signature matrix, in which the ith column of M is replaced by the minhash signature for (the set of) the ith column.
Moreover, the more minhashings we use, i.e., the more rows in the signature matrix, the smaller the expected error in the estimate of the Jaccard similarity will be.
Fortunately, it is possible to simulate the effect of a random permutation by a random hash function that maps row numbers to as many buckets as there are rows. A hash function that maps integers 0 , 1 , . . . , k − 1 0, 1, . . . , k − 1 0,1,...,k−1 to bucket numbers 0 through k−1 typically will map some pairs of integers to the same bucket and leave other buckets unfilled.
However, the difference is unimportant as long as k is large and there are not too many collisions. We can maintain the fiction that our hash function h “permutes” row r to position h ( r ) h(r) h(r) in the permuted order.
Thus, instead of picking n random permutations of rows, we pick n randomly chosen hash functions h 1 , h 2 , . . . , h n h_1, h_2, . . . , h_n h1,h2,...,hn on the rows. We construct the signature matrix by considering each row in their given order. Let S I G ( i , c ) SIG(i, c) SIG(i,c) be the element of the signature matrix for the ith hash function and column c. Initially, set S I G ( i , c ) SIG(i, c) SIG(i,c) to ∞ for all i and c. We handle row r by doing the following:
- Compute h 1 ( r ) , h 2 ( r ) , . . . , h n ( r ) h_1(r), h_2(r), . . . , h_n(r) h1(r),h2(r),...,hn(r).
- For each column c do the following:
(a) If c has 0 in row r, do nothing.
(b) However, if c has 1 in row r, then for each i = 1 , 2 , . . . , n i = 1, 2, . . . , n i=1,2,...,n set S I G ( i , c ) SIG(i, c) SIG(i,c) to the smaller of the current value of S I G ( i , c ) SIG(i, c) SIG(i,c) and h i ( r ) h_i(r) hi(r).
Example


The process of minhashing is time-consuming, since we need to examine the entire k-row matrix M for each minhash function we want.
But to compute one minhash function on all the columns, we shall not go all the way to the end of the permutation, but only look at the first m out of k rows. If we make m small compared with k, we reduce the work by a large factor, k/m.
However, there is a downside to making m small. As long as each column has at least one 1 in the first m rows in permuted order, the rows after the mth have no effect on any minhash value and may as well not be looked at.
But what if some columns are all-0’s in the first m rows? We have no minhash value
for those columns, and will instead have to use a special symbol, for which we
shall use ∞.
When we examine the minhash signatures of two columns in order to estimate the Jaccard similarity of their underlying sets, we have to take into account the possibility that one or both columns have ∞ as their minhash value for some components of the signature. There are three cases:
- If neither column has ∞ in a given row, then there is no change needed. Count this row as an example of equal values if the two values are the same, and as an example of unequal values if not.
- One column has ∞ and the other does not. In this case, had we used all the rows of the original permuted matrix M, the column that has the ∞ would eventually have been given some row number, and that number will surely not be one of the first m rows in the permuted order. But the other column does have a value that is one of the first m rows. Thus, we surely have an example of unequal minhash values, and we count this row of the signature matrix as such an example.
- Suppose both columns have ∞ in row. Then in the original permuted matrix M, the first m rows of both columns were all 0’s. We thus have no information about the Jaccard similarity of the corresponding sets; that similarity is only a function of the last k − m k − m k−m rows, which we have chosen not to look at. We therefore count this row of the signature matrix as neither an example of equal values nor of unequal values.
As long as the third case, where both columns have ∞, is rare, we get almost as many examples to average as there are rows in the signature matrix. That effect will reduce the accuracy of our estimates of the Jaccard distance somewhat, but not much. And since we are now able to compute minhash values for all the columns much faster than if we examined all the rows of M, we can afford the time to apply a few more minhash functions. We get even better accuracy than originally, and we do so faster than before.
Suppose T is the set of elements of the universal set that are represented by the first m rows of matrix M. Let S 1 S_1 S1 and S 2 S_2 S2 be the sets represented by two columns of M. Then the first m rows of M represent the sets S1 ∩ T and S2 ∩ T . If both these sets are empty (i.e., both columns are all-0 in their first m rows), then this minhash function will be ∞ in both columns and will be ignored when estimating the Jaccard similarity of the columns’ underlying sets.
If at least one of the sets S1 ∩ T and S2 ∩ T is nonempty, then the probability of the two columns having equal values for this minhash function is the Jaccard similarity of these two sets, that is
∣ S 1 ∩ S 2 ∩ T ∣ ∣ ( S 1 ∪ S 2 ) ∩ T ∣ \frac{|S_1 ∩ S_2∩T|}{|(S_1\cup S_2)\cap T|} ∣(S1∪S2)∩T∣∣S1∩S2∩T∣
As long as T is chosen to be a random subset of the universal set, the expected value of this fraction will be the same as the Jaccard similarity of S 1 S_1 S1 and S 2 S_2 S2 However, there will be some random variation, since depending on T , we could find more or less than an average number of type X rows (1’s in both columns) and/or type Y rows (1 in one column and 0 in the other) among the first m rows of matrix M.
To mitigate this variation, we do not use the same set T for each minhashing that we do. Rather, we divide the rows of M into k / m k/m k/m groups. Then for each hash function, we compute one minhash value by examining only the first m rows of M, a different minhash value by examining only the second m rows, and so on. We thus get k / m k/m k/m minhash values from a single hash function and a single pass over all the rows of M. In fact, if k / m k/m k/m is large enough, we may get all the rows of the signature matrix that we need by a single hash function applied to each of the subsets of rows of M.
Locality-Sensitive Hashing for Documents
One general approach to LSH is to “hash” items several times, in such a way that similar items are more likely to be hashed to the same bucket than dissimilar items are. We then consider any pair that hashed to the same bucket for any of the hashings to be a candidate pair. We check only the candidate pairs for similarity. The hope is that most of the dissimilar pairs will never hash to the same bucket, and therefore will never be checked. Those dissimilar pairs that do hash to the same bucket are false positives; we hope these will be only a small fraction of all pairs. We also hope that most of the truly similar pairs will hash to the same bucket under at least one of the hash functions. Those that do not are false negatives; we hope these will be only a small fraction of the truly similar pairs.
If we have minhash signatures for the items, an effective way to choose the hashings is to divide the signature matrix into b bands consisting of r rows each. For each band, there is a hash function that takes vectors of r integers (the portion of one column within that band) and hashes them to some large number of buckets. We can use the same hash function for all the bands, but we use a separate bucket array for each band, so columns with the same vector in different bands will not hash to the same bucket.
Suppose we use b bands of r rows each, and suppose that a particular pair of documents have Jaccard similarity s. The probability the minhash signatures for these documents agree in any one particular row of the signature matrix is s. We can calculate the probability that these documents (or rather their signatures) become a candidate pair as follows:
- The probability that the signatures agree in all rows of one particular band is s r s^r sr.
- The probability that the signatures disagree in at least one row of a particular band is 1 − s r 1-s^r 1−sr.
- The probability that the signatures disagree in at least one row of each of the bands is ( 1 − s r ) b (1-s^r)^b (1−sr)b
- The probability that the signatures agree in all the rows of at least one band, and therefore become a candidate pair, is 1 − ( 1 − s r ) b 1-(1-s^r)^b 1−(1−sr)b.
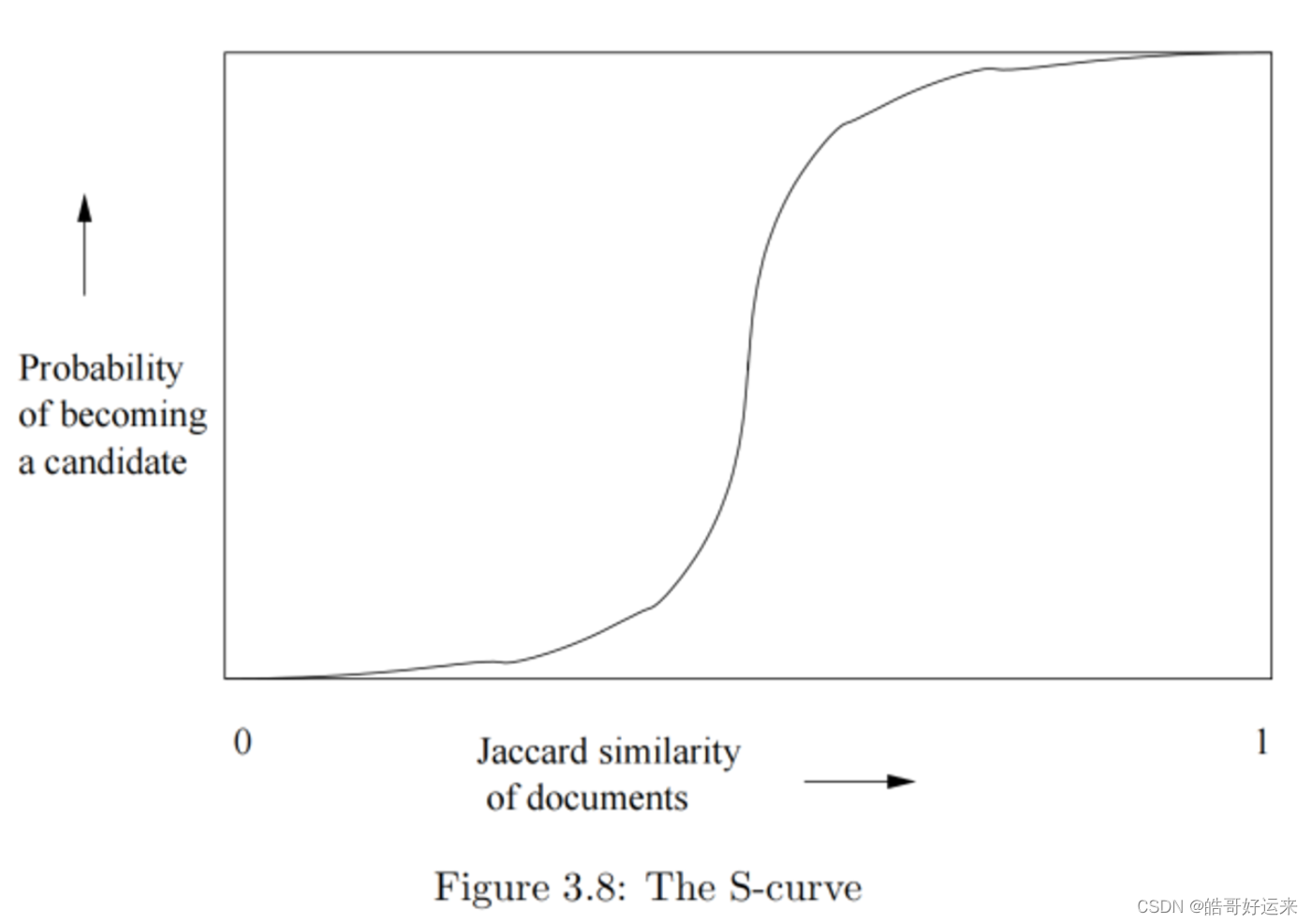
It may not be obvious, but regardless of the chosen constants b and r, this function has the form of an S-curve.
We can now give an approach to finding the set of candidate pairs for similar documents and then discovering the truly similar documents among them. It must be emphasized that this approach can produce false negatives – pairs of similar documents that are not identified as such because they never become a candidate pair. There will also be false positives – candidate pairs that are evaluated, but are found not to be sufficiently similar.
- Pick a value of k and construct from each document the set of k-shingles. Optionally, hash the k-shingles to shorter bucket numbers.
- Sort the document-shingle pairs to order them by shingle.
- Pick a length n for the minhash signatures. Feed the sorted list to the algorithm to compute the minhash signatures for all the documents.
- Choose a threshold t that defines how similar documents have to be in order for them to be regarded as a desired “similar pair.” Pick a number of bands b and a number of rows r such that b r = n br = n br=n, and the threshold t is approximately ( 1 / b ) 1 / r (1/b) ^{1/r} (1/b)1/r. If avoidance of false negatives is important, you may wish to select b and r to produce a threshold lower than t; if speed is important and you wish to limit false positives, select b and r to produce a higher threshold.
- Construct candidate pairs by applying the LSH technique.
- Examine each candidate pair’s signatures and determine whether the fraction of components in which they agree is at least t.
- Optionally, if the signatures are sufficiently similar, go to the documents themselves and check that they are truly similar, rather than documents that, by luck, had similar signatures
The LSH technique developed is one example of a family of functions (the minhash functions) that can be combined (by the banding technique) to distinguish strongly between pairs at a low distance from pairs at a high distance. The steepness of the S-curve in Fig. 3.8 reflects how effectively we can avoid false positives and false negatives among the candidate pairs. Now, we shall explore other families of functions, besides the minhash functions, that can serve to produce candidate pairs efficiently. These functions can apply to the space of sets and the Jaccard distance, or to another space and/or another distance measure. There are three conditions that we need for a family of functions:
- They must be more likely to make close pairs be candidate pairs than distant pairs.
- They must be statistically independent, in the sense that it is possible to estimate the probability that two or more functions will all give a certain response by the product rule for independent events.
- They must be efficient, in two ways:
(a) They must be able to identify candidate pairs in time much less than the time it takes to look at all pairs. For example, minhash functions have this capability, since we can hash sets to minhash values in time proportional to the size of the data, rather than the square of the number of sets in the data. Since sets with common values are colocated in a bucket, we have implicitly produced the candidate pairs for a single minhash function in time much less than
the number of pairs of sets.
(b) They must be combinable to build functions that are better at avoiding false positives and negatives, and the combined functions must also take time that is much less than the number of pairs. For example, the banding technique takes single minhash functions, which satisfy condition 3a but do not, by themselves have the S-curve behavior we want, and produces from a number of minhash functions a combined function that has the S-curve shape.
Locality-Sensitive Functions
For the purposes of this section, we shall consider functions that take two items and render a decision about whether these items should be a candidate pair.
In many cases, the function f will “hash” items, and the decision will be based on whether or not the result is equal. Because it is convenient to use the notation f ( x ) = f ( y ) f(x) = f(y) f(x)=f(y) to mean that f(x, y) is “yes; make x and y a candidate pair,” we shall use f ( x ) = f ( y ) f(x) = f(y) f(x)=f(y) as a shorthand with this meaning. We also use f ( x ) ≠ f ( y ) f(x) \not = f(y) f(x)=f(y) to mean “do not make x and y a candidate pair unless some other function concludes we should do so.”
A collection of functions of this form will be called a family of functions.
For example, the family of minhash functions, each based on one of the possible permutations of rows of a characteristic matrix, form a family.
Let d 1 < d 2 d_1 < d_2 d1<d2 be two distances according to some distance measure d. A family F of functions is said to be (d1, d2, p1, p2)-sensitive if for every f in F:
- If d ( x , y ) ≤ d 1 d(x, y) ≤ d_1 d(x,y)≤d1, then the probability that f(x) = f(y) is at least p 1 p_1 p1.
- If d ( x , y ) ≥ d 2 d(x, y) ≥ d_2 d(x,y)≥d2, then the probability that f(x) = f(y) is at most p 2 p_2 p2.
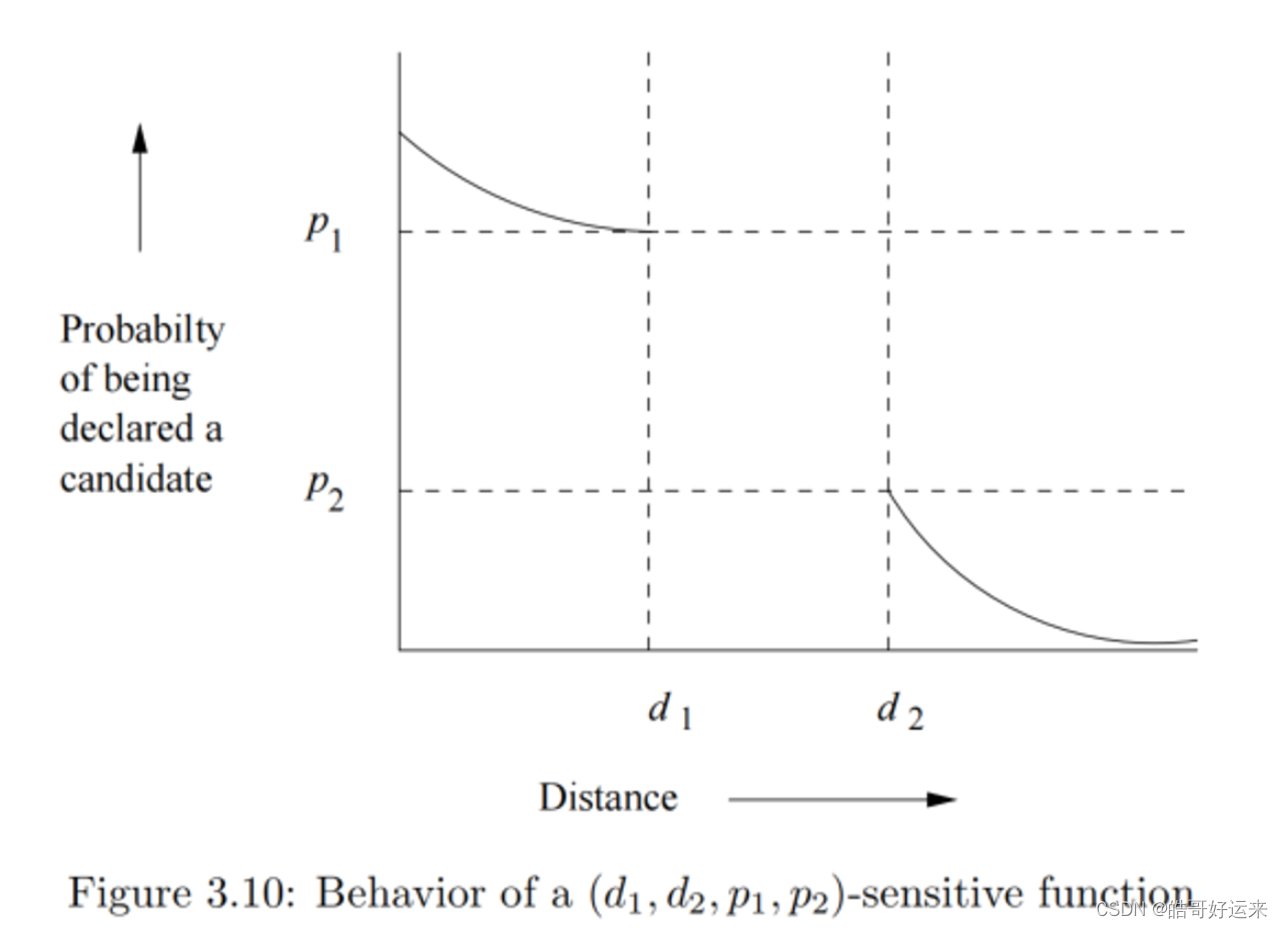
Suppose we are given a (d1, d2, p1, p2)-sensitive family F. We can construct a new family F′ by the AND-construction on F, which is defined as follows. Each member of F′ consists of r members of F for some fixed r. If f is in F′, and f is constructed from the set f 1 , f 2 , . . . , f r {f_1, f_2, . . . , f_r} f1,f2,...,fr of members of F, we say f(x) = f(y) if and only if f i ( x ) = f i ( y ) f_i(x) = f_i(y) fi(x)=fi(y) for all i = 1, 2, . . . , r. Notice that this construction mirrors the effect of the r rows in a single band: the band makes x and y a candidate pair if every one of the r rows in the band say that x and y are equal (and therefore a candidate pair according to that row).
Since the members of F are independently chosen to make a member of F′, we can assert that F′ is a ( d 1 , d 2 , ( p 1 ) r , ( p 2 ) r ) (d_1,d_2,(p_1)^r,(p_2)^r) (d1,d2,(p1)r,(p2)r) - sensitive family. That is, for any p, if p is the probability that a member of F will declare (x, y) to be a candidate pair, then the probability that a member of F′ will so declare is p r p^r pr.
There is another construction, which we call the OR-construction, that turns
a (d1, d2, p1, p2)-sensitive family F into a ( d 1 , d 2 , 1 − ( 1 − p 1 ) b , 1 − ( 1 − p 2 ) b ) (d_1,d_2,1-(1-p_1)^b,1-(1-p_2)^b) (d1,d2,1−(1−p1)b,1−(1−p2)b)
sensitive family F′. Each member f of F′ is constructed from b members of F, say f 1 , f 2 , . . . , f b f_1, f_2, . . . , f_b f1,f2,...,fb. We define f(x) = f(y) if and only if f i ( x ) = f i ( y ) f_i(x) = f_i(y) fi(x)=fi(y) for one or more values of i. The OR-construction mirrors the effect of combining several bands: x and y become a candidate pair if any band makes them a candidate pair.
Summary of Chapter 3
- Jaccard Similarity: The Jaccard similarity of sets is the ratio of the size of the intersection of the sets to the size of the union. This measure of similarity is suitable for many applications, including textual similarity of documents and similarity of buying habits of customers.
- Shingling: A k-shingle is any k characters that appear consecutively in a document. If we represent a document by its set of k-shingles, then the Jaccard similarity of the shingle sets measures the textual similarity of documents. Sometimes, it is useful to hash shingles to bit strings of shorter length, and use sets of hash values to represent documents.
- Minhashing: A minhash function on sets is based on a permutation of the universal set. Given any such permutation, the minhash value for a set is that element of the set that appears first in the permuted order.
- Minhash Signatures: We may represent sets by picking some list of permutations and computing for each set its minhash signature, which is the sequence of minhash values obtained by applying each permutation on the list to that set. Given two sets, the expected fraction of the permutations that will yield the same minhash value is exactly the Jaccard similarity of the sets.
- Efficient Minhashing: Since it is not really possible to generate random permutations, it is normal to simulate a permutation by picking a random hash function and taking the minhash value for a set to be the least hash value of any of the set’s members. An additional efficiency can be had by restricting the search for the smallest minhash value to only a small subset of the universal set.
- Locality-Sensitive Hashing for Signatures: This technique allows us to avoid computing the similarity of every pair of sets or their minhash signatures. If we are given signatures for the sets, we may divide them into bands, and only measure the similarity of a pair of sets if they are identical in at least one band. By choosing the size of bands appropriately, we can eliminate from consideration most of the pairs that do not meet our threshold of similarity.
- Distance Measures: A distance measure is a function on pairs of points in a space that satisfy certain axioms. The distance between two points is 0 if the points are the same, but greater than 0 if the points are different. The distance is symmetric; it does not matter in which order we consider the two points. A distance measure must satisfy the triangle inequality: the distance between two points is never more than the sum of the distances between those points and some third point.
- Euclidean Distance: The most common notion of distance is the Euclidean distance in an n-dimensional space. This distance, sometimes called the L2-norm, is the square root of the sum of the squares of the differences between the points in each dimension. Another distance suitable for Euclidean spaces, called Manhattan distance or the L1-norm is the sum of the magnitudes of the differences between the points in each dimension.
- Jaccard Distance: One minus the Jaccard similarity is a distance measure, called the Jaccard distance.
- Cosine Distance: The angle between vectors in a vector space is the cosine distance measure. We can compute the cosine of that angle by taking the dot product of the vectors and dividing by the lengths of the vectors.
- Edit Distance: This distance measure applies to a space of strings, and is the number of insertions and/or deletions needed to convert one string into the other. The edit distance can also be computed as the sum of the lengths of the strings minus twice the length of the longest common subsequence of the strings.
- Hamming Distance: This distance measure applies to a space of vectors. The Hamming distance between two vectors is the number of positions in which the vectors differ.
- Generalized Locality-Sensitive Hashing: We may start with any collection of functions, such as the minhash functions, that can render a decision as to whether or not a pair of items should be candidates for similarity checking. The only constraint on these functions is that they provide a lower bound on the probability of saying “yes” if the distance (according to some distance measure) is below a given limit, and an upper bound on the probability of saying “yes” if the distance is above another given limit. We can then increase the probability of saying “yes” for nearby items and at the same time decrease the probability of saying “yes” for distant items to as great an extent as we wish, by applying an AND construction and an OR construction.
- Random Hyperplanes and LSH for Cosine Distance: We can get a set of basis functions to start a generalized LSH for the cosine distance measure by identifying each function with a list of randomly chosen vectors. We apply a function to a given vector v by taking the dot product of v with each vector on the list. The result is a sketch consisting of the signs (+1 or −1) of the dot products. The fraction of positions in which the sketches of two vectors agree, multiplied by 180, is an estimate of the angle between the two vectors.
- LSH For Euclidean Distance: A set of basis functions to start LSH for Euclidean distance can be obtained by choosing random lines and projecting points onto those lines. Each line is broken into fixed-length intervals, and the function answers “yes” to a pair of points that fall into the same interval.
- High-Similarity Detection by String Comparison: An alternative approach to finding similar items, when the threshold of Jaccard similarity is close to 1, avoids using minhashing and LSH. Rather, the universal set is ordered, and sets are represented by strings, consisting their elements in order. The simplest way to avoid comparing all pairs of sets or their strings is to note that highly similar sets will have strings of approximately the same length. If we sort the strings, we can compare each string with only a small number of the immediately following strings.
- Character Indexes: If we represent sets by strings, and the similarity threshold is close to 1, we can index all strings by their first few characters. The prefix whose characters must be indexed is approximately the length of the string times the maximum Jaccard distance (1 minus the minimum Jaccard similarity).
- Position Indexes: We can index strings not only on the characters in their prefixes, but on the position of that character within the prefix. We reduce the number of pairs of strings that must be compared, because if two strings share a character that is not in the first position in both strings, then we know that either there are some preceding characters that are in the union but not the intersection, or there is an earlier symbol that appears in both strings.
- Suffix Indexes: We can also index strings based not only on the characters in their prefixes and the positions of those characters, but on the length of the character’s suffix – the number of positions that follow it in the string. This structure further reduces the number of pairs that must be compared, because a common symbol with different suffix lengths implies additional characters that must be in the union but not in the intersection.
END
ps. 终于看完了,下一本书跨专业咯:《营销管理》(第15版)
相关文章:

《斯坦福数据挖掘教程·第三版》读书笔记(英文版)Chapter 3 Finding Similar Items
来源:《斯坦福数据挖掘教程第三版》对应的公开英文书和PPT It is therefore a pleasant surprise to learn of a family of techniques called locality-sensitive hashing, or LSH, that allows us to focus on pairs that are likely to be similar, without hav…...
天眼销:超有用的企业获客工具
天眼销是资深数据团队开发的一个客户资源查询平台,可以通过多重筛选:企业名称/信用代码,所在地区,行业,注册资本,年限,是否在营/有电话/邮箱等。 天眼销和某查查有什么区别? 天*查/…...
dbeaver连接amabri-hbase
目录 尝试过程 解决之道 总结 尝试过程 注意此章节为记录试错过程,无需跟随操作,仅作试错记录。真正操作方法请看“解决之道”章节 环境ambari安装的hbase2.1.6 使用apche phoenix默认驱动配置 备注:Apache Phoenix 是一个开源的、基于…...

Mac IDEA解决Maven项目命令行报错:command not found: mvn
1. 使用idea自带的maven命令 open -e ~/.zshrc 2. 在其最下面增加 # maven export MAVEN_HOME"/Applications/IntelliJ IDEA.app/Contents/plugins/maven/lib/maven3" export PATH$MAVEN_HOME/bin:$PATH # maven end 3. 连接使之生效 source ~/.zshrc4. 修改mvn…...

线性回归 梯度下降
梯度下降算法 在开始之前,为了方便解释,首先规定几个符号所代表的意义: m m m 训练集中训练样本的数量 X X X 输入变量 Y Y Y 输出变量 ( x , y ) (x,y) (x,y) 训练样本 ( x i , y i ) (x^i,y^i) (xi,yi)第i个训练样本(i表示…...

[Linux]进程等待
文章目录 3.进程等待3.1什么是进程等待3.2为什么要进程等待3.3如何进行进程等待?1.wait2.waitpid2.1函数的讲解2.2status的理解2.3代码理解 3.4学后而思1.直接用全局变量获取子进程退出码可以吗?如下2.进程具有独立性 退出码是子进程的数据 父进程是如何拿到退出码的3.对内存…...

Project DESFT 白皮书中文版——应用于普惠金融的可信数字凭证解决方案
1. 概述 Project DESFT 是由 Solv 基金会与 zCloak Network 联合设计孵化,以跨境贸易和金融服务为场景的分布式可信数字凭证解决方案(Distributed Trusted Digital Credential Solution),项目获得新加坡金管局(Monetar…...

907. 子数组的最小值之和 --力扣 --JAVA
题目 给定一个整数数组 arr,找到 min(b) 的总和,其中 b 的范围为 arr 的每个(连续)子数组。 由于答案可能很大,因此 返回答案模 10^9 7 。 解题思路 找到以当前值为最小值所能组成的子数组;若存在两个相同…...

3D模型渲染导致电脑太卡怎么办?
在线工具推荐: 三维数字孪生场景工具 - GLTF/GLB在线编辑器 - Three.js AI自动纹理化开发 - YOLO 虚幻合成数据生成器 - 3D模型在线转换 - 3D模型预览图生成服务 1、什么是3D渲染? 3D渲染是指通过计算机图形学技术将三维模型转化为二维图像的过程…...

构建个人代理池:使用GitHub项目proxy_pool的搭建配置及代码接口详解
手把手教你搭建代理IP池: 项目简介: 爬虫代理IP池项目,主要功能为定时采集网上发布的免费代理验证入库,定时验证入库的代理保证代理的可用性,提供API和CLI两种使用方式。同时你也可以扩展代理源以增加代理池IP的质量和数量。…...

Pytorch进阶教学——训练一个图像分类模型(GPU)
目录 1、前言 2、数据集介绍 3、获取数据 4、创建网络 5、训练模型 6、测试模型 6.1、测试整个模型准确率 6.2、测试单张图片 1、前言 编写一个可以分类蚂蚁和蜜蜂图片的模型,使用数据集对卷积神经网络进行训练。训练后的模型可以对蚂蚁或蜜蜂的图片进行…...

Docker Swarm总结+CI/CD Devops、gitlab、sonarqube以及harbor的安装集成配置(3/5)
博主介绍:Java领域优质创作者,博客之星城市赛道TOP20、专注于前端流行技术框架、Java后端技术领域、项目实战运维以及GIS地理信息领域。 🍅文末获取源码下载地址🍅 👇🏻 精彩专栏推荐订阅👇🏻…...

Linux:windows 和 Linux 之间文本格式转换
背景 在 Windows 上编辑的文件,放到 Linux 平台,有时会出现奇怪的问题,其中有一个是 ^M 引起的,例如这种错误: /bin/bash^M: bad interpreter 这个问题相信大家也碰到过,原因是 Windows 和 Linux 关于换行的…...
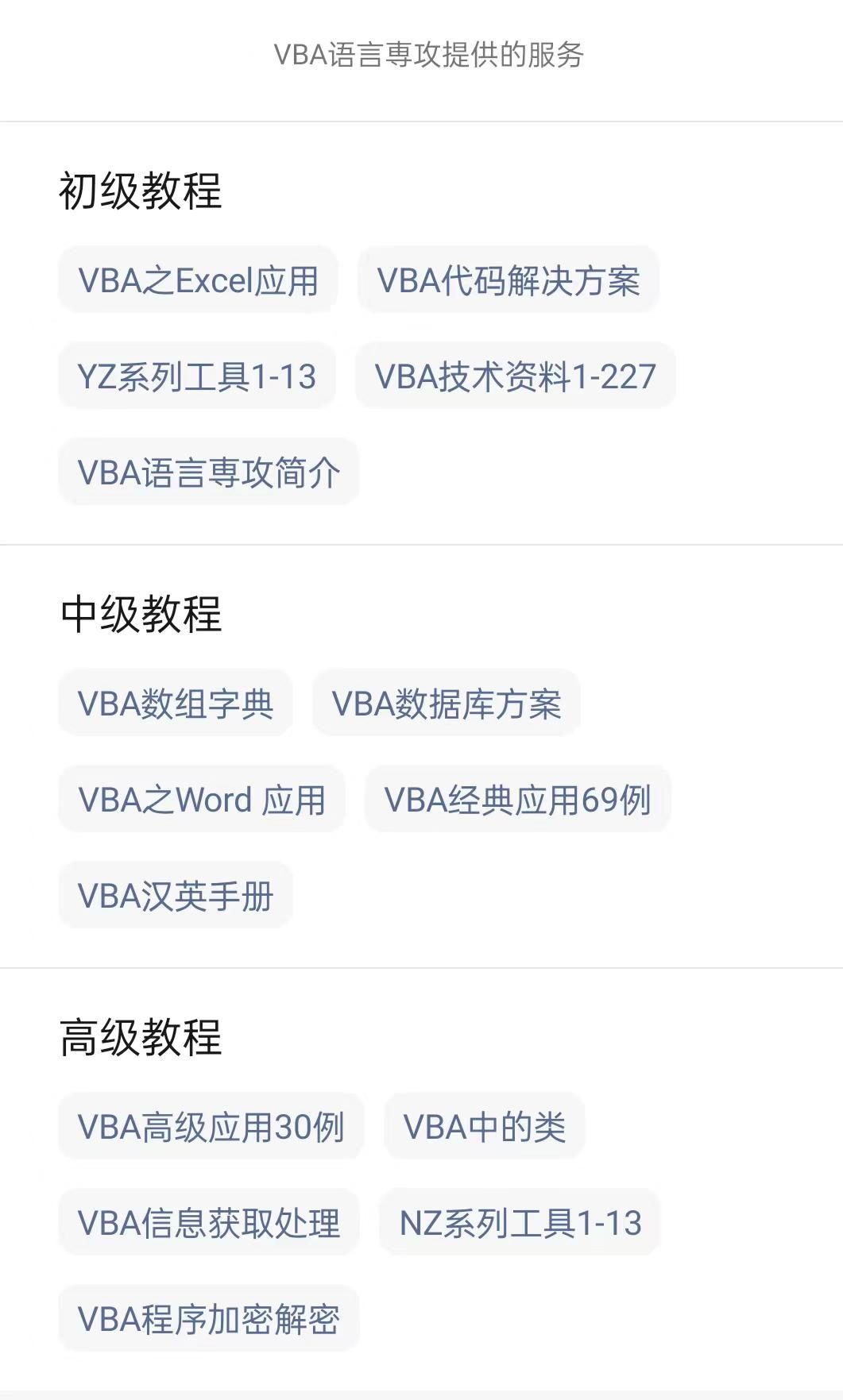
VBA技术资料MF88:测试Excel文件名是否有效
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到…...

u8g2图形库——丝滑菜单制作
目录 一、实物效果展示 二、丝滑菜单实现原理 三、代码开源 1.ui_bmp.h 2.ui.h 3.ui.c 一、实物效果展示 u8g2图形库——丝滑菜单制作 二、丝滑菜单实现原理 int ui_run(short *a,short *a_tag,uint8_t step,uint8_t slow_cnt) //UI滑动效果 {uint8_t temp;…...

Go 异常处理流程
在 Go 语言中,panic、recover 和 defer 是用于处理异常情况的关键字。它们通常一起使用来实现对程序错误的处理和恢复。 1. defer 语句 defer 用于在函数返回之前执行一段代码。被 defer 修饰的语句或函数会在包含 defer 的函数执行完毕后执行。defer 常用于资源清…...
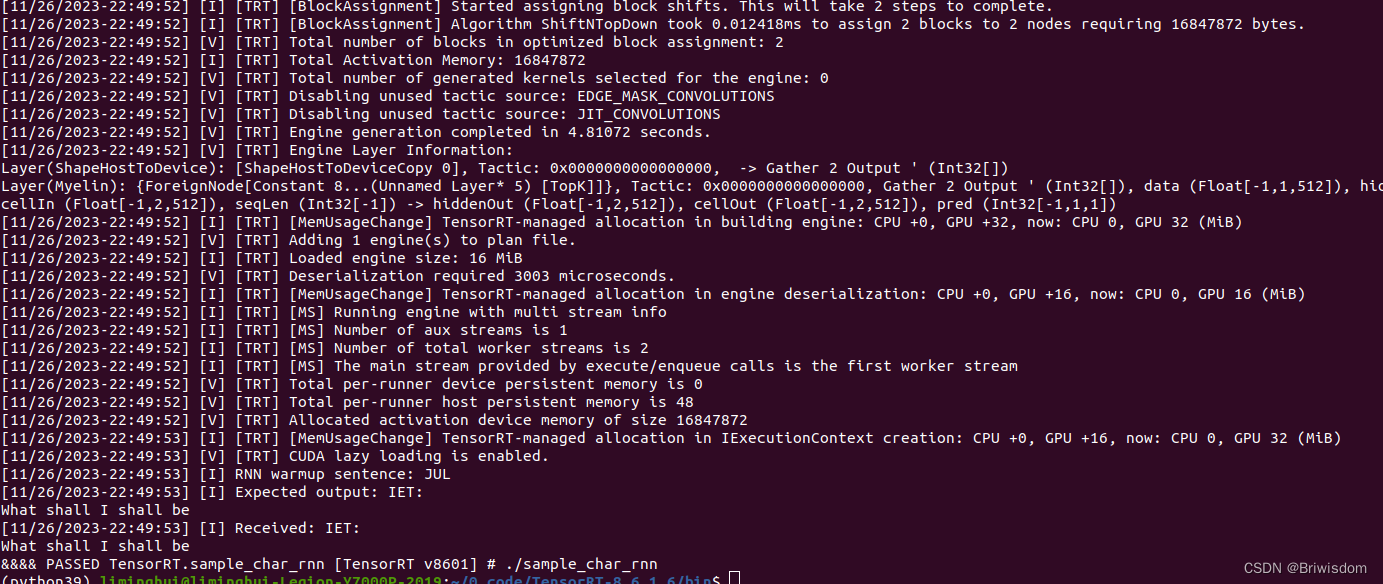
ubuntu20.04安装tensorRT流程梳理
目标:先跑demo,再学习源码 step1, 提前准备好CUDA环境 安装CUDA,cuDNN 注意,CUDA,cuDNN需要去官网下载.run和tar文件安装,否则在下面step4 make命令会报找不到cuda等的错误,具体安装教程网上…...

数字孪生技术:提升UI交互性与个性化设计
随着数字化时代的到来,数字孪生技术正在逐渐改变我们的生活和工作方式。数字孪生是一种复制现实世界系统或实体的技术,通过创建数字模型来模拟现实世界中的各种行为和事件。这种技术不仅为人们提供了一个全新的视角来看待和解决问题,同时也为…...

外包干了5个月,技术退步明显.......
先说一下自己的情况,大专生,18年通过校招进入武汉某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落! 而我已经在一个企业干了四年的功能测…...
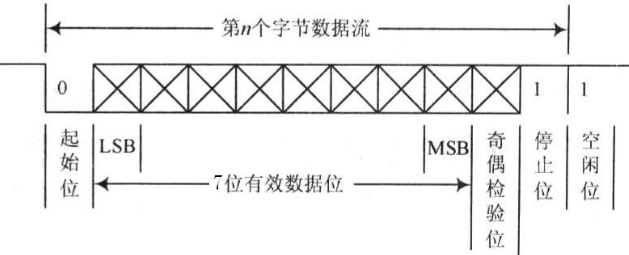
嵌入式常见的几种接口
嵌入式开发中,常见的外设通信接口/协议有SPI,I2C,UART三种,本文先分三个部分对SPI,I2C,UART进行介绍,最后对这三种协议进行比较。 1 SPI 1.1 SPI的简介 SPI(Serial Peripheral …...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...
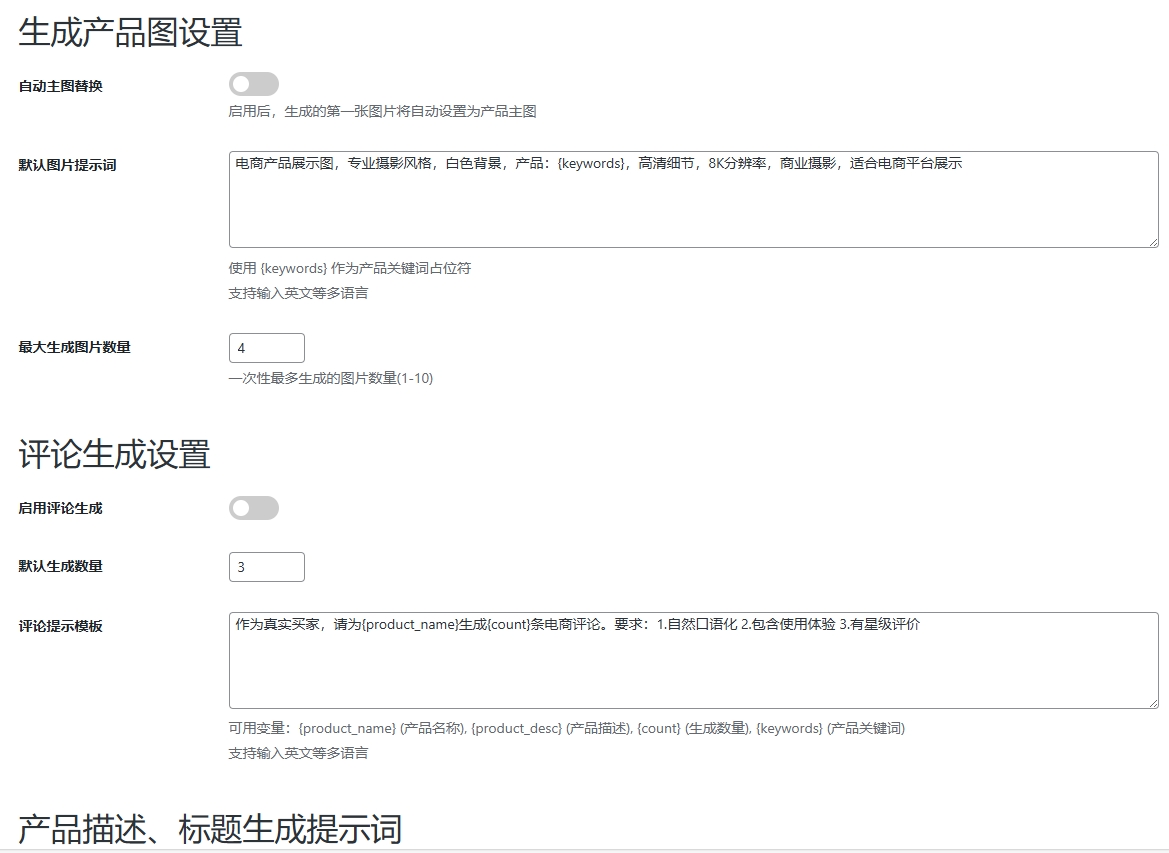
WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
