智能优化算法应用:基于蝴蝶算法无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于蝴蝶算法无线传感器网络(WSN)覆盖优化 - 附代码
文章目录
- 智能优化算法应用:基于蝴蝶算法无线传感器网络(WSN)覆盖优化 - 附代码
- 1.无线传感网络节点模型
- 2.覆盖数学模型及分析
- 3.蝴蝶算法
- 4.实验参数设定
- 5.算法结果
- 6.参考文献
- 7.MATLAB代码
摘要:本文主要介绍如何用蝴蝶算法进行无线传感器网(WSN)覆盖优化。
1.无线传感网络节点模型
本文主要基于0/1模型,进行寻优。在二维平面上传感器节点的感知范围是一个以节点为圆心,半径为 R n R_n Rn的圆形区域,该圆形区域通常被称为该节点的“感知圆盘”, R n R_n Rn称为传感器节点的感知半径,感知半径与节点内置传感器件的物理特性有关,假设节点 n n n的位置坐标为 ( x n , y n ) (x_n,y_n) (xn,yn)在0-1感知模型中,对于平面上任意一点 p ( x p , y p ) p(x_p,y_p) p(xp,yp),则节点 n n n监测到区域内点 p p p的事件发生概率为:
P r ( n , p ) = { 1 , d ( n , p ) ≤ R n 0 , e s l e (1) P_r(n,p)=\begin{cases}1, \,d(n,p)\leq R_n\\ 0,\, esle \end{cases}\tag{1} Pr(n,p)={1,d(n,p)≤Rn0,esle(1)
其中 d ( n , p ) = ( x n − x p ) 2 + ( y n − y p ) 2 d(n,p)=\sqrt{(x_n-x_p)^2+(y_n-y_p)^2} d(n,p)=(xn−xp)2+(yn−yp)2为点和之间的欧式距离。
2.覆盖数学模型及分析
现假定目标监测区域为二维平面,在区域 A r e a Area Area上投放同型结构传感器节点的数目为N,每个节点的位置坐标值假设已被初始化赋值,且节点的感知半径r。传感器节点集则表示为:
N o d e { x 1 , . . . , x N } (2) Node\{x_1,...,x_N\} \tag{2} Node{x1,...,xN}(2)
其中 n o d e i = { x i , y i , r } node_i=\{x_i,y_i,r\} nodei={xi,yi,r},表示以节点 ( x i , y i ) (x_i,y_i) (xi,yi)为圆心,r为监测半径的圆,假定监测区域 A r e a Area Area被数字化离散为 m ∗ n m*n m∗n个像素点,像素点的坐标为 ( x , y ) (x,y) (x,y),目标像素点与传感器节点间的距离为:
d ( n o d e i , p ) = ( x i − x ) 2 + ( y i − y ) 2 (3) d(node_i,p)=\sqrt{(x_i-x)^2+(y_i-y)^2}\tag{3} d(nodei,p)=(xi−x)2+(yi−y)2(3)
目标区域内像素点被传感器节点所覆盖的事件定义为 c i c_i ci。则该事件发生的概率 P c i P{c_i} Pci即为像素点 ( x , y ) (x,y) (x,y)被传感器节点 n o d e i node_i nodei所覆盖的概率:
P c o v ( x , y , n o d e i ) = { 1 , i f d ( n o d e i , p ) ≤ r 0 , e s l e (4) P_{cov}(x,y,node_i)=\begin{cases}1, if\,d(node_i,p)\leq r\\ 0,\, esle \end{cases}\tag{4} Pcov(x,y,nodei)={1,ifd(nodei,p)≤r0,esle(4)
我们将所有的传感器节点在目标监测环境中的区域覆盖率 C o v e r R a t i o CoverRatio CoverRatio定义为传感器节点集的覆盖面积与监测区域的面积之比,如公式所示:
C o v e r R a t i o = ∑ P c o v m ∗ n (5) CoverRatio = \frac{\sum P_{cov}}{m*n}\tag{5} CoverRatio=m∗n∑Pcov(5)
那我们的最终目标就是找到一组节点使得覆盖率最大。
3.蝴蝶算法
蝴蝶算法原理请参考:https://blog.csdn.net/u011835903/article/details/107855860
该算法是寻找最小值。于是适应度函数定义为未覆盖率最小,即覆盖率最大。如下:
f u n = a r g m i n ( 1 − C o v e r R a t i o ) = a r g m i n ( 1 − ∑ P c o v m ∗ n ) (6) fun = argmin(1 - CoverRatio) = argmin(1-\frac{\sum P_{cov}}{m*n}) \tag{6} fun=argmin(1−CoverRatio)=argmin(1−m∗n∑Pcov)(6)
4.实验参数设定
无线传感器覆盖参数设定如下:
%% 设定WNS覆盖参数,
%% 默认输入参数都是整数,如果想定义小数,请自行乘以系数变为整数再做转换。
%% 比如范围1*1,R=0.03可以转换为100*100,R=3;
%区域范围为AreaX*AreaY
AreaX = 100;
AreaY = 100;
N = 20 ;%覆盖节点数
R = 15;%通信半径蝴蝶算法参数如下:
%% 设定优化参数
pop=30; % 种群数量
Max_iteration=80; %设定最大迭代次数
lb = ones(1,2*N);
ub = [AreaX.*ones(1,N),AreaY.*ones(1,N)];
dim = 2*N;%维度为2N,N个坐标点
5.算法结果

从结果来看,覆盖率在优化过程中不断上升,表明蝴蝶算法对覆盖优化起到了优化的作用。
6.参考文献
[1] 史朝亚. 基于PSO算法无线传感器网络覆盖优化的研究[D]. 南京理工大学.
7.MATLAB代码
相关文章:

智能优化算法应用:基于蝴蝶算法无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于蝴蝶算法无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于蝴蝶算法无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.蝴蝶算法4.实验参数设定5.算法结果6.参考文献7.MATLAB…...
3dsMax插件Datasmith Exporter安装使用方法
3dsMax插件Datasmith Exporter安装使用方法 某些文件格式无法用Datasmith直接导入虚幻引擎,这些数据必须先被转换为Datasmith能够识别的文件格式。Datasmith Exporter插件就可以帮助您的软件导出可以被Datasmith导入虚幻引擎的.udatasmith格式文件。 在开始使用虚幻…...
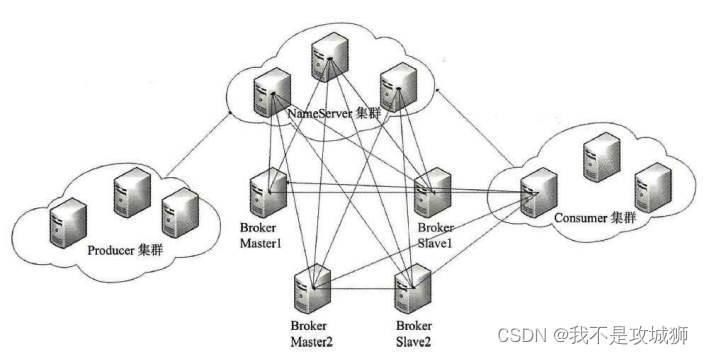
Rocketmq架构
NameServer:作为注册中心,提供路由注册、路由踢出、路由发现功能,舍弃强一致,保证高可用,集群中各个节点不会实时通讯,其中一个节点下线之后,会提供另外一个节点保证路由功能。 Rocket mq name…...

中兴亮相中国国际现代化铁路技术装备展览会 筑智铁路5G同行
近日,第十六届中国国际现代化铁路技术装备展览会在北京中国国际展览中心举办,中兴以“数智铁路,5G同行”主题亮相本次展览会,并全面展示了“数字铁路网络基础设施”、“云边结合的铁路行业云”、“数字铁路赋能赋智”等方面的最新…...

从零学算法15
15.给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元组。 示例 …...

《Effective C++》条款27
尽量少做转型动作 class A { public:A(int x) :a(x) {};virtual void add(){a;} private:int a; }; class B :public A { public:B(int x) :b(x),A(x) {};virtual void add(){static_cast<A>(*this).add();b;}private:int b; }; 如上描述把子类转型为A类,调用…...

无图谱不AI之三元组数据保存Neo4j
目录 1. 代码学习1.1 源代码1.2 代码解读 没有图谱称为弱人工智能,有图谱的称为强人工智能。 图谱可以让机器学习和人工智能具备推理能力。 1. 代码学习 1.1 源代码 # -*- coding: utf-8 -*- from py2neo import Node, Graph, Relationship# 可以先阅读下文档&a…...
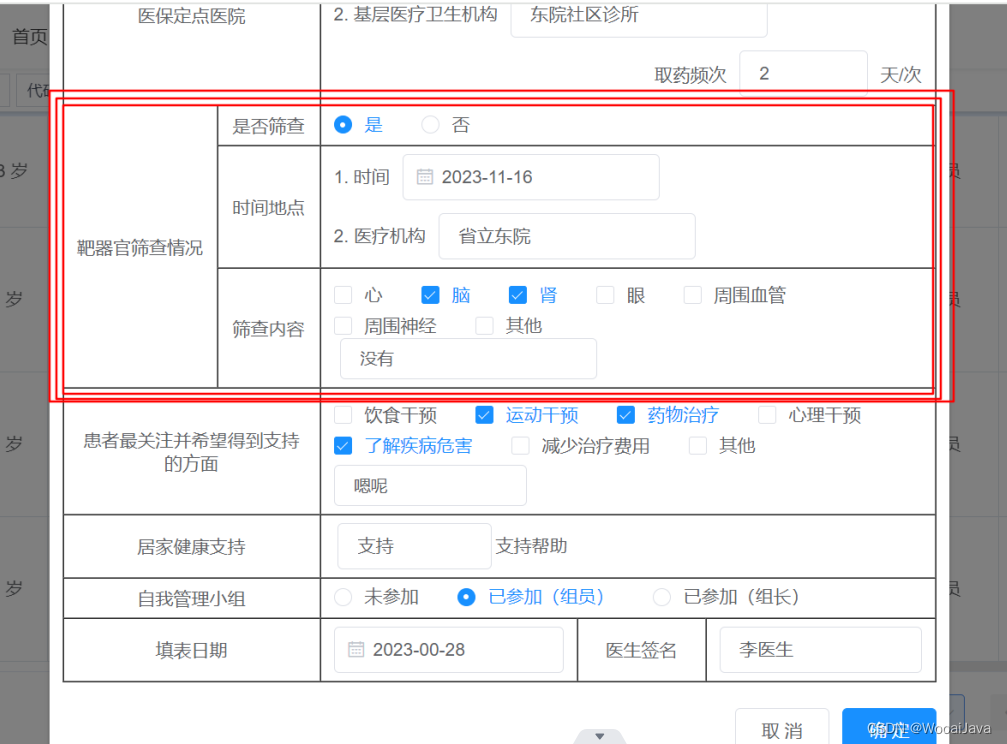
Mybatisplus同时向两张表里插入数据[事务的一致性]
一、需求:把靶器官的数据,单独拿出来作为一个从表,以List的方式接收这段数据; 此时分析,是需要有两个实体的,一个是主表的实体,一个是从表的实体,并在主表实体新增一个List 字段来接…...

天眼销:精准的企业名录
企业名录的重要性,对于销售而言都是极其重要的。本期为家人们分享如何正确挑选出优质的企业名录渠道,避免走一些弯弯坑坑。 为了有效利用企业名录进行客户开发,您需要关注信息的准确性、可提供的资源数量以及信息的时效性。能否根据您的需求…...
)
TypeError: Cannot read properties of null (reading ‘shapeFlag‘)
vue3 开发过程遇到这样一个报错 TypeError: Cannot read properties of null (reading shapeFlag)最后发现是ref定义的变量,在访问时没有使用.valuereactive 变量初始化是数组,如果使用字符串赋值时也会报这个错。...
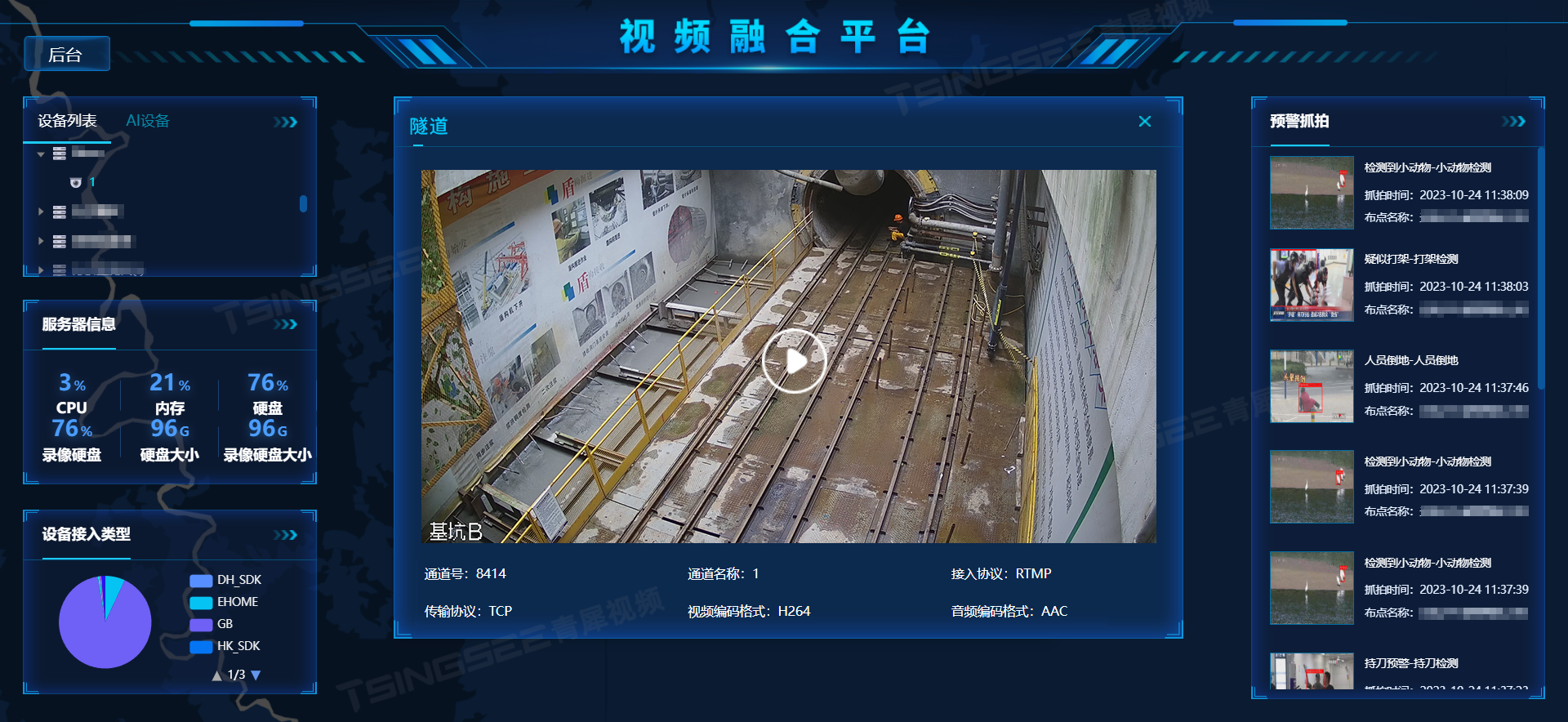
视频监控平台EasyCVR多场景应用,AI视频分析技术助力行业升级转型
传统的视频监控系统建设,经常存在各方面的因素制约,造成管理机制不健全、统筹规划不到位、联网共享不规范,形成“信息孤岛”、“数据烟囱”。在监控系统的建设中缺乏统一规划,标准不统一、视频图像信息利用率低等问题日益突出。随…...
如何搭建外网可访问的Serv-U FTP服务器,轻松远程共享文件!
目录 1. 前言 2. 本地FTP搭建 2.1 Serv-U下载和安装 2.2 Serv-U共享网页测试 2.3 Cpolar下载和安装 3. 本地FTP发布 3.1 Cpolar云端设置 3.2 Cpolar本地设置 4. 公网访问测试 5. 总结 1. 前言 科技日益发展的今天,移动电子设备似乎成了我们生活的主角&am…...

c++--类型的基础
1.常量对象,常量成员函数 (1).常量对象 常量对象的引用和指针不能调用类的普通的成员函数。只能调用常量成员函数。 (2).常量成员函数:把const放在类成员函数参数列表后。表示隐含的this是一个指向常量的指针 (3).当创建一个const对象时,直到…...

Python with提前退出:坑与解决方案
Python with提前退出:坑与解决方案 问题的起源 早些时候使用with实现了一版全局进程锁,希望实现以下效果: Python with提前退出:坑与解决方案 全局进程锁本身不用多说,大部分都依靠外部的缓存来实现的,r…...
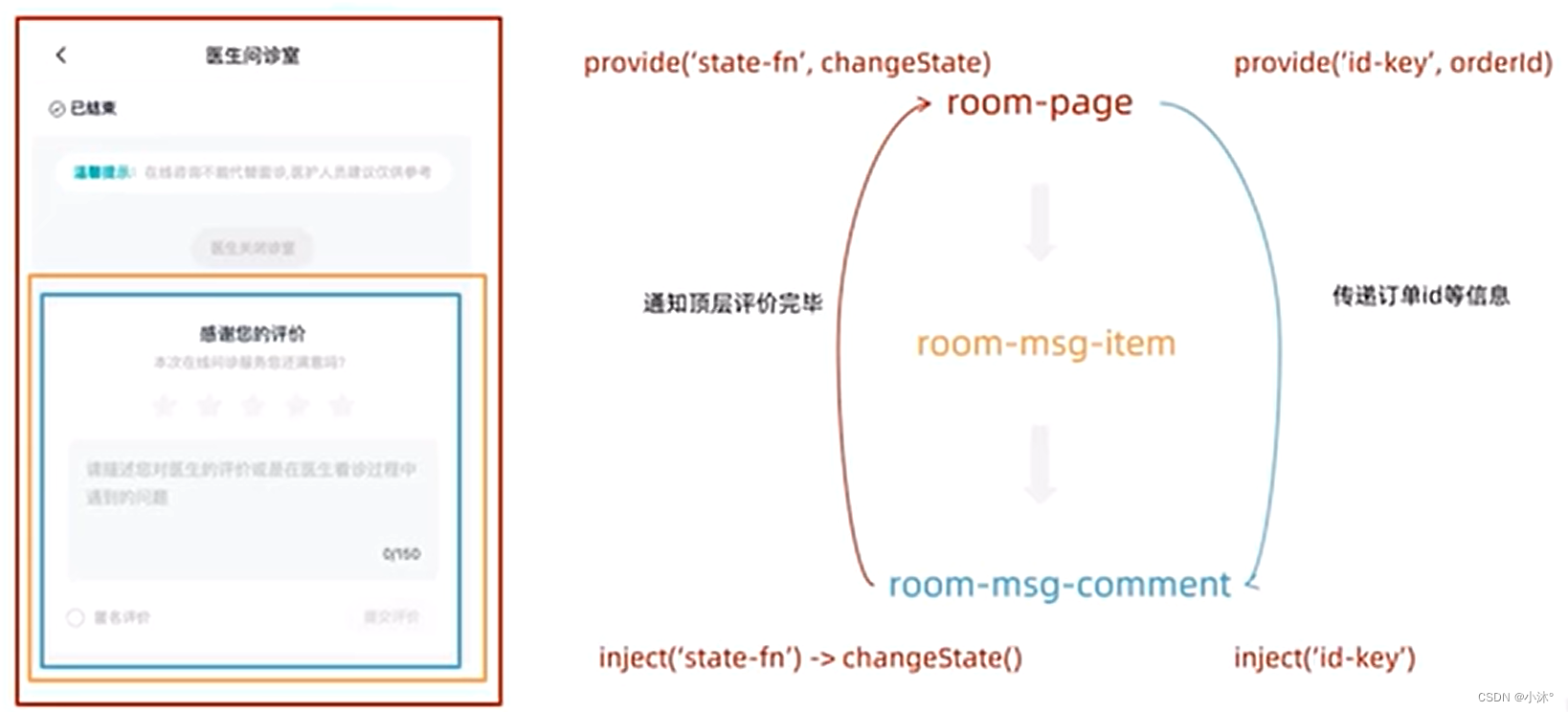
Vue3-provide和inject
作用和场景:顶层组件向任意的底层组件传递数据和方法,实现跨层组件通信 跨层传递普通数据: 1.顶层组件通过provide函数提供数据 2.底层组件通过inject函数获取数据 既可以传递普通数据,也可以使用ref传递响应式数据(…...

Python与设计模式--适配器模式
23种计模式之 前言 (5)单例模式、工厂模式、简单工厂模式、抽象工厂模式、建造者模式、原型模式、(7)代理模式、装饰器模式、适配器模式、门面模式、组合模式、享元模式、桥梁模式、(11)策略模式、责任链模式、命令模式、中介者模…...
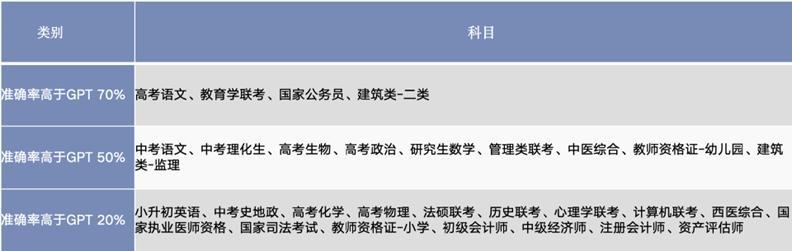
大模型能否生成搜索引擎的未来?
文|郝 鑫 编|刘雨琦 ChatGPT火爆之前,水面下,也有中国公司也在朝着智能助手的方向努力。夸克便是其中之一。在GPT风靡科技圈后,国内就开始陆续冒出一些大模型厂商。对当时夸克而言,做大模型毋庸置疑&am…...

鸿蒙开发-ArkTS 语言-状态管理
[写在前面: 文章多处用到gif动图,如未自动播放,请点击图片] 衔接上一篇:鸿蒙开发-ArkTS 语言-基础语法 3. 状态管理 变量必须被装饰器装饰才能成为状态变量,状态变量的改变才能导致 UI 界面重新渲染 概念描述状态变量被状态装饰器装饰的变…...

一篇文章带你掌握MongoDB
文章目录 1. 前言2. MongoDB简介3. MongoDB与关系型数据库的对比4. MongoDB的安装5. Compass的使用6. MongoDB的常用语句7. 总结 1. 前言 本文旨在帮助大家快速了解MongoDB,快速了解和掌握MongoDB的干货内容. 2. MongoDB简介 MongoDB是一种NoSQL数据库,采用了文档…...

删除docker镜像
随着我们拉取的镜像越来越多,镜像的管理越来越难。这时候可能就需要删除镜像了。 本关的任务是学习如何删除容器,要求学习者参照示例,将busybox:latest镜像删除。 相关知识 删除镜像 如果要删除本地的镜像,可以使用 docker rm…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...
