从零学算法15
15.给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
- 我的原始人题解:如果题目为两数之和等于某数,那么可以将数组排序后用两个指针从左右两端开始找,当和过大则右指针左移,和过小则左指针右移,否则记录当前可能然后左右指针挑一个移动。比如数组 [1,2,3,4,5] 要找和为 5 的两个数,首先左右两指针分别指向 [1,5],此时和为 6 大于 5,所以应该减小和,即右指针左移;此时为 [1,4] 符合条件并记录,比如这时右指针左移,然后得到 [1,3] 发现和为 4 过小,所以左指针右移来增加和,得到 [2,3] 满足条件并记录。
- 那么三数之和也是基于同样的思路,用三个指针来表示三个数,固定其中一个,然后剩下两个指针寻找结果,为了去重,所以先使用 set 记录结果
-
public List<List<Integer>> threeSum(int[] nums) {Set<List<Integer>> res = new HashSet<>();Arrays.sort(nums);int n = nums.length;// 因为至少要三个数,所以到 n-2 即可for(int i=0;i<n-2;i++){// i 在遍历时其实就表示每次固定的那一位// j 每次从 i 后一位开始// k 每次从最右端开始int j=i+1,k=n-1;while(j<k){int tmp = nums[i]+nums[j]+nums[k];if(tmp == 0){res.add(new ArrayList<Integer>(Arrays.asList(nums[i],nums[j],nums[k])));}if(tmp > 0)k--;else if(tmp <= 0)j++;}}ArrayList<List<Integer>> ans = new ArrayList<>(res);return ans;} - 他人优化版本
-
public List<List<Integer>> threeSum(int[] num) {//先对数组进行排序Arrays.sort(num);List<List<Integer>> res = new ArrayList<>();for (int i = 0; i < num.length - 2; i++) {// 这一轮固定位如果和之前固定的一样那就没必要再找一遍了if (i > 0 && num[i] == num[i - 1])continue;//因为是排序的,如果第一个数字大于0,那么后面的也都//大于0,他们三个数字的和不可能等于0if (num[i] > 0)break;int left = i + 1;//左指针int right = num.length - 1;//右指针int target = -num[i];while (left < right) {//左右指针的和int sum = num[left] + num[right];if (sum == target) {//找到了一组,把他们加入到集合list中res.add(Arrays.asList(num[i], num[left], num[right]));// 如果有重复的值就一次性移动到其他值,而不是每一轮固定移动一步while (left < right && num[left] == num[left + 1])left++;while (left < right && num[right] == num[right - 1])right--;left++;right--;} else if (sum < target) {left++;} else {right--;}}}return res;
}
相关文章:

从零学算法15
15.给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元组。 示例 …...

《Effective C++》条款27
尽量少做转型动作 class A { public:A(int x) :a(x) {};virtual void add(){a;} private:int a; }; class B :public A { public:B(int x) :b(x),A(x) {};virtual void add(){static_cast<A>(*this).add();b;}private:int b; }; 如上描述把子类转型为A类,调用…...

无图谱不AI之三元组数据保存Neo4j
目录 1. 代码学习1.1 源代码1.2 代码解读 没有图谱称为弱人工智能,有图谱的称为强人工智能。 图谱可以让机器学习和人工智能具备推理能力。 1. 代码学习 1.1 源代码 # -*- coding: utf-8 -*- from py2neo import Node, Graph, Relationship# 可以先阅读下文档&a…...
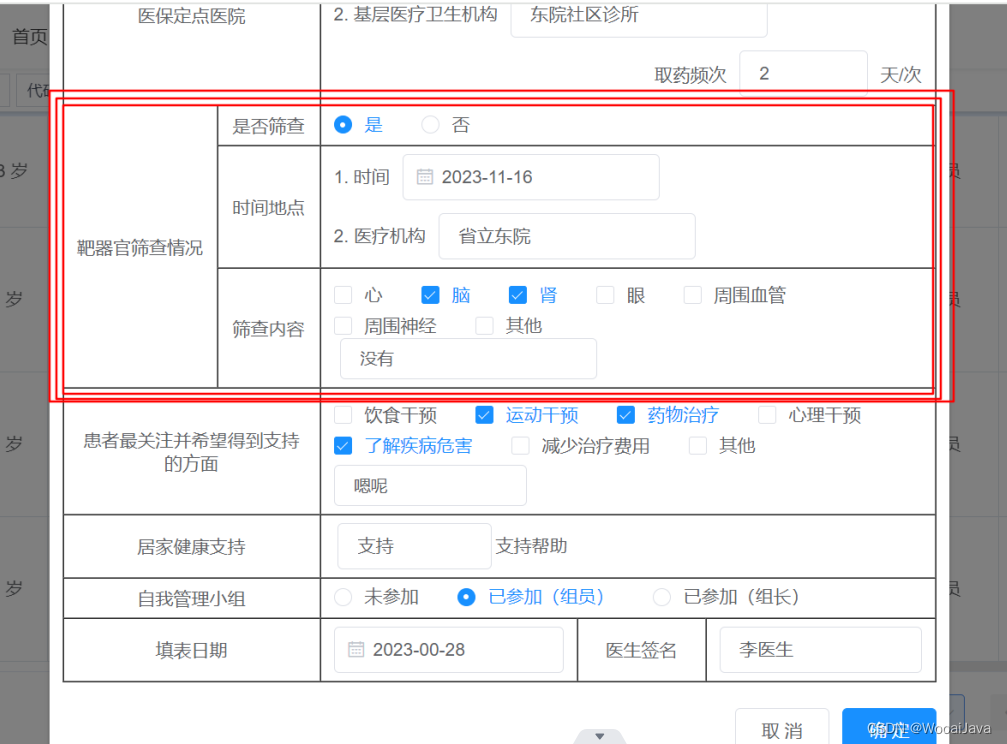
Mybatisplus同时向两张表里插入数据[事务的一致性]
一、需求:把靶器官的数据,单独拿出来作为一个从表,以List的方式接收这段数据; 此时分析,是需要有两个实体的,一个是主表的实体,一个是从表的实体,并在主表实体新增一个List 字段来接…...

天眼销:精准的企业名录
企业名录的重要性,对于销售而言都是极其重要的。本期为家人们分享如何正确挑选出优质的企业名录渠道,避免走一些弯弯坑坑。 为了有效利用企业名录进行客户开发,您需要关注信息的准确性、可提供的资源数量以及信息的时效性。能否根据您的需求…...
)
TypeError: Cannot read properties of null (reading ‘shapeFlag‘)
vue3 开发过程遇到这样一个报错 TypeError: Cannot read properties of null (reading shapeFlag)最后发现是ref定义的变量,在访问时没有使用.valuereactive 变量初始化是数组,如果使用字符串赋值时也会报这个错。...
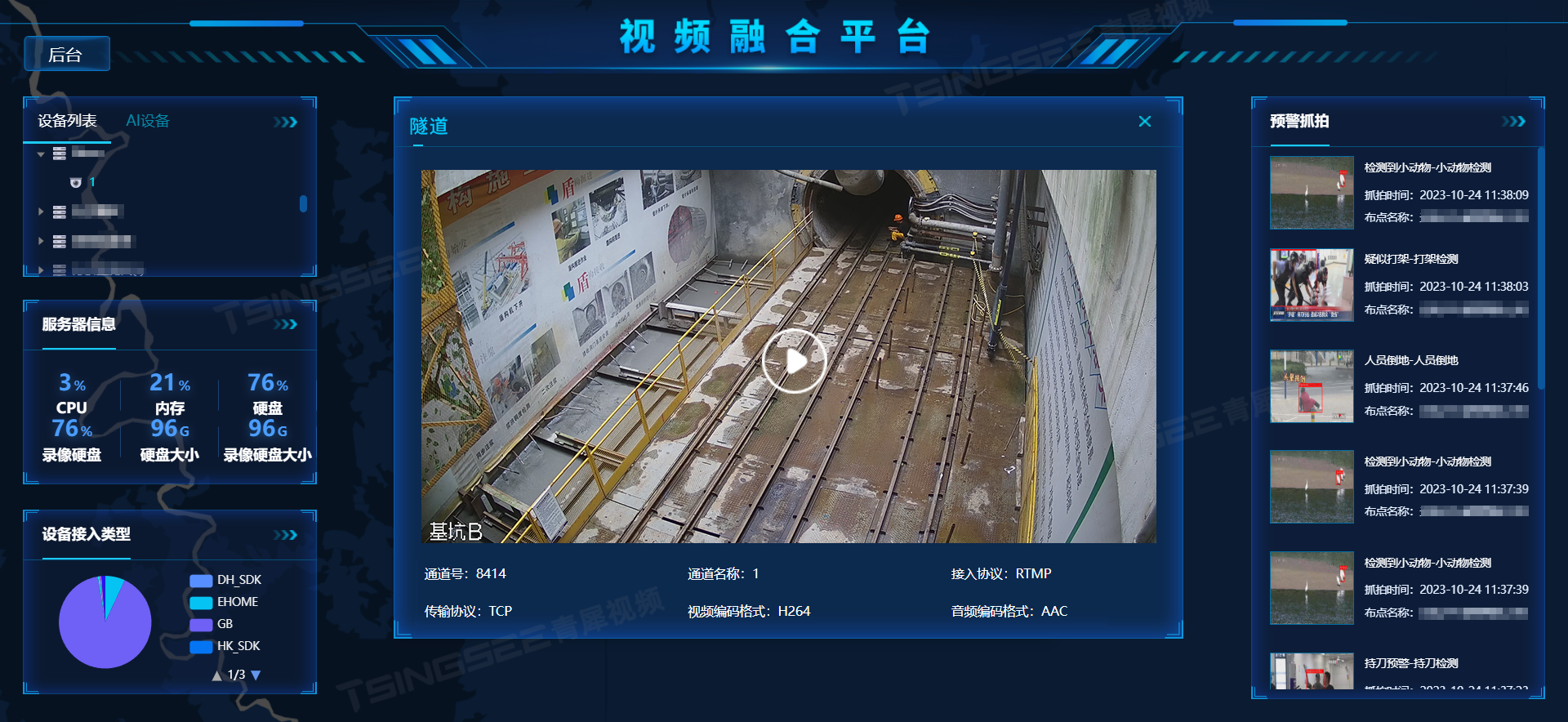
视频监控平台EasyCVR多场景应用,AI视频分析技术助力行业升级转型
传统的视频监控系统建设,经常存在各方面的因素制约,造成管理机制不健全、统筹规划不到位、联网共享不规范,形成“信息孤岛”、“数据烟囱”。在监控系统的建设中缺乏统一规划,标准不统一、视频图像信息利用率低等问题日益突出。随…...
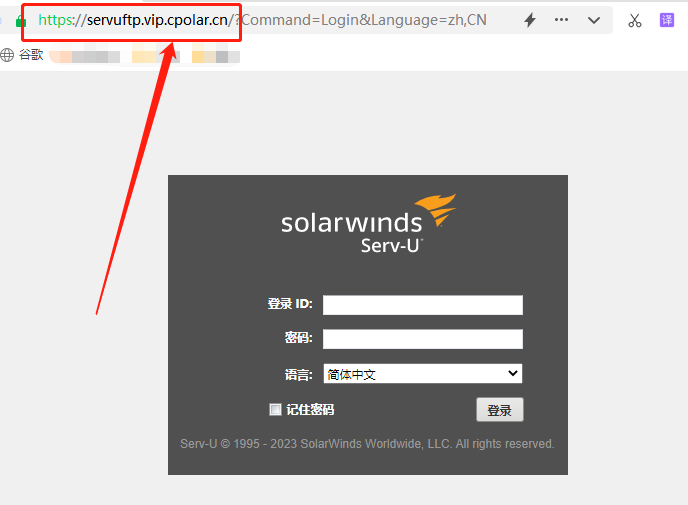
如何搭建外网可访问的Serv-U FTP服务器,轻松远程共享文件!
目录 1. 前言 2. 本地FTP搭建 2.1 Serv-U下载和安装 2.2 Serv-U共享网页测试 2.3 Cpolar下载和安装 3. 本地FTP发布 3.1 Cpolar云端设置 3.2 Cpolar本地设置 4. 公网访问测试 5. 总结 1. 前言 科技日益发展的今天,移动电子设备似乎成了我们生活的主角&am…...

c++--类型的基础
1.常量对象,常量成员函数 (1).常量对象 常量对象的引用和指针不能调用类的普通的成员函数。只能调用常量成员函数。 (2).常量成员函数:把const放在类成员函数参数列表后。表示隐含的this是一个指向常量的指针 (3).当创建一个const对象时,直到…...

Python with提前退出:坑与解决方案
Python with提前退出:坑与解决方案 问题的起源 早些时候使用with实现了一版全局进程锁,希望实现以下效果: Python with提前退出:坑与解决方案 全局进程锁本身不用多说,大部分都依靠外部的缓存来实现的,r…...
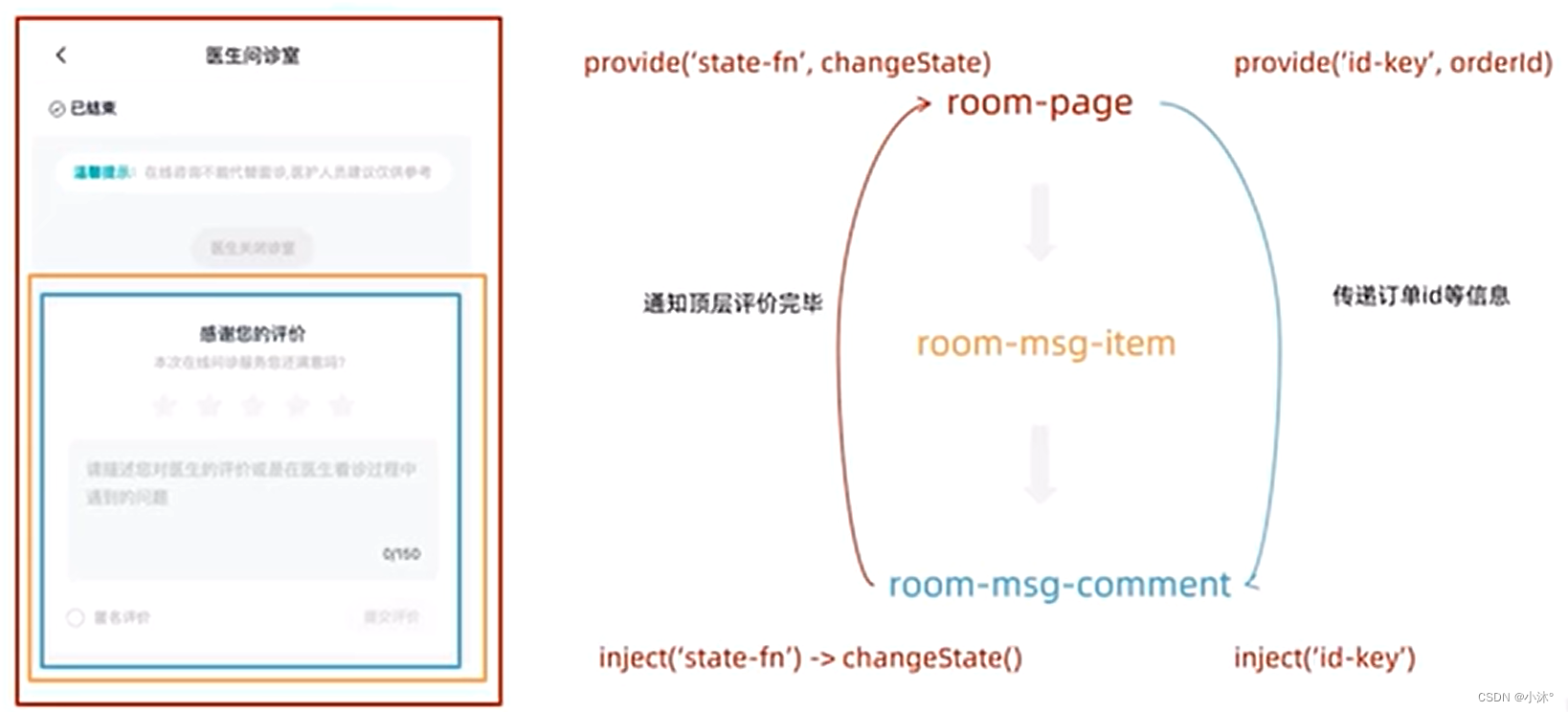
Vue3-provide和inject
作用和场景:顶层组件向任意的底层组件传递数据和方法,实现跨层组件通信 跨层传递普通数据: 1.顶层组件通过provide函数提供数据 2.底层组件通过inject函数获取数据 既可以传递普通数据,也可以使用ref传递响应式数据(…...

Python与设计模式--适配器模式
23种计模式之 前言 (5)单例模式、工厂模式、简单工厂模式、抽象工厂模式、建造者模式、原型模式、(7)代理模式、装饰器模式、适配器模式、门面模式、组合模式、享元模式、桥梁模式、(11)策略模式、责任链模式、命令模式、中介者模…...
大模型能否生成搜索引擎的未来?
文|郝 鑫 编|刘雨琦 ChatGPT火爆之前,水面下,也有中国公司也在朝着智能助手的方向努力。夸克便是其中之一。在GPT风靡科技圈后,国内就开始陆续冒出一些大模型厂商。对当时夸克而言,做大模型毋庸置疑&am…...

鸿蒙开发-ArkTS 语言-状态管理
[写在前面: 文章多处用到gif动图,如未自动播放,请点击图片] 衔接上一篇:鸿蒙开发-ArkTS 语言-基础语法 3. 状态管理 变量必须被装饰器装饰才能成为状态变量,状态变量的改变才能导致 UI 界面重新渲染 概念描述状态变量被状态装饰器装饰的变…...

一篇文章带你掌握MongoDB
文章目录 1. 前言2. MongoDB简介3. MongoDB与关系型数据库的对比4. MongoDB的安装5. Compass的使用6. MongoDB的常用语句7. 总结 1. 前言 本文旨在帮助大家快速了解MongoDB,快速了解和掌握MongoDB的干货内容. 2. MongoDB简介 MongoDB是一种NoSQL数据库,采用了文档…...

删除docker镜像
随着我们拉取的镜像越来越多,镜像的管理越来越难。这时候可能就需要删除镜像了。 本关的任务是学习如何删除容器,要求学习者参照示例,将busybox:latest镜像删除。 相关知识 删除镜像 如果要删除本地的镜像,可以使用 docker rm…...
力扣 --- 删除有序数组中的重复项 II
题目描述: 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的…...

Opencv图像处理(全)
文章目录 博主精品专栏导航备注:以下源码均可运行,不同项目涉及的函数均有详细分析说明。11、图像项目实战(一)银行卡号识别 —— sort_contours()、resize()(二)文档扫描OCR识别 —— cv2.getPerspectiveT…...
Flutter桌面应用开发之毛玻璃效果
目录 效果实现方案依赖库支持平台实现步骤注意事项话题扩展 毛玻璃效果:毛玻璃效果是一种模糊化的视觉效果,常用于图像处理和界面设计中。它可以通过在图像或界面元素上应用高斯模糊来实现。使用毛玻璃效果可以增加图像或界面元素的柔和感,同…...
基于C#实现优先队列
一、堆结构 1.1性质 堆是一种很松散的序结构树,只保存了父节点和孩子节点的大小关系,并不规定左右孩子的大小,不像排序树那样严格,又因为堆是一种完全二叉树,设节点为 i,则 i/2 是 i 的父节点,2i 是 i 的…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
