基于C#实现优先队列
一、堆结构
1.1性质
堆是一种很松散的序结构树,只保存了父节点和孩子节点的大小关系,并不规定左右孩子的大小,不像排序树那样严格,又因为堆是一种完全二叉树,设节点为 i,则 i/2 是 i 的父节点,2i 是 i 的左孩子,2i+1 是 i 的右孩子,所以在实现方式上可以采用轻量级的数组。

1.2用途
如果大家玩过微软的 MSMQ 的话,我们发现它其实也是一个优先队列,还有刚才说的抓取 url,不过很遗憾,为什么.net 类库中没有优先队列,而 java1.5 中就已经支持了。
1.3实现
<1> 堆结构节点定义:
我们在每个节点上定义一个level,表示该节点的优先级,也是构建堆时采取的依据。
/// <summary>/// 定义一个数组来存放节点/// </summary>private List<HeapNode> nodeList = new List<HeapNode>();#region 堆节点定义/// <summary>/// 堆节点定义/// </summary>public class HeapNode{/// <summary>/// 实体数据/// </summary>public T t { get; set; }/// <summary>/// 优先级别 1-10个级别 (优先级别递增)/// </summary>public int level { get; set; }public HeapNode(T t, int level){this.t = t;this.level = level;}public HeapNode() { }}#endregion
<2> 入队操作
入队操作时我们要注意几个问题:
①:完全二叉树的构建操作是“从上到下,从左到右”的形式,所以入队的节点是放在数组的最后,也就是树中叶子层的有序最右边空位。
②:当节点插入到最后时,有可能破坏了堆的性质,此时我们要进行“上滤操作”,当然时间复杂度为 O(lgN)。
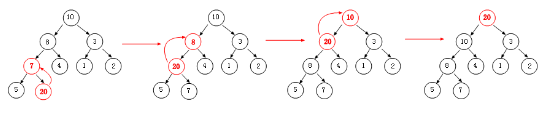
当我将节点“20”插入到堆尾的时候,此时破坏了堆的性质,从图中我们可以清楚的看到节点“20”的整个上滤过程,有意思吧,还有一点就是:获取插入节点的父亲节点的算法是:parent=list.count/2-1。这也得益于完全二叉树的特性。
#region 添加操作/// <summary>/// 添加操作/// </summary>public void Eequeue(T t, int level = 1){//将当前节点追加到堆尾nodeList.Add(new HeapNode(t, level));//如果只有一个节点,则不需要进行筛操作if (nodeList.Count == 1)return;//获取最后一个非叶子节点int parent = nodeList.Count / 2 - 1;//堆调整UpHeapAdjust(nodeList, parent);}#endregion#region 对堆进行上滤操作,使得满足堆性质/// <summary>/// 对堆进行上滤操作,使得满足堆性质/// </summary>/// <param name="nodeList"></param>/// <param name="index">非叶子节点的之后指针(这里要注意:我们/// 的筛操作时针对非叶节点的)/// </param>public void UpHeapAdjust(List<HeapNode> nodeList, int parent){while (parent >= 0){//当前index节点的左孩子var left = 2 * parent + 1;//当前index节点的右孩子var right = left + 1;//parent子节点中最大的孩子节点,方便于parent进行比较//默认为left节点var max = left;//判断当前节点是否有右孩子if (right < nodeList.Count){//判断parent要比较的最大子节点max = nodeList[left].level < nodeList[right].level ? right : left;}//如果parent节点小于它的某个子节点的话,此时筛操作if (nodeList[parent].level < nodeList[max].level){//子节点和父节点进行交换操作var temp = nodeList[parent];nodeList[parent] = nodeList[max];nodeList[max] = temp;//继续进行更上一层的过滤parent = (int)Math.Ceiling(parent / 2d) - 1;}else{break;}}}#endregion
<3> 出队操作
从图中我们可以看出,优先级最大的节点会在一阵痉挛后上升到堆顶,出队操作时,我们采取的方案是:弹出堆顶元素,然后将叶子层中的最右子节点赋给堆顶,同样这时也会可能存在破坏堆的性质,最后我们要被迫进行下滤操作。
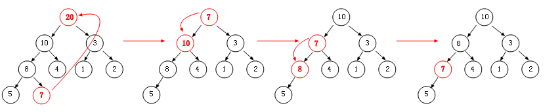
我图中可以看出:首先将堆顶 20 弹出,然后将 7 赋给堆顶,此时堆性质遭到破坏,最后我们清楚的看到节点 7 的下滤过程,从摊还分析的角度上来说,下滤的层数不超过 2-3 层,所以整体上来说出队的时间复杂度为一个常量 O(1)。
#region 优先队列的出队操作/// <summary>/// 优先队列的出队操作/// </summary>/// <returns></returns>public HeapNode Dequeue(){if (nodeList.Count == 0)return null;//出队列操作,弹出数据头元素var pop = nodeList[0];//用尾元素填充头元素nodeList[0] = nodeList[nodeList.Count - 1];//删除尾节点nodeList.RemoveAt(nodeList.Count - 1);//然后从根节点下滤堆DownHeapAdjust(nodeList, 0);return pop;}#endregion#region 对堆进行下滤操作,使得满足堆性质/// <summary>/// 对堆进行下滤操作,使得满足堆性质/// </summary>/// <param name="nodeList"></param>/// <param name="index">非叶子节点的之后指针(这里要注意:我们/// 的筛操作时针对非叶节点的)/// </param>public void DownHeapAdjust(List<HeapNode> nodeList, int parent){while (2 * parent + 1 < nodeList.Count){//当前index节点的左孩子var left = 2 * parent + 1;//当前index节点的右孩子var right = left + 1;//parent子节点中最大的孩子节点,方便于parent进行比较//默认为left节点var max = left;//判断当前节点是否有右孩子if (right < nodeList.Count){//判断parent要比较的最大子节点max = nodeList[left].level < nodeList[right].level ? right : left;}//如果parent节点小于它的某个子节点的话,此时筛操作if (nodeList[parent].level < nodeList[max].level){//子节点和父节点进行交换操作var temp = nodeList[parent];nodeList[parent] = nodeList[max];nodeList[max] = temp;//继续进行更下一层的过滤parent = max;}else{break;}}}#endregion
相关文章:

基于C#实现优先队列
一、堆结构 1.1性质 堆是一种很松散的序结构树,只保存了父节点和孩子节点的大小关系,并不规定左右孩子的大小,不像排序树那样严格,又因为堆是一种完全二叉树,设节点为 i,则 i/2 是 i 的父节点,2i 是 i 的…...
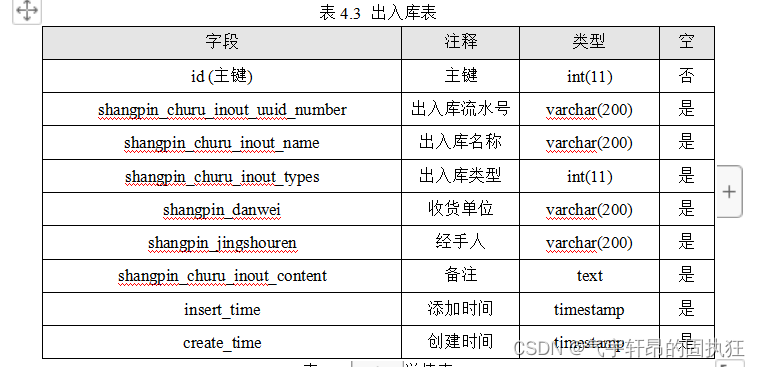
ssm+vue的仓库在线管理系统的设计与实现(有报告)。Javaee项目,ssm vue前后端分离项目。
演示视频: ssmvue的仓库在线管理系统的设计与实现(有报告)。Javaee项目,ssm vue前后端分离项目。 项目介绍: 采用M(model)V(view)C(controller)三…...

什么是木马
木马 1. 定义2. 木马的特征3. 木马攻击流程4. 常见木马类型5. 如何防御木马 1. 定义 木马一名来源于古希腊特洛伊战争中著名的“木马计”,指可以非法控制计算机,或在他人计算机中从事秘密活动的恶意软件。 木马通过伪装成正常软件被下载到用户主机&…...

Pinia仓库统一管理
pinia独立维护 在src/stores文件夹下创建index.js文件,将main.js中关于pinia的语句放到index.js中 index.js文件内容: import { createPinia } from pinia import piniaPluginPersistedstate from pinia-plugin-persistedstate const pinia createPi…...
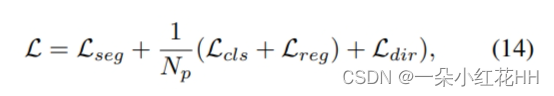
[论文阅读]VoxSet——Voxel Set Transformer
VoxSet Voxel Set Transformer: A Set-to-Set Approach to 3D Object Detection from Point Clouds 论文网址:VoxSet 论文代码:VoxSet 简读论文 这篇论文提出了一个称为Voxel Set Transformer(VoxSeT)的3D目标检测模型,主要有以下几个亮点: 提出了基于…...

【开源】基于Vue.js的医院门诊预约挂号系统的设计和实现
项目编号: S 033 ,文末获取源码。 \color{red}{项目编号:S033,文末获取源码。} 项目编号:S033,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 功能性需求2.1.1 数据中心模块2.1.2…...
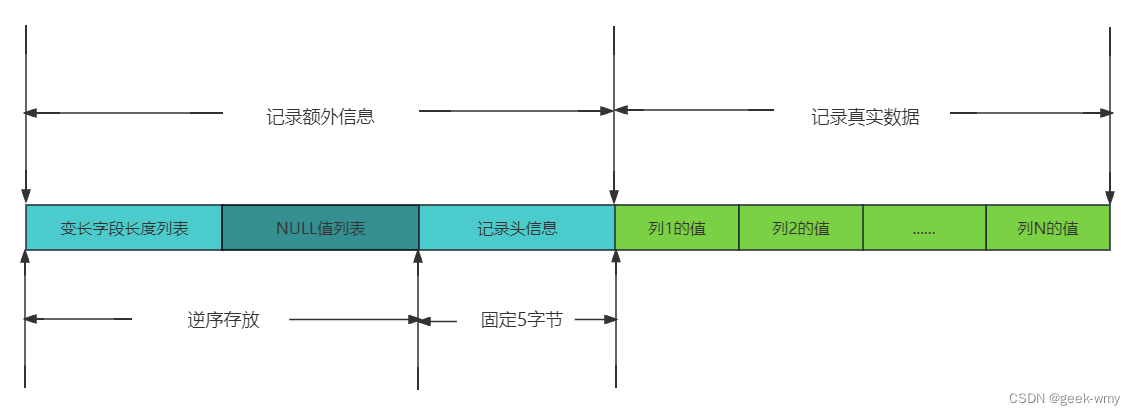
1、Mysql架构与历史
Mysql逻辑架构 最上层是服务并不是Mysql所独有的,大多数基于网络的客户端/服务器的工具或者服务都有类似的架构,比如连接处理,授权认证,安全等。 第二层是Mysql比较有意思的部分。大多数Mysql的核心服务都在这一层,…...
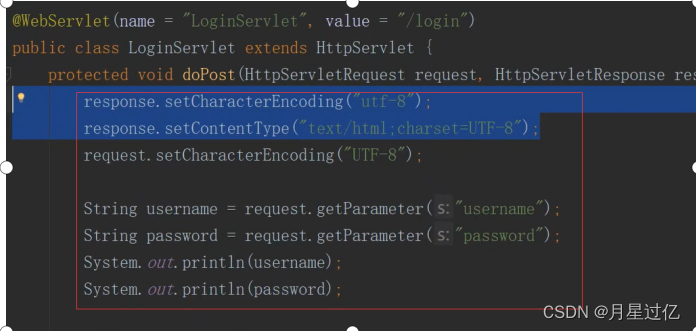
考试复习
选择20道 填空10道 判断10道 简答4-5道 编程题2道 一、选择题 1.js中更改一个input框的值: <input ida type"text" value"123456"> 通过a.value改变他的值 方法: 在script标签中通过id获得该输入框对象,然…...

使用Docker一键安装MySQL与Nginx脚本
在项目开发和部署过程中,使用Docker可以方便地快速搭建和管理数据库(MySQL)以及Web服务器(Nginx)。本教程将为你提供一份一键安装脚本。 安装Docker 首先,确保你的系统已经安装了Docker。如果没有安装&am…...

VMware系列:Vmware vSphere常见问题及解决办法
Vmware vSphere常见问题及解决办法 1. 虚拟机文件被锁,无法正常 power on故障状态:祸根:解决方法:2. 忽视掉ESXi/vCenter Server提示SSH事件的方法3. 尝试迁移一台带USB设备的VM失败故障状态:故障分析:解决方案:4. Convert Linux系统的Troublshooting过程5. vCenter Serv…...
基于web宠颐生宠物医院系统设计与实现
基于web宠颐生医院系统开发与实现 摘要:时代飞速发展,网络也飞速发展,互联网许多的行业都可以用互联网实现了,互联网已经成为了人们生活中重要的一部分,或多或少的影响着我们的生活,互联网在给我带了方便的…...
二、Gitee使用方法
目录 (1)首先可以注册一个 gitee 账号,注册很方便,自行注册 (2)登陆后进入你的主页 (3)创建仓库 (3)克隆 (4)代码提交 …...

【C++】string模拟
string讲解:【C】String类-CSDN博客 基本框架 #pragma once #include <iostream> using namespace std; namespace wzf {class string{public:// 默认构造函数string(): _str(new char[1]), _size(0), _capacity(0){_str[0] \0; // 在没有内容时仍要有终…...

python高级练习题库实验1(A)部分
文章目录 题目1代码实验结果题目2代码实验结果题目3代码实验结果题目4代码实验结果题目总结题目1 输入一个整数,用于控制输出*的个数,输入日期,按照特定格式输出 研究下面的例子,并编写一个与这些例子完全相同的程序。 代码 import datetime# ask user for length of b…...

数据库应用:MongoDB 数据备份与恢复
目录 一、实验 1.MongoDB 数据库备份与恢复 2.MongoDB 数据表备份与恢复 二、问题 1.MongoDB有哪些命令行工具实现数据备份与恢复 一、实验 1.MongoDB 数据库备份与恢复 (1)查看版本 rootnode1:~# mongo --version(2)准备…...
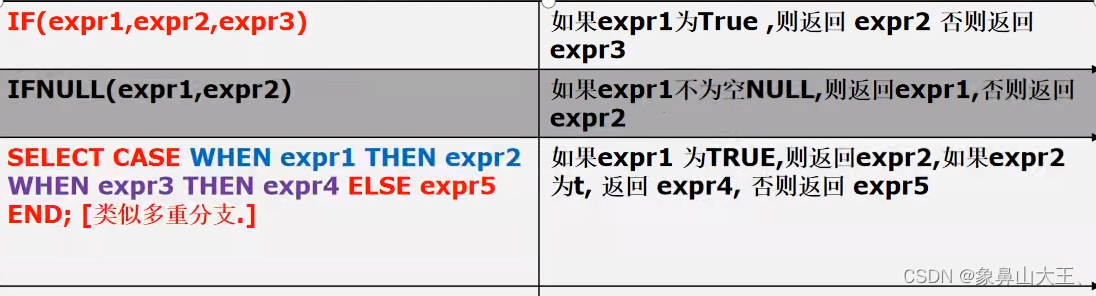
MySQL-函数
一、统计函数 CREATE TABLE student (id INT NOT NULL DEFAULT 1,name varchar(20) not null default ,chinese float not null default 0.0,english float not null default 0.0,math float not null default 0.0 );insert into student values (1,曹操,77,89,85);insert int…...
)
【12】Python函数专题(下)
文章目录 1. 高阶函数1.1 以函数为参数1.2 以函数为返回值1.3 以函数为 参数和返回值2. 闭包3. 装饰器3.1 装饰器的引入3.2. 装饰器的使用3.3 装饰器强化练习🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔…...
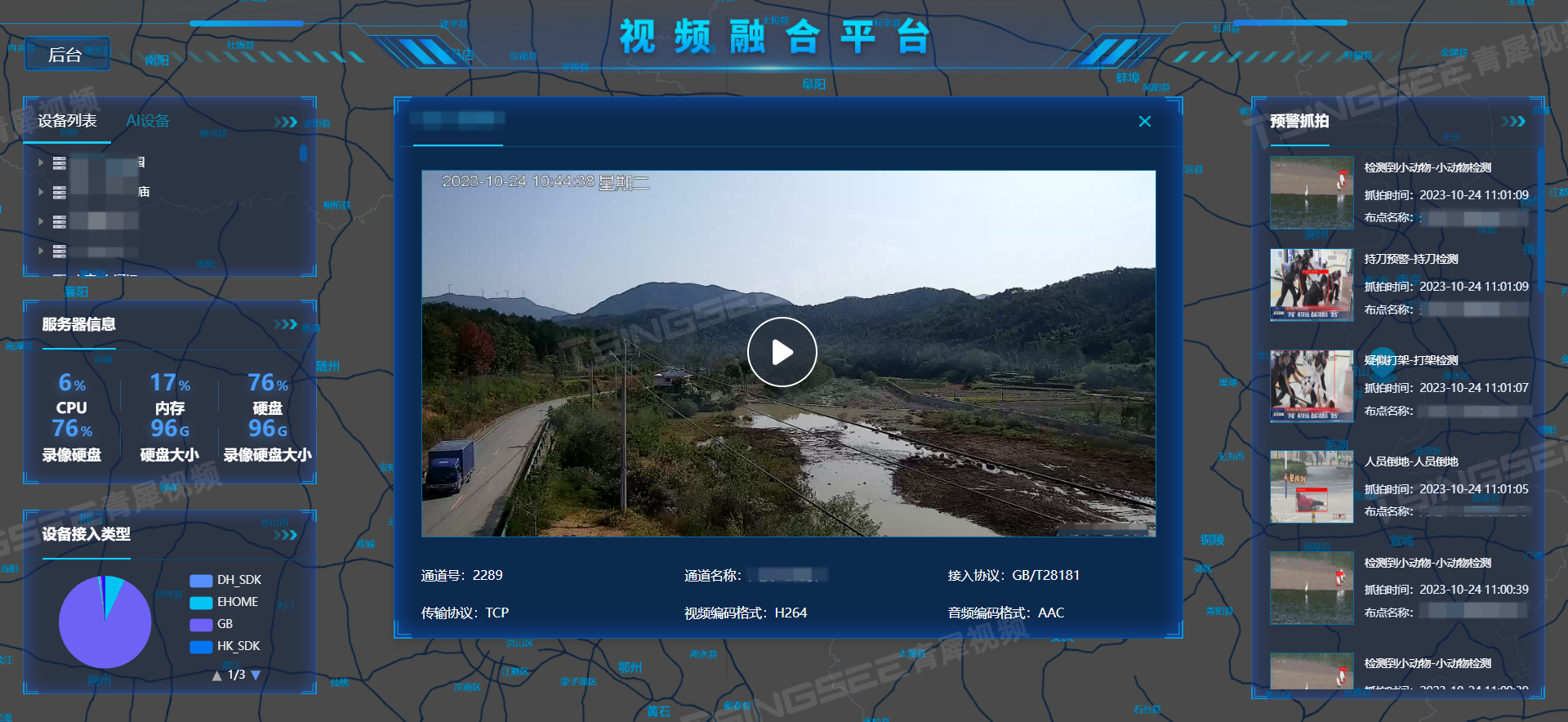
国标GB28181协议/RTSP视频监控汇聚平台EasyCVR(V.3.4)页面UI大更新
为提高用户体验,增强平台功能,旭帆科技的Easy系列平台也在不断优化更新中。在最新的EasyCVR(V.3.4)中,其最显著的区别即为首页UI的调整。 其亮点是在【配置中心】-【基础配置】-【展示信息】中,首页UI可分…...
生成式AI与预测式AI的主要区别与实际应用
近年来,预测式人工智能(Predictive AI)通过先进的推荐算法、风险评估模型、以及欺诈检测工具,一直在推高着该领域公司的投资回报率。然而,今年初突然杀出的生成式人工智能(Generative AI)突然成…...

【JavaEE】多线程 -- 死锁问题
目录 1. 问题引入 2.死锁问题的概念和原因 3. 解决死锁问题 1. 问题引入 在学习死锁之前, 我们先观察下面的代码能否输出正确的结果: 运行程序, 能正常输出结果: 这个代码只管上看起来, 好像是有锁冲突的, 此时的 locker 对象已经是加锁的状态, 在尝试对 locker 加锁, 不应该…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
