Vue3-provide和inject
作用和场景:顶层组件向任意的底层组件传递数据和方法,实现跨层组件通信
跨层传递普通数据:
1.顶层组件通过provide函数提供数据
2.底层组件通过inject函数获取数据
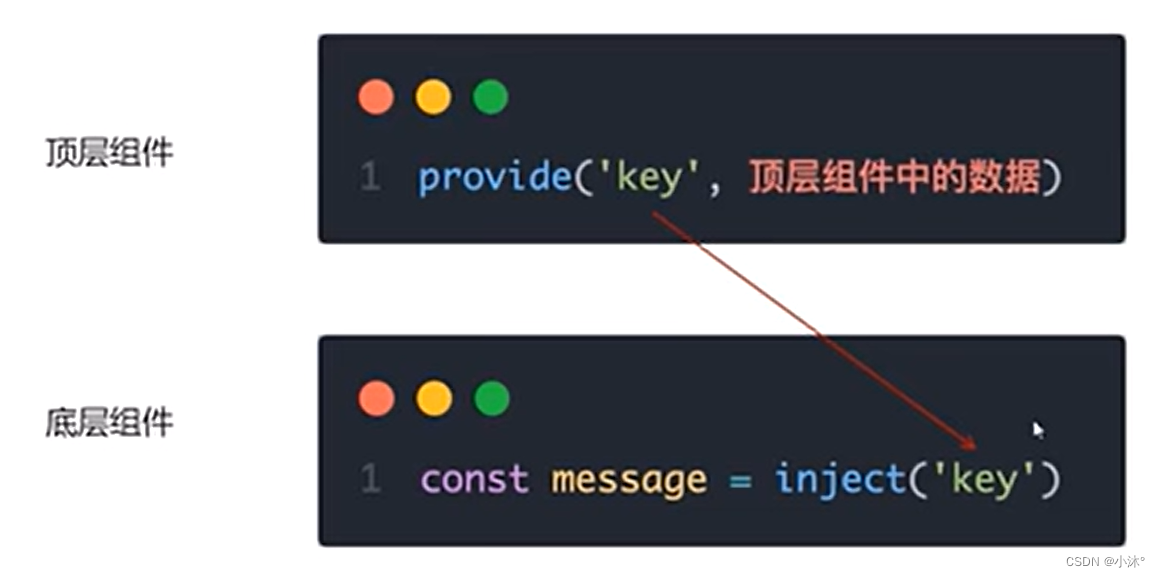
既可以传递普通数据,也可以使用ref传递响应式数据(顶层组件修改数据后可以响应过去)

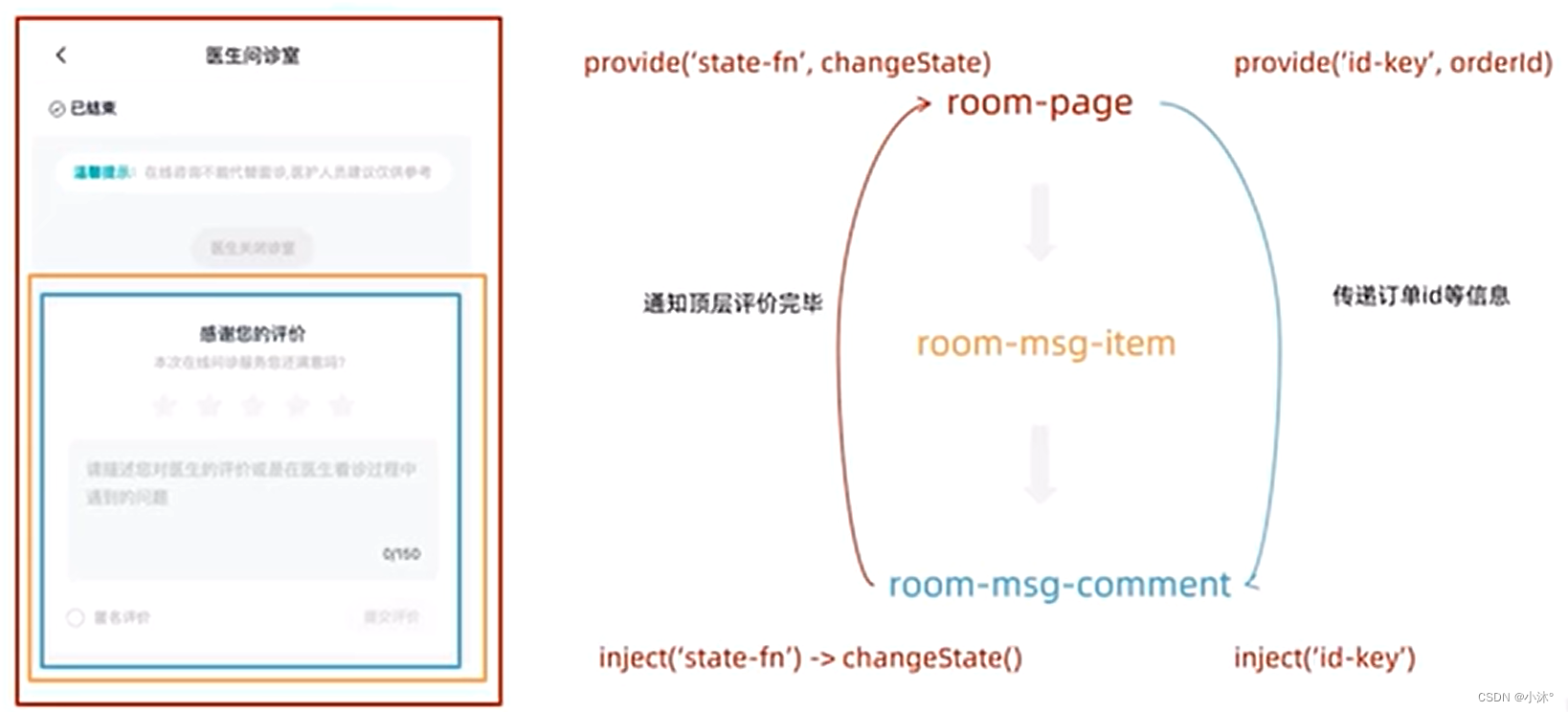
但是底层组件不能修改顶层组件传递过来的数据,所以我们可以在顶层组件中跨层传递函数,给子孙后代传递可以修改数据的方法

顶层组件
<script setup>import {provide,ref} from 'vue'const count=ref(100)provide('changeCount',(newCount)=>{count.value=newCount})
</script>底层组件
<script setup>import {inject} from 'vue'const changeCount=inject(changeCount)changeCount(1000)//可以放在点击事件上
</script>这样就可以把父组件里的count改为1000了
相关文章:

Vue3-provide和inject
作用和场景:顶层组件向任意的底层组件传递数据和方法,实现跨层组件通信 跨层传递普通数据: 1.顶层组件通过provide函数提供数据 2.底层组件通过inject函数获取数据 既可以传递普通数据,也可以使用ref传递响应式数据(…...

Python与设计模式--适配器模式
23种计模式之 前言 (5)单例模式、工厂模式、简单工厂模式、抽象工厂模式、建造者模式、原型模式、(7)代理模式、装饰器模式、适配器模式、门面模式、组合模式、享元模式、桥梁模式、(11)策略模式、责任链模式、命令模式、中介者模…...
大模型能否生成搜索引擎的未来?
文|郝 鑫 编|刘雨琦 ChatGPT火爆之前,水面下,也有中国公司也在朝着智能助手的方向努力。夸克便是其中之一。在GPT风靡科技圈后,国内就开始陆续冒出一些大模型厂商。对当时夸克而言,做大模型毋庸置疑&am…...

鸿蒙开发-ArkTS 语言-状态管理
[写在前面: 文章多处用到gif动图,如未自动播放,请点击图片] 衔接上一篇:鸿蒙开发-ArkTS 语言-基础语法 3. 状态管理 变量必须被装饰器装饰才能成为状态变量,状态变量的改变才能导致 UI 界面重新渲染 概念描述状态变量被状态装饰器装饰的变…...

一篇文章带你掌握MongoDB
文章目录 1. 前言2. MongoDB简介3. MongoDB与关系型数据库的对比4. MongoDB的安装5. Compass的使用6. MongoDB的常用语句7. 总结 1. 前言 本文旨在帮助大家快速了解MongoDB,快速了解和掌握MongoDB的干货内容. 2. MongoDB简介 MongoDB是一种NoSQL数据库,采用了文档…...

删除docker镜像
随着我们拉取的镜像越来越多,镜像的管理越来越难。这时候可能就需要删除镜像了。 本关的任务是学习如何删除容器,要求学习者参照示例,将busybox:latest镜像删除。 相关知识 删除镜像 如果要删除本地的镜像,可以使用 docker rm…...
力扣 --- 删除有序数组中的重复项 II
题目描述: 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。 不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的…...

Opencv图像处理(全)
文章目录 博主精品专栏导航备注:以下源码均可运行,不同项目涉及的函数均有详细分析说明。11、图像项目实战(一)银行卡号识别 —— sort_contours()、resize()(二)文档扫描OCR识别 —— cv2.getPerspectiveT…...
Flutter桌面应用开发之毛玻璃效果
目录 效果实现方案依赖库支持平台实现步骤注意事项话题扩展 毛玻璃效果:毛玻璃效果是一种模糊化的视觉效果,常用于图像处理和界面设计中。它可以通过在图像或界面元素上应用高斯模糊来实现。使用毛玻璃效果可以增加图像或界面元素的柔和感,同…...
基于C#实现优先队列
一、堆结构 1.1性质 堆是一种很松散的序结构树,只保存了父节点和孩子节点的大小关系,并不规定左右孩子的大小,不像排序树那样严格,又因为堆是一种完全二叉树,设节点为 i,则 i/2 是 i 的父节点,2i 是 i 的…...
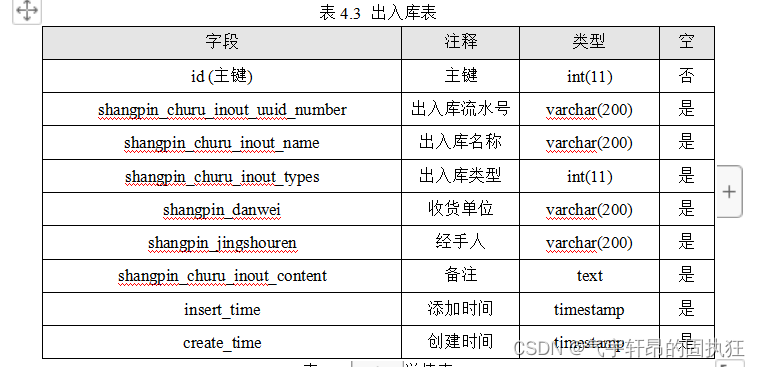
ssm+vue的仓库在线管理系统的设计与实现(有报告)。Javaee项目,ssm vue前后端分离项目。
演示视频: ssmvue的仓库在线管理系统的设计与实现(有报告)。Javaee项目,ssm vue前后端分离项目。 项目介绍: 采用M(model)V(view)C(controller)三…...

什么是木马
木马 1. 定义2. 木马的特征3. 木马攻击流程4. 常见木马类型5. 如何防御木马 1. 定义 木马一名来源于古希腊特洛伊战争中著名的“木马计”,指可以非法控制计算机,或在他人计算机中从事秘密活动的恶意软件。 木马通过伪装成正常软件被下载到用户主机&…...

Pinia仓库统一管理
pinia独立维护 在src/stores文件夹下创建index.js文件,将main.js中关于pinia的语句放到index.js中 index.js文件内容: import { createPinia } from pinia import piniaPluginPersistedstate from pinia-plugin-persistedstate const pinia createPi…...
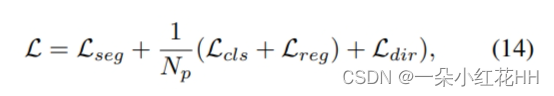
[论文阅读]VoxSet——Voxel Set Transformer
VoxSet Voxel Set Transformer: A Set-to-Set Approach to 3D Object Detection from Point Clouds 论文网址:VoxSet 论文代码:VoxSet 简读论文 这篇论文提出了一个称为Voxel Set Transformer(VoxSeT)的3D目标检测模型,主要有以下几个亮点: 提出了基于…...

【开源】基于Vue.js的医院门诊预约挂号系统的设计和实现
项目编号: S 033 ,文末获取源码。 \color{red}{项目编号:S033,文末获取源码。} 项目编号:S033,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 功能性需求2.1.1 数据中心模块2.1.2…...
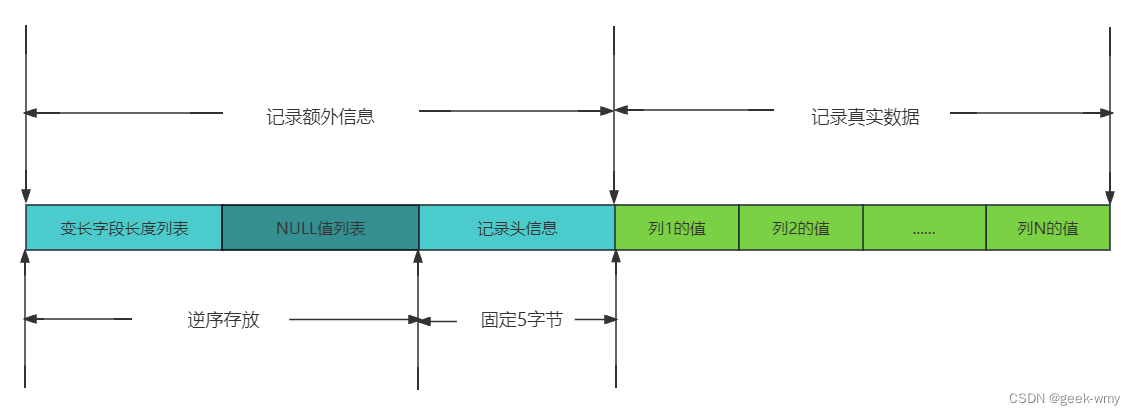
1、Mysql架构与历史
Mysql逻辑架构 最上层是服务并不是Mysql所独有的,大多数基于网络的客户端/服务器的工具或者服务都有类似的架构,比如连接处理,授权认证,安全等。 第二层是Mysql比较有意思的部分。大多数Mysql的核心服务都在这一层,…...
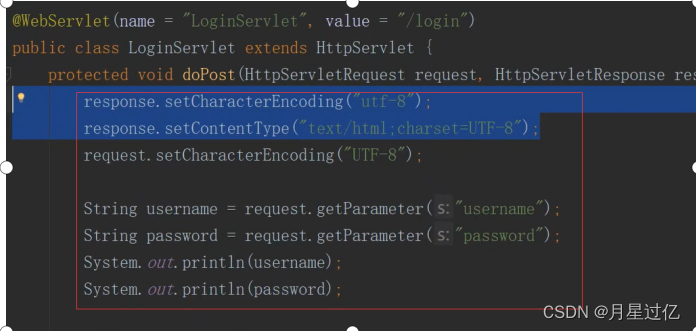
考试复习
选择20道 填空10道 判断10道 简答4-5道 编程题2道 一、选择题 1.js中更改一个input框的值: <input ida type"text" value"123456"> 通过a.value改变他的值 方法: 在script标签中通过id获得该输入框对象,然…...

使用Docker一键安装MySQL与Nginx脚本
在项目开发和部署过程中,使用Docker可以方便地快速搭建和管理数据库(MySQL)以及Web服务器(Nginx)。本教程将为你提供一份一键安装脚本。 安装Docker 首先,确保你的系统已经安装了Docker。如果没有安装&am…...

VMware系列:Vmware vSphere常见问题及解决办法
Vmware vSphere常见问题及解决办法 1. 虚拟机文件被锁,无法正常 power on故障状态:祸根:解决方法:2. 忽视掉ESXi/vCenter Server提示SSH事件的方法3. 尝试迁移一台带USB设备的VM失败故障状态:故障分析:解决方案:4. Convert Linux系统的Troublshooting过程5. vCenter Serv…...
基于web宠颐生宠物医院系统设计与实现
基于web宠颐生医院系统开发与实现 摘要:时代飞速发展,网络也飞速发展,互联网许多的行业都可以用互联网实现了,互联网已经成为了人们生活中重要的一部分,或多或少的影响着我们的生活,互联网在给我带了方便的…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
