数值分析总结
数值分析总结思维导图
Docs
相关代码的使用和注释
列主元Gauss消元法
%%列主元高斯消元法
function x=Gauss_lzy(A,b)%A为方程组系数矩阵,b为方程组的右侧向量,x为方程组的解
[n,m]=size(A);%%得到矩阵A的行和列的宽度
nb=length(b);%%方程组右侧向量的长度
if n~=m%%如果系数矩阵的行数和方程组右侧向量的长度不相等,错误error('%系数矩阵必须是方的');
end
if m~=nb%%方程的变量数和方程右侧向量的长度不相等,错误error('%b的维数与方程的行数不匹配!');
end
for k=1:n-1%%执行n-1次选主元的过程,就可以选完所有,最后剩下的一个直接处理,也表示列%选主元a_max=0;%%先定义一个最大值for i=k:n%%从当前行开始到最后一行选主元if abs(A(i,k))>a_max%%如果遇到比当前最大值大的直接记录作为主元a_max=abs(A(i,k));r=i;%%同时记录下它的行数endendif a_max<1e-15%%如果记录的主元小于1e-5,错误error('%系数矩阵奇异,无法匹配方程组');end%交换两行if r>k%%如果主元所在的行不是当前行,需要交换左侧和右侧for j=k:nz=A(k,j);A(k,j)=A(r,j);A(r,j)=z;endz=b(k);b(k)=b(r);b(r)=z;end%消元过程for i=k+1:n%%从当前行的下一行开始消元m=A(i,k)/A(k,k);for j=k+1:nA(i,j)=A(i,j)-m*A(k,j);endb(i)=b(i)-m*b(k);end
end
%回代过程
if abs(A(n,n))<1e-15error('%系数矩阵奇异,无法求解方程组');
end
x=zeros(size(b));
for k=n:-1:1%%从最后一行开始回代for j=k+1:nb(k)=b(k)-A(k,j)*x(j);endx(k)=b(k)/A(k,k);
end
Jacobi迭代法
%%Jacobi迭代法
function x=Jacobi(A,b,x0,eps)
D=diag(diag(A));%%将矩阵A的对角元素提取出来
D=inv(D);%%转置
L=tril(A,-1);%%提取矩阵A的下三角
U=triu(A,1);%%提取矩阵A的上三角
B=-D*(L+U);%%雅可比迭代公式
f=D*b;
k=0;
x0=x0;
x=B*x0+f;%%迭代公式
fprintf('k x1_(k) x2_(k) x3_(k)\n');
fprintf('%2d %4.0f %4.0f %4.0f\n',k,x0);
while norm(x-x0)>=eps%%没有到达指定的误差值之前执行循环,不断迭代x0=x;x=B*x0+f;k=k+1;fprintf('%2d %4.0f %4.0f %4.0f\n',k,x0);
endGauss-Seidel迭代法
%%Gauss-seidel迭代法
function x=GaussSeidel(A,b,x0)%%和Jacobi迭代同样的思路,只是公式发生了变化
D=diag(diag(A));
L=tril(A,-1);
C=inv(D+L);
U=triu(A,1);
B=-C*U;
f=C*b;
i=0;
x0=x0;
x=B*x0+f;
fprintf('k x1_(k) x2_(k) x3_(k)\n');
fprintf('%2d %4.0f %4.0f %4.0f\n',k,x0);
for i=1:10x0=x;x=B*x0+f;fprintf('%2d %4.0f %4.0f %4.0f\n',k,x0);
end
二分法
function x = bisectionMethod(A, b, tol)[n, m] = size(A);nb = length(b);if n ~= merror('系数矩阵必须是方的');endif m ~= nberror('b的维数与方程的行数不匹配!');end% 定义二分法的初始下界和上界lower_bound = -1e6;upper_bound = 1e6;% 设置二分法的最大迭代次数max_iterations = 1000;% 循环执行二分法迭代for k = 1:max_iterationslambda = (lower_bound + upper_bound) / 2; % 计算当前迭代的 lambda 值% 解上界对应的方程组并计算残差x_upper = GaussianElimination(A - lambda * eye(n), b);residual_upper = norm(A * x_upper - lambda * x_upper - b);% 解下界对应的方程组并计算残差x_lower = GaussianElimination(A - lower_bound * eye(n), b);residual_lower = norm(A * x_lower - lower_bound * x_lower - b);% 判断是否满足终止条件if abs(residual_upper - residual_lower) < tolbreak;end% 更新下界和上界if residual_upper > residual_lowerupper_bound = lambda;elselower_bound = lambda;endend% 返回最终二分法得到的解x = x_upper;
endfunction x = GaussianElimination(A, b)[n, m] = size(A);nb = length(b);if n ~= merror('系数矩阵必须是方的');endif m ~= nberror('b的维数与方程的行数不匹配!');end% 高斯消元过程for k = 1:n-1% 选主元a_max = abs(A(k, k));r = k;for i = k:nif abs(A(i, k)) > a_maxa_max = abs(A(i, k));r = i;endendif a_max < 1e-15error('系数矩阵奇异,无法匹配方程组');end% 交换两行if r > ktemp = A(k, :);A(k, :) = A(r, :);A(r, :) = temp;temp = b(k);b(k) = b(r);b(r) = temp;end% 消元过程for i = k+1:nm = A(i, k) / A(k, k);for j = k+1:nA(i, j) = A(i, j) - m * A(k, j);endb(i) = b(i) - m * b(k);endend% 回代过程if abs(A(n, n)) < 1e-15error('系数矩阵奇异,无法求解方程组');endx = zeros(size(b));for k = n:-1:1for j = k+1:nb(k) = b(k) - A(k, j) * x(j);endx(k) = b(k) / A(k, k);end
endNewton法
%%Newton法
function x=Newton(fname,dfname,x0,e,N)
%%fname和dfname分别表示f(x)及其导函数的M函数句柄或内嵌函数表达式
if nargin<5,N=500;
end
if nargin<4,e=1e-4;
end
x=x0;
x0=x+2*e;
k=0;
while abs(x0-x)>e&k<N%%大于误差允许值且没有达到迭代次数,继续迭代k=k+1;x0=x;x=x0-feval(fname,x0)/feval(dfname,x0);%%Newton公式fprintf('It.no=%2d x[%2d]=%12.9f\n',k,k,x);
end
if k==N,fprintf('已经达到迭代次数');
endLagrange插值
%%Lagrange插值
function yy=Lagrange(x,y,xi)
m=length(x);%%自变量的长度
n=length(x);%%因变量的长度
if m~=nerror('向量x与y的长度必须一致');
end
s=0;
for i=1:nz=ones(1,length(xi));%%建立一个预备数组for j=1:nif j~=iz=z.*(xi-x(j))/(x(i)-x(j));//%%Lagrange插值公式end
end
s=s+z*y(i);
end
yy=s;相关文章:

数值分析总结
数值分析总结思维导图 Docs 相关代码的使用和注释 列主元Gauss消元法 %%列主元高斯消元法 function xGauss_lzy(A,b)%A为方程组系数矩阵,b为方程组的右侧向量,x为方程组的解 [n,m]size(A);%%得到矩阵A的行和列的宽度 nblength(b);%%方程组右侧向量的长…...

osg demo汇总
1.example_osganimate 演示了路径动画的使用(AnimationPath、AnimationPathCallback),路径动画回调能够做用在Camera、CameraView、MatrixTransform、PositionAttitudeTransform等四种类型的节点上。 演示了osgSim::OverlayNode的使用node 2…...

Leetcode.1590 使数组和能被 P 整除
题目链接 Leetcode.1590 使数组和能被 P 整除 rating : 2039 题目描述 给你一个正整数数组 n u m s nums nums,请你移除 最短 子数组(可以为 空),使得剩余元素的 和 能被 p p p 整除。 不允许 将整个数组都移除。 请你返回你需…...

uniappios请求打开麦克风 uniapp发起请求
第一种 ajax请求方式 uni.request(OBJECT) 参数名类型必填默认值说明平台差异说明urlString是开发者服务器接口地址dataObject/String/ArrayBuffer否请求的参数App(自定义组件编译模式)不支持ArrayBuffer类型headerObject否设置请求的 header,header 中不能设置 Referer。…...
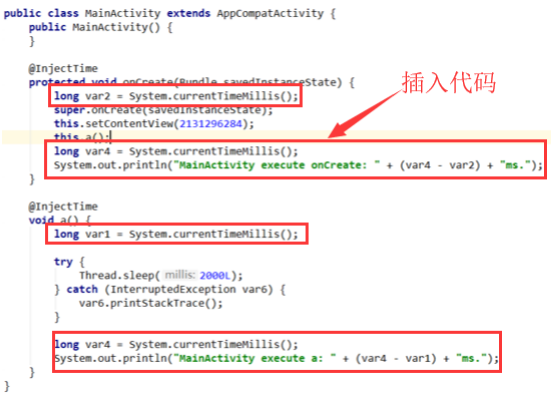
Java 注解在 Android 中的使用场景
Java 元注解有 5 种,常用的是 Target 和 Retention 两个。 其中 Retention 表示保留级别,有三种: RetentionPolicy.SOURCE - 标记的注解仅保留在源码级别中,并被编译器忽略RetentionPolicy.CLASS - 标记的注解在编译时由编译器保…...

【开源】基于Vue和SpringBoot的数字化社区网格管理系统
项目编号: S 042 ,文末获取源码。 \color{red}{项目编号:S042,文末获取源码。} 项目编号:S042,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块三、开发背景四、系统展示五、核心源码5…...

Go语言简要介绍
Golang是一种编程语言,也称为Go或者Go语言。它是由Google开发的一种编译型、静态类型的语言。Golang的目标是提高程序开发的效率,同时保证程序的性能和安全。 Golang在语法结构上类似于C语言,但是通过引入新的概念和语法,比如gor…...

STM32H7 RTC及PC13问题
程序加了RTC时间过后,发现原本的RTC定时唤醒中断也不好使了,开始以为是PC13入侵检测引脚问题,经过测试,发现了一个大问题,当使用 HAL_RTC_SetTime(&hrtc, &time, RTC_FORMAT_BCD); 函数后,RTC变得…...
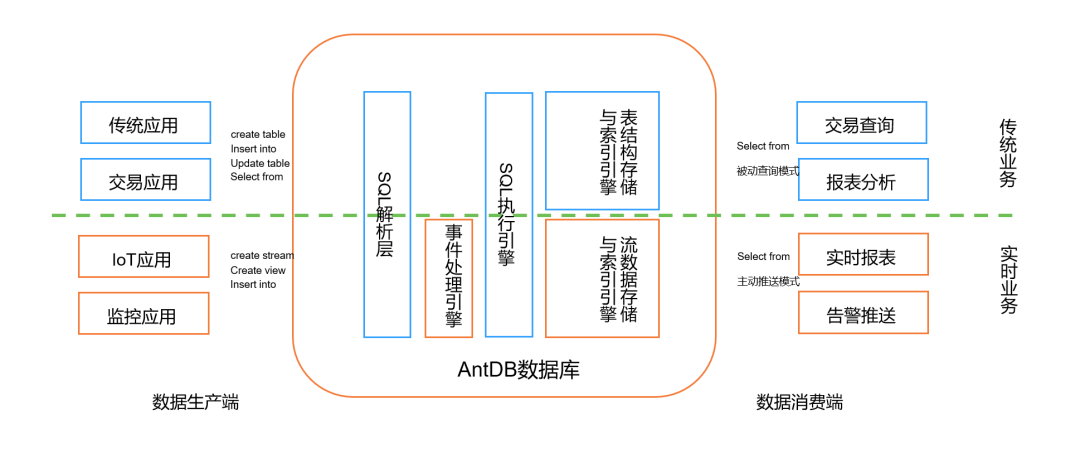
AntDB“超融合+流式实时数仓”——颠覆50年未变的数据库内核
流式处理引擎,颠覆50年未变的数据库内核 流式处理的概念 2001年9月11日,美国世贸大楼被袭击,美国国防部第一次将“主动预警”纳入国防的宏观战略规划。而IBM作为当时全球最大的IT公司,承担了大量基础支撑软件研发的任务。其中200…...
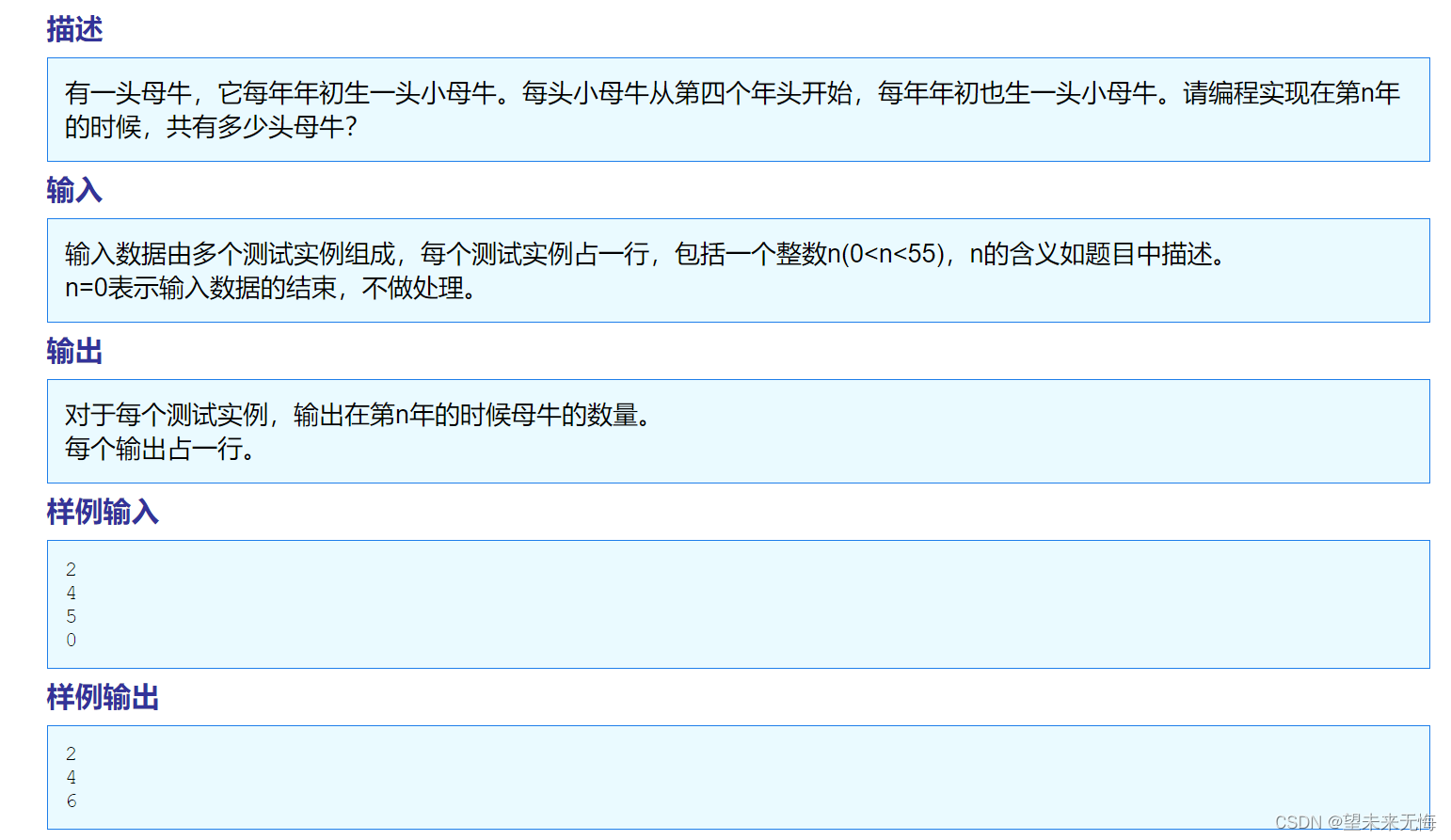
TZOJ 1376 母牛的故事(递推和递归)
答案1(递推): #include<stdio.h> int main() {int n0,i0;int a[55] { 0,1,2,3,4 }; //数组下标就相当于过了几年,以第四年母牛生出的第一只小母牛成年为周期,初始化前四年的值while (scanf("%d", …...
五种多目标优化算法(MOPSO、MOAHA、NSGA2、NSGA3、MOGWO)求解微电网多目标优化调度(MATLAB)
一、多目标优化算法简介 (1)多目标粒子群优化算法MOPSO 多目标应用:基于多目标粒子群优化算法MOPSO求解微电网多目标优化调度(MATLAB代码)-CSDN博客 (2)多目标人工蜂鸟算法(MOAHA…...
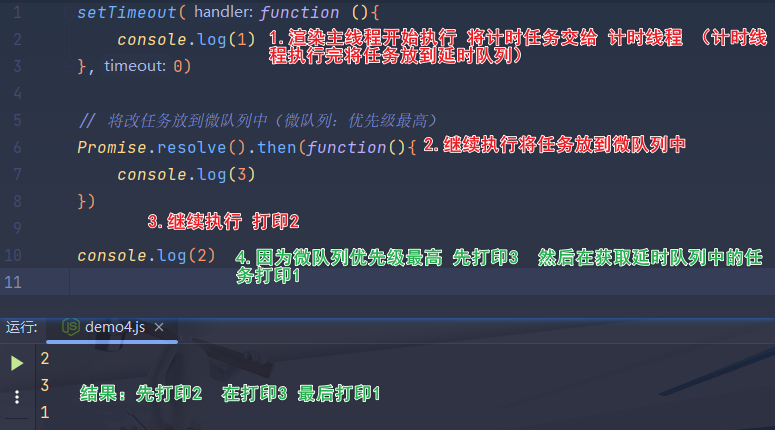
01_原理-事件循环
01_原理-事件循环 文章目录 01_原理-事件循环一、浏览器的进程模型①:何为进程?②:何为线程?③:浏览器有哪些进程和线程? 二、渲染主线程是如何工作的?三、若干解释①:何为异步&…...

Redis的性能,哨兵模式,集群,
Redis的性能管理; redis的数据保存在内存中 redis-cli info memory redis内存使用info memory命令参数解析 used_memory:236026888 由 Redis 分配器分配的内存总量,包含了redis进程内部的开销和数据占用的内存,以字节(byte)…...
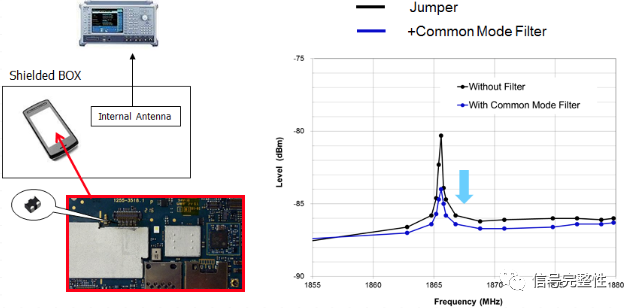
如何选择共模噪声滤波器
在当前电子产品中,绝大多数的高速信号都使用地差分对结构。 差分结构有一个好处就是可以降低外界对信号的干扰,但是由于设计的原因,在传输结构上还会受到共模噪声的影响。 共模噪声滤波器就可以用于抑制不必要的共模噪声,而不会对…...

Python与设计模式--模板模式
23种计模式之 前言 (5)单例模式、工厂模式、简单工厂模式、抽象工厂模式、建造者模式、原型模式、(7)代理模式、装饰器模式、适配器模式、门面模式、组合模式、享元模式、桥梁模式、(11)策略模式、责任链模式、命令模式、中介者模…...
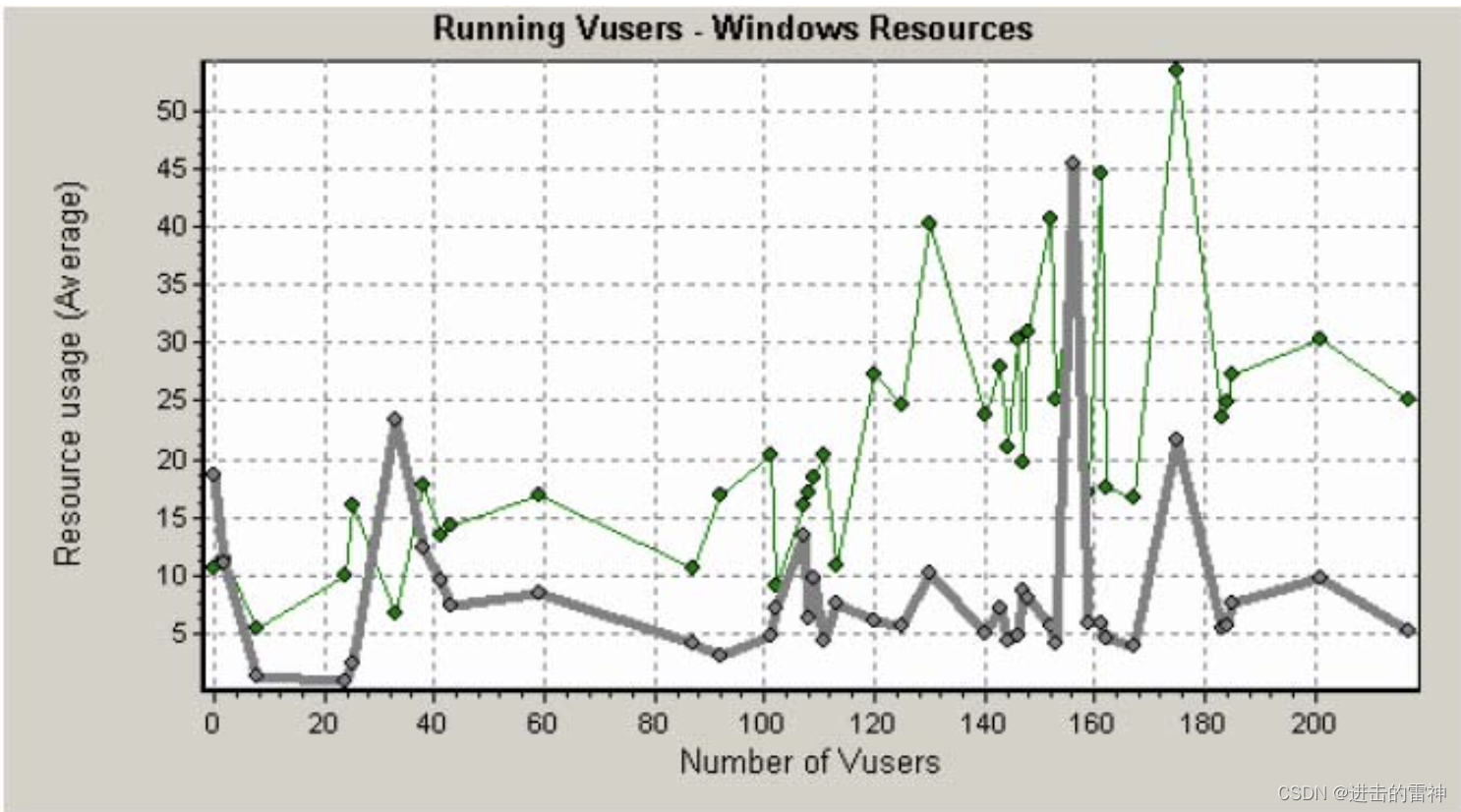
LoadRunner自动化测试工具的应用
目录 第一部分:Loadrunner的简介 1.1 安装注意事项 1.2 协议的选择或者 VUSER 类型的选取 1.3 LR 的基本原理 1.4 测试脚本录制/分配所遵循的几个原则 第二部分:录制脚本 2.1 录制脚本前需要理解的几个基本概念 2.1.1 事务(Transaction) 2.1.2 集合点(Rendezvous) 2.1…...

工厂模式是一种创建对象的设计模式,使用工厂类来创建对象,而不是直接使用 new 关键字来创建对象。
文章目录 示例代码virtual std::string Operation() const = 0;如何理解std::string Operation() const override {这句如何理解?Factory 类包含一个静态方法 CreateProduct,它根据传入的类型参数来创建并返回具体的产品实例。这句话理解?std::unique_ptr<Product> pr…...

NET MVC中使用Element-Plus框架编写组件
一、目的 在NET MVC中使用Element-Plus编写可重复使用的组件。 二、准备工作 2.1 NET MVC项目 2.2 MVC项目中使用Element-Plus框架。不熟悉的可以参考此文章: NET MVC中如何使用Element-Plus-CSDN博客 三、组件编写 3.1、新建一个MVC的部分视图页面ÿ…...

在线文库系统 转码功能源代码展示 支持文档在线预览查阅功能
1、支持 pdf,doc,docx,ppt,pptx,txt,xlsx,xls,csv,zip,epub,ai,psd 格式的文件 2、文库系统的上传界面,用户可以进行上传自己的文件,然后自定义文档售价,来赚取金额。 3、文库系统的部分代码披露: <template><div clas…...

Linux /etc/shadow密码生成操作示例
一. 前言 之前学习过Linux文件系统下/etc/shadow里面保存着各个用户名的密码,并且密码是通过MD5算法加盐的方式生成的。但是一直没有自己真正动手生成过,今天,就来自己动手写代码生成下。 二. 代码验证/etc/shadow中密码 1. 通过passwd命令生…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
