Leetcode.1590 使数组和能被 P 整除
题目链接
Leetcode.1590 使数组和能被 P 整除
rating : 2039
题目描述
给你一个正整数数组 n u m s nums nums,请你移除 最短 子数组(可以为 空),使得剩余元素的 和 能被 p p p 整除。 不允许 将整个数组都移除。
请你返回你需要移除的最短子数组的长度,如果无法满足题目要求,返回 − 1 -1 −1 。
子数组 定义为原数组中连续的一组元素。
示例 1:
输入:nums = [3,1,4,2], p = 6
输出:1
解释:nums 中元素和为 10,不能被 p 整除。我们可以移除子数组 [4] ,剩余元素的和为 6 。
示例 2:
输入:nums = [6,3,5,2], p = 9
输出:2
解释:我们无法移除任何一个元素使得和被 9 整除,最优方案是移除子数组 [5,2] ,剩余元素为 [6,3],和为 9 。
提示3:
输入:nums = [1,2,3], p = 3
输出:0
解释:和恰好为 6 ,已经能被 3 整除了。所以我们不需要移除任何元素。
提示4:
输入:nums = [1,2,3], p = 7
输出:-1
解释:没有任何方案使得移除子数组后剩余元素的和被 7 整除。
提示5:
输入:nums = [1000000000,1000000000,1000000000], p = 3
输出:0
提示:
- 1 ≤ n u m s . l e n g t h ≤ 1 0 5 1 \leq nums.length \leq 10^5 1≤nums.length≤105
- 1 ≤ n u m s [ i ] ≤ 1 0 9 1 \leq nums[i] \leq 10^9 1≤nums[i]≤109
- 1 ≤ p ≤ 1 0 9 1 \leq p \leq 10^9 1≤p≤109
解法:前缀和 + 哈希表
假设整个数组 n u m s nums nums 的和为 s s s,那么 k = s m o d p k = s\ mod\ p k=s mod p。
- 如果 k = 0 k = 0 k=0,说明整个数组的和都可以被 p p p 整除,所以不需要移除元素,直接返回 0 0 0;
- 如果 k ≠ 0 k \neq 0 k=0,假设我们需要移除的这个子数组和为 t t t,那么 t m o d p = k t\ mod\ p = k t mod p=k,并且还要要求这个子数组的长度是最短的。
假设区间 [ j , i ] [j,i] [j,i] 的子数组满足这个条件,我们用 s u m sum sum 表示 n u m s nums nums 的前缀和,即:
( s u m [ i ] − s u m [ j − 1 ] ) m o d p = k (sum[i] - sum[j-1])\ mod\ p = k (sum[i]−sum[j−1]) mod p=k
再转换一下:
s u m [ j − 1 ] m o d p = s u m [ i ] m o d p − k sum[j-1]\ mod\ p = sum[i]\ mod\ p - k sum[j−1] mod p=sum[i] mod p−k
由于 s u m [ j ] m o d p − k sum[j]\ mod\ p - k sum[j] mod p−k 有可能是负数,所以我们需要再将其转换为整数:
s u m [ j − 1 ] m o d p = ( s u m [ i ] m o d p − k + p ) m o d p sum[j-1]\ mod\ p = (sum[i]\ mod\ p - k + p)\ mod\ p sum[j−1] mod p=(sum[i] mod p−k+p) mod p
我们用哈希表来记录这个 s u m [ i ] m o d p sum[i]\ mod\ p sum[i] mod p,值就是其对应的下标 i i i。
我们令 k e y = ( s u m [ i ] m o d p − k + p ) m o d p key = (sum[i]\ mod\ p - k + p)\ mod\ p key=(sum[i] mod p−k+p) mod p,如果对于当前 k e y key key,哈希表 m p mp mp 中有记录,则 j = m p [ k e y ] j = mp[key] j=mp[key]。说明移除此时的子数组 [ j , i ] [j,i] [j,i] 就能使 n u m s nums nums 的剩余元素满足条件,那么我们更新答案 a n s ans ans。
注意:
- 哈希表 m p mp mp 初始时需要加入 { 0 , − 1 } \{0 , -1 \} {0,−1};
- a n s ans ans 是最终的答案,需要移除的最短子数组的长度,初始化为一个较大的数即可;
时间复杂度: O ( n ) O(n) O(n)
C++代码:
using LL = long long;class Solution {
public:int minSubarray(vector<int>& nums, int p) {int n = nums.size();LL sum = 0;for(auto x:nums) sum += x;int k = sum % p;if(k == 0) return 0;unordered_map<int,int> mp{{0 , -1}};int ans = n;sum = 0;for(int i = 0;i < n;i++){sum += nums[i];auto key = (sum % p - k + p)%p;if(mp.find(key) != mp.end()){auto j = mp[key];ans = min(ans , i - j);}mp[sum % p] = i;}return ans == n ? -1 : ans;}
};
相关文章:

Leetcode.1590 使数组和能被 P 整除
题目链接 Leetcode.1590 使数组和能被 P 整除 rating : 2039 题目描述 给你一个正整数数组 n u m s nums nums,请你移除 最短 子数组(可以为 空),使得剩余元素的 和 能被 p p p 整除。 不允许 将整个数组都移除。 请你返回你需…...

uniappios请求打开麦克风 uniapp发起请求
第一种 ajax请求方式 uni.request(OBJECT) 参数名类型必填默认值说明平台差异说明urlString是开发者服务器接口地址dataObject/String/ArrayBuffer否请求的参数App(自定义组件编译模式)不支持ArrayBuffer类型headerObject否设置请求的 header,header 中不能设置 Referer。…...
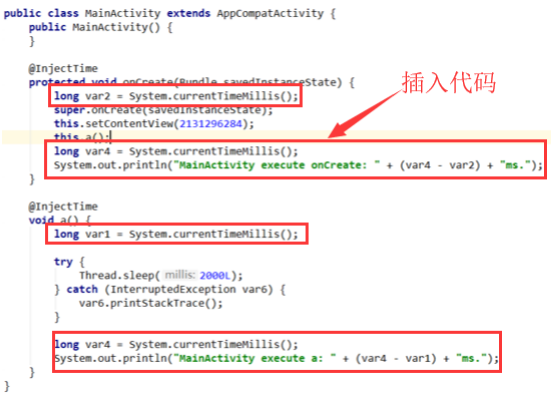
Java 注解在 Android 中的使用场景
Java 元注解有 5 种,常用的是 Target 和 Retention 两个。 其中 Retention 表示保留级别,有三种: RetentionPolicy.SOURCE - 标记的注解仅保留在源码级别中,并被编译器忽略RetentionPolicy.CLASS - 标记的注解在编译时由编译器保…...

【开源】基于Vue和SpringBoot的数字化社区网格管理系统
项目编号: S 042 ,文末获取源码。 \color{red}{项目编号:S042,文末获取源码。} 项目编号:S042,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块三、开发背景四、系统展示五、核心源码5…...

Go语言简要介绍
Golang是一种编程语言,也称为Go或者Go语言。它是由Google开发的一种编译型、静态类型的语言。Golang的目标是提高程序开发的效率,同时保证程序的性能和安全。 Golang在语法结构上类似于C语言,但是通过引入新的概念和语法,比如gor…...

STM32H7 RTC及PC13问题
程序加了RTC时间过后,发现原本的RTC定时唤醒中断也不好使了,开始以为是PC13入侵检测引脚问题,经过测试,发现了一个大问题,当使用 HAL_RTC_SetTime(&hrtc, &time, RTC_FORMAT_BCD); 函数后,RTC变得…...
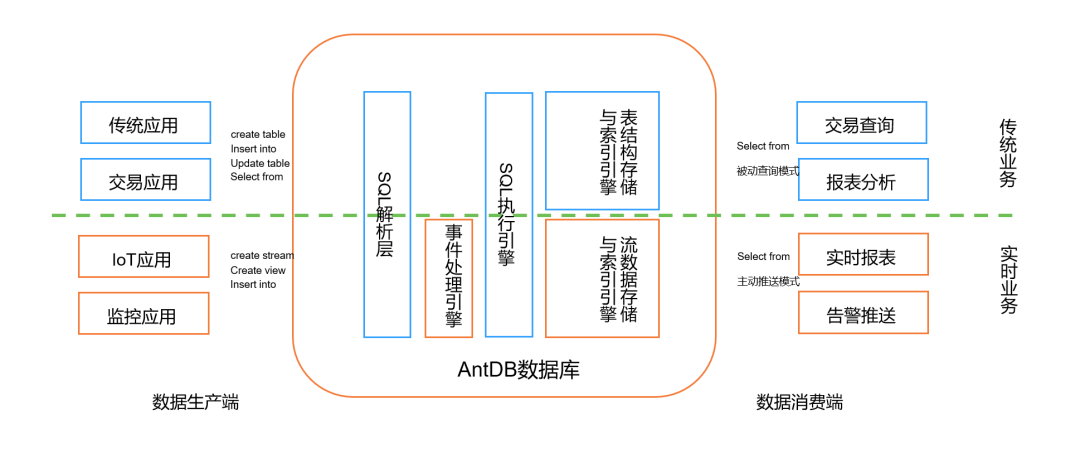
AntDB“超融合+流式实时数仓”——颠覆50年未变的数据库内核
流式处理引擎,颠覆50年未变的数据库内核 流式处理的概念 2001年9月11日,美国世贸大楼被袭击,美国国防部第一次将“主动预警”纳入国防的宏观战略规划。而IBM作为当时全球最大的IT公司,承担了大量基础支撑软件研发的任务。其中200…...
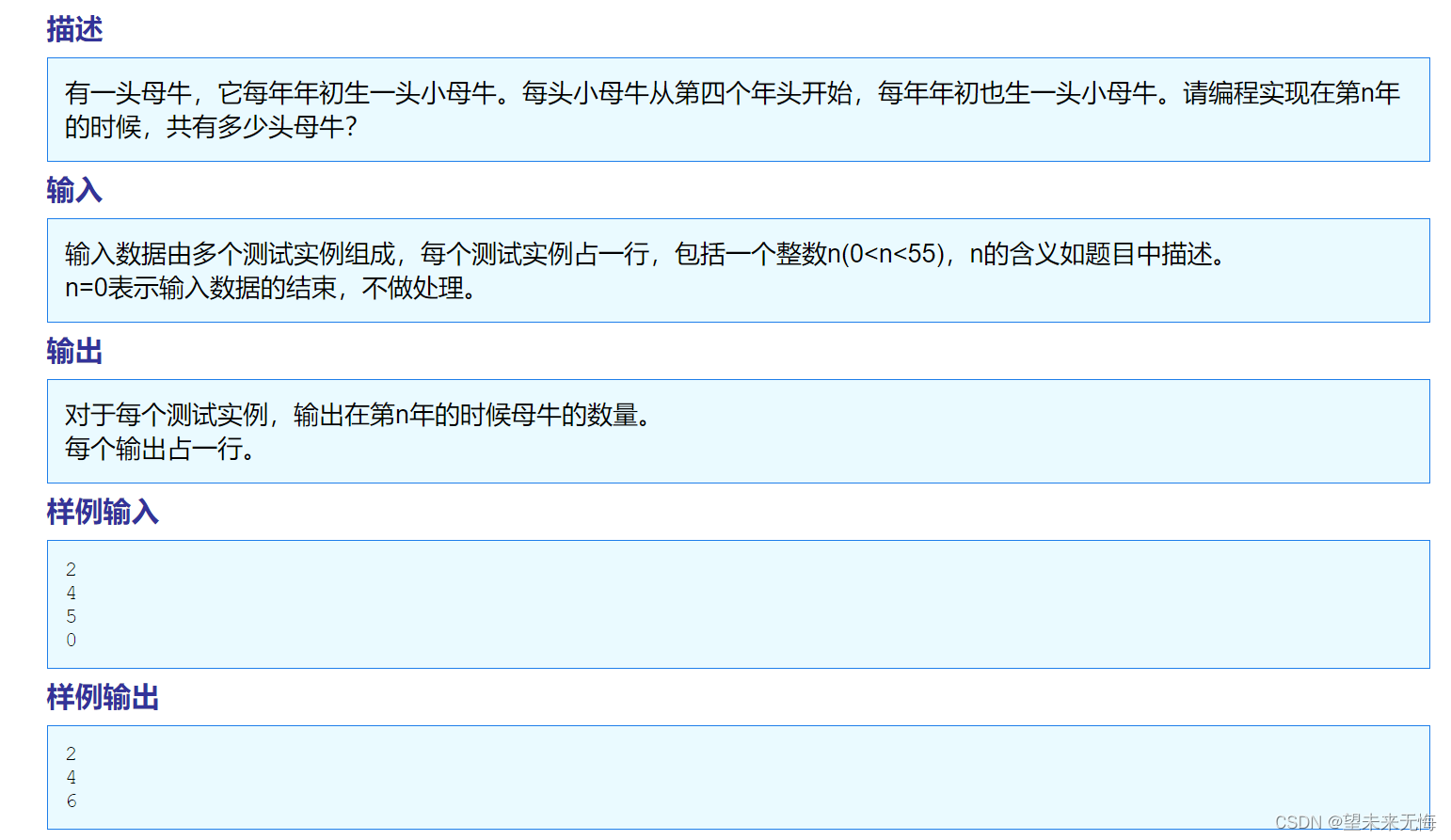
TZOJ 1376 母牛的故事(递推和递归)
答案1(递推): #include<stdio.h> int main() {int n0,i0;int a[55] { 0,1,2,3,4 }; //数组下标就相当于过了几年,以第四年母牛生出的第一只小母牛成年为周期,初始化前四年的值while (scanf("%d", …...
五种多目标优化算法(MOPSO、MOAHA、NSGA2、NSGA3、MOGWO)求解微电网多目标优化调度(MATLAB)
一、多目标优化算法简介 (1)多目标粒子群优化算法MOPSO 多目标应用:基于多目标粒子群优化算法MOPSO求解微电网多目标优化调度(MATLAB代码)-CSDN博客 (2)多目标人工蜂鸟算法(MOAHA…...
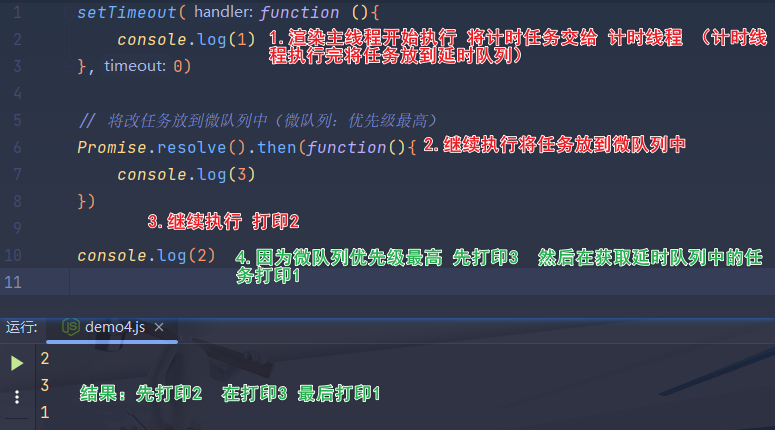
01_原理-事件循环
01_原理-事件循环 文章目录 01_原理-事件循环一、浏览器的进程模型①:何为进程?②:何为线程?③:浏览器有哪些进程和线程? 二、渲染主线程是如何工作的?三、若干解释①:何为异步&…...

Redis的性能,哨兵模式,集群,
Redis的性能管理; redis的数据保存在内存中 redis-cli info memory redis内存使用info memory命令参数解析 used_memory:236026888 由 Redis 分配器分配的内存总量,包含了redis进程内部的开销和数据占用的内存,以字节(byte)…...
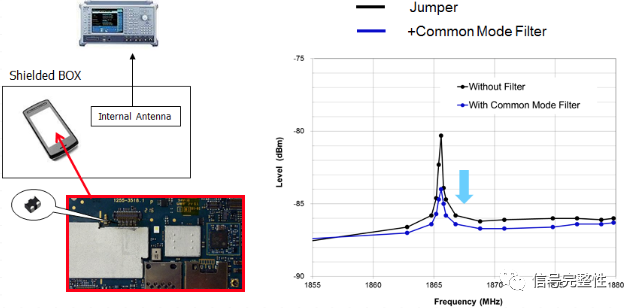
如何选择共模噪声滤波器
在当前电子产品中,绝大多数的高速信号都使用地差分对结构。 差分结构有一个好处就是可以降低外界对信号的干扰,但是由于设计的原因,在传输结构上还会受到共模噪声的影响。 共模噪声滤波器就可以用于抑制不必要的共模噪声,而不会对…...

Python与设计模式--模板模式
23种计模式之 前言 (5)单例模式、工厂模式、简单工厂模式、抽象工厂模式、建造者模式、原型模式、(7)代理模式、装饰器模式、适配器模式、门面模式、组合模式、享元模式、桥梁模式、(11)策略模式、责任链模式、命令模式、中介者模…...
LoadRunner自动化测试工具的应用
目录 第一部分:Loadrunner的简介 1.1 安装注意事项 1.2 协议的选择或者 VUSER 类型的选取 1.3 LR 的基本原理 1.4 测试脚本录制/分配所遵循的几个原则 第二部分:录制脚本 2.1 录制脚本前需要理解的几个基本概念 2.1.1 事务(Transaction) 2.1.2 集合点(Rendezvous) 2.1…...

工厂模式是一种创建对象的设计模式,使用工厂类来创建对象,而不是直接使用 new 关键字来创建对象。
文章目录 示例代码virtual std::string Operation() const = 0;如何理解std::string Operation() const override {这句如何理解?Factory 类包含一个静态方法 CreateProduct,它根据传入的类型参数来创建并返回具体的产品实例。这句话理解?std::unique_ptr<Product> pr…...

NET MVC中使用Element-Plus框架编写组件
一、目的 在NET MVC中使用Element-Plus编写可重复使用的组件。 二、准备工作 2.1 NET MVC项目 2.2 MVC项目中使用Element-Plus框架。不熟悉的可以参考此文章: NET MVC中如何使用Element-Plus-CSDN博客 三、组件编写 3.1、新建一个MVC的部分视图页面ÿ…...

在线文库系统 转码功能源代码展示 支持文档在线预览查阅功能
1、支持 pdf,doc,docx,ppt,pptx,txt,xlsx,xls,csv,zip,epub,ai,psd 格式的文件 2、文库系统的上传界面,用户可以进行上传自己的文件,然后自定义文档售价,来赚取金额。 3、文库系统的部分代码披露: <template><div clas…...

Linux /etc/shadow密码生成操作示例
一. 前言 之前学习过Linux文件系统下/etc/shadow里面保存着各个用户名的密码,并且密码是通过MD5算法加盐的方式生成的。但是一直没有自己真正动手生成过,今天,就来自己动手写代码生成下。 二. 代码验证/etc/shadow中密码 1. 通过passwd命令生…...
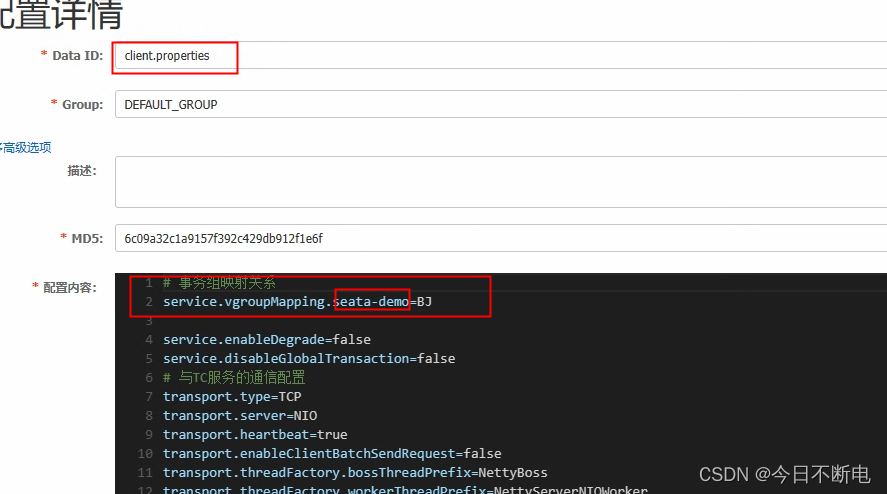
seata集成springboot的一些错误小计
1 seata依赖没找到 dependencies.dependency.version for com.alibaba.cloud:spring-cloud-starter-alibaba-seata:jar is missing. line 126, column 21错误原因:未指定具体的seata版本 解决 <!-- https://mvnrepository.com/artifact/com.alibaba.cloud/spring-cloud-st…...
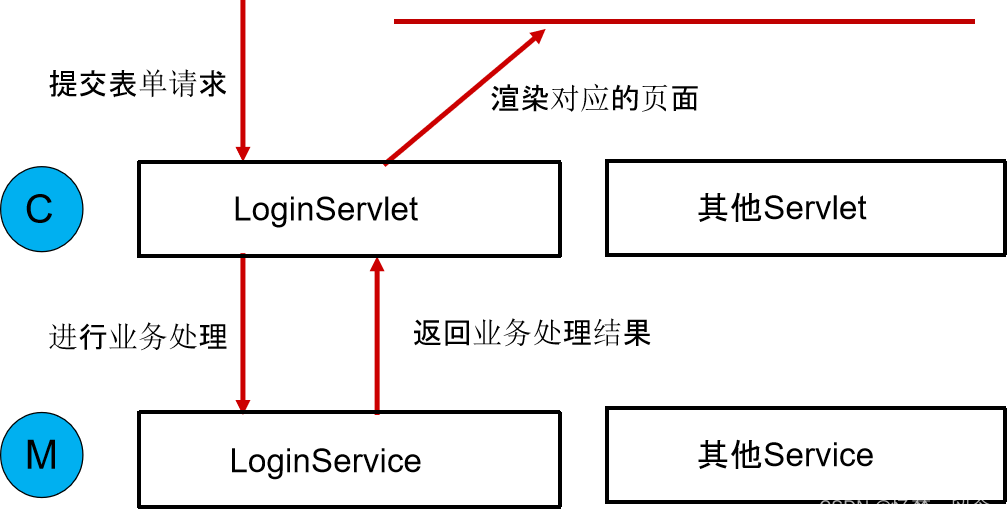
springmvc(基础学习整合)
SpringMVC是Spring框架提供的构建Web应用程序的全功能MVC模块。 在SpringMVC的各个组件中,处理器映射器、处理器适配器、视图解析器称为SpringMVC的三大组件。 springMVC基本介绍: http://t.csdnimg.cn/TOzw9 MVC是一种设计思想,将一个应…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...

PostgreSQL 与 SQL 基础:为 Fast API 打下数据基础
在构建任何动态、数据驱动的Web API时,一个稳定高效的数据存储方案是不可或缺的。对于使用Python FastAPI的开发者来说,深入理解关系型数据库的工作原理、掌握SQL这门与数据库“对话”的语言,以及学会如何在Python中操作数据库,是…...

vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能
vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能 查看官网:https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...

CentOS 7.9安装Nginx1.24.0时报 checking for LuaJIT 2.x ... not found
Nginx1.24编译时,报LuaJIT2.x错误, configuring additional modules adding module in /www/server/nginx/src/ngx_devel_kit ngx_devel_kit was configured adding module in /www/server/nginx/src/lua_nginx_module checking for LuaJIT 2.x ... not…...
