scipy 笔记:scipy.spatial.distance
1 pdist
计算n维空间中观测点之间的成对距离。
scipy.spatial.distance.pdist(X, metric='euclidean', *, out=None, **kwargs)1.1 主要参数
| X | 一个m行n列的数组,表示n维空间中的m个原始观测点 |
| metric | 使用的距离度量 |
| out | 输出数组。如果非空,压缩的距离矩阵Y将存储在此数组中 |
1.2 举例
import numpy as np
from scipy.spatial.distance import pdistx = np.array([[2, 0, 2], [2, 2, 3], [-2, 4, 5], [0, 1, 9], [2, 2, 4]])
#5个元素,每个元素3维pdist(x)
#array([2.23606798, 6.40312424, 7.34846923, 2.82842712, 4.89897949,6.40312424, 1. , 5.38516481, 4.58257569, 5.47722558])
'''
10个元素,分别表示:第1个点和第2个点之间的距离
第1个点和第3个点之间的距离
第1个点和第4个点之间的距离
第1个点和第5个点之间的距离
第2个点和第3个点之间的距离
第2个点和第4个点之间的距离
第2个点和第5个点之间的距离
第3个点和第4个点之间的距离
第3个点和第5个点之间的距离
第4个点和第5个点之间的距离
'''2 cdist
计算两个输入集合中每对元素之间的距离
scipy.spatial.distance.cdist(XA, XB, metric='euclidean', *, out=None, **kwargs)2.1 主要参数
| XA | mA*n的矩阵,表示mA个元素,每个元素n维特征 |
| XB | mBn的矩阵,表示mB个元素,每个元素n维特征 |
| metric | 使用的距离度量 |
| out | 输出数组(mA*mB)。如果非空,压缩的距离矩阵Y将存储在此数组中 |
2.2 举例
import numpy as np
from scipy.spatial.distance import cdistx = np.array([[2, 0, 2], [2, 2, 3], [-2, 4, 5], [0, 1, 9], [2, 2, 4]])cdist(x,x)
'''
array([[0. , 2.23606798, 6.40312424, 7.34846923, 2.82842712],[2.23606798, 0. , 4.89897949, 6.40312424, 1. ],[6.40312424, 4.89897949, 0. , 5.38516481, 4.58257569],[7.34846923, 6.40312424, 5.38516481, 0. , 5.47722558],[2.82842712, 1. , 4.58257569, 5.47722558, 0. ]])
'''y=[[1,2,3]]
cdist(x,y)
'''
array([[2.44948974],[1. ],[4.12310563],[6.164414 ],[1.41421356]])
'''cdist(y,x)
'''
array([[2.44948974, 1. , 4.12310563, 6.164414 , 1.41421356]])
'''3 squareform
将距离向量的向量形式转换为方阵形式的距离矩阵,反之亦然。
scipy.spatial.distance.squareform(X, force='no', checks=True)
3.1 举例
import numpy as np
from scipy.spatial.distance import *x = np.array([[2, 0, 2], [2, 2, 3], [-2, 4, 5], [0, 1, 9], [2, 2, 4]])dist_vec=pdist(x)
dist_vec
'''
array([2.23606798, 6.40312424, 7.34846923, 2.82842712, 4.89897949,6.40312424, 1. , 5.38516481, 4.58257569, 5.47722558])
'''dist_mat=squareform(dist_vec)
dist_mat
'''
array([[0. , 2.23606798, 6.40312424, 7.34846923, 2.82842712],[2.23606798, 0. , 4.89897949, 6.40312424, 1. ],[6.40312424, 4.89897949, 0. , 5.38516481, 4.58257569],[7.34846923, 6.40312424, 5.38516481, 0. , 5.47722558],[2.82842712, 1. , 4.58257569, 5.47722558, 0. ]])
'''squareform(dist_mat)
'''
array([2.23606798, 6.40312424, 7.34846923, 2.82842712, 4.89897949,6.40312424, 1. , 5.38516481, 4.58257569, 5.47722558])
'''4 directed_hausdorff
- 计算两个二维数组之间的定向豪斯多夫距离
- 通常用于衡量两个点集合的相似性
scipy.spatial.distance.directed_hausdorff(u, v, seed=0)数学笔记/scipy 笔记:豪斯多夫距离(Hausdorff )_python 豪斯多夫距离-CSDN博客
4.1 主要参数
| u | (M,N)大小的数组 M 表示点的数量,N 表示每个点的维度 |
| v | (O,N)大小的数组 O 表示点的数量,N 表示每个点的维度 |
4.2 返回内容
| d | u 和 v 之间的定向豪斯多夫距离 |
| index_1 | 在数组u中贡献豪斯多夫对的点的索引 |
| index_2 | 在数组v中贡献豪斯多夫对的点的索引 |
4.3 举例
import numpy as np
from scipy.spatial.distance import *u = np.array([(1.0, 0.0),(0.0, 1.0),(-1.0, 0.0),(0.0, -1.0)])
v = np.array([(2.0, 0.0),(0.0, 2.0),(-2.0, 0.0),(0.0, -4.0)])directed_hausdorff(u,v)
#(2.23606797749979, 3, 0)5 is_valid_dm
判断输入数组是否为有效的距离矩阵
scipy.spatial.distance.is_valid_dm(D, tol=0.0, throw=False, name='D', warning=False)5.1 主要参数
| D | 用于测试有效性的候选对象 |
| tol | 距离矩阵应该是对称的。tol是条目ij和ji之间的最大差异,以便将距离度量视为对称 |
5.2 举例
import numpy as np
from scipy.spatial.distance import *d = np.array([[0.0, 1.1, 1.2, 1.3],[1.1, 0.0, 1.0, 1.4],[1.2, 1.0, 0.0, 1.5],[1.3, 1.4, 1.5, 0.0]])
is_valid_dm(d)
#Trueis_valid_dm([[0, 2, 2], [2, 0, 2]])
#形状不对is_valid_dm([[0, 1, 1], [1, 2, 3], [1, 3, 0]])
#对角线不为0is_valid_dm([[0, 1, 3], [2, 0, 1], [3, 1, 0]])
#不对称6 is_valid_y
scipy.spatial.distance.is_valid_y(y, warning=False, throw=False, name=None)判断输入数组是否为有效的压缩距离矩阵。
压缩距离矩阵必须是1维的numpy数组。它们的长度必须是一些正整数n的二项系数
6.1 主要参数
| y | 压缩距离矩阵 |
6.2 举例
import numpy as np
from scipy.spatial.distance import *is_valid_y([1.0, 1.2, 1.0, 0.5, 1.3, 0.9])
#True
#长度为6,合理长度,所以返回Trueis_valid_y([1.0, 1.2, 1.0, 0.5, 1.3, 0.9,1.5])
#False
#长度为7,不合理长度,所以返回False7 两个数字向量之间的距离
7.1 braycurtis
计算两个一维数组之间的布雷-柯蒂斯距离
scipy.spatial.distance.braycurtis(u, v, w=None)

7.1.1 主要参数
| u | (N,) 输入数组 |
| v | (N,) 输入数组 |
| w | (N,) u和v中每个值的权重 |
7.1.2 举例
基本上后面都是一样的,就不举例了
import numpy as np
from scipy.spatial.distance import *braycurtis([1,1,0],[0,1,0])#0.3333333333333333
7.2 canberra
scipy.spatial.distance.canberra(u, v, w=None)
7.3 chebyshev
scipy.spatial.distance.chebyshev(u, v, w=None)

7.4 cityblock
曼哈顿距离
scipy.spatial.distance.cityblock(u, v, w=None)
7.5 correlation
scipy.spatial.distance.correlation(u, v, w=None, centered=True)
7.6 cosine
scipy.spatial.distance.cosine(u, v, w=None)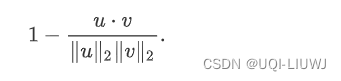
7.7 euclidean
scipy.spatial.distance.euclidean(u, v, w=None)7.8 jensenshannon
scipy.spatial.distance.jensenshannon(p, q, base=None, *, axis=0, keepdims=False)两个概率向量p,q之间的JS距离
如果p和q的总和不为1.0,该程序将对其进行归一化


7.8.1 主要参数
| p | 左侧概率向量 |
| q | 右侧概率向量 |
| base | 用于计算输出的对数底数 |
| axis | 沿着哪个轴计算JS距离 |
7.8.2 举例
import numpy as np
from scipy.spatial.distance import *jensenshannon([1.0, 0.0, 0.0], [0.0, 1.0, 0.0])
#0.8325546111576977jensenshannon([1.0, 0.0, 0.0], [0.0, 1.0, 0.0],2)
#1.0a = np.array([[1, 2, 3, 4],[5, 6, 7, 8],[9, 10, 11, 12]])
b = np.array([[13, 14, 15, 16],[17, 18, 19, 20],[21, 22, 23, 24]])
jensenshannon(a, b, axis=0)
#array([0.19542878, 0.14476971, 0.11383771, 0.09276358])jensenshannon(a, b, axis=1)
#array([0.14023394, 0.03991063, 0.02018153])7.9 mahalanobis
马氏距离
scipy.spatial.distance.mahalanobis(u, v, VI)

7.9.1 主要参数
| u | 输入向量 |
| v | 输入向量 |
| VI | 协方差矩阵的逆,也即上面公式中的 |
7.9.2 举例
import numpy as np
from scipy.spatial.distance import *iv = [[1, 0.5, 0.5], [0.5, 1, 0.5], [0.5, 0.5, 1]]mahalanobis([1, 0, 0], [0, 1, 0], iv)
#1.07.10 minkowski
闵可夫斯基距离
scipy.spatial.distance.minkowski(u, v, p=2, w=None)
7.11 seuclidean
标准欧氏距离
scipy.spatial.distance.seuclidean(u, v, V)

V[i]是针对点集中所有第i个分量计算得到的方差
7.12 sqeuclidean
平方欧氏距离
scipy.spatial.distance.sqeuclidean(u, v, w=None)
8 两个布尔向量距离
8.1 dice
scipy.spatial.distance.dice(u, v, w=None)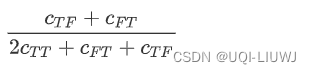
CTF表示u是T,v是F,其他类似
8.2 hamming
scipy.spatial.distance.hamming(u, v, w=None)
8.3 jaccard
scipy.spatial.distance.jaccard(u, v, w=None)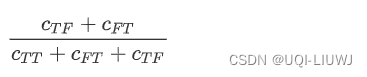
8.4 kulczynski1
scipy.spatial.distance.kulczynski1(u, v, *, w=None)
8.5 rogerstanimoto
scipy.spatial.distance.rogerstanimoto(u, v, w=None)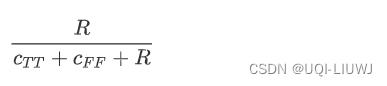

8.6 russellrao

8.7 sokalmichener
scipy.spatial.distance.sokalmichener(u, v, w=None)
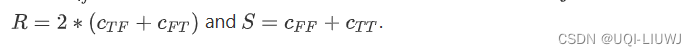
8.8 sokalsneath
scipy.spatial.distance.sokalsneath(u, v, w=None)

8.9 yule
scipy.spatial.distance.yule(u, v, w=None)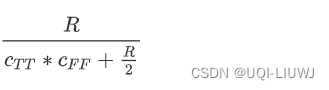

相关文章:

scipy 笔记:scipy.spatial.distance
1 pdist 计算n维空间中观测点之间的成对距离。 scipy.spatial.distance.pdist(X, metriceuclidean, *, outNone, **kwargs) 1.1 主要参数 X一个m行n列的数组,表示n维空间中的m个原始观测点metric使用的距离度量out输出数组。如果非空,压缩的距离矩阵…...

java video audio encoder
引言 在现代互联网的时代,视频和音频已经成为人们生活中不可或缺的一部分。而在计算机科学中,视频和音频编码器则是将原始的视频和音频数据转换为可压缩格式的关键技术。在本文中,我们将探讨基于Java的视频和音频编码器的使用。 什么是视频…...

TypeScript 中声明类型的方法
1、使用:运算符来为变量和函数参数指定类型。例如: let num: number 5; function add(a: number, b: number): number {return a b; }2、使用 type 关键字来声明自定义类型别名。例如: type Point {x: number;y: number; };3、使用 interface 关键字…...
显示器校准软件BetterDisplay Pro mac中文版介绍
BetterDisplay Pro mac是一款显示器校准软件,可以帮助用户调整显示器的颜色和亮度,以获得更加真实、清晰和舒适的视觉体验。 BetterDisplay Pro mac软件特点 - 显示器校准:可以根据不同的需求和环境条件调整显示器的颜色、亮度和对比度等参数…...

Element UI 走马灯 实现鼠标滚动切换页面
鼠标滚动切换页面 elementui Carousel 走马灯鼠标滚轮事件实现 一、在轮播图外的盒子外添加鼠标滚轮事件,触发GoWheel函数。 wheel"goWheel"二、通过判断deltaY的数值来触发相应事件 它检查滚轮事件的deltaY属性是否大于0 event.deltaY当鼠标滚轮向下…...

在Docker上部署Springboot项目
在Docker上部署Springboot项目 ###1.安装docker 2.安装mysql 拉 Mysql 镜像 docker pull mysql:5.7.31运行 Mysql 5.7.31 第一次运行需要设置密码 docker run -d --name myMysql -p 9506:3306 -v /data/mysql:/var/lib/mysql -e MYSQL_ROOT_PASSWORD1234 mysql:5.7.31不是…...

2024中国眼博会,全国眼康与眼镜品牌加盟展会,北京眼健康展
立足北京,面向全球,2024第六届CEYEE中国眼博会,将以大规模的展览面积在4月与您相会; ——春天是万物复苏的季节,更是企业开拓市场,抓住春季发展机遇的重要时节;第六届CEYEE中国眼博会将在2024年…...

C++学习 --谓词
目录 1, 什么是谓词 1-1, 一元谓词 1-2, 二元谓词 1, 什么是谓词 返回bool类型的仿函数, 叫着谓词, 分为一元谓词和二元谓词 1-1, 一元谓词 operator()接收一个参数,叫着一元谓…...

Arkts深入了解运用 LazyForEach【鸿蒙专栏-17】
文章目录 深入了解 LazyForEach:数据懒加载LazyForEach概述接口描述IDataSource接口DataChangeListener接口使用限制和注意事项键值生成规则和组件创建规则首次渲染键值相同时错误渲染键值生成规则和组件创建规则首次渲染键值相同时错误渲染键值生成规则和组件创建规则首次渲染…...

如何让你的 Jmeter+Ant 测试报告更具吸引力?
引言 想象一下,你辛苦搭建了一个复杂的网站,投入了大量的时间和精力进行开发和测试。当你终于完成了测试并准备生成测试报告时,你可能会发现这个过程相当乏味,而对于其他人来说,它可能也不那么吸引人。 但是…...

游戏APP接入哪些广告类型
当谈到游戏应用程序(APP)接入广告时,选择适合用户体验和盈利的广告类型至关重要。游戏开发者通常考虑以下几种广告类型: admaoyan猫眼聚合 横幅广告: 这些广告以横幅形式显示在游戏界面的顶部或底部。它们不会打断游戏…...

Echarts地图registerMap使用的GeoJson数据获取
https://datav.aliyun.com/portal/school/atlas/area_selector 可以选择省,市,区。 也可以直接在地图上点击对应区域。 我的应用场景 我这里用到这个还是一个特别老的大屏项目,用的jq写的。显示中国地图边界区域 我们在上面的这个地区选择…...

【JavaEE】Java中的多线程 (Thread类)
作者主页:paper jie_博客 本文作者:大家好,我是paper jie,感谢你阅读本文,欢迎一建三连哦。 本文录入于《JavaEE》专栏,本专栏是针对于大学生,编程小白精心打造的。笔者用重金(时间和精力)打造&…...

python中具名元组的使用
collections.namedtuple是一个工厂函数,它可以用来构建一个带字段名的元组和一个有名字的类。 from collections import namedtuple City namedtuple(City2, name country population coordinates) tokyo City(Tokyo, JP, 36.933, (35.689722, 139.691667)) pr…...

【开题报告】基于SpringBoot的婚纱店试妆预约平台的设计与实现
1.选题背景 婚礼是人生中的重要时刻,而试妆是婚礼准备过程中不可或缺的一环。传统的婚纱店试妆预约方式通常需要亲自到店或通过电话预约,这样的方式可能存在一些问题。首先,用户需要花费时间和精力到店进行预约,对于忙碌的现代人…...

Qt 布局讲解及举例
Qt布局是一个用于管理窗口部件位置和大小的机制,它使得开发人员能够轻松地创建可伸缩、可调整大小的界面。在Qt中,布局管理器是一种用于自动调整窗口部件大小的机制,它可以根据窗口大小的变化自动调整部件的位置和大小。 Qt布局管理器通过使…...

【微服务】java 规则引擎使用详解
目录 一、什么是规则引擎 1.1 规则引擎概述 1.2 规则引擎执行过程 二、为什么要使用规则引擎 2.1 使用规则引擎的好处 2.1.1 易于维护和更新 2.1.2 增强应用程序的准确性和效率 2.1.3 加快应用程序的开发和部署 2.1.4 支持可视化和可管理性 2.2 规则引擎使用场景 三、…...
HCIA-Datacom跟官方路线学习
通过两次更换策略。最后找到最终的学习方案,华为ICT官网有对这个路线的学习,hcia基础有这个学习路线,hcip也有目录路线。所以,最后制定学习路线,是根据这个认证的路线进行学习了: 官网课程:课程…...
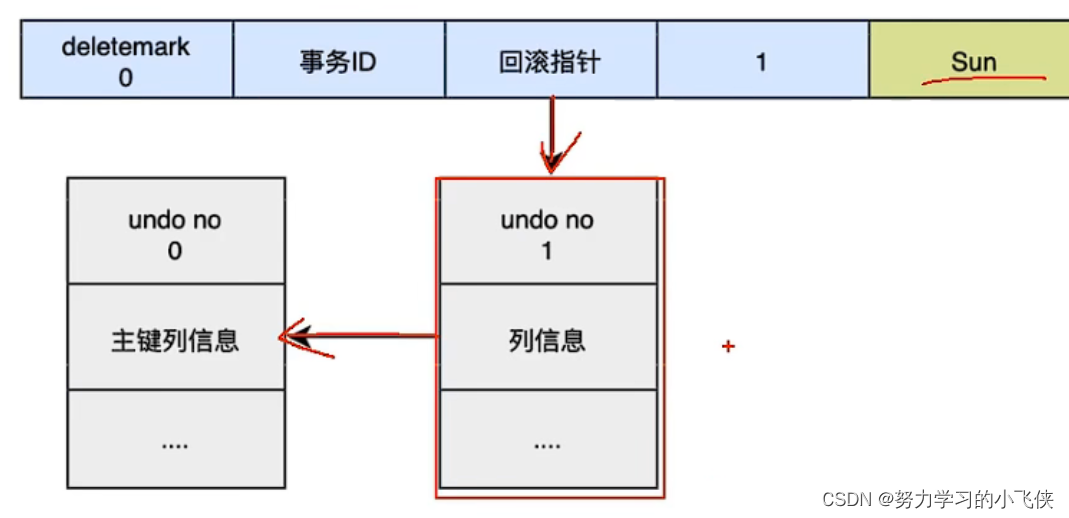
MySQL三大日志详细总结(redo log undo log binlog)
MySQL日志 包括事务日志(redolog undolog)慢查询日志,通用查询日志,二进制日志(binlog) 最为重要的就是binlog(归档日志)事务日志redolog(重做日志)undolog…...
XXL-Job详解(二):安装部署
目录 前言环境下载项目调度中心部署执行器部署 前言 看该文章之前,最好看一下之前的文章,比较方便我们理解 XXL-Job详解(一):组件架构 环境 Maven3 Jdk1.8 Mysql5.7 下载项目 源码仓库地址链接: https://github.…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...
