【数据结构】时间和空间复杂度
马上就要进入到数据结构的学习了 ,我们先来了解一下时间和空间复杂度,这也可以判断我们的算法是否好坏;
如何衡量一个算法的好坏?
就是看它的算法效率
算法效率
算法效率分析分为两种:第一种是时间效率,第二种是空间效率。时间效率被称为时间复杂度,而空间效率被称作空间复杂度。 时间复杂度主要衡量的是一个算法的运行速度,而空间复杂度主要衡量一个算法所需要的额外空间,在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
时间复杂度
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个数学函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
大O的渐进表示法
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
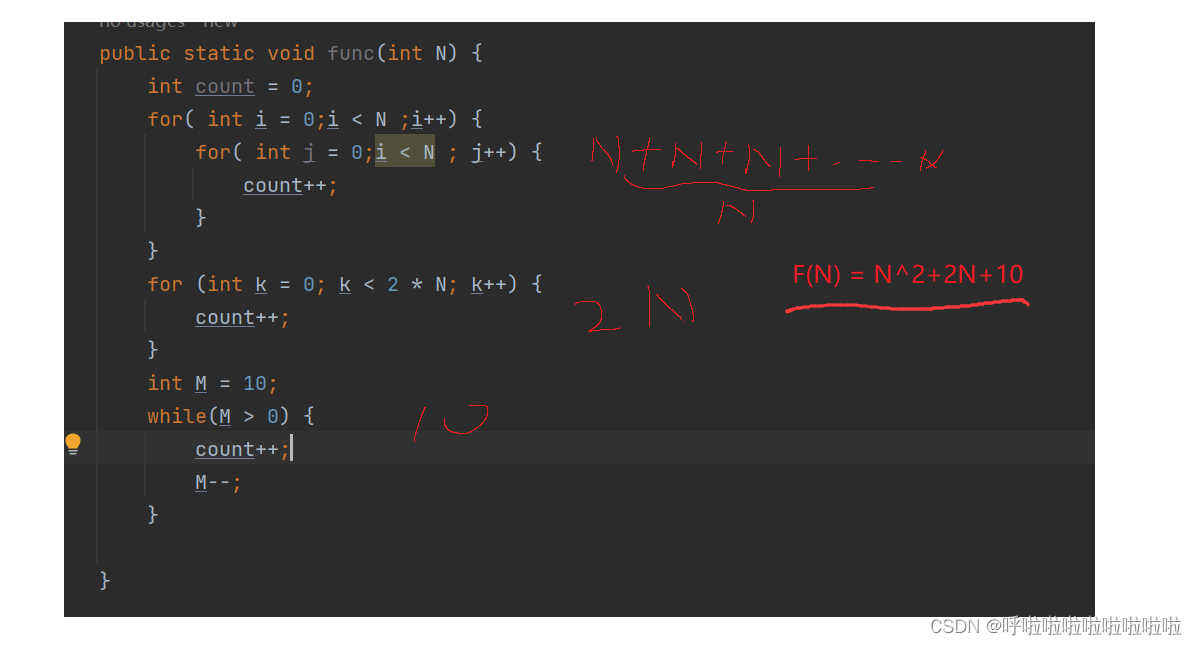
Func 执行的基本操作次数 :
F(N)=N^2+2N+10
但是如果N无限大呢?
N=10 F(N) = 130
N=100 F(N) =10210
N=1000 F(N)=1002010
因此我们有以下结论:
1、用常数1取代运行时间中的所有加法常数。F(N)=N^2+2N+10
2、在修改后的运行次数函数中,只保留最高阶项。F(N)=N^2
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。假如 F(N) = 3N^2
那么3省略 F(N) = N^2
所以 大O为O(N^2)
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
常见时间复杂度计算举例

F(N) = 2N+10
根据公式 F(N)=N;
所以就是O(N)

M和N都为未知数
F(N)=M+N;
所以就是O(M+N)

F(N)=100;
所以F(N)=1;
所以就是O(1);

有最好情况下也有最坏情况下,一般我们只考虑最坏情况下

二分查找的时间复杂度为O(logN)

一般情况下 递归的时间复杂度就为 递归的次数*每次递归执行的次数

这个斐波那契递归得画图分析
所以大O为O(2^N)
空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法

空间复杂度为O(1)
因为没有申请其他的数组,只使用了原来的数组

时间复杂度为O(N)
因为申请了一个其他数组

递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
相关文章:

【数据结构】时间和空间复杂度
马上就要进入到数据结构的学习了 ,我们先来了解一下时间和空间复杂度,这也可以判断我们的算法是否好坏; 如何衡量一个算法的好坏? 就是看它的算法效率 算法效率 算法效率分析分为两种:第一种是时间效率,第…...

【Web】[GKCTF 2021]easycms
直接点击登录按钮没有反应 扫目录扫出来/admin.php 访问 弱口令admin 12345直接登录成功 点开设计--主题--自定义 编辑页头,类型选择php源代码 点保存显示权限不够 设计--组件--素材库 先随便上传一个文件,之后改文件名称为../../../../../system/tmp…...
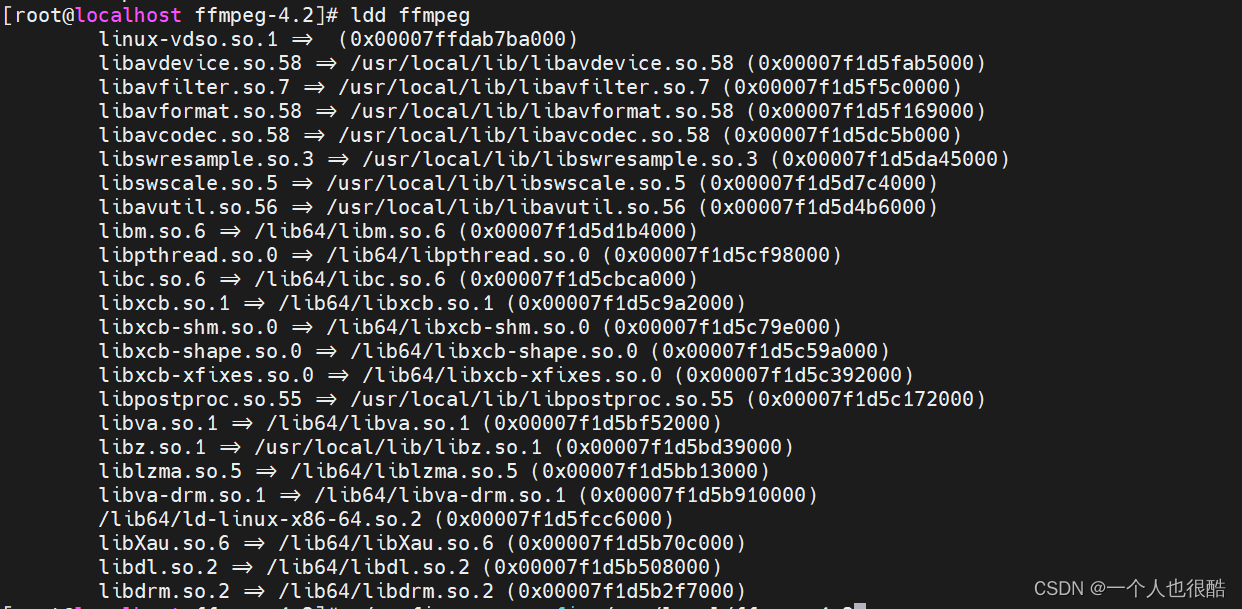
VM CentOS7安装ffmpeg
项目中涉及给视频添加水印,使用到了ffmpeg,windows系统可直接使用,Linux需要手动编译完成ffmpeg后才可正常使用。 配置yum源: 备份原repo文件 cd /etc/yum.repos.d/mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.r…...

PyTorch Models
Overview pth模型保存时是按照“整个模型保存”和“只保存模型参数”会影响模型的加载和访问方式 torch.save(vgg16, "vgg16.pt") torch.save(vgg16,"vgg16.ckpt") torch.save(vgg16,"vgg16.pth") torch.save(vgg16,"vgg16.pkl")…...
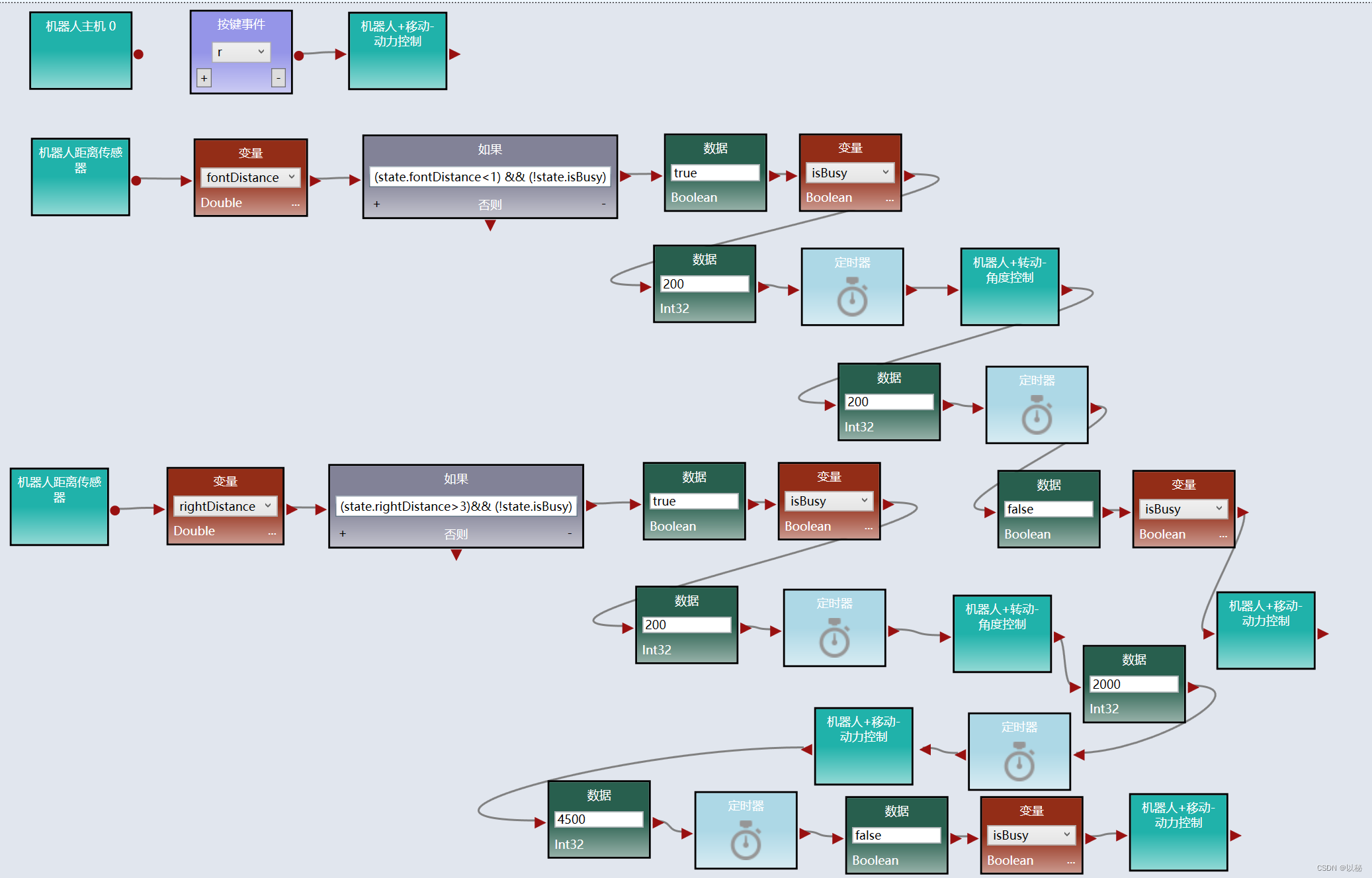
viple模拟器使用(四):unity模拟器中实现沿右墙迷宫算法
沿右墙迷宫算法 引导 线控模拟可以使得通过用户手动操作,实现机器人在模拟环境下在迷宫中行走(即:运动),算法可以使得机器人按照一定的策略自动行走,沿右墙迷宫算法就是其中的一种策略。 目的 运行程序后&…...

面试送分题!“商品分类浏览”如何测试?
电商项目无论是工作中,还是面试中,都是一个高频出现的词。 面试官非常热衷提问关于电商项目的问题。例如商品分类怎么测试?购物车怎么测试?订单怎么测试?优惠券怎么测试?支付怎么测试?等等。 …...

在浏览器中直接打开PDF
1 使用iframe标签 <iframe src"./test.pdf" height"900px;" width"800px"></iframe> 如果PDF是base64参考如下 <iframe id"pdfView" width"100%" height"100%" allow"fullscreen" typ…...

docker集群的详解以及超详细搭建
文章目录 一、问题引入1. 多容器位于同一主机2. 多容器位于不同主机 二、介绍三、特性四、概念1. 节点nodes2. 服务(service)和任务(task)3. 负载均衡 五、docker网络1. overlay网络 六、docker集群搭建1. 环境介绍2. 创建集群3. 集群网络4. 加入工作节点 七、部署可视化界面po…...

4进制思路。。。。。。。。
猪猪 Hanke 特别喜欢吃烤鸡(本是同畜牲,相煎何太急!)Hanke 吃鸡很特别,为什么特别呢?因为他有 1010 种配料(芥末、孜然等),每种配料可以放 11 到 33 克,任意烤…...

解决ansible批量加入新IP涉及known_hosts报错的问题
我们把一批新的IP加入到ansible的hosts文件,比如/etc/ansible/hosts,往往会有这样的提示, 因为本机的~/.ssh/known_hosts文件中并有fingerprint key串,使用ssh连接目标主机时,一般会提示是否将key字符串加入到~/.ssh/…...

vuepress----1、快速开始
创建项目工程 本文会帮助你从头搭建一个简单的 VuePress 文档。如果你想在一个现有项目中使用 VuePress 管理文档,从步骤 3 开始。 创建并进入一个新目录 mkdir vuepress-starter && cd vuepress-starter使用你喜欢的包管理器进行初始化 yarn init # npm i…...
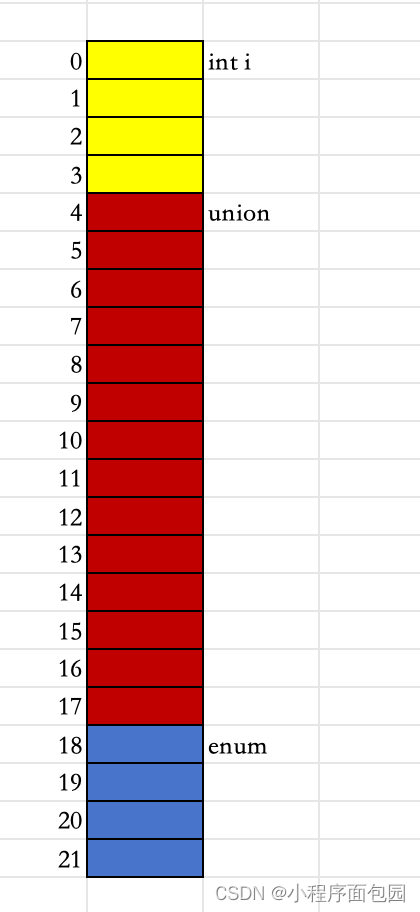
C++ -- 每日选择题 -- Day2
第一题 1. 下面代码中sizeof(A)结果为() #pragma pack(2) class A {int i;union U{char str[13];int i;}u;void func() {};typedef char* cp;enum{red,green,blue}color; }; A:20 B:21 C:22 D:24 答案及解析…...

软件测评中心▏软件集成测试和功能测试之间的区别和联系简析
软件集成测试是在软件开发周期的后期阶段进行的测试活动,旨在验证系统各个组件之间的接口和交互是否正常工作。而功能测试是一种验证软件系统是否按照需求规格说明书所规定的功能进行正确实现的测试。接下来,我们来分别探讨一下软件集成测试和功能测试有…...

Selenium/webdriver介绍以及工作原理
最近在看一些底层的东西。driver翻译过来是驱动,司机的意思。如果将webdriver比做成司机,竟然非常恰当。 我们可以把WebDriver驱动浏览器类比成出租车司机开出租车。在开出租车时有三个角色: 乘客:他/她告诉出租车司机去哪里&…...

HTML5+CSS3+JS小实例:九宫格图片鼠标移入移出方向感知特效
实例:九宫格图片鼠标移入移出方向感知特效 技术栈:HTML+CSS+JS 效果: 源码: 【HTML】 <!DOCTYPE html> <html><head><meta http-equiv="content-type" content="text/html; charset=utf-8"><meta name="viewport&…...
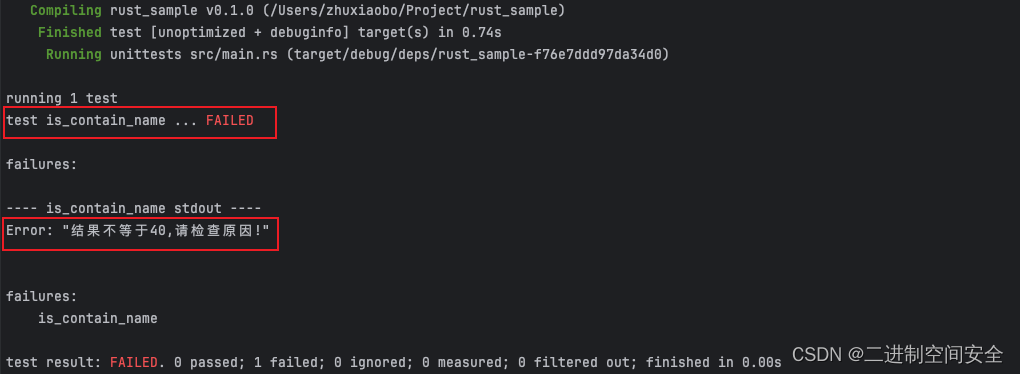
在Rust中编写自动化测试
1.摘要 Rust中的测试函数是用来验证非测试代码是否是按照期望的方式运行的, 测试函数体通常需要执行三种操作:1.设置任何所需的数据或状态;2.运行需要测试的代码;3.断言其结果是我们所期望的。本篇文章主要探讨了Rust自动化测试的几种常见场景。 2.测试函数详解 在Rust项目工…...

羊大师提问,为什么吃得越咸越容易出现健康问题?
羊大师提问,为什么吃得越咸越容易出现健康问题? 在现代社会中,有一种追求咸味食物的趋势,许多人都钟爱于吃咸味食物。吃咸味食物往往容易导致健康问题,引发各种疾病。那么为什么吃的越咸越容易生病呢? 今…...
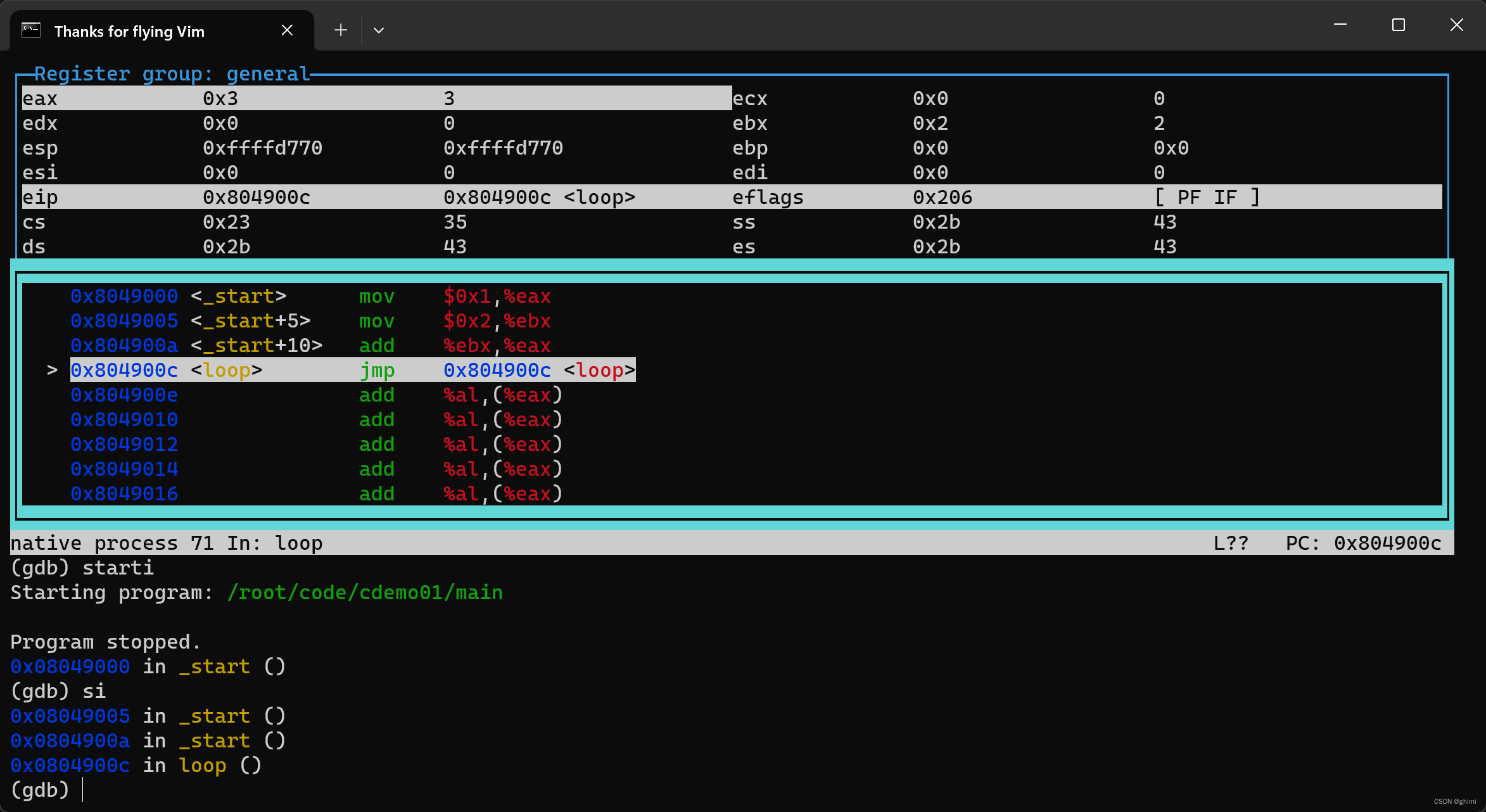
linux ld 链接器学习笔记
ld链接器笔记 1. 首先编写一段汇编代码 这里的汇编语法时 AT&T语法,是gcc原生支持的语法,底层使用 gas(gnu assembler) 完成汇编,相较于 Intel x86语法, AT&T 语法要更加古老,因此大多数人更加偏向于使用 Intel 的语法. nasm 编译器支持x86语法.自从2.10版本…...
)
栈模拟先序后序中序遍历(非递归遍历)
先序遍历: vector<int> preorderTraversal(TreeNode* u) {stack<TreeNode*>stk;vector<int>res;if(unullptr) return res;while(stk.size()||u){if(u){res.push_back(u->val);//遍历当前结点stk.push(u);//记录当前递归层uu->left;//遍历左…...

linux 内核软中断介绍
在介绍软中断之前,先来介绍一个概念:中断下半部: 为了避免处理复杂的中断嵌套,中断处理程序是在关闭中断的情况下执行的。可是,如果关闭中断的时间太长,可能导致中断请求丢失。例如周期时钟每隔 10 毫秒发送…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
