利用MCMC 获得泊松分布
- 写出概率流方程如下
if state == 0: if np.random.random() <= min([Lambda/2, 1]):state = 1else:passelif state == 1:if choose_prob_state[i] <= 0.5:#选择 1 -> 0,此时的接受概率为min[2/Lambda, 1]if np.random.random() <= min([2/Lambda, 1]):state = 0else:passelse:#选择 1 -> 2,此时接受概率为 min[Lambda/(n+1), 1]if np.random.random() <= min([Lambda/(state+1), 1]):state = 2else:passelif state >= 2:if choose_prob_state[i] <= 0.5:#选择 n -> n+1,此时接受概率为 min[Lambda/(n+1), 1]if np.random.random() <= min([Lambda/(state+1), 1]):state = state + 1else:passelse:#选择 n+1 > n,此时接受概率为 min[(n+1)/Lambda, 1]if np.random.random() <= min([(state)/Lambda, 1]):state = state - 1else:pass
- blocking 方法
def block_averages(data, block_size):num_blocks = len(data) // block_sizeblocks = data[:num_blocks*block_size].reshape(num_blocks, block_size)block_avgs = blocks.mean(axis=1)return block_avgsblock_mean = []
block_std = []for i in range(1, 201):block_size = 5 * iblock_avgs = block_averages(results, block_size)mean_estimate = np.mean(block_avgs)standard_error = np.std(block_avgs, ddof=1) / np.sqrt(len(block_avgs))block_mean.append(mean_estimate)block_std.append(standard_error)
- Lambda = 1 生成效果
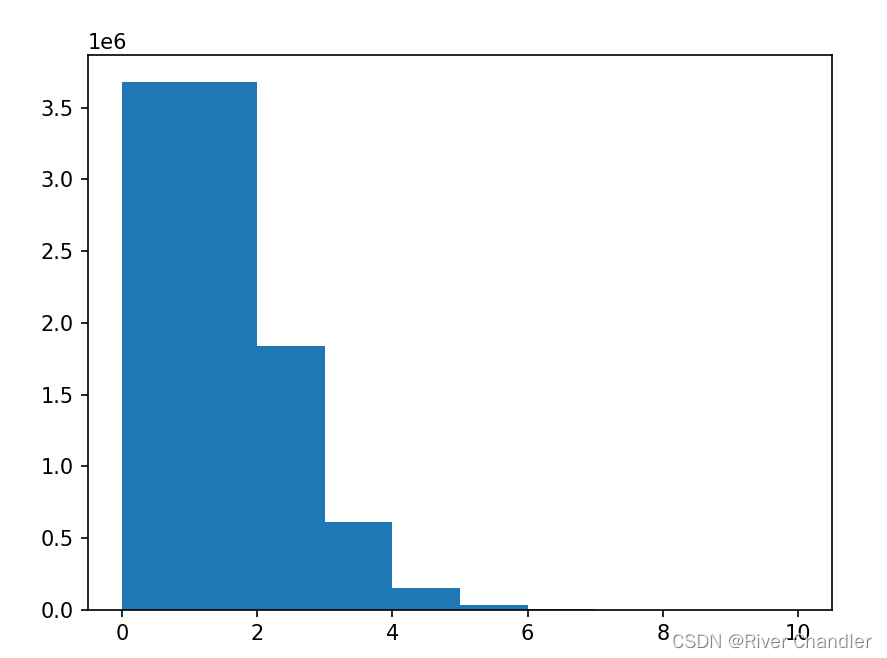
average time: 1.072e-06
ave: 0.9996688
std: 1.00027000870093
(array([3.681131e+06, 3.678446e+06, 1.837276e+06, 6.127200e+05,
1.533770e+05, 3.116400e+04, 5.095000e+03, 7.020000e+02,
8.300000e+01, 6.000000e+00]), array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.]), <BarContainer object of 10 artists>)
- blocking method
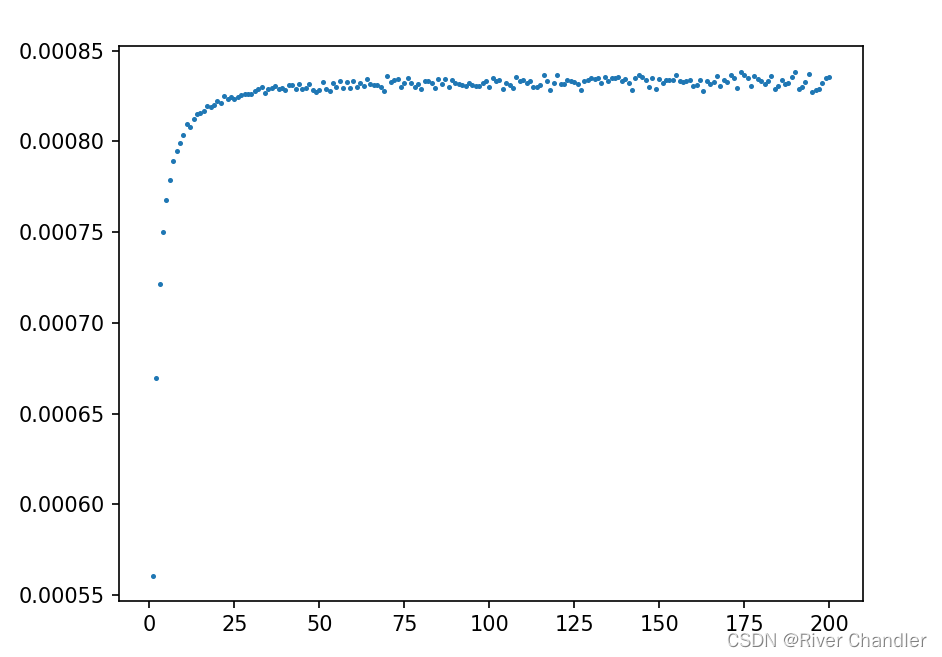
- 随着block 增大 稳定效果显著
- Lambda = 7
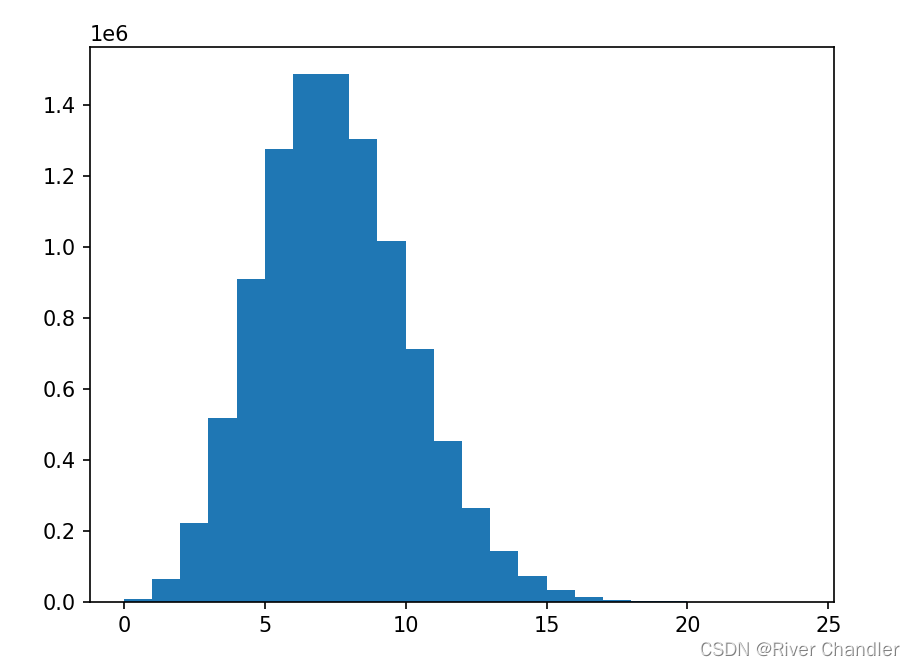
average time: 1.153e-06
ave: 7.0095212
std: 2.6496322285839153
(array([9.062000e+03, 6.352700e+04, 2.216480e+05, 5.190980e+05,
9.097340e+05, 1.274978e+06, 1.487161e+06, 1.487430e+06,
1.304976e+06, 1.016897e+06, 7.126600e+05, 4.541560e+05,
2.646540e+05, 1.432550e+05, 7.228000e+04, 3.374700e+04,
1.474600e+04, 6.073000e+03, 2.455000e+03, 9.640000e+02,
3.790000e+02, 9.900000e+01, 1.700000e+01, 4.000000e+00]), array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11., 12.,
13., 14., 15., 16., 17., 18., 19., 20., 21., 22., 23., 24.]), <BarContainer object of 24 artists>)

- 完整代码
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(20)
import copy
import time##pn = \lambda^n * exp(-\lambda)/n!def poidis(Lambda, num, init=0):random_list = np.zeros(num)state = initmax_state = initrandom_list[0] = statechoose_prob_state = np.random.random(num)for i in range(1, num):if state == 0: if np.random.random() <= min([Lambda/2, 1]):state = 1else:passelif state == 1:if choose_prob_state[i] <= 0.5:#选择 1 -> 0,此时的接受概率为min[2/Lambda, 1]if np.random.random() <= min([2/Lambda, 1]):state = 0else:passelse:#选择 1 -> 2,此时接受概率为 min[Lambda/(n+1), 1]if np.random.random() <= min([Lambda/(state+1), 1]):state = 2else:passelif state >= 2:if choose_prob_state[i] <= 0.5:#选择 n -> n+1,此时接受概率为 min[Lambda/(n+1), 1]if np.random.random() <= min([Lambda/(state+1), 1]):state = state + 1else:passelse:#选择 n+1 > n,此时接受概率为 min[(n+1)/Lambda, 1]if np.random.random() <= min([(state)/Lambda, 1]):state = state - 1else:passelse:print("undefined state!")breakrandom_list[i] = copy.deepcopy(state)if max_state < state:max_state = copy.deepcopy(state)return random_list, max_statenum = int(1e7)
start = time.time()
results, max_state = poidis(7, num)
end = time.time()
print("average time:", round((end-start)/num, 9))hist_doc = plt.hist(results, bins=[i for i in range(max_state+2)])
print("ave:", np.average(results))
print("std:", np.std(results))
print(hist_doc)plt.show()def block_averages(data, block_size):num_blocks = len(data) // block_sizeblocks = data[:num_blocks*block_size].reshape(num_blocks, block_size)block_avgs = blocks.mean(axis=1)return block_avgsblock_mean = []
block_std = []for i in range(1, 201):block_size = 5 * iblock_avgs = block_averages(results, block_size)mean_estimate = np.mean(block_avgs)standard_error = np.std(block_avgs, ddof=1) / np.sqrt(len(block_avgs))block_mean.append(mean_estimate)block_std.append(standard_error)plt.scatter(range(1, 201), block_std, s=2)
plt.show()相关文章:

利用MCMC 获得泊松分布
写出概率流方程如下 if state 0: if np.random.random() < min([Lambda/2, 1]):state 1else:passelif state 1:if choose_prob_state[i] < 0.5:#选择 1 -> 0,此时的接受概率为min[2/Lambda, 1]if np.random.random() < min([2/Lambda, 1]…...
docker-compose脚本编写及常用命令
安装 linux DOCKER_CONFIG/usr/local/lib/docker/cli-plugins sudo mkdir -p $DOCKER_CONFIG/cli-plugins sudo curl -SL https://521github.com/docker/compose/releases/download/v2.6.1/docker-compose-linux-x86_64 -o $DOCKER_CONFIG/cli-plugins/docker-compose sudo c…...

编译企业微信会话内容存档PHP版SDK扩展
1.下载SDK 如果克隆不了,就页面下载 git clone https://github.com/pangdahua/php7-wxwork-finance-sdk2.下载企微官网C版本的最新sdk文件 下载地址:https://wwcdn.weixin.qq.com/node/wework/images/sdk_20201116.rar 下载以后将解压之后的文件夹里l…...

传统算法:使用 Pygame 实现K-Means 聚类算法
使用 Pygame 模块演示了 K-Means 聚类算法的基本原理。让我逐步解释它的实现: 初始化和基本设置 Pygame 初始化: 通过 pygame.init() 初始化 Pygame。 定义颜色和屏幕大小: 定义了一些颜色常量(WHITE, BLACK, RED, GREEN, BLUE)和屏幕的宽度和高度。 创建 Pygame 窗口:…...
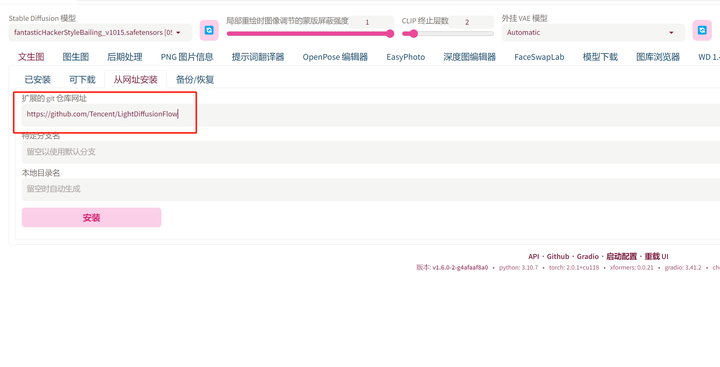
WebUI工作流插件超越ComfyUI
在AI绘画领域,Stable Diffsion是最受欢迎的,因为它是开源软件。 开源有两大优势,一是免费,二是适合折腾。 大量的开发者、爱好者投入无尽的热情,来推动Stable Diffsion的快速发展。 在图形界面方面,WebU…...

Docker容器化平台及其优势和应用场景介绍
Docker是一种开源的容器化平台,它基于操作系统级别虚拟化技术,可以将应用程序及其依赖项打包成一个独立的容器,提供轻量级、一致性、可移植性的应用环境。Docker的基本概念和优势如下: 镜像(Image):Docker容器的基础&…...

Hive:从HDFS回收站恢复被删的表
场景 一张手工维护的内部表,本来排查没有使用,然后删掉了,发现又需要使用,只能恢复这张表了。 1.确认HDFS是否开启回收站功能 2.查看回收站中的数据 被删除的数据会放在删除数据时使用的用户目录下,如:使…...

TZOJ 1387 人见人爱A+B
答案: #include <stdio.h> void time(int ah, int am, int as, int bh, int bm, int bs, int* sum_h, int* sum_m, int* sum_s) //不需要返回值所以定义void函数,前面6个为输入,然后用指针存给后面三个 {*sum_s (as bs) % 60; …...
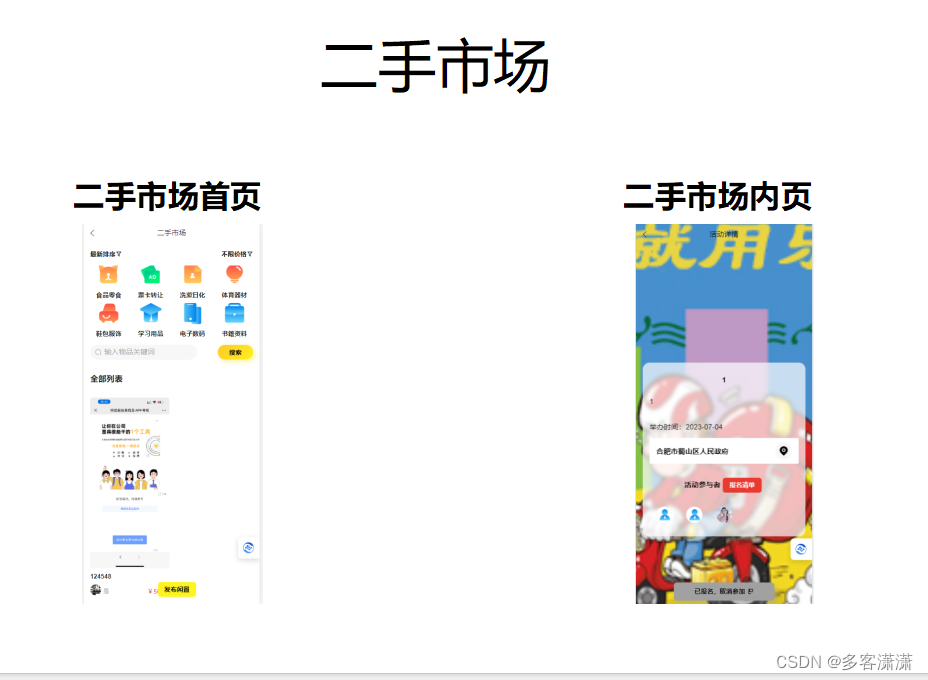
校园圈子系统丨交友丨地图找伴丨二手市场等功能丨源码交付支持二开丨APP小程序H5三端交付!
校园圈子系统是一款专为校园生活设计的智能应用,拥有丰富多样的功能模块,提供全方位的服务。无论您是师生还是校友,我们都为您打造了一个与校园紧密相连的交流平台。 通过校园圈子系统,您可以方便地浏览校内最新动态,包…...

java操作windows系统功能案例(一)
下面是一个Java操作Windows系统功能的简单案例: 获取系统信息: import java.util.Properties;public class SystemInfo {public static void main(String[] args) {Properties properties System.getProperties();properties.list(System.out);} }该程…...

【双向链表的实现】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 1. 双向链表的结构 2. 双向链表的实现 2.1 头文件 ——双向链表的创建及功能函数的定义 2.2 源文件 ——双向链表的功能函数的实现 2.3 源文件 ——双向链表功能的…...

中台战略思想与架构总结
中台战略思想与架构总结 在2015年年中,马云带领阿里高管,拜访了游戏公司Supercell,以《部落战争》《海岛奇兵》《卡通农场》等游戏知名。 Supercell是一家典型的以小团队模式进行游戏开发的公司,一般来说两个员工,或…...
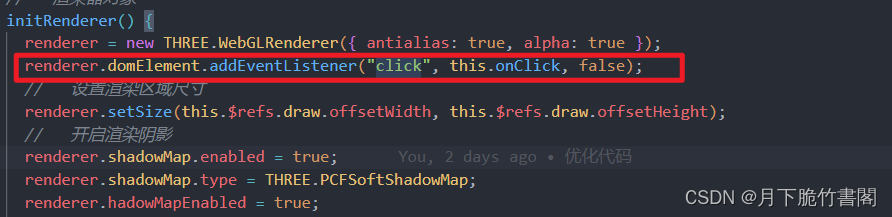
VUE2+THREE.JS点击事件
THREE.JS点击事件 1.增加监听点击事件2.点击事件实现3.记得关闭页面时 销毁此监听事件 1.增加监听点击事件 renderer.domElement.addEventListener("click", this.onClick, false); 注:初始化render时监听 2.点击事件实现 onClick(event) {const raycaster new …...

基于SSM+SpringBoot+Vue小区车位租赁系统
[技术实现] 小区车位租赁系统是使用SSMSpringBootVue前后端分离的管理系统。使用Spring框架可以在自动注入项目层级之间的调用对象,方便解耦,SpringMVC是体现了MVC设计思想的轻量级web框架,对web层进行解耦,使开发更简洁,MyBatis…...

Oracle(2-8)Configuring the Database Archiving Mode
文章目录 一、基础知识1、Redo Log History2、NOARCHIVELOG Mode 非归档模式3、ARCHIVELOG Mode 归档模式4、Changing the Archiving Mode 更改归档模式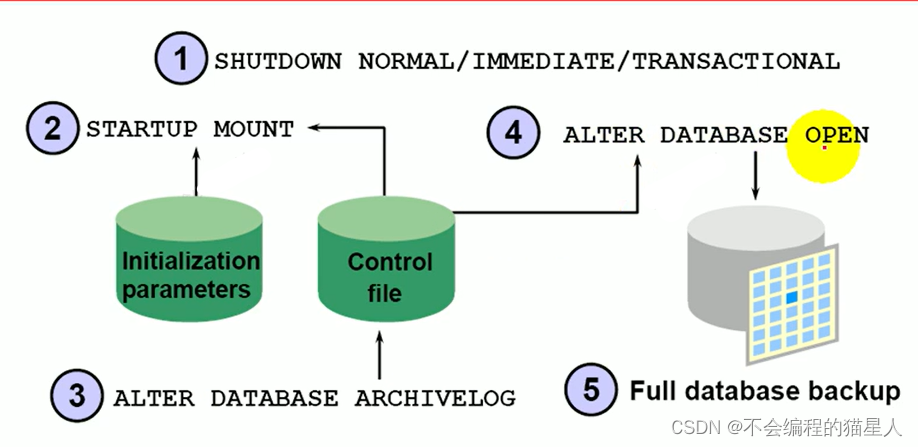5、Auto and Manual Ar…...

制造企业建设数字工厂管理系统的难点主要有哪些
随着科技的飞速发展,制造企业正面临着从传统生产模式向数字化、智能化转型的挑战。其中,建设数字工厂管理系统是实现这一目标的重要途径。然而,在实际操作过程中,制造企业往往会遇到一系列难点。本文将对这些难点进行详细的分析。…...

基于UDP网络聊天室OICQ
Linux系统 Gcc Gdb makefile 实现局域网OICQ程序设计,包括客户端和服务端。 客户端描述:客户端运行开始出现登陆界面。与服务端进行连接,连接后把账号信息发送给服务端,服务端验证后,把确认结果通知客户端。如果通…...
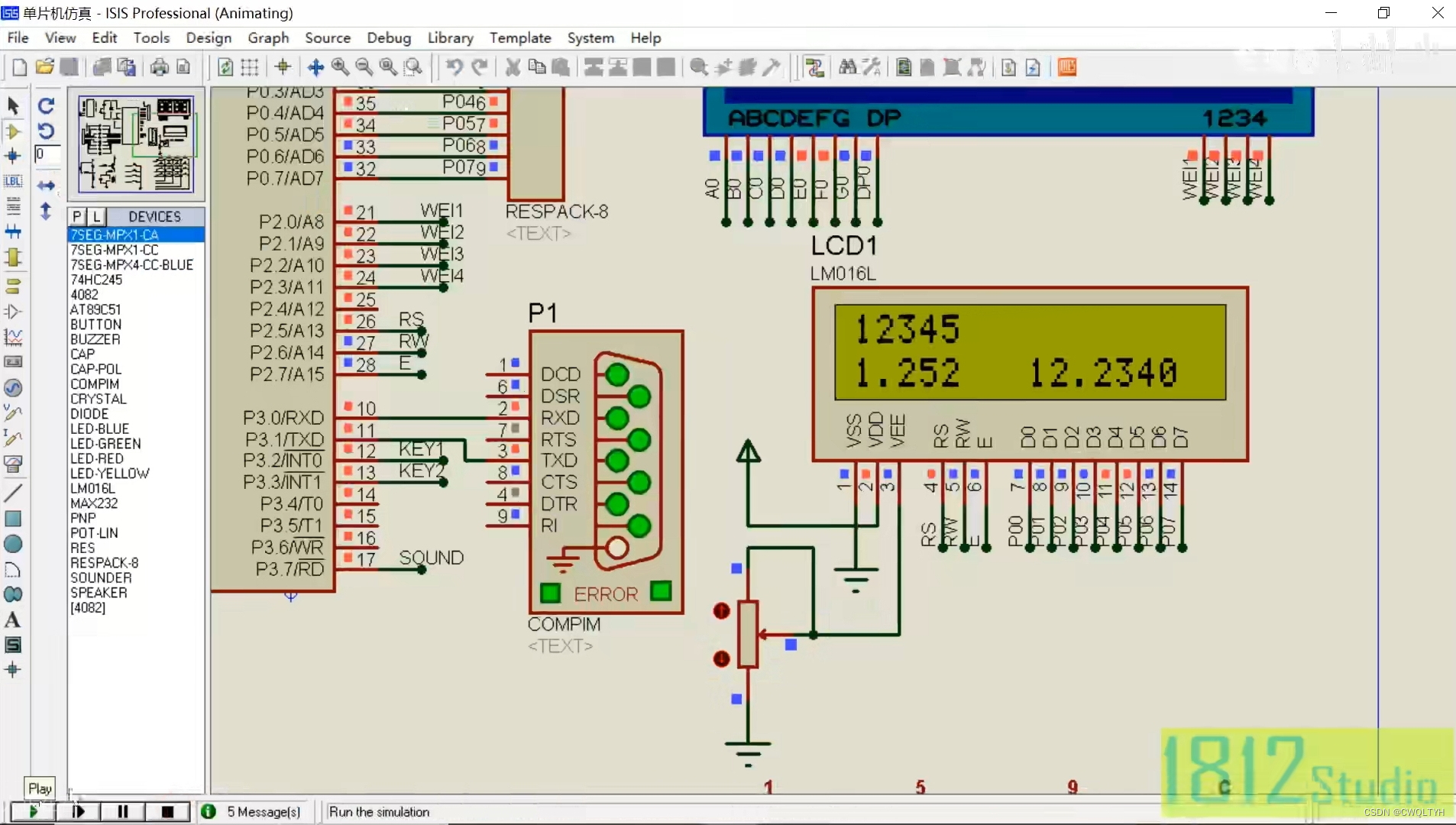
基于STC12C5A60S2系列1T 8051单片机的液晶显示器LCD1602显示整数、小数应用
基于STC12C5A60S2系列1T 8051单片机的液晶显示器LCD1602显示整数、小数应用 STC12C5A60S2系列1T 8051单片机管脚图STC12C5A60S2系列1T 8051单片机I/O口各种不同工作模式及配置STC12C5A60S2系列1T 8051单片机I/O口各种不同工作模式介绍液晶显示器LCD1602简单介绍IIC通信简单介绍…...

【微信小程序】保存多张图片到本地相册 wx.saveImageToPhotosAlbum
这里写目录标题 微信小程序检测是否有存储权限wx.getSetting 图片上传从HTML中提取img标签的src属性多图片下载 微信小程序检测是否有存储权限 wx.getSetting 上传前判断是否开启存储权限,如果不检测直接上传会出现fail的情况 var _this this wx.getSetting({su…...
【Android】使用intent.putExtra()方法在启动Activity时传递数据
食用方法 在Android中,你可以使用Intent对象来在启动Activity时传递数据。以下是一个示例,展示了如何在startActivity时传递数据到被启动的Activity: 在启动Activity的地方,创建一个Intent对象,并使用putExtra()方法…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
