【管理运筹学】背诵手册(六)| 图与网络分析(最大流问题,最小费用最大流问题)
六、图与网络分析
最大流问题
最大流问题的数学规划模型为: max v = f 12 + f 13 { f 12 + f 13 − f 57 − f 67 = 0 f 13 + f 23 = f 34 + f 35 . . . 0 ≤ f i j ≤ c i j \max v=f_{12}+f_{13}\\ \begin{cases} f_{12}+f_{13}-f_{57}-f_{67}=0 \\ f_{13}+f_{23}=f_{34}+f_{35} \\ ...\\ 0\leq f_{ij}\leq c_{ij} \end{cases} maxv=f12+f13⎩ ⎨ ⎧f12+f13−f57−f67=0f13+f23=f34+f35...0≤fij≤cij 第一个约束表示从起点流出的流量等于流入终点的流量;最后一个为容量限制条件;中间的约束为中间点的平衡条件。
满足容量限制条件和平衡条件(起点、终点和中间点)的网络流称为可行流,可行流总是存在的,如零流。
定义网络 G G G 中的一条初等链 μ \mu μ(所有顶点均不相同),方向为从起点到终点,若链上有弧与 μ \mu μ 方向一致,称为前向弧;若有弧与 μ \mu μ 的方向相反,称为后向弧。网络中 f i j = c i j f_{ij}=c_{ij} fij=cij 的弧称为饱和弧, f i j < c i j f_{ij}<c_{ij} fij<cij 的弧称为非饱和弧, f i j = 0 f_{ij}=0 fij=0 的弧称为零流弧。
若某条链中所有前向弧非饱和,后向弧非零,称其为一条增广链。
可行流为最大流的充要条件是不存在增广链。
从起点 v s v_s vs 到终点 v t v_t vt 的最大流的流量,等于分离 v s , v t v_s,v_t vs,vt 的最小截集的容量。
寻找最大流的标号法,称为 2F 算法。可分为两个过程,一是标号过程,二是调整过程。
标号过程先给起点标上 ( 0 , + ∞ ) (0,+\infty) (0,+∞) ,若在前向弧 ( v i , v j ) (v_i,v_j) (vi,vj) 上, f i j < c i j f_{ij}<c_{ij} fij<cij ,则给 v j v_j vj 标号 ( v s , l ( v j ) ) (v_s,l(v_j)) (vs,l(vj)) ,其中 l ( v j ) = min { l ( v i ) , c i j − f i j } l(v_j)=\min\{l(v_i),c_{ij}-f_{ij}\} l(vj)=min{l(vi),cij−fij} ;若在后向弧 ( v j , v i ) (v_j,v_i) (vj,vi) 上, f i j > 0 f_{ij}>0 fij>0 ,则给 v j v_j vj 标号 ( − v i , l ( v j ) ) (-v_i,l(v_j)) (−vi,l(vj)) ,其中 l ( ( v j ) = min { l ( v i ) , f i j } l((v_j)=\min\{l(v_i),f_{ij}\} l((vj)=min{l(vi),fij} 。
调整过程的调整量为终点的标号,令前向弧加上这个调整量,后向弧减去这个调整量。
当出现有多个收发点时,可以虚拟一个总发点和总收点或把所有收发点看成一个整体,先解决外部的流量分配,再解决整体内部的流量分配。当网络为无向图时,可以考虑用枚举法用最小截求最大流。标准的最大流问题应只有弧有容量限制,当出现某个节点也有容量限制时,应进行转换,将其分为两个节点 λ , μ \lambda,\mu λ,μ 。原来流入的弧全部连接到 λ \lambda λ ,原来流出的点全部从 μ \mu μ 节点流出。
最小费用流
链的费用为链中前向弧的费用减去后向弧的费用。所有增广链中费用最小的链称为最小费用增广链。
定理:若 f f f 是流量为 V ( f ) V(f) V(f) 的最小费用流, μ \mu μ 是关于 f f f 的从 v s v_s vs 到 v t v_t vt 的一条最小费用增广链,则 f f f 经过 μ \mu μ 调整流量后得到新的可行流 f ′ f' f′ , f ′ f' f′ 一定是流量为 V ( f ) + θ V(f)+\theta V(f)+θ 的可行流中的最小费用流。
因此我们可以从某个初始的最小费用可行流(一般为零流)开始,寻找最小费用增广链,然后按照最大流的标号法,不断调整到目标流量。
初始的可行流好找,题目给了就用题目的,没给就用零流。那最小费用增广链怎么找?如果把每条弧的费用看成权,这就相当于求起点到终点的最短路。但是由于增广链中可能还有后向弧,无法直接利用最短路算法,因此需要构造一个有向网络 L ( f ) L(f) L(f) 。
构造的方法为:顶点仍然是原网络中的顶点,原来的每条弧变成两个方向相反的弧,正向弧如果非饱和,权重为费用 w i j w_{ij} wij ,否则为无穷;后向弧如果非零,权重为 − w i j -w_{ij} −wij ,否则为无穷。而权重为无穷的弧我们一般会省略。
根据初始可行流,我们构造一个网络,找起终点的最短路,在这条最小费用增广链上按照最大流算法调整,得到新流。根据新流又可以构造网络,如此循环。当出现找不到最短路时,说明已经达到最大流,如果此时的流量仍然小于目标流量,说明不存在流量为目标流量的最小费用流。
最小费用最大流
此时没有目标流量的要求,因此要一直寻找最短路,直到找不到为止。
相关文章:
| 图与网络分析(最大流问题,最小费用最大流问题))
【管理运筹学】背诵手册(六)| 图与网络分析(最大流问题,最小费用最大流问题)
六、图与网络分析 最大流问题 最大流问题的数学规划模型为: max v f 12 f 13 { f 12 f 13 − f 57 − f 67 0 f 13 f 23 f 34 f 35 . . . 0 ≤ f i j ≤ c i j \max vf_{12}f_{13}\\ \begin{cases} f_{12}f_{13}-f_{57}-f_{67}0 \\ f_{13}f_{23}f_{34}f…...

C语言之结构体详解
C语言之结构体详解 文章目录 C语言之结构体详解1. 结构体类型的声明2. 结构体变量的创建和初始化3. 结构体的特殊声明4. 结构体的自引用结构体的自引用匿名结构体的自引用 5. 结构体内存对齐5.1 练习一5.2 练习三 6. 为什么存在内存对⻬? 1. 结构体类型的声明 struct tag {me…...

学习canvas
Canvas是一个基于像素的渲染引擎,它使用JavaScript API在画布上绘制图像。以下是它的一些优点和缺点: 优点: Canvas的渲染速度快,适合处理大量图像和高度动态的图像。 可以直接操作像素,从而能够创建出高质量、流畅的…...

浏览器的渲染原理
以下内容来源于渡一前端大师课,仅作个人学习记录。 渲染的第一步是 解析HTML 解析过程中遇到CSS解析CSS,遇到JS执行JS。为了提高解析效率,浏览器在开始解析之前,会启动一个预解析的线程,率先下载HTML中的外部CSS文件和…...

从 JSON 转 Java 实体的多种方法详解
将 JSON 数据转换为 Java 对象是现代应用程序开发中常见的任务。在 Java 中,有多种方法可以实现这一目标。本文将详细介绍几种常见的方法,以及它们的优缺点。 1. 手动映射(Manual Mapping) 手动映射是最基础的方法之一ÿ…...
数据库的多表查询(MYSQL)表表联立
根据以上三张表格,对三张表格进行不同的联立,查询并显示符合条件的内容。 1. 查出至少有一个员工的部门。显示部门编号、部门名称、部门位置、部门人数。 mysql> SELECT d.deptno AS 部门编号, d.dname as 部门名称, d.loc as 部门位置, COUNT(e.emp…...
)
P8650 [蓝桥杯 2017 省 A] 正则问题(dfs )
多重括号,利用回溯来对上一层括号中的内容进行反馈 实现: 若为 x 长度加一 若为 ( 进入递归计算 (计算相当于子表达式) 若为 ) 结束当前递归 若为 | …...

【ESP32】手势识别实现笔记:红外温度阵列 | 双三次插值 | 神经网络 | TensorFlow | ESP-DL
目录 一、开发环境搭建与新建工程模板1.1、开发环境搭建与卸载1.2、新建工程目录1.3、自定义组件 二、驱动移植与应用开发2.1、I2C驱动移植与AMG8833应用开发2.2、SPI驱动移植与LCD应用开发2.3、绘制温度云图2.4、启用PSRAM(可选)2.5、画面动静和距离检测…...
No matching version found for @babel/compat-data@^7.23.5 处理
npm ERR! notarget No matching version found for babel/compat-data^7.23.5 处理 报错信息 npm WARN ERESOLVE overriding peer dependency npm ERR! code ETARGET npm ERR! notarget No matching version found for babel/compat-data^7.23.5. npm ERR! notarget In most …...

手持机|三防智能手机_4寸/5寸/6寸安卓系统三防手机PDA手持终端方案
随着科技的不断发展,三防手持机作为一种多功能设备,正逐渐在各行业得到广泛应用。这款手持机采用高性能处理器,支持高精度北斗定位和工业本安防爆功能,并具备IP67级防水防尘性能和1.5米防跌落能力。因此,它在仓储管理、…...

蓝桥杯算法心得——仙界诅咒(dfs)
大家好,我是晴天学长,搜索型的dfs,差点开二维矩阵了,仔细一想,没那么夸张啊,哈哈哈,需要的小伙伴可以关注支持一下哦!后续会继续更新的。💪💪💪 1…...
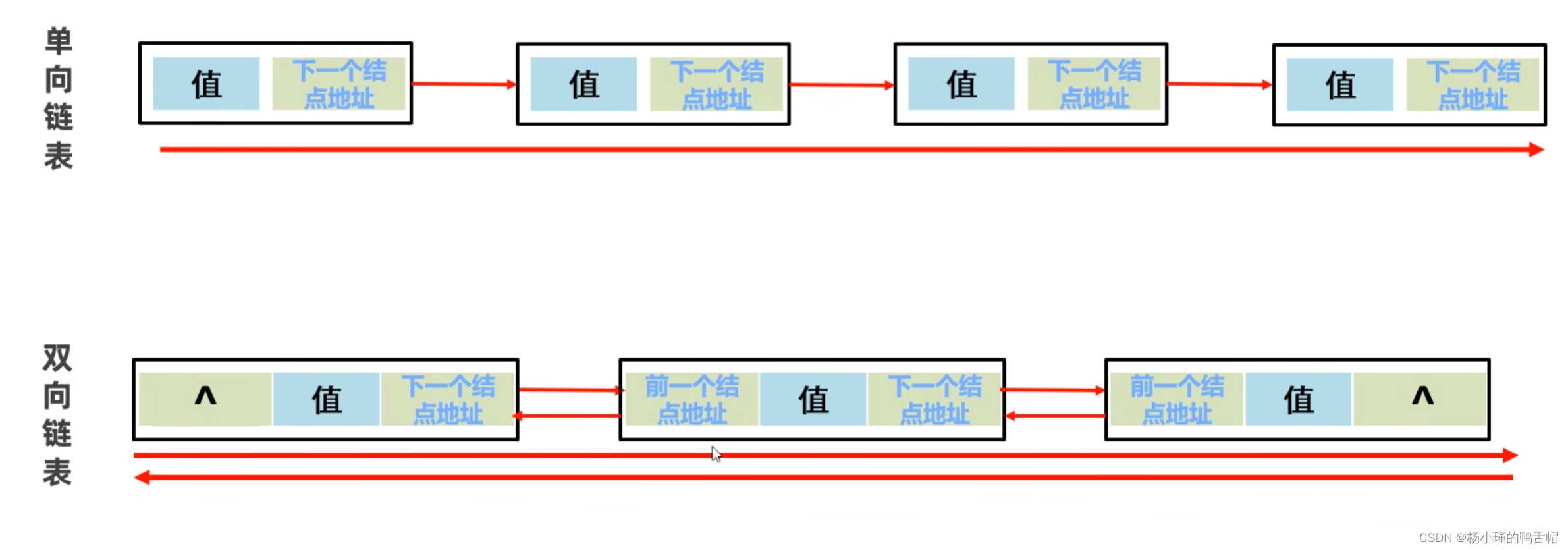
List集合,遍历,数据结构
一.List常见的方法: 二. List集合的遍历方式 除了 迭代器遍历 增强for遍历 Lambda表达式遍历,还有自己独有的普通for遍历,列表迭代器遍历 1.迭代器遍历 2.增强for遍历 3.Lambda表达式遍历 4.普通for遍历 5.列表迭代器遍历 列表迭代器相对于…...

2的幂运算
2的幂 描述 : 给你一个整数 n,请你判断该整数是否是 2 的幂次方。如果是,返回 true ;否则,返回 false 。 如果存在一个整数 x 使得 n 2x ,则认为 n 是 2 的幂次方。 题目 : LeetCode 231.2的幂 : 231. 2 的幂 分…...

优先队列经典例题leetcode思路代码详解
目录 leetcode215题.数组中的第k个最大元素 leetcode347题.前k个高频元素 leetcode295题.数据流的中位数 对优先队列感兴趣的朋友可以去看我上一篇文章。 优先队列基础讲解-CSDN博客 leetcode215题.数组中的第k个最大元素 215. 数组中的第K个最大元素 - 力扣(…...

新型Python环境与依赖管理工具——pipenv
文章目录 pipenv介绍pipenv安装pipenv使用创建虚拟环境删除虚拟环境安装依赖查看包之间的依赖图卸载依赖在虚拟环境中执行命令shell环境下通过requirements.txt安装依赖导出requirements.txt文件查看虚拟环境的路径 pipenv介绍 pipenv可以看做是pip和virtualenv的组合体&#…...
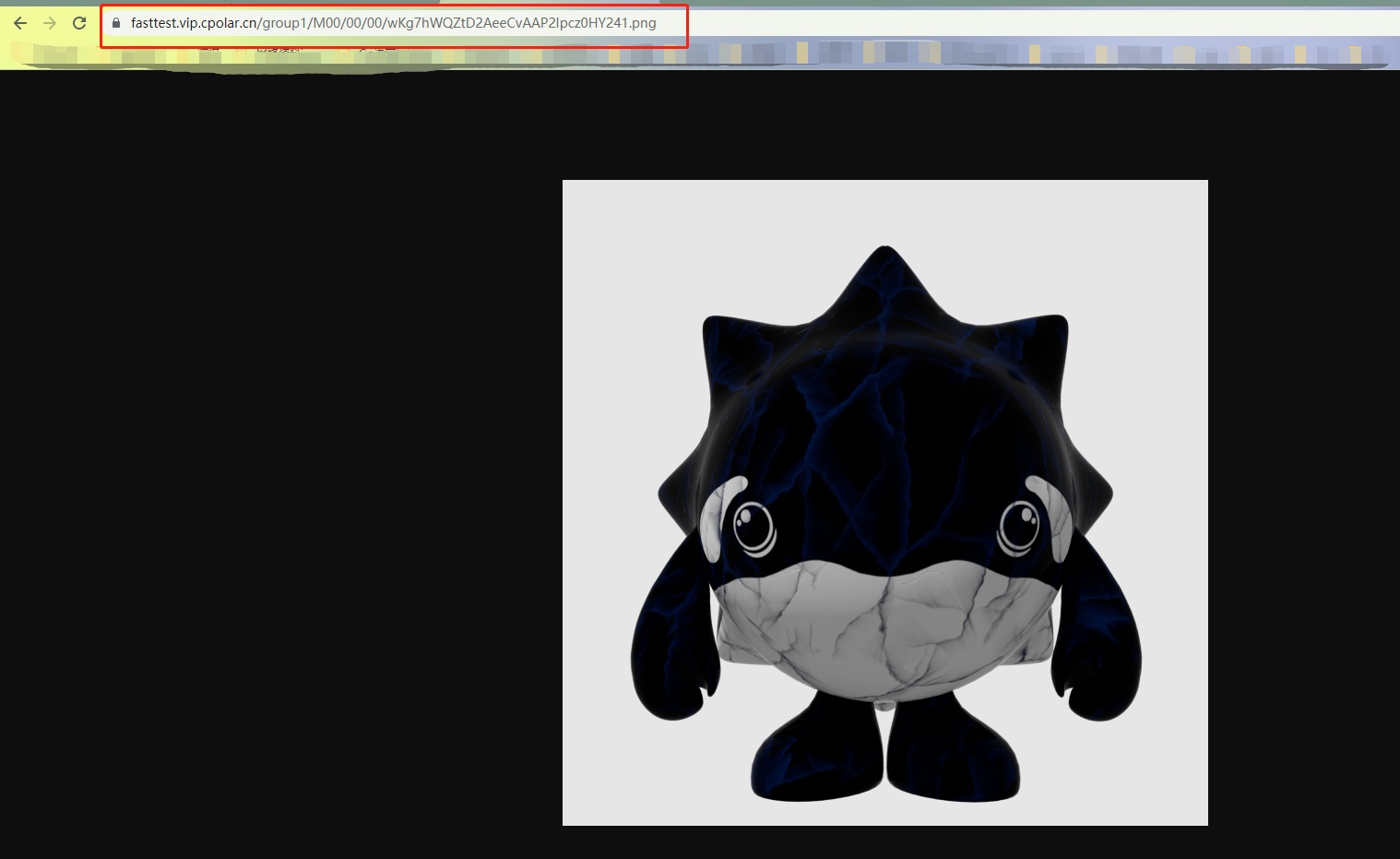
FastDFS+Nginx - 本地搭建文件服务器同时实现在外远程访问「内网穿透」
文章目录 前言1. 本地搭建FastDFS文件系统1.1 环境安装1.2 安装libfastcommon1.3 安装FastDFS1.4 配置Tracker1.5 配置Storage1.6 测试上传下载1.7 与Nginx整合1.8 安装Nginx1.9 配置Nginx 2. 局域网测试访问FastDFS3. 安装cpolar内网穿透4. 配置公网访问地址5. 固定公网地址5.…...

kendo-splitter动态分配分隔框大小
通过size方法,动态改变框大小,参考链接:https://docs.telerik.com/kendo-ui/api/javascript/ui/splitter/methods/size vue画面 <kendo-button type"primary" click"changePane">button</kendo-button><…...

网站提示不安全?
随着互联网的普及和发展,网络安全问题日益严重。黑客攻击、数据泄露、恶意软件等问题层出不穷,给企业和个人带来了巨大的损失。在这个背景下,确保网站安全显得尤为重要,而使用SSL证书是解决这些问题的有效措施。 什么是SSL证书&am…...

C# 泛型编译特性对性能的影响
C#作为一种强类型语言,具有丰富的泛型支持,允许开发者编写可以应对不同数据类型的通用代码。然而,在泛型编译时,针对结构和类作为泛型参数时,会对性能产生不同的影响。 泛型编译行为 在C#中,泛型编译行为取…...
11-30 JavaWeb
修改与删除操作 防止空指针异常 localhost:8080 -> 分页查询 修改流程:(先查后改(两个servlet)) 修改: 传用户id(用户id怎么得到 -> 循环一次得到一个user 对象 user对象里用user.getId()得到用户id) UpdateUserQueryServlet.java (…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
