AcWing算法提高课-3.1.2信使
宣传一下算法提高课整理 <—
CSDN个人主页:更好的阅读体验 <—

题目传送门点这里
题目描述
战争时期,前线有 nnn 个哨所,每个哨所可能会与其他若干个哨所之间有通信联系。
信使负责在哨所之间传递信息,当然,这是要花费一定时间的(以天为单位)。
指挥部设在第一个哨所。
当指挥部下达一个命令后,指挥部就派出若干个信使向与指挥部相连的哨所送信。
当一个哨所接到信后,这个哨所内的信使们也以同样的方式向其他哨所送信。信在一个哨所内停留的时间可以忽略不计。
直至所有 nnn 个哨所全部接到命令后,送信才算成功。
因为准备充足,每个哨所内都安排了足够的信使(如果一个哨所与其他 k 个哨所有通信联系的话,这个哨所内至少会配备 kkk 个信使)。
现在总指挥请你编一个程序,计算出完成整个送信过程最短需要多少时间。
输入格式
第 111 行有两个整数 nnn 和 mmm,中间用 111 个空格隔开,分别表示有 nnn 个哨所和 mmm 条通信线路。
第 222 至 m+1m+1m+1 行:每行三个整数 i、j、ki、j、ki、j、k,中间用 111 个空格隔开,表示第 iii 个和第 jjj 个哨所之间存在 双向 通信线路,且这条线路要花费 kkk 天。
输出格式
一个整数,表示完成整个送信过程的最短时间。
如果不是所有的哨所都能收到信,就输出-1。
数据范围
1≤n≤100,1≤n≤100,1≤n≤100,
1≤m≤200,1≤m≤200,1≤m≤200,
1≤k≤10001≤k≤10001≤k≤1000
样例输入
4 4
1 2 4
2 3 7
2 4 1
3 4 6
样例输出
11
题目化简:
给定一个 nnn 个点 mmm 条边的无向图,求编号为1的点与其他点之间最短距离的最大值。
思路
这道题因为数据范围极小,为了节约代码长度,可以采用Floyd算法。
在求出任意两点间最短距离之后,遍历dist[1][i],求出最大值。
Dijkstra算法与Floyd类似,代码部分也给出了朴素Dijkstra和堆优化Dijkstra的代码。
算法时间复杂度
如果采用Floyd算法,那么时间复杂度是O(n3)O(n^3)O(n3);
朴素Dijkstra算法:O(n2)O(n^2)O(n2), 但是代码较长;
堆优化Dijkstra算法:O(mlogn)O(m \log n)O(mlogn),同样的代码较长
AC Code
C++(Floyd)C++ (Floyd)C++(Floyd)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 110, inf = 1e9;int n, m;
int d[N][N];void init()
{for (int i = 1; i <= n; i ++ )for (int j = 1; j <= n; j ++ )if (i == j) d[i][j] = 0;else d[i][j] = inf;
}void floyd()
{for (int k = 1; k <= n; k ++ )for (int i = 1; i <= n; i ++ )for (int j = 1; j <= n; j ++ )d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}int main()
{cin >> n >> m;init();while (m -- ){int a, b, c;cin >> a >> b >> c;d[a][b] = min(d[a][b], c);d[b][a] = min(d[b][a], c);}floyd();int res = 0;for (int i = 2; i <= n; i ++ )res = max(res, d[1][i]);if (res == inf) puts("-1");else printf("%d\n", res);return 0;
}
C++(朴素Dijkstra)C++ (朴素Dijkstra)C++(朴素Dijkstra)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 110;int n, m;
int g[N][N];
int dist[N];
bool st[N];int dijkstra()
{int res = 0;memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 1; i <= n; i ++ ){int t = -1;for (int j = 1; j <= n; j ++ )if (!st[j] &&(t == -1 || dist[t] > dist[j]))t = j;st[t] = true;res = max(res, dist[t]);for (int j = 1; j <= n; j ++ )dist[j] = min(dist[j], dist[t] + g[t][j]);}return res == 0x3f3f3f3f ? -1 : res;
}
int main()
{memset(g, 0x3f, sizeof g);scanf("%d%d", &n, &m);while (m -- ){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = g[b][a] = min(g[a][b], c);}cout << dijkstra() << endl;return 0;
}
C++(堆优化Dijkstra)C++ (堆优化Dijkstra)C++(堆优化Dijkstra)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>#define x first
#define y secondusing namespace std;typedef pair<int, int> PII;const int N = 110, M = N << 2;int n, m;
int h[N], e[M], w[M], ne[M], idx;
int dist[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int dijkstra()
{int res = 0, cnt = 0;memset(dist, 0x3f, sizeof dist);dist[1] = 0;priority_queue<PII, vector<PII>, greater<>> heap;heap.push({0, 1});while (!heap.empty()){PII u = heap.top();heap.pop();if (st[u.y]) continue;st[u.y] = true;res = max(res, u.x);cnt ++ ;for (int i = h[u.y]; ~i; i = ne[i]){int j = e[i];if (dist[j] > dist[u.y] + w[i]){dist[j] = dist[u.y] + w[i];heap.push({dist[j], j});}}}return cnt == n ? res : -1;
}
int main()
{memset(h, -1, sizeof h);scanf("%d%d", &n, &m);while (m -- ){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c), add(b, a, c);}cout << dijkstra() << endl;return 0;
}

最后,如果觉得对您有帮助的话,点个赞再走吧!
相关文章:

AcWing算法提高课-3.1.2信使
宣传一下算法提高课整理 <— CSDN个人主页:更好的阅读体验 <— 题目传送门点这里 题目描述 战争时期,前线有 nnn 个哨所,每个哨所可能会与其他若干个哨所之间有通信联系。 信使负责在哨所之间传递信息,当然,…...

Paddle OCR Win 11下的安装和简单使用教程
Paddle OCR Win 11下的安装和简单使用教程 对于中文的识别,可以考虑直接使用Paddle OCR,识别准确率和部署都相对比较方便。 环境搭建 目前PaddlePaddle 发布到v2.4,先下载paddlepaddle,再下载paddleocr。根据自己设备操作系统进…...

杂谈:数组index问题和对象key问题
面试题一: var arr [1, 2, 3, 4] 问:arr[1] ?; arr[1] ?答:arr[1] 2; arr[1] 2 这里可以再分为两个问题: 1、数组赋值 var arr [1, 2, 3, 4]arr[1] 10; // 数字场景 arr[10] 1; // 字符串场景 arr[a] 1; // 字符串…...
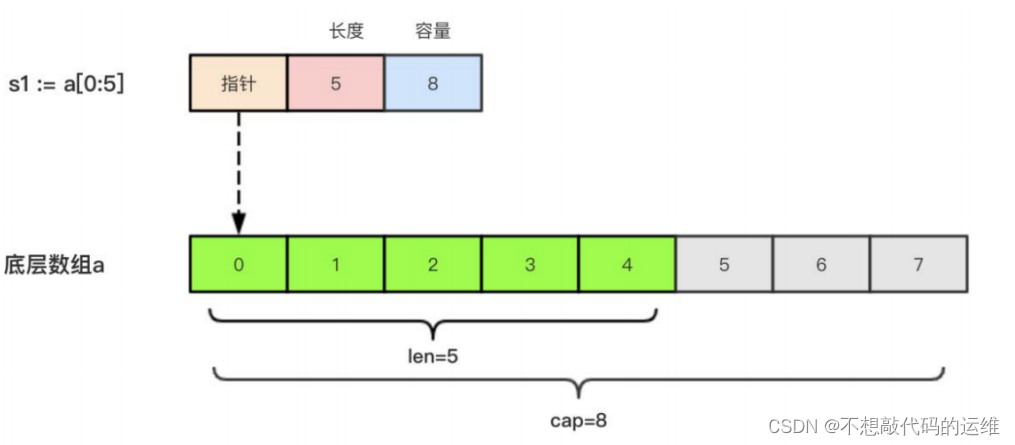
三天Golang快速入门—Slice切片
三天Golang快速入门—Slice切片Slice切片切片原理切片遍历append函数操作切片append添加append追加多个切片中删除元素切片合并string和slice的联系Slice切片 切片原理 由三个部分构成,指针、长度、容量指针:指向slice第一个元素对应的数组元素的地址长…...
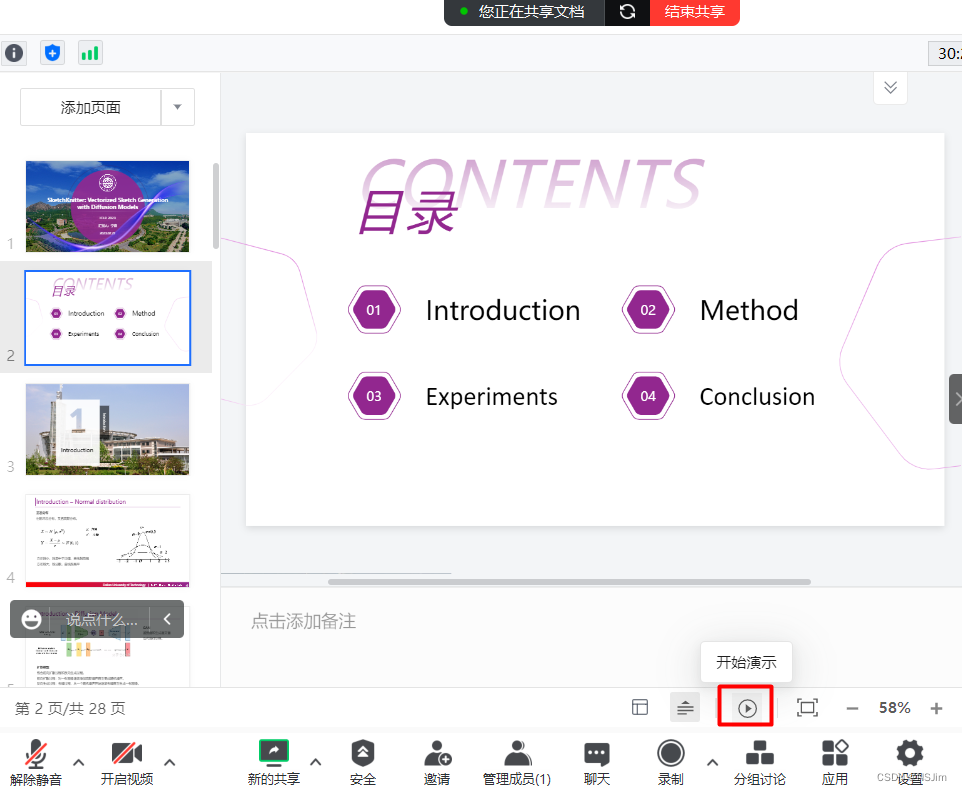
腾讯会议演示者视图/演讲者视图
前言 使用腾讯会议共享PPT时,腾讯会议支持共享用户使用演示者视图/演讲者视图,而会议其他成员可以看到正常的放映视图。下面以Win10系统和Office为例,介绍使用步骤。值得一提的是,该方法同时适用于单显示屏和多显示屏。 腾讯会议…...
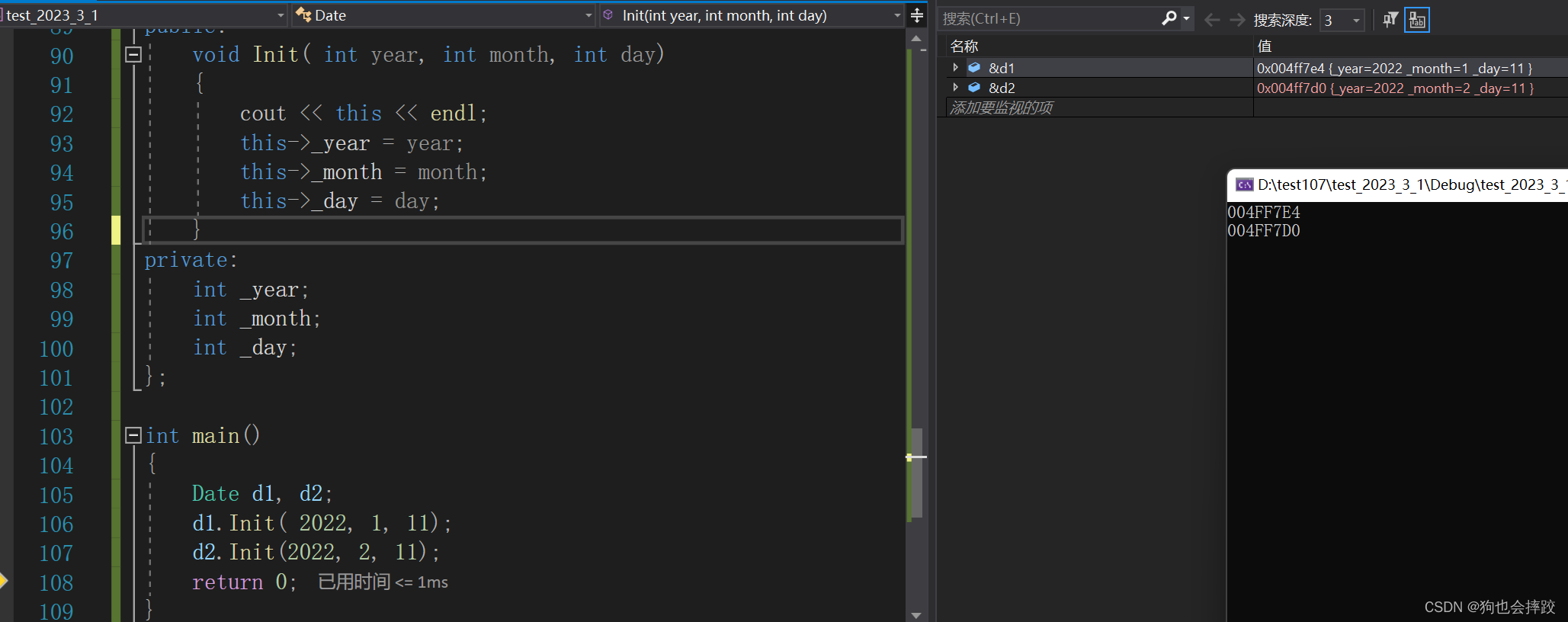
【C++】类与对象(一)
文章目录1、面向过程和面向对象初步认识2、类的引入3、类的定义4、类的访问限定符5、类的作用域6、类的实例化7、计算类对象的大小8、this指针9、 C语言和C实现Stack的对比1、面向过程和面向对象初步认识 C语言是面向过程的,关注的是过程,分析出求解问题…...

JavaScript基本语法
本文提到的绝大多数语法都是与Java不同的语法,相同的就不会赘述了.JavaScript的三种引入方式内部js<body><script>alert(hello);</script> </body>行内js<body><div onclick"alert(hello)">这是一个div 点击一下试试</div>…...

OpenCV4.x图像处理实例-道路车辆检测(基于背景消减法)
通过背景消减进行道路车辆检测 文章目录 通过背景消减进行道路车辆检测1、车辆检测思路介绍2、BackgroundSubtractorMOG23、车辆检测实现在本文中,将介绍如何使用简单但有效的背景-前景减法方法执行车辆检测等任务。本文将使用 OpenCV 中使用背景-前景减法和轮廓检测,以及如何…...
pwnlab通关流程
pwnlab通关 关于文件包含,环境变量劫持的一个靶场 信息收集 靶机ip:192.168.112.133 开放端口 根据开放的端口信息决定从80web端口入手 目录信息 在images和upload路径存在目录遍历,config.php被渲染无法查看,upload.php需…...

面向过程与面向对象的区别与联系
目录 什么是面向过程 什么是面向对象 区别 各自的优缺点 什么是面向过程 面向过程是一种以事件为中心的编程思想,编程的时候把解决问题的步骤分析出来,然后用函数把这些步骤实现,在一步一步的具体步骤中再按顺序调用函数。 什么是面向对…...
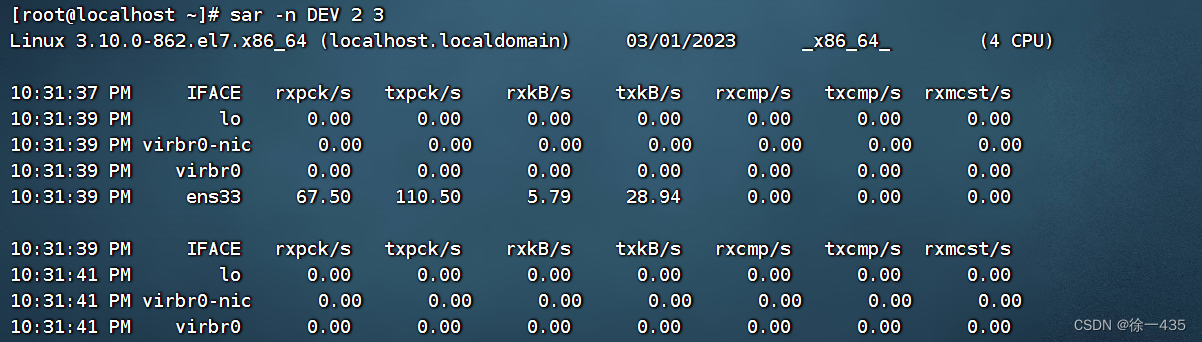
主机状态(查看资源占用情况、查看网络占用情况)
1. 查看资源占用情况 【1】可以通过top命令查看cpu、内存的使用情况,类似windows的任务管理器 默认5s刷新一次 语法:top 可 Ctrl c 退出 2.磁盘信息监控 【1】使用df命令,查看磁盘信息占用情况 语法:df [ -h ] 以更加人性化…...
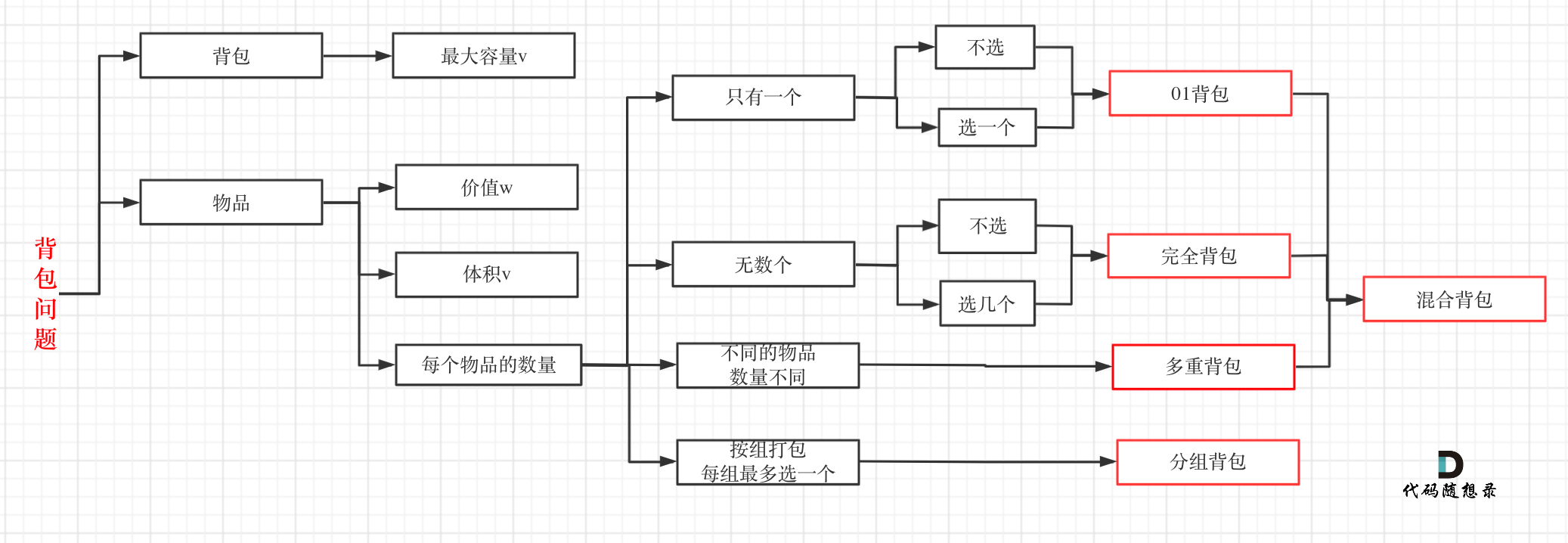
代码随想录算法训练营第四十一天 | 01背包问题-二维数组滚动数组,416. 分割等和子集
一、参考资料01背包问题 二维 https://programmercarl.com/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.html 视频讲解:https://www.bilibili.com/video/BV1cg411g7Y6 01背包问题 一维 https://programmercarl.com/%E8%83%8C%E5…...

VMware NSX 4.1 发布 - 网络安全虚拟化平台
请访问原文链接:VMware NSX 4 - 网络安全虚拟化平台,查看最新版。原创作品,转载请保留出处。 作者主页:www.sysin.org VMware NSX 提供了一个敏捷式软件定义基础架构,用来构建云原生应用程序环境。NSX 专注于为具有异…...

计算理论 复杂度预备知识
文章目录计算理论 复杂度预备知识符号递归表达式求解通项公式主方法Akra-Bazzi 定理计算理论 复杂度预备知识 符号 f(n)o(g(n))f(n)o(g(n))f(n)o(g(n)) :∃c\exists c∃c ,当 nnn 足够大时, f(n)<cg(n)f(n)\lt cg(n)f(n)<cg(n) &#…...
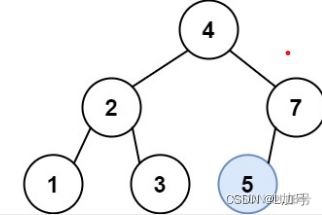
二叉树——二叉搜索树中的插入操作
二叉搜索树中的插入操作 链接 给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。 注意,…...

C# if break,if continue,if return的区别和使用
故事部分: 现在你肚子饿了,想要去: 1.吃个三菜一汤。 2.吃个蛋糕。 3.喝个奶茶。 结果,你吃饭的时候,吃到一个虫子。 你会有几种做法? 1.把有虫子这道菜拿走,继续吃下一道菜 。 2.算了ÿ…...

力扣-第二高的薪水
大家好,我是空空star,本篇带大家了解一道中等的力扣sql练习题。 文章目录前言一、题目:176. 第二高的薪水二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他总结…...
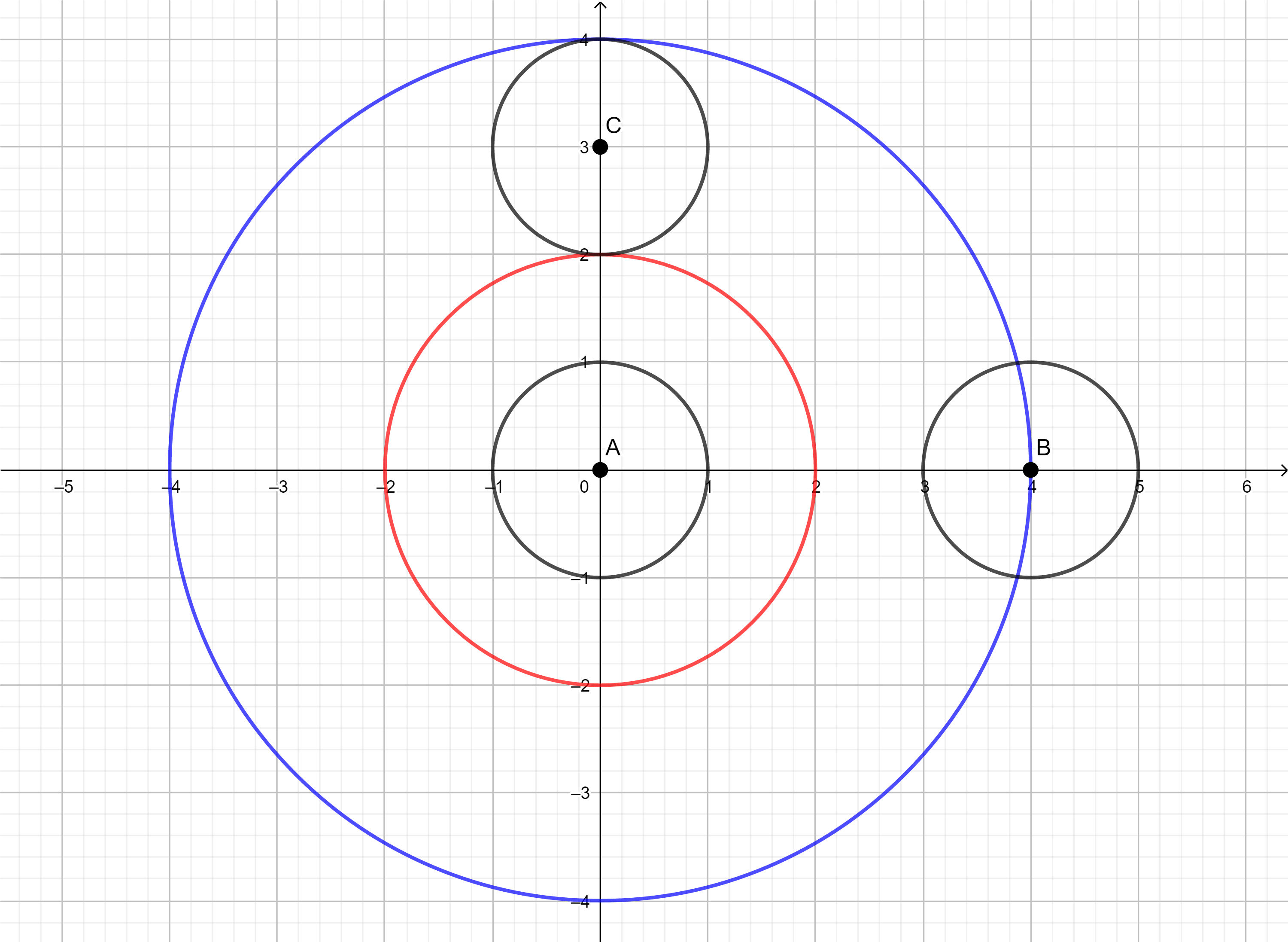
I - 太阳轰炸(组合数学Cnk n固定)
2023河南省赛组队训练赛(二) - Virtual Judge (vjudge.net) 背景:阿塔尼斯,达拉姆的大主教,在艾尔又一次沦陷之后指挥着星灵的最后一艘方舟舰:亚顿之矛。作为艾尔星灵数千年来的智慧结晶,亚顿之…...
centos安装gitlab
更新系统 sudo yum -y update安装所需要的包 sudo yum -y install epel-release curl vim policycoreutils-python如果要安装并使用本地Postfix服务器发送通知,请安装Postfix,这里就不安装了: sudo yum -y install postfix安装后启动并启用…...
)
【洛谷 P1093】[NOIP2007 普及组] 奖学金 题解(结构体排序)
[NOIP2007 普及组] 奖学金 题目描述 某小学最近得到了一笔赞助,打算拿出其中一部分为学习成绩优秀的前 555 名学生发奖学金。期末,每个学生都有 333 门课的成绩:语文、数学、英语。先按总分从高到低排序,如果两个同学总分相同,再…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...

RabbitMQ 各类交换机
为什么要用交换机? 交换机用来路由消息。如果直发队列,这个消息就被处理消失了,那别的队列也需要这个消息怎么办?那就要用到交换机 交换机类型 1,fanout:广播 特点 广播所有消息:将消息…...

Cursor AI 账号纯净度维护与高效注册指南
Cursor AI 账号纯净度维护与高效注册指南:解决限制问题的实战方案 风车无限免费邮箱系统网页端使用说明|快速获取邮箱|cursor|windsurf|augment 问题背景 在成功解决 Cursor 环境配置问题后,许多开发者仍面临账号纯净度不足导致的限制问题。无论使用 16…...
