连锁零售企业如何提高异地组网的稳定性?
随着数字化时代的到来,连锁零售企业面临着日益复杂和多样化的网络挑战。连锁零售企业是在不同地理位置拥有分支机构和零售店,可能同城或异地,需要确保各个地点之间的网络连接稳定和可靠。但由于不同地区的网络基础设施差异、网络延迟和带宽限制等因素,实现异地组网稳定性变成具有挑战性的任务。而且还面临大容量的数据传输和实时的数据处理需求,这对网络带宽和处理能力提出了更高的要求。
以往的企业组网一般是基于专用线路或MPLS(多协议标签交换)网络,可以提供较高的稳定性和可靠性。但是这种方式的部署周期长、维护成本较高,并且不够灵活,也不利于后期扩展。或者自己搭建VPN,但这种方式需要专业的技术人员来实现,而且网络质量受限于公共互联网、安全性相对较低,可能存在带宽限制。
为解决连锁零售企业面临的复杂网络挑战,确保异地组网的稳定性,需要选择更合适的网络连接方式,比如采用SD-WAN实现,SD-WAN是一种灵活、安全且可靠的企业组网解决方案。

SD-WAN技术优势:
-
SD-WAN智能路由功能,根据实时的网络条件选择最佳路径来传输数据流量
这对于连锁零售企业来说尤为重要,这意味着即使在不同分支机构或零售店之间存在多个网络连接供应商,SD-WAN能够实现自动切换和负载均衡,确保数据传输的稳定性和可靠性,保证分支机构之间的信息共享和协作的畅通无阻。
-
提供强大的网络安全功能,帮助应对日益增长的网络威胁
SD-WAN可以通过加密和身份验证等方式,确保数据的安全传输。支持集中式的网络安全策略管理,助力连锁零售企业能够更好地监控和保护整个网络,减少潜在的安全漏洞和威胁。
-
SD-WAN的灵活性和可扩展性更好地支持连锁零售企业不断变化的网络需求
SD-WAN可以根据实际需要进行快速部署和配置,无论是新增分支机构或店铺还是调整网络拓扑,都可以简化且高效地实现。如果企业业务上云,SD-WAN可以和云服务无缝集成,连锁零售企业能最快使用云服务、SaaS应用等。
SD-WAN作为综合性的网络解决方案,能够有效应对连锁零售企业组网面临的复杂和多样化的网络挑战,提供所需的稳定、高效和安全的异地组网解决方案。
相关文章:

连锁零售企业如何提高异地组网的稳定性?
随着数字化时代的到来,连锁零售企业面临着日益复杂和多样化的网络挑战。连锁零售企业是在不同地理位置拥有分支机构和零售店,可能同城或异地,需要确保各个地点之间的网络连接稳定和可靠。但由于不同地区的网络基础设施差异、网络延迟和带宽限…...

如何靠掌握自己的大数据打破信息流的壁垒?
在当今数字化时代,打造自己的私域流量已经成为商家乃至获取竞争优势的关键手段之一。通过掌握自己的大数据,可以更好地了解用户需求和市场趋势,优化产品和服务,从而打破信息流的壁垒。本文将就如何通过打造自己的私域流量并掌握大…...
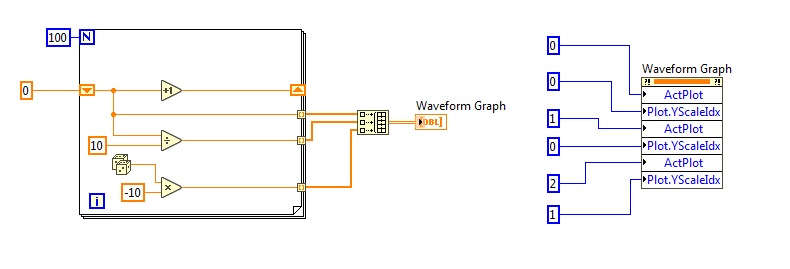
LabVIEW绘制带有多个不同标尺的波形图
LabVIEW绘制带有多个不同标尺的波形图 通过在同一波形图上使用多个轴,可以使用不同的标尺绘制数据。请按照以下步骤操作。 将波形图或图表控件放在前面板上。 1. 右键点击您要创建多个标尺的轴,然后选择复制标尺。例如,如果要为一个…...

Oracle行转列,列转行使用实例
-----1.行转换为列 select a.fworkcenter as 车间,F1||-数量 as 类型, fspec as 规格 ,ftype as 前缀 , to_char(fdate,YYYY-MM-dd) as 日期, (case when a.fcode in (900,901) then to_char(fcount,fm90.990) else cast(fcount as varchar(20)) end) 值 , …...

056-第三代软件开发-软件打包
第三代软件开发-软件打包 文章目录 第三代软件开发-软件打包项目介绍软件打包1 下载 linuxdepoyqt 工具2 安装 linuxdepoyqt3 qmake配置4 打包程序 总结 关键字: Qt、 Qml、 linuxdeployqt、 Ubuntu、 AppImage 项目介绍 欢迎来到我们的 QML & C 项目&…...

C++相关闲碎记录(2)
1、误用shared_ptr int* p new int; shared_ptr<int> sp1(p); shared_ptr<int> sp2(p); //error // 通过原始指针两次创建shared_ptr是错误的shared_ptr<int> sp1(new int); shared_ptr<int> sp2(sp1); //ok 如果对C相关闲碎记录(1)中记录的shar…...

如何快速搭建一个大模型?简单的UI实现
🔥博客主页:真的睡不醒 🚀系列专栏:深度学习环境搭建、环境配置问题解决、自然语言处理、语音信号处理、项目开发 💘每日语录:相信自己,一路风景一路歌,人生之美,正在于…...

国家开放大学 平时作业 测试题 训练
试卷代号:1340 古代小说戏曲专题 参考试题(开卷) 一、选择(每题1分,共10分) 1.下列作品中属于唐传奇的是( )。 A.《公孙九娘》 B.《观音作别》 C《碾玉观音》 …...
)
后端防止重复提交相同数据处理方式(Redis)
使用AOP注解处理接口幂等性,默认禁止同一用户在上次提交未果后10秒内又重复提交 在原先的sameUrlData的注解上进行了copy新建优化,使用redis去setnx的参数视项目使用点而调整,不一定是每个项目都适合这种取参形式。 源码如下: package com…...

最小栈[中等]
优质博文:IT-BLOG-CN 一、题目 设计一个支持push,pop,top操作,并能在常数时间内检索到最小元素的栈。 实现MinStack类: MinStack()初始化堆栈对象。 void push(int val)将元素val推入堆栈。 void pop()删除堆栈顶部的元素。 in…...
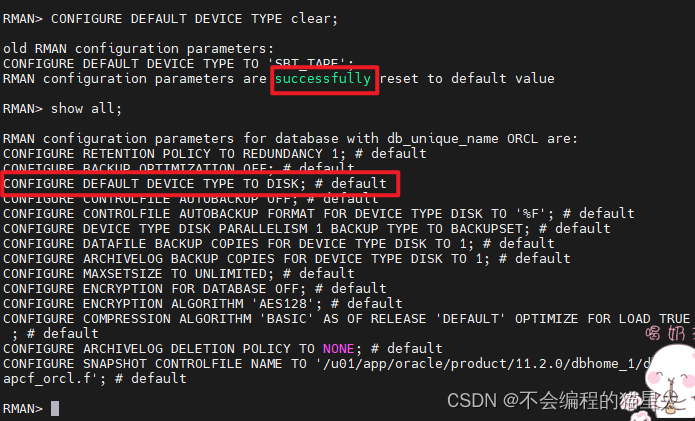
Oracle(2-9) Oracle Recovery Manager Overview and Configuration
文章目录 一、基础知识1、User Backup VS RMAN2、Restoring &Recovering DB 还原&恢复数据库3、Recovery Manager Features 管理恢复功能4、RMAN Components RMAN组件5、Repository1: Control File 存储库1:控制文件6、Channel Allocation 通道道分配7、Media Manageme…...
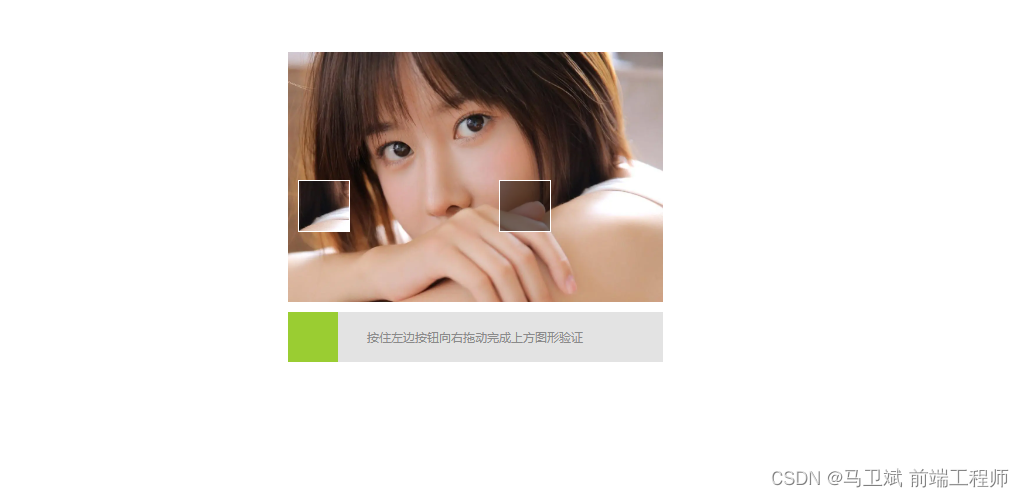
滑动验证码
先上图 代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>滑动验证码</title><style>* {margin: 0;padding: 0;}.box {position: relative;width: 375px;margin: 100px a…...

数据爬取+可视化实战_告白气球_词云展示----酷狗音乐
一、前言 歌词上做文本分析,数据存储在网页上,需要爬取数据下来,词云展示在工作中也变得日益重要,接下来将数据爬虫与可视化结合起来,做个词云展示案例。 二、代码 # -*- coding:utf-8 -*- # 酷狗音乐 通过获取每首歌…...

rkmedia_vi_get_frame_test.c 代码解析
使用示例: 录像: rkmedia_vi_get_frame_test -a /etc/iqfiles/ -I 1 -o 1080.nv12 然后用yuvplayer.exe可以播放。 录像10帧: rkmedia_vi_get_frame_test -a /etc/iqfiles/ -I 1 -o 1080.nv12 -c 10 解析代码: #include <as…...

探究Kafka原理-3.生产者消费者API原理解析
👏作者简介:大家好,我是爱吃芝士的土豆倪,24届校招生Java选手,很高兴认识大家📕系列专栏:Spring源码、JUC源码、Kafka原理🔥如果感觉博主的文章还不错的话,请ὄ…...

Linux系统iptables扩展
目录 一. iptables规则保存 1. 导出规则保存 2. 自动重载规则 ①. 当前用户生效 ②. 全局生效 二. 自定义链 1. 新建自定义链 2. 重命名自定义链 3. 添加自定义链规则 4. 调用自定义链规则 5. 删除自定义链 三. NAT 1. SNAT 2. DNAT 3. 实验 ①. 实验要求 ②. …...

Openwrt 系统安装 插件名称与中文释义
系统镜像 当时是去官网找对应的,但是作为门外汉,想简单,可以试试这个网站 插件 OpenWrt/Lede全部插件列表功能注释...
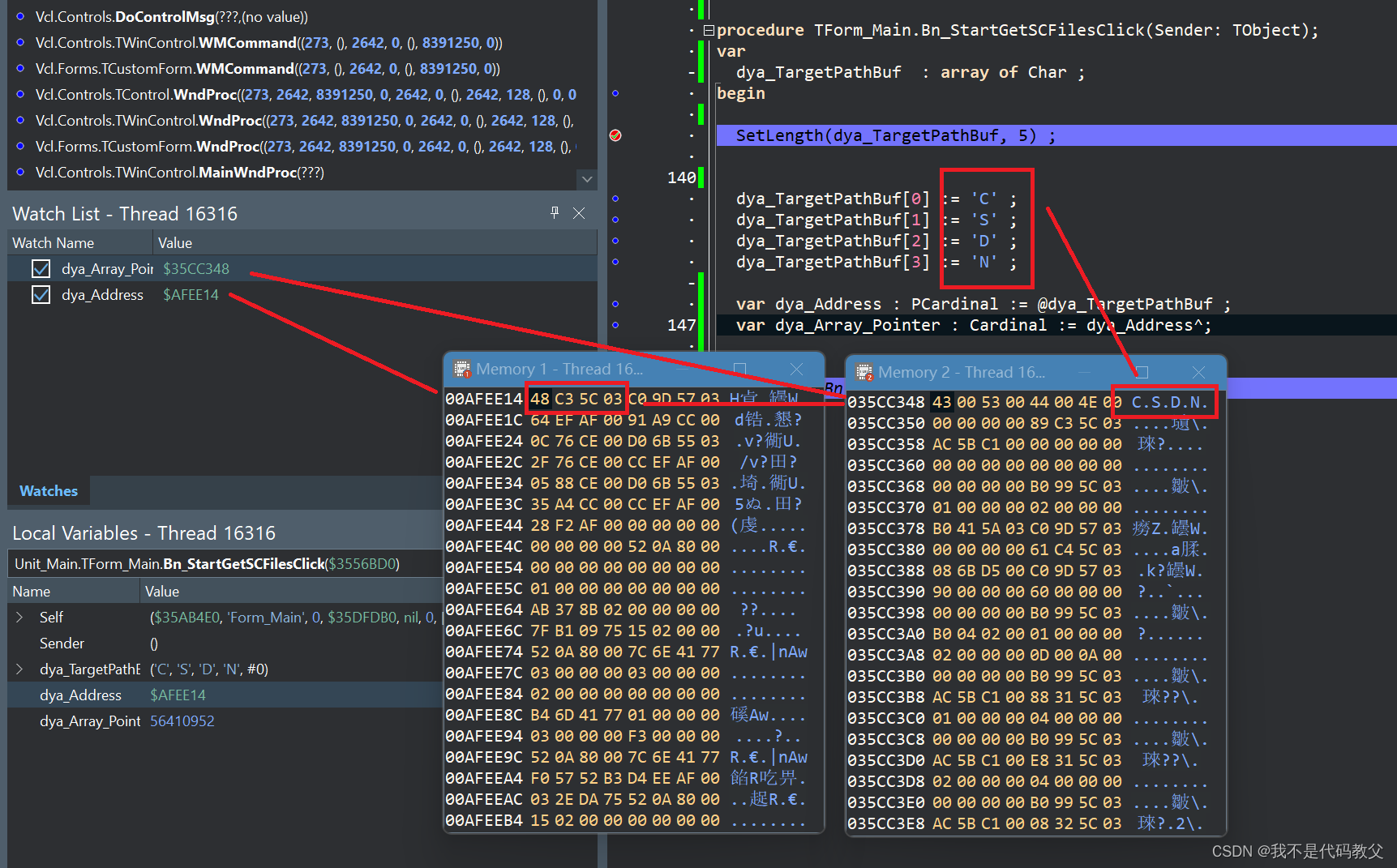
[原创]Delphi的SizeOf(), Length(), 动态数组, 静态数组的关系.
[简介] 常用网名: 猪头三 出生日期: 1981.XX.XXQQ: 643439947 个人网站: 80x86汇编小站 https://www.x86asm.org 编程生涯: 2001年~至今[共22年] 职业生涯: 20年 开发语言: C/C、80x86ASM、PHP、Perl、Objective-C、Object Pascal、C#、Python 开发工具: Visual Studio、Delphi…...
:bind_front)
C++(20):bind_front
C(11):bind_c11 bind_风静如云的博客-CSDN博客 提供了方法来绑定函数参数的方法。 C20提供了bind_front用于简化这个绑定。 #include <iostream> #include <functional> using namespace std;void func1(int d1, int d2) {cout<<__func__<&l…...

【spring】bean的后处理器
目录 一、作用二、常见的bean后处理器2.1 AutowiredAnnotationBeanPostProcessor2.1.1 说明2.1.2 代码示例2.1.3 截图示例 2.2 CommonAnnotationBeanPostProcessor2.2.1 说明2.2.2 代码示例2.2.3 截图示例 2.3 ConfigurationPropertiesBindingPostProcessor2.3.1 说明2.3.2 代码…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
