剑指 Offer 14-剪绳子
摘要
剑指 Offer 14- I. 剪绳子
剑指 Offer 14- II. 剪绳子 II
343. 整数拆分
一、动态规划解析
这道题给定一个大于1的正整数n,要求将n 拆分成至少两个正整数的和,并使这些正整数的乘积最大化,返回最大乘积。令x是拆分出的第一个正整数,则剩下的部分是 n−x,n−x可以不继续拆分,或者继续拆分成至少两个正整数的和。由于每个正整数对应的最大乘积取决于比它小的正整数对应的最大乘积,因此可以使用动态规划求解。
创建数组dp,其中dp[i]表示将正整数i拆分成至少两个正整数的和之后,这些正整数的最大乘积。特别地,0不是正整数,1是最小的正整数,0和1都不能拆分,因此 dp[0]=dp[1]=0。
当 i≥2时,假设对正整数i拆分出的第一个正整数是 j(1≤j<i),则有以下两种方案:
- 将i拆分成j 和i−j的和,且i−j不再拆分成多个正整数,此时的乘积是j×(i−j);
- 将i拆分成j和i−j的和,且i−j继续拆分成多个正整数,此时的乘积是j×dp[i−j]。
因此,当j固定时,有 dp[i]=max(j×(i−j),j×dp[i−j])。由于j的取值范围是1到i−1,需要遍历所有的j得到dp[i]的最大值,因此可以得到状态转移方程如下:dp[i]=max(1≤j<i){max(j×(i−j),j×dp[i−j])}。最终得到dp[n]的值即为将正整数n拆分成至少两个正整数的和之后,这些正整数的最大乘积。
package DP;/*** @Classname JZ14* @Description TODO* @Date 2023/3/1 21:34* @Created by xjl*/
public class JZ14剪绳子 {public int cuttingRope(int n) {// 定义dp的数组 dp[0]=dp[1]=0int[] dp = new int[n + 1];for (int i = 2; i <= n; i++) {int curMax = 0;for (int j = 1; j < i; j++) {curMax = Math.max(curMax, Math.max(j * (i - j), j * dp[i - j]));}dp[i] = curMax;}return dp[n];}
}
复杂度分析
- 时间复杂度:O(n^2),其中n是给定的正整数。对于从2到n的每一个整数都要计算对应的dp 值,计算一个整数对应的 dp值需要O(n)的时间复杂度,因此总时间复杂度是O(n^2)。
- 空间复杂度:O(n),其中n是给定的正整数。创建一个数组dp,其长度为 n+1
二、数学方法实现
设将长度为n的绳子切为a段:n=n1+n2+...+na,题等价于求解:max(n1×n2×...×na),以下公式为“算术几何均值不等式” ,等号当且仅当n1=n2=...=na时成立。
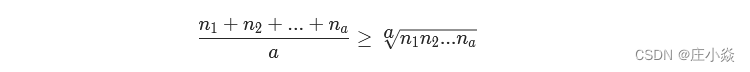

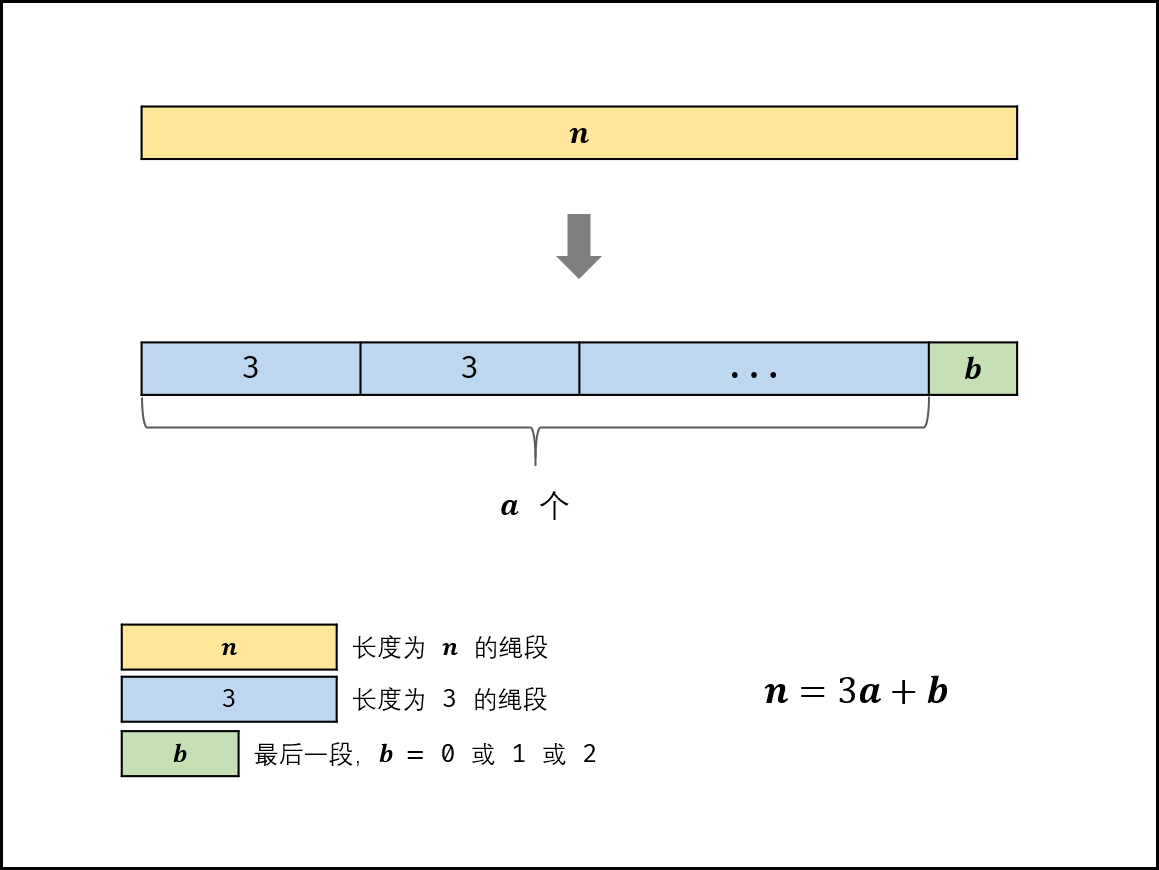
算法流程:
- 当n≤3时,按照规则应不切分,但由于题目要求必须剪成m>1段,因此必须剪出一段长度为1的绳子,即返回 n−1。
- 当n>3时,求n除以3的 整数部分a和余数部分b (即n=3a+b),并分为以下三种情况:
- 当 b=0时,直接返回3a;
- 当 b=1时,要将一个 1+3转换为 2+2,因此返回 3a−1×4;
- 当 b=2时,返回 3a×2。
class Solution {public int cuttingRope(int n) {if(n <= 3) return n - 1;int a = n / 3, b = n % 3;if(b == 0) return (int)Math.pow(3, a);if(b == 1) return (int)Math.pow(3, a - 1) * 4;return (int)Math.pow(3, a) * 2;}
}三、大数越界情况下的求余问题
此题与剪绳子主体等价,唯一不同在于本题目涉及 “大数越界情况下的求余问题” 。

切分规则:
- 最优:3。把绳子尽可能切为多个长度为3的片段,最后一段绳子长度可能为0,1,2三种情况。
- 次优:2。若最后一段绳子长度为2 ;则保留,不再拆为 1+1 。
- 最差:1。若最后一段绳子长度为1 ;则应把一份3+1替换为 2+2,因为 2×2>3×1。
算法流程:
当n≤3时,按照规则应不切分,但由于题目要求必须剪成m>1段,因此必须剪出一段长度为1的绳子,即返回n−1。
当n>3时,求n除以 3的整数部分a和余数部分b (即 n=3a+b ),并分为以下三种情况(设求余操作符号为 "⊙" ):
- 当 b=0时,直接返回 3a⊙1000000007;
- 当 b=1时,要将一个 1+3转换为 2+2,因此返回 (3a−1×4)⊙1000000007;
- 当 b=2时,返回 (3a×2)⊙1000000007。
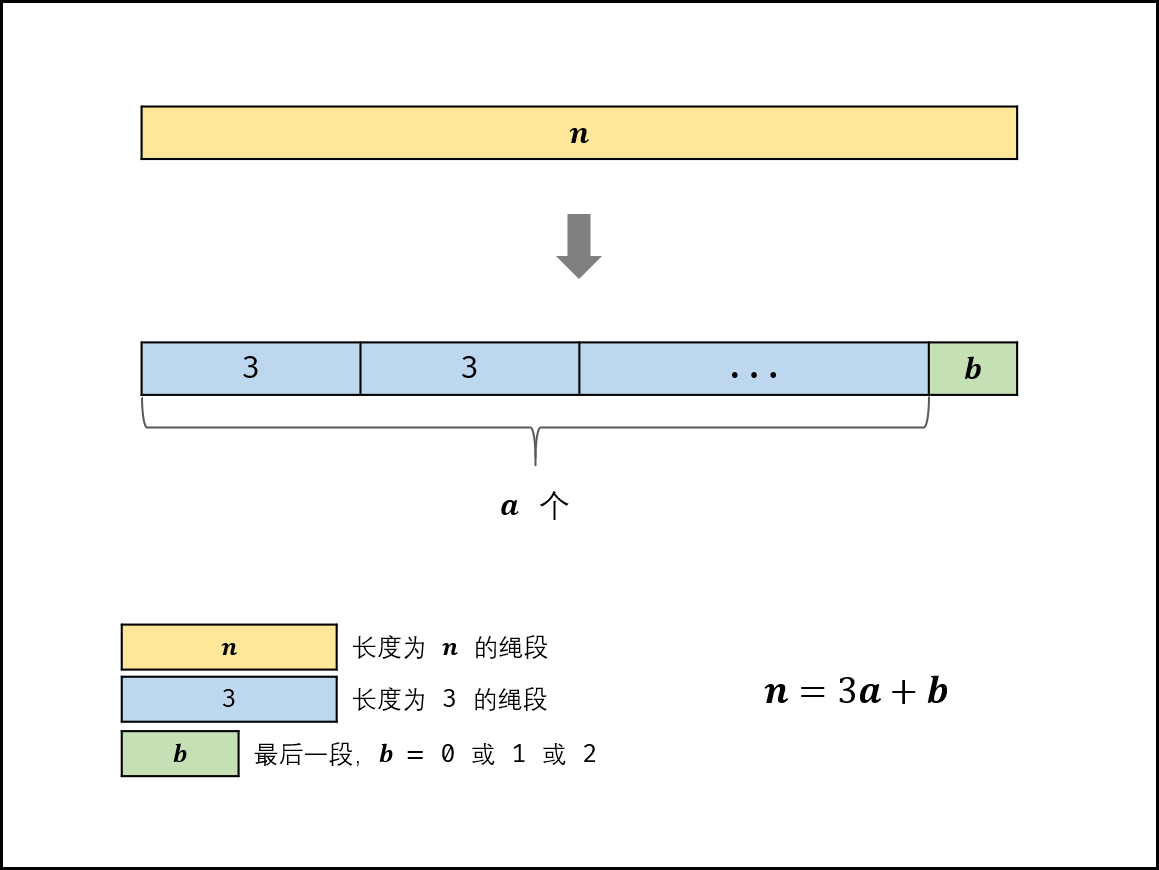
大数求余解法:
- 大数越界:当a增大时,最后返回的3a大小以指数级别增长,可能超出int32 甚至int64 的取值范围,导致返回值错误。
- 大数求余问题: 在仅使用int32 类型存储的前提下,正确计算xa对p求余(即 xa⊙p)的值。
- 解决方案: 循环求余、快速幂求余 ,其中后者的时间复杂度更低,两种方法均基于以下求余运算规则推出:(xy)⊙p=[(x⊙p)(y⊙p)]⊙p
class Solution {public int cuttingRope(int n) {if(n <= 3) return n - 1;int b = n % 3, p = 1000000007;long rem = 1, x = 3;for(int a = n / 3 - 1; a > 0; a /= 2) {if(a % 2 == 1) rem = (rem * x) % p;x = (x * x) % p;}if(b == 0) return (int)(rem * 3 % p);if(b == 1) return (int)(rem * 4 % p);return (int)(rem * 6 % p);}
}博文参考
《leetcode》
相关文章:

剑指 Offer 14-剪绳子
摘要 剑指 Offer 14- I. 剪绳子 剑指 Offer 14- II. 剪绳子 II 343. 整数拆分 一、动态规划解析 这道题给定一个大于1的正整数n,要求将n 拆分成至少两个正整数的和,并使这些正整数的乘积最大化,返回最大乘积。令x是拆分出的第…...
泰克示波器|MSO64示波器的应用
泰克新一代示波器MSO64为实例来讲解时频域信号分析技术。MSO64采用全新TEK049平台,不仅实现了4通道同时打开时25GS/s的高采样率,而且实现了12-bit高垂直分辨率。同时,由于采用了新型低噪声前端放大ASIC—TEK061,大大降低了噪声水平…...
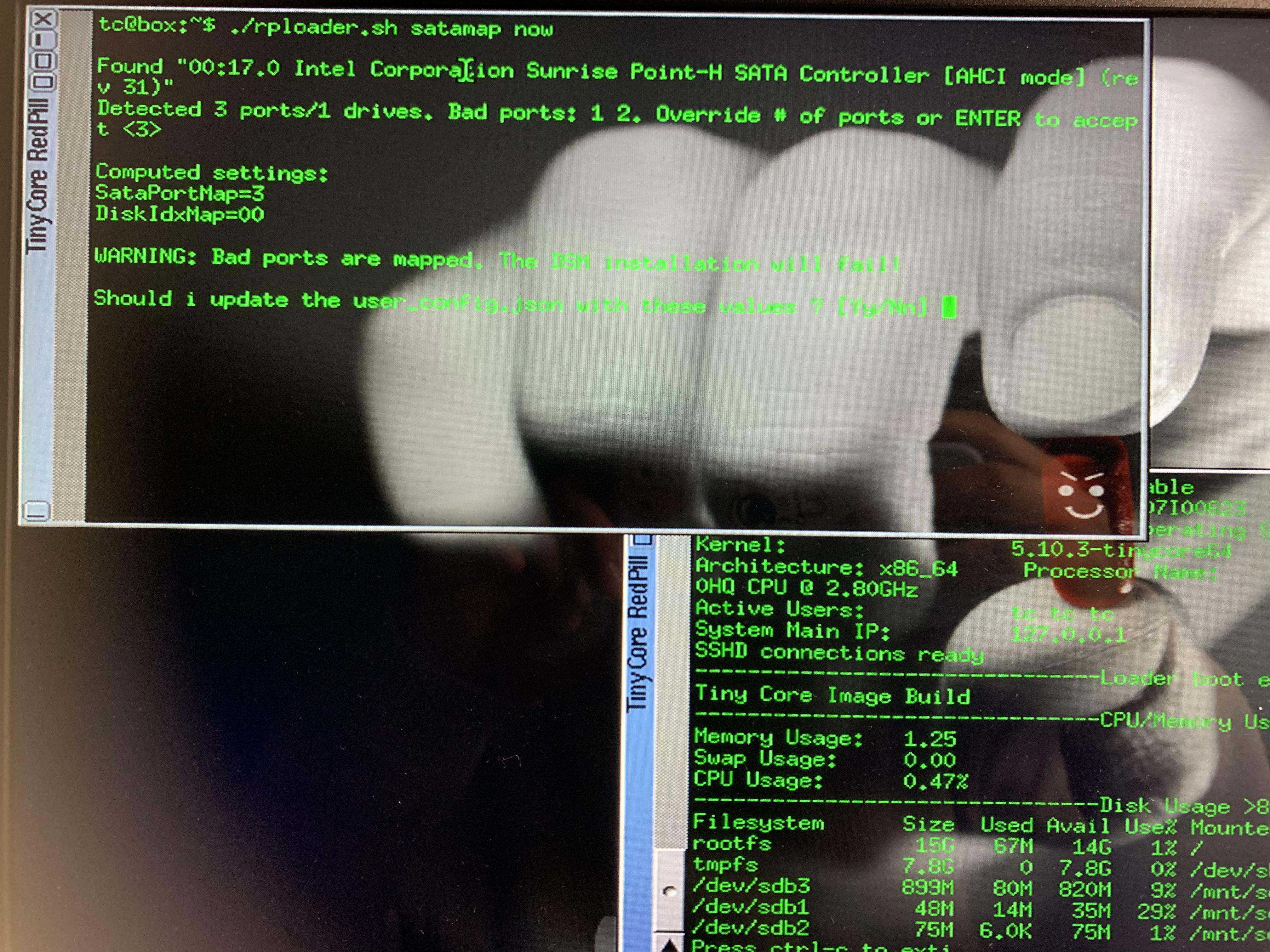
1.4 黑群晖安装:SataPortMap和DiskIdxMap两种获取方式
tinycore及安装工具下载:工具:链接:https://pan.baidu.com/s/1CMLl6waOuW-Ys2gKZx7Jgg?pwdchct提取码:chcttinycore:链接:https://pan.baidu.com/s/19lchzLj-WDXPQu2cEcskBg?pwddcw2 提取码:d…...
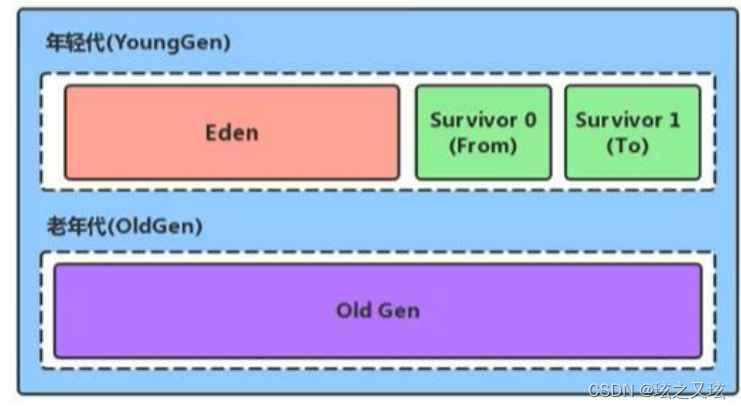
JVM虚拟机概述(2)
3.JVM 运行时数据区 3.1.1 程序计数器(Program Counter Register) 是一块很小的内存空间,用来记录每个线程运行的指令位置,是线程私有的,每个线程都拥有一个程序计数器,生命周期与线程一致,是运行时数据区中唯一一个不…...

Intel CSME 简述
SME 算是 Intel X86 PC 上最神秘的部分了,本文根据 us-19-Hasarfaty-Behind-The-Scenes-Of-Intel-Security-And-Manageability-Engine 一文写成。讲述内容无法证伪,各位随便听听即可,了解这些能够帮助BIOS 工程师更好的理解一些操作的实现。文章基于 Intel 第八代第九代CPU(…...

复位理论基础
先收集资料,了解当前常用的基础理论和实现方式 复位 初始化微控制器内部电路 将所有寄存器恢复成默认值确认MCU的工作模式禁止全局中断关闭外设将IO设置为高阻输入状态等待时钟趋于稳定从固定地址取得复位向量并开始执行 造成复位的原因 有多种引起复位的因素&…...
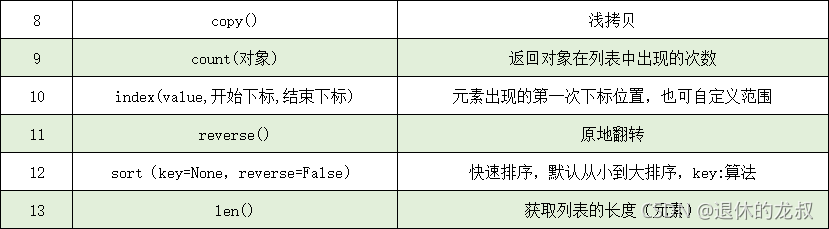
Python基础知识——列表
列表 列表是可以存放任何数据,包括整型,浮点型,字符串,布尔型等等,是常用的数据类型之一。 1.列表的创建 列表也是一个可迭代对象 1. 普通形式l [1,2,3,4,5] ---整型列表l ["a","b","c&…...

如何使用工时表管理项目和非项目的资源?
对新机会做出反应的能力是企业竞争优势的关键。项目不断涌现,企业需要了解具体的可用性以及是否有资源来接受新事物。更进一步来说,企业需要知道员工将时间花在哪里。 使用 8Manage工时表解决方案,你将始终拥有做出正确业务决策所需的全面知…...

项目经理如何做好质量保证与标准维持?非技术项目经理如何做好质量管控?
项目经理如何做好质量保证与标准维持?非技术项目经理如何做好质量管控?01.质量保障需要重视哪些执行层面的细节02.非技术出身项目经理如何做好质量保障工作03.质量管理除了PDCA,还有哪些推荐的方法04.质量保证与标准维持,作为常态…...

[文件操作] File 类的用法和 InputStream, OutputStream 的用法
能吃是不是件幸福的事呢 文章目录前言1. 文件的相关定义2. 文件类型3. Java对文件系统的操作3.1 对文件的基础操作3.2 读文件3.3 写文件前言 从这章开始,我们就开始学文件操作相关的知识了~ 1. 文件的相关定义 1.文件的定义可以从狭义和广义两个方面解释. 狭义: 指硬盘上的文…...
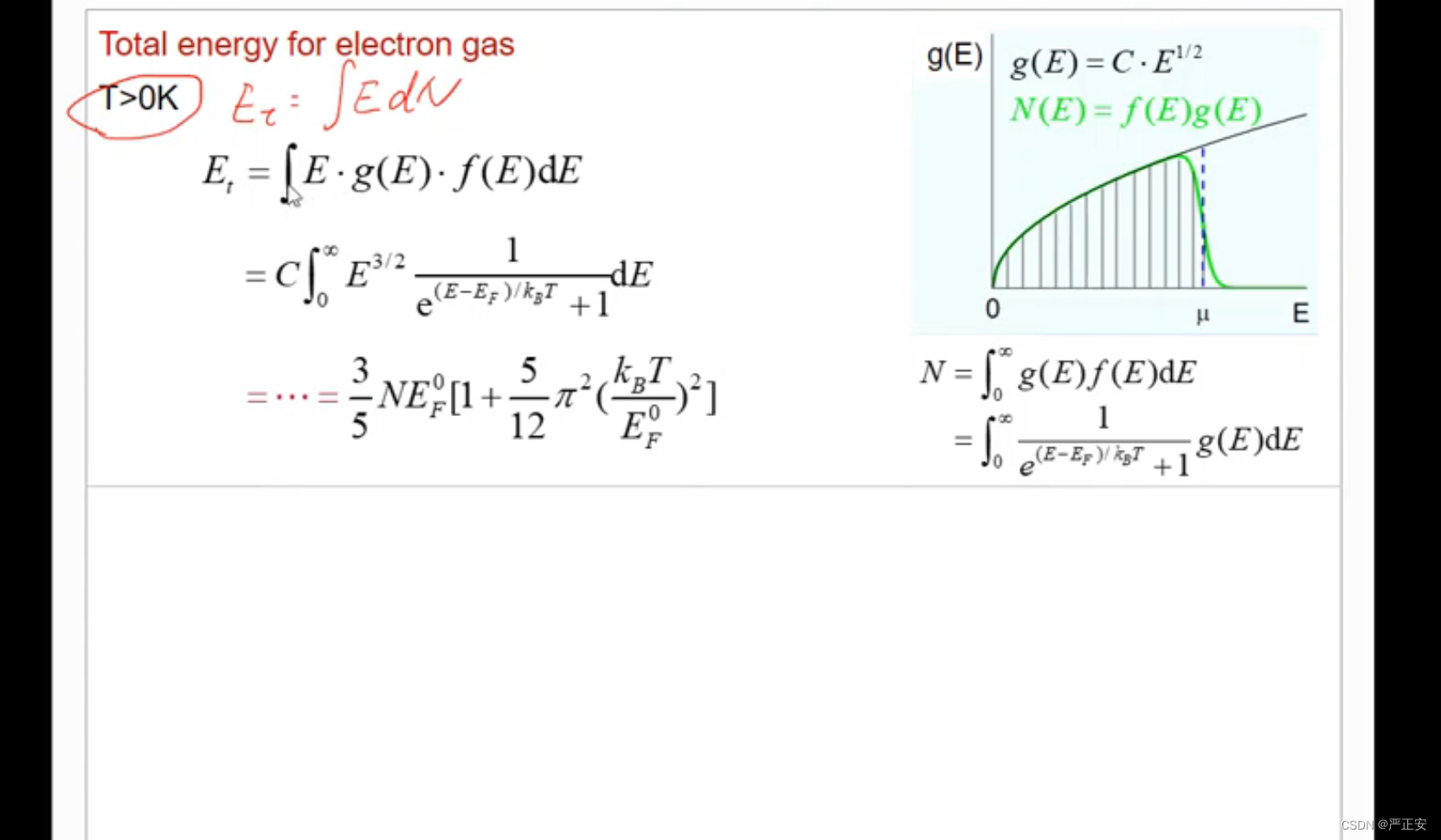
索莫菲模型的一些理解 Smomerfeld Model
如何解释传统热容算出来的数值与量子模型下的区别? 因为只有费米能附近的电子才能够进行移动,这个是问题的差别所在 我们下面就来介绍如何求费米能(费米能的计算) 既然费米能附近的电子很重要,那么附近的电子有多少很…...
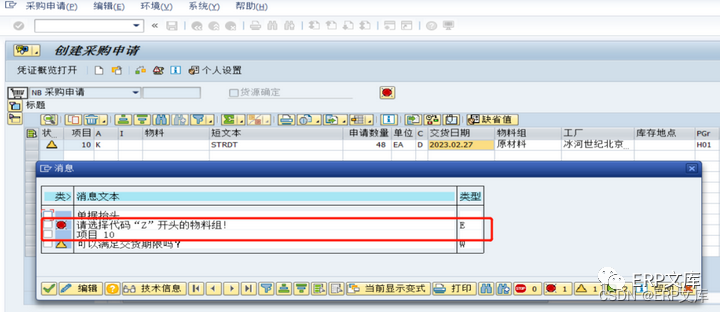
SAP ERP系统MM模块常用增强之四:采购申请输入字段的校验检查
在SAP/ERP项目的实施中采购管理模块(MM)的创建和修改采购申请一般都会有输入字段校验检查的需求,来防止业务人员录入错误或少录入数据,这方面需求部分是可以通过配置实现,比如一些字段是否必输,是否显示等&…...
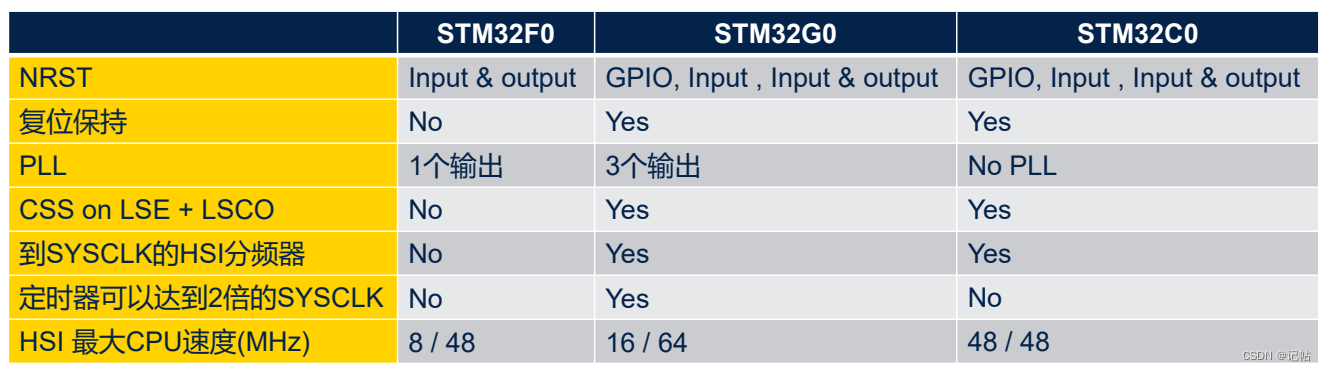
STM32C0介绍(1)----概述
概述 STM32C0系列微控制器是意法半导体公司推出的一款低功耗、高性能的微控制器产品。它们被设计用于需要小型、低功耗和高度可集成的应用程序,如传感器、消费品、电池供电设备、家庭自动化和安全等应用。该系列的微控制器采用ARM Cortex-M0内核,具有丰…...
引导程序开发之一)
windows无盘启动技术开发之传统BIOS(Legacy BIOS)引导程序开发之一
by fanxiushu 2023-03-01 转载或引用请注明原始作者。这个话题可能有点老,UEFI BIOS 已经大量存在,而Legacy BIOS最终会被取代。但是也是作为无盘启动技术里不可或缺的,毕竟还有许多老型号的电脑存在,而且为了兼容性,有…...

mysql实现if语句判断功能的六种使用形式
文章目录 前言一、ifnull函数二、nullif函数三、if函数四、if语句(多用于存储过程)五、if-else语句(多用于存储过程)六、if-elseif-else语句(多用于存储过程)总结前言 在Mysql数据库中实现判断功能有很多方式,具体又分为函数和if语句形式,函数的好处是可以作为sql的一…...

在Vue3这样子写页面更快更高效
前言 在开发管理后台过程中,一定会遇到不少了增删改查页面,而这些页面的逻辑大多都是相同的,如获取列表数据,分页,筛选功能这些基本功能。而不同的是呈现出来的数据项。还有一些操作按钮。 对于刚开始只有 1ÿ…...

做软件测试,如何才能实现月入20K?
听我的,测试想要月入20k。 首先你要去大厂,不在大厂起码也得在一线城市,北上广深。 二线城市的话成都、杭州最好。 不然的话想都不要想。 像我之前整理过成都的公司,除了字节跳动、蚂蚁金服、滴滴、美团、京东、平安、字节跳动…...
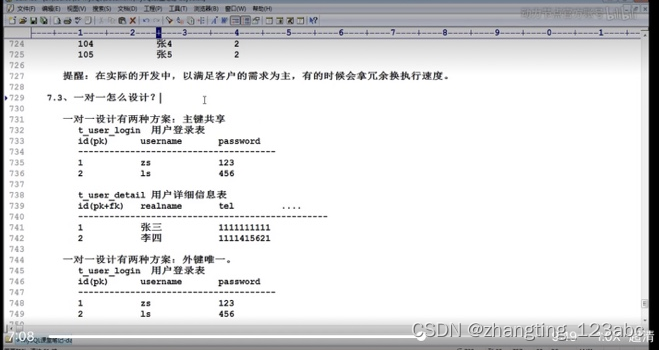
mysql last lesson
1:创建用户 create user zhang identified by 12345678;2:给用户授权,撤销授权, grant.......to revoke ....... 3:将数据库中的数据导出 C:\Windows\system32>mysqldump bjpowernode>C:\bjpowernode.sql -uroot -p12345678 4&#…...

一、Redis入门概述(是什么,能干嘛,去哪下,怎么玩)
一. redis是什么? Redis:REmote Dictionary Server(远程字典服务器)官方解释: Remote Dictionary Server(远程字典服务)是完全开源的,使用ANSIC语言编写遵守BSD协议,是一个高性能的Key-Value数据库提供了丰富的数据结构ÿ…...
当我们在SQL里进行分组的时候,如何才能使用索引?)
(六十二)当我们在SQL里进行分组的时候,如何才能使用索引?
今天我们接着上次的内容来谈谈在SQL语句里假设你要是用到了group by分组语句的话是否可以用上索引,因为大家都知道,有时候我们会想要做一个group by把数据分组接着用count sum之类的聚合函数做一个聚合统计。 那假设你要是走一个类似select count(*) fr…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...
