【算法】动态规划中的路径问题

即使走的再远,也勿忘启程时的初心
C/C++ 游戏开发
Hello,米娜桑们,这里是君兮_,如果给算法的难度和复杂度排一个排名,那么动态规划算法一定名列前茅。今天,我们通过由简单到困难的两道题目带大家学会动态规划中的路径问题
- 好了废话不多说,开始我们今天的学习吧!!
动态规划之路径问题
- 一 不同路径
- 1 题目解析
- 2 算法原理
- 状态表示
- 状态转移方程
- 初始化
- 辅助节点初始化法
- 填表顺序:
- 返回值
- 3 编写代码
- 二 下降路径最小和
- 1 题目解析
- 2 算法原理
- 状态表示
- 状态转移方程
- 初始化
- 填表顺序
- 返回值
- 3 编写代码
- 总结
一 不同路径
- 原题目leetcode链接在这哦 不同路径

1 题目解析
- 如题目所示,在左上角有一个机器人,现在我们需要算出从当前位置到右下角位置一个有多少种不同的路径。
- 注意:重点在于,我们是不能后退的,也就是说,每次进行移动时,只能朝右或者朝下移动。
题目题意理解相对比较简单,就先说到这里
2 算法原理
- 看到这种每一步都与上面一步有所关系的题目,我们首先想到的就是动态规划算法,我们来按照之前提到的动态算法的大致解题思路来进行一步步的分析
状态表示
- 对于这种「路径类」的问题,我们的状态表⽰⼀般有两种形式:
- i. 从dp[i, j] 位置出发,到某个位置去;
- ii. 从起始位置出发,到达dp [i, j] 位置。
分析一下题意,我们需要到达指定的位置,因此这⾥选择第⼆种定义状态表⽰的⽅式:
dp[i][j] 表⽰:⾛到dp[i, j] 位置处,此时一共有几条不同路径
状态转移方程
- 有了上面的状态表示,我们就需要将dp每个位置的值建立一定的联系,方便我们之后的分析
- 如果dp[i][j] 表⽰到达 [i, j] 位置的⽅法数,那么到达 [i, j] 位置之前的⼀⼩步,有两种情况:
- i. 从dp [i, j] 位置的上⽅( dp[i - 1, j] 的位置)向下⾛⼀步,转移到 dp[i, j] 位置;
- ii. 从 dp[i, j] 位置的左⽅( dp[i, j - 1] 的位置)向右⾛⼀步,转移到 dp[i, j] 位置。
由于我们要求的是有多少种⽅法,结合我们上面对题目的解析,因此我们的状态转移⽅程就可以写出了:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
- 注意:这里还有一个很多初学者容易搞混的地方——很多人认为,你现在算出的是通往dp[i][j]这里不同种方法,那么dp[i][j]这一步不应该再加个1吗?
谨记我们这里算的是方法数,不是步数,因此当然不需要+1!
初始化
- 初始化的主要目的有两个,
- 1.防止发生越界访问
- 2.方便我们从已知的信息推出我们需要的信息
这里教给大家一个做动态规划会经常使用的初始化方法
辅助节点初始化法
可以在dp表最前⾯加上⼀个「辅助结点」,帮助我们初始化。使⽤这种技巧要注意两个点:
-
i. 辅助结点⾥⾯的值要「保证后续填表是正确的」;
-
ii. 「下标的映射关系」。
-
好了,相信到这里大家还是一头雾水,下面我来展开讲讲
-
- 有关辅助节点,如果放在这一题来看的话,请问我们的dp[0][0]怎么算呢?
-
- 因此在本题中,我们需要「添加⼀⾏」,并且「添加⼀列」来避免上述越界情况的发生
-
- 因此就有了第一点,我们的辅助节点中保存的值,必须保证对我们的题目的解答没有影响,比如在这个题需将 dp[0][1] (或者dp[1][0])的位置初始化为1 ,剩下创建的值初始化为0,这样就能保证dp[1][1]位置的初始化

- 因此就有了第一点,我们的辅助节点中保存的值,必须保证对我们的题目的解答没有影响,比如在这个题需将 dp[0][1] (或者dp[1][0])的位置初始化为1 ,剩下创建的值初始化为0,这样就能保证dp[1][1]位置的初始化
-
- 那么为什么从dp[1][1] 开始呢?我们的辅助队列相当于在最上后最右的位置帮我们又创建了一行一列来初始化,此时机器人所处的位置就变为了dp[1][1]了
-
- 有关第二点,我们加了一行一列,下标的初始位就不再是dp[0][0]了,因此我们最后返回的值也不是dp[m-1][n-1]而是dp[m][n].。在这个题中下标的映射没啥太大的影响,具体的细节我们放在下个题再讨论
填表顺序:
- 根据状态转移⽅程和题目分析的推导来看,填表的顺序就是「从上往下」填每⼀⾏,在填写每⼀⾏的时候「从左往右」填每一列
返回值
- 上面在辅助节点已经说过了,返回值为dp[m][n]
完成上面的算法原理分析,下面我们来具体写一下代码
3 编写代码
class Solution {
public:int uniquePaths(int m, int n) {//开辟m*n的dp表vector<vector<int>>dp(m+1);for(int i=0;i<dp.size();i++){dp[i].resize(n+1,0);}dp[0][1]=1;//初始化//状态转移方程for(int i=1;i<=m;i++){for(int j=1;j<=n;j++)dp[i][j]=dp[i-1][j]+dp[i][j-1];}return dp[m][n];}
};
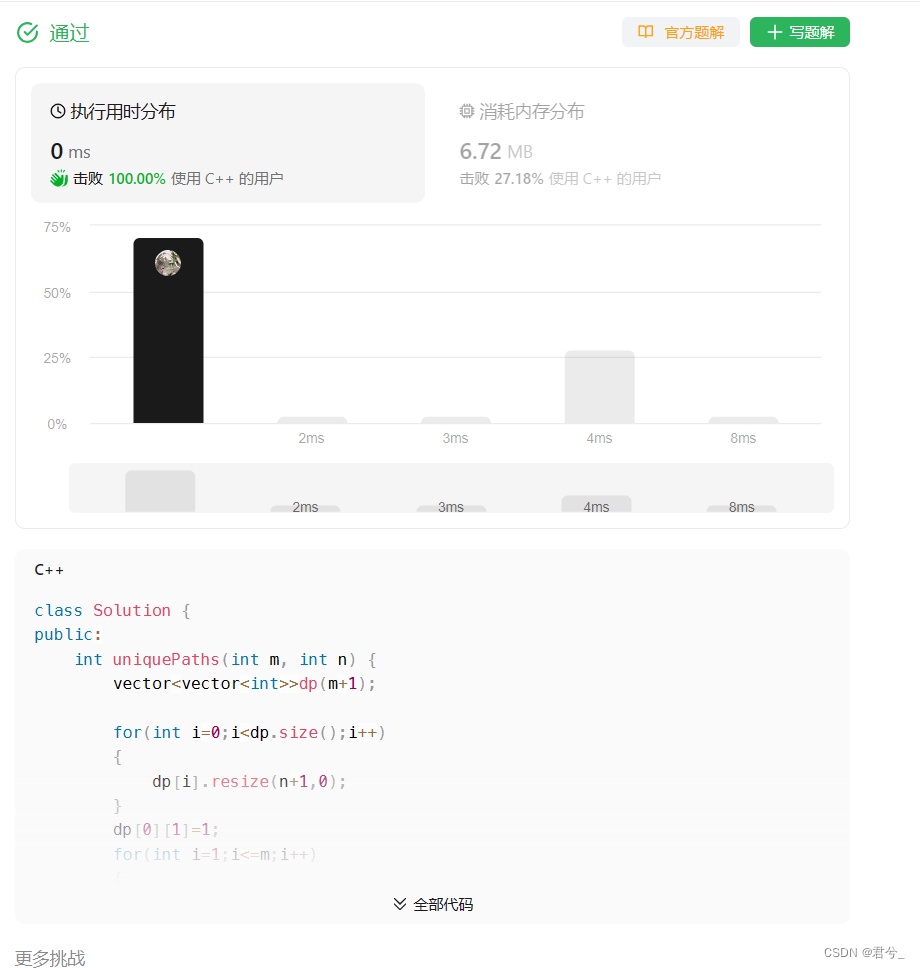
- 照这上面讲的算法原理一步一步照搬挺容易ac的,这里就不细讲了,重点还是放在下面这个题上
二 下降路径最小和
- 原题leetcode链接在这里 下降路径最小和
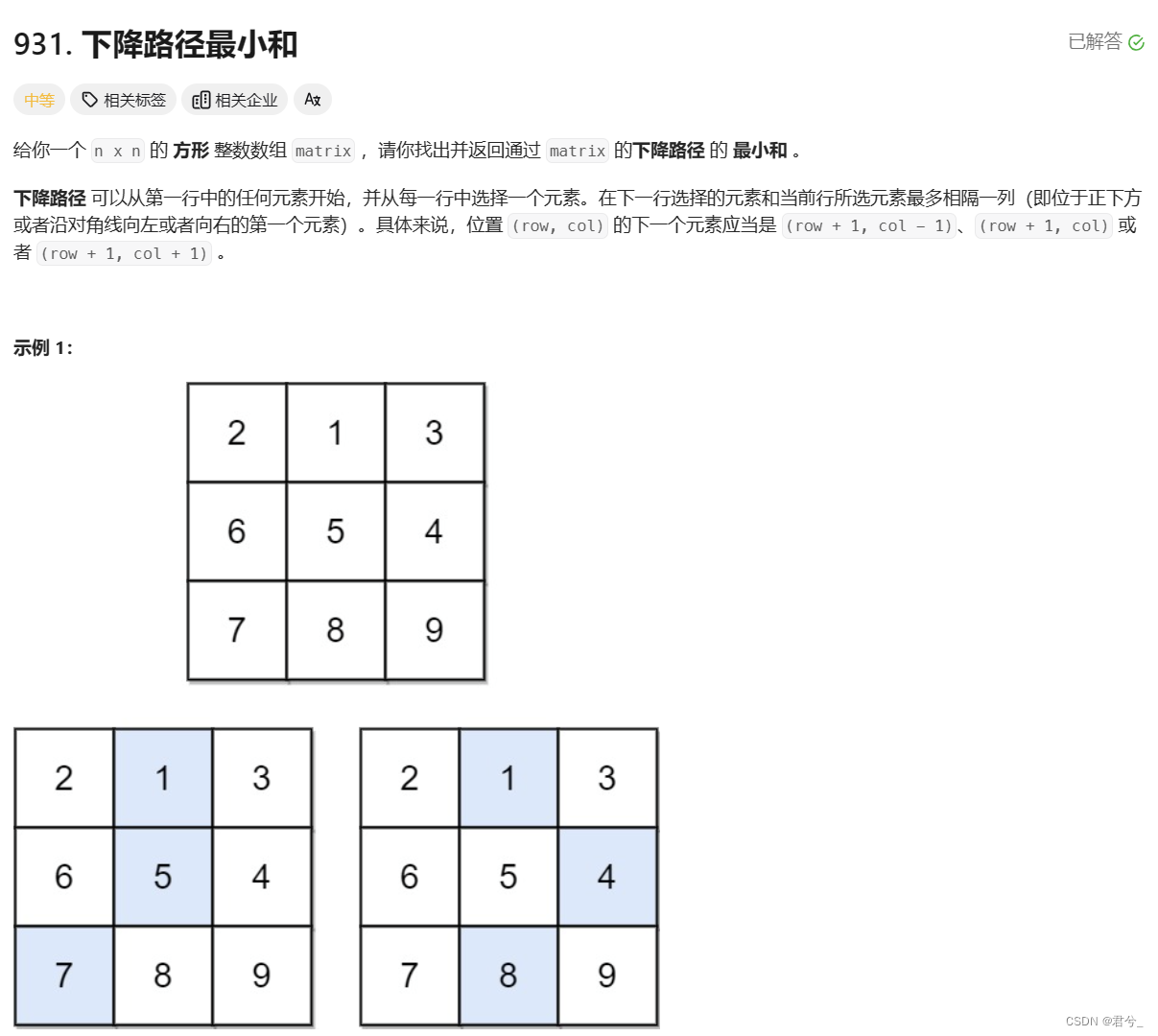
1 题目解析
- 给你一个 n x n 的方形整数数组 matrix ,请你找出并返回通过 matrix 的下降路径的最小和 。
- 下降路径可以从第一行中的任何元素开始,并从每一行中选择一个元素在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。具体来说,位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。
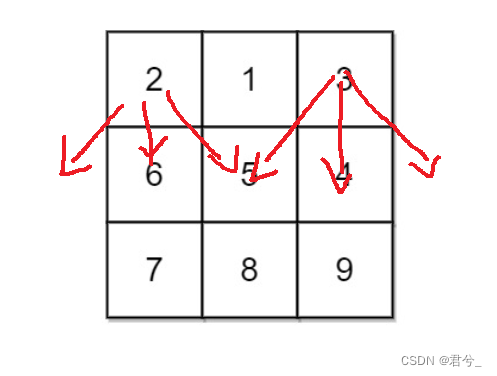
- 对于两边的特殊情况,只有向右和向左可供移动
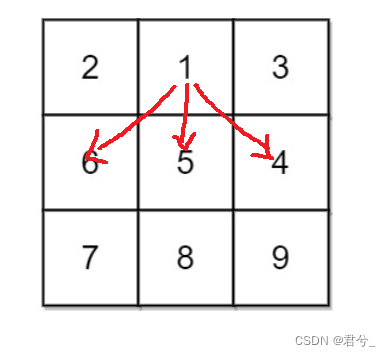
- 只有中间的情况,下一行三个位置均可插入
2 算法原理
- 一看到这种路径算不同种数啊,算最短呐,首先我们要有使用动态规划的想法
状态表示
- 对于这种「路径类」的问题,我们的状态表⽰⼀般有两种形式:
i. 从 [i, j] 位置出发,到达⽬标位置有多少种⽅式;
ii. 从起始位置出发,到达[i, j] 位置,⼀共有多少种⽅式
这⾥选择第⼆种定义状态表⽰的⽅式: - dp[i][j] 表示:到达[i, j] 位置时,所有下降路径中的最小和
- 路径问题的状态表示都是类似的,这里就不多阐释了,自己写的时候记得结合一下dp表中存的值符合题目要求就行
状态转移方程
- 先不考虑越界情况,对于普遍位置的dp[i, j] ,根据题意得,到达[i, j] 位置可能有三种情况:
i. 从正上⽅ [i - 1, j] 位置转移到 [i, j] 位置;
ii. 从左上⽅ [i - 1, j - 1] 位置转移到 [i, j] 位置;
iii. 从右上⽅ [i - 1, j + 1] 位置转移到 [i, j] 位置; - 我们要的是三种情况下的「最⼩值」,然后再加上数组中在 [i, j] 位置的值。
于是,我们可以得出状态转移方程
dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i - 1][j +1])) + matrix[i][j]
初始化
- 从我在题意分析中画的那个图,可以明显看出每一行的最左位置和最右位置都存在越界,因此为了防止出现这种情况,我们还是采用上面讲的辅助节点的方法来进行初始化,不同的是,此时两边都存在可能越界,因此我们要初始化一行两列,示意图如下:
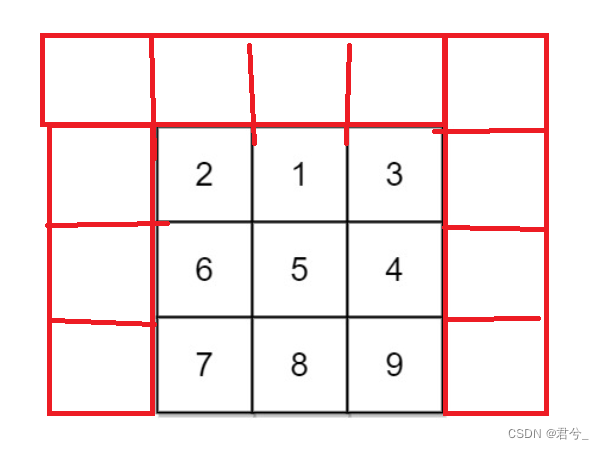
- 在这里对辅助节点进行初始化时,我们由于是求最小下降路径,为了不影响原dp表结果,此时先把辅助节点都填上一个较大的值。
- 此时,如果我们全都是较大的值,那么此时dp表第一行的初始化就会直接以这个较大值进行初始化,为了避免这种情况发生,我们将辅助节点的第一行全部初始化为0。
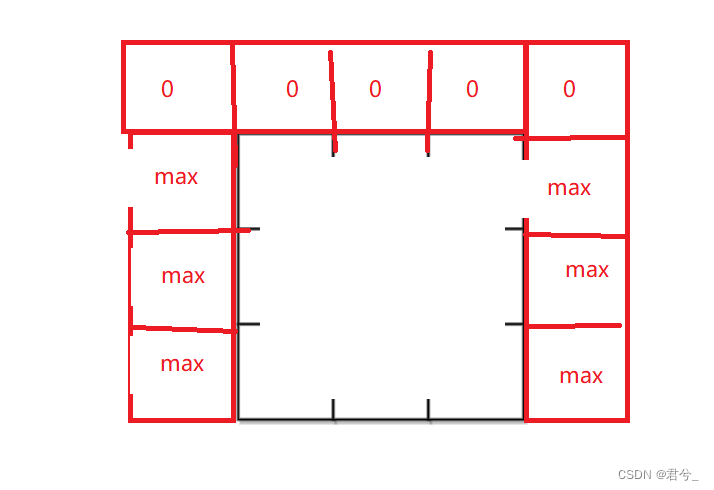
注意,重点来了: - 我们之前在辅助节点初始化方法中说过要注意下标的映射关系。
- 这里,我们需要把原数组的值填入到当前这个dp表中,但是现在的dp表多了一行两列,因此我们之前
dp[i][j]=min+matrix[i][j]就需要改成dp[i][j]=min+matrix[i-1][j-1],这样才能满足对应的下标关系
填表顺序
- 题目已经明确告诉你了。从上到下
返回值
- 注意这⾥不是返回 dp[m][n] 的值!
- 题⽬要求「只要到达最后⼀⾏」就⾏了,因此这⾥应该返回「dp表中最后⼀⾏的最⼩值」
3 编写代码
class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int n=matrix.size();//创建dp表vector<vector<int>>dp(n+1,vector<int>(n+2));//初始化for(int i=1;i<=n;i++){dp[i][0]=dp[i][n+1]=999999;}//填dp表for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){//状态转移方程int ret=min(dp[i-1][j],min(dp[i-1][j+1],dp[i-1][j-1]));//之前的值加上此时这里数组的值dp[i][j]=ret+matrix[i-1][j-1];}}//找最后一行的最小值int min1=dp[n][1];for(int i=2;i<=n;i++){if(dp[n][i]<min1)min1=dp[n][i];}return min1;}
};
- 照着上面的算法原理步骤走,ac不是so easy啦
总结
- 好啦,我们今天的内容就先到这里啦!向这种题光看是看到只能看个一知半解的,如果你想学好的话一定要自己认真把上面两个路径规划的题写好,光看很多算法中的细节是无法体会到的。
- 有任何的问题和对文章内容的疑惑欢迎在评论区中提出,当然也可以私信我,我会在第一时间回复的!!
新人博主创作不易,如果感觉文章内容对你有所帮助的话不妨三连一下再走呗。你们的支持就是我更新的动力!!!
**(可莉请求你们三连支持一下博主!!!点击下方评论点赞收藏帮帮可莉吧)**

相关文章:

【算法】动态规划中的路径问题
君兮_的个人主页 即使走的再远,也勿忘启程时的初心 C/C 游戏开发 Hello,米娜桑们,这里是君兮_,如果给算法的难度和复杂度排一个排名,那么动态规划算法一定名列前茅。今天,我们通过由简单到困难的两道题目带大家学会动…...

代数学笔记9: 群的直积,可解群,自由群,群表示
群的直积 外直积 H 1 , H 2 H_1,H_2 H1,H2是两个群(固定的群), 且有 G H 1 H 2 GH_1\times H_2 GH1H2,(构造的新群) G ( { ( h 1 , h 2 ) ∣ h 1 ∈ H 1 , h 2 ∈ H 2 } , ⋅ ) , G\big(\{(h_1,h_2)|h_1\in H_1,h_2\in H_2\},\cdot\big), G({(h1,h2)∣h1∈H…...
kali学习
目录 黑客法则: 一:页面使用基础 二:msf和Windows永恒之蓝漏洞 kali最强渗透工具——metasploit 介绍 使用永恒之蓝进行攻击 编辑 使用kali渗透工具生成远程控制木马 渗透测试——信息收集 域名信息收集 黑客法则: 一&…...

《论文阅读》DualGATs:用于对话中情绪识别的双图注意力网络
《论文阅读》DualGATs:用于会话中情感识别的双图注意力网络 前言摘要模型架构DisGAT图构建图关系类型图节点更新SpkGAT图构建图关系类型图节点更新交互模块情绪预测损失函数问题前言 今天为大家带来的是《DualGATs: Dual Graph Attention Networks...
【算法】单调栈题单——字典序最小⭐(一种类型的模板题)
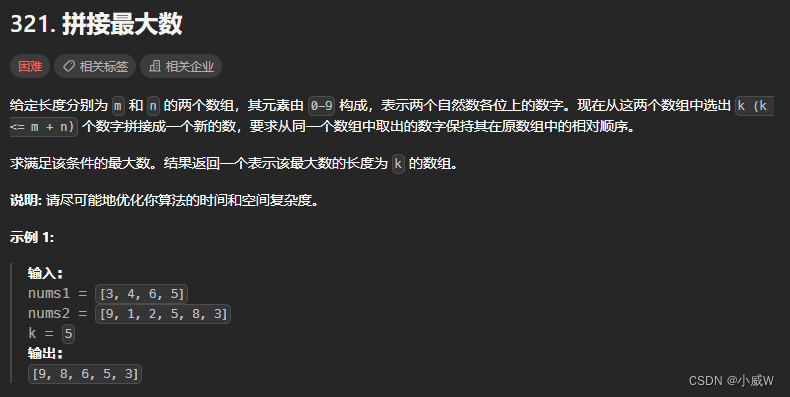
文章目录 题目列表316. 去除重复字母⭐⭐⭐⭐⭐(类型题模板:单调栈,字典序最小)221021天池-03. 整理书架(保留数量为 limit 的字典序最小)402. 移掉 K 位数字(最多删除 k 次 前导零的处理&…...
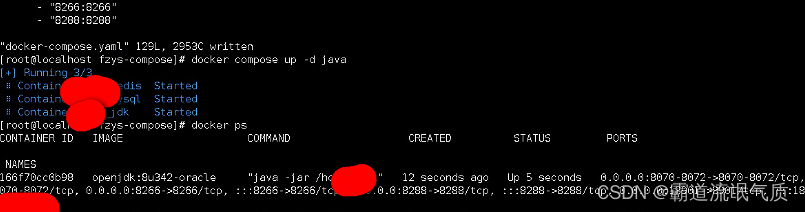
DockerCompose修改某个服务的配置(添加或编辑端口号映射)后如何重启单个服务使其生效
场景 docker-compose入门以及部署SpringBootVueRedisMysql(前后端分离项目)以若依前后端分离版为例: docker-compose入门以及部署SpringBootVueRedisMysql(前后端分离项目)以若依前后端分离版为例_docker-compose部署java mysql redis-CSDN博客 上面讲了docker c…...

DOM 事件的传播机制
前端面试大全DOM 事件的传播机制 🌟经典真题 🌟事件与事件流 事件流 事件冒泡流 事件捕获流 标准 DOM 事件流 🌟事件委托 🌟真题解答 🌟总结 🌟经典真题 谈一谈事件委托以及冒泡原理 dz…...

(数据结构)顺序表的查找
静态分配代码: #include<stdio.h> #include<stdlib.h> #define MAX 100 typedef struct LinkList {int data[MAX];int lenth; }Link; //初始化 void CreateList(Link* L) {L->lenth 0;for (int i 0; i < MAX; i){L->data[i] 0;} } //插入 …...

vue 解决响应大数据表格渲染崩溃问题
如果可以实现记得点赞分享,谢谢老铁~ 1.场景描述 发起请求获取上万条数据,进行表格渲染,使浏览器卡顿,导致网页崩溃。 2.分析原因 1.大量数据加载,过多操作Dom,消耗性能。 2.表格中包含其他…...
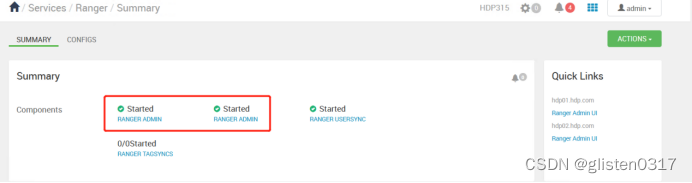
Hdoop学习笔记(HDP)-Part.13 安装Ranger
目录 Part.01 关于HDP Part.02 核心组件原理 Part.03 资源规划 Part.04 基础环境配置 Part.05 Yum源配置 Part.06 安装OracleJDK Part.07 安装MySQL Part.08 部署Ambari集群 Part.09 安装OpenLDAP Part.10 创建集群 Part.11 安装Kerberos Part.12 安装HDFS Part.13 安装Ranger …...

Spring AOP记录接口访问日志
Spring AOP记录接口访问日志 介绍应用范围组成通知(Advice)连接点(JoinPoint)切点(Pointcut)切面(Aspect)引入(Introduction)织入(Weaving&#x…...

分享89个节日PPT,总有一款适合您
分享89个节日PPT,总有一款适合您 89个节日PPT下载链接:https://pan.baidu.com/s/1j6Yj-7UCcUyV4V_S_eGjpQ?pwd6666 提取码:6666 Python采集代码下载链接:采集代码.zip - 蓝奏云 学习知识费力气,收集整理更不易…...

PostgreSQL日志中的SQL记录时机 —— log_statement 和 log_min_duration_statement
最近跟朋友讨论到PostgreSQL日志中的SQL记录时机,研究了下log_statement 和 log_min_duration_statement两个参数,记录一下。 一、 参数简介 1. log_statement ① 作用 控制记录SQL的类型,可选值为: none:关闭&…...
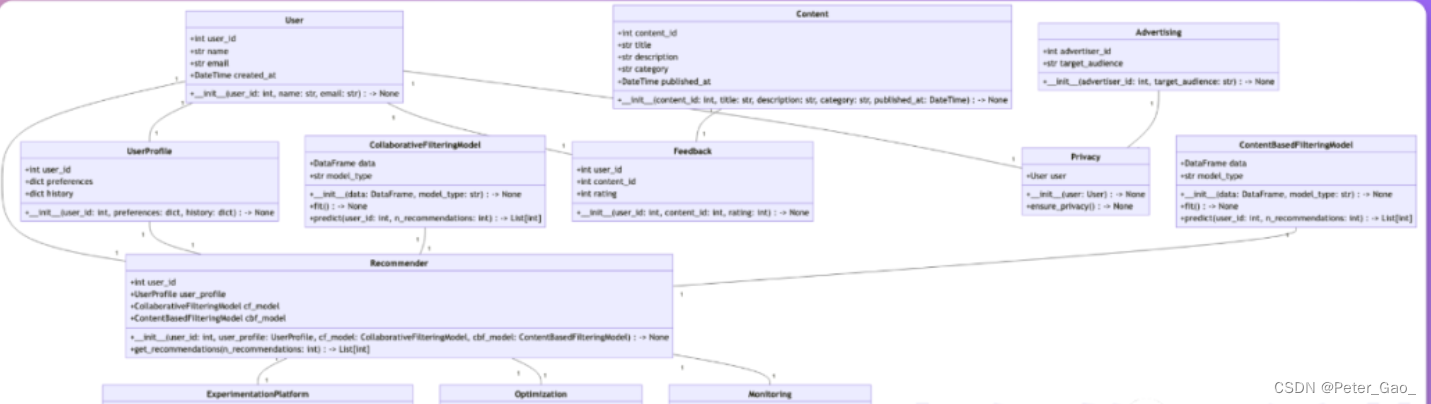
Agent举例与应用
什么是Agent OpenAI 应用研究主管 Lilian Weng 在一篇长文中提出了 Agent LLM(大型语言模型)记忆规划技能工具使用这一概念,并详细解释了Agent的每个模块的功能。她对Agent未来的应用前景充满信心,但也表明到挑战无处不在。 现…...
CentOS 7 配置tomcat
简介 Tomcat是一个使用Java编写的开源Web应用服务器,是由Apache Software Foundation管理的一个项目。它是一个轻量级的应用服务器,可以下载、安装和使用,而且还提供了许多高级功能,例如支持Java Servlet、JavaServer Pages (JSP)和JavaServer Faces (JSF) 等JavaEE技术,…...

如何优雅的关闭一个IIS站点
众所周知,当我们使用IIS的时候,在使用负载均衡的情况下,想停掉一个站点,通常会点击Sites(网站)中的Stop(停止)来停止一个站点。但是这样做,会带来一个问题,当…...

弱网模拟工具
一、背景 一个人晚上在家通过 Wi-Fi 上网,在线电影播放基本流畅,可一旦在晚间用网高峰期打视频电话就画面糊,这时不仅可能带宽受限了,还可能有较高的丢包率。与有线网络通信相比,无线网络通信受环境影响会更大&#x…...
)
Leetcode 第 110 场双周赛 Problem D 2809. 使数组和小于等于 x 的最少时间(DP+贪心+正难则反)
Leetcode 第 110 场双周赛 Problem D 2809. 使数组和小于等于 x 的最少时间(DP 好题)题目 给你两个长度相等下标从 0 开始的整数数组 nums1 和 nums2 。每一秒,对于所有下标 0 < i < nums1.length ,nums1[i] 的值都增加 num…...
已知数组A[1..n]中元素类型为非负整数,设计算法将其调整为左右两部分,左边所有为奇数,右边所有为偶数,并要求算法的时间复杂度为O(n)
//左边奇数右边偶数 void Swap(int* a, int* b) {int tmp *b;*b *a;*a tmp; } void LeftRight(int arr[],int n) {int i 0;int j n - 1;while(i<j){if (arr[i] % 2 0 && arr[j] % 2 1) {Swap(&arr[i], &arr[j]);i;j--;}else if (arr[i] % 2 1 &…...
ssm+vue的罪犯信息管理系统(有报告)。Javaee项目,ssm vue前后端分离项目。
演示视频: ssmvue的罪犯信息管理系统(有报告)。Javaee项目,ssm vue前后端分离项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构&…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
