【动态规划】LeetCode-746LCR 088.使用最小花费爬楼梯
🎈算法那些事专栏说明:这是一个记录刷题日常的专栏,每个文章标题前都会写明这道题使用的算法。专栏每日计划至少更新1道题目,在这立下Flag🚩
🏠个人主页:Jammingpro
📕专栏链接:算法那些事
🎯每日学习一点点,技术累计看得见
题目
题目描述
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
执行示例
示例 1:
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。
总花费为 15 。
示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
提示
2 <= cost.length <= 1000
0 <= cost[i] <= 999
题解
由题目可知,如果想爬到第n个台阶,可以从n-1号台阶爬1个台阶到达,也可以从n-2号台阶爬2个台阶到达。我们只要求出这两个台阶的花费,从中选择小的那个,就可以得到爬到第n个台阶的花费,即sumCost[n]=min{sumCost[n-1], sumCost[n-2]} + cost[n]。
以示例1为例,爬到下标为0的台阶的花费为10,即从开始的地方爬到第1号台阶到达,因而sumCost[0]=10;爬到下标为1的台阶的花费为15,即从开始的地方爬2个台阶到达或从0号台阶爬1个台阶到达,因而sumCost[1]=min{sumCost[0], 0}+cost[1]=0+15=15;爬到下标为2的她姐的花费为30,因为sumCost[2]=min{sumCost[1], sumCost[0]}+cost[2]=10+20=30;爬到楼梯顶部的花费=min{sumCost[2], sumCost[1]}=15。
通过上面的分析,我们得到了状态转移方程(也叫做递推公式),那么我们就可以开始编码了↓↓↓
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();vector<int>dp(n);dp[0] = cost[0];dp[1] = cost[1];for(int i = 2; i < n; i++)dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];return min(dp[n - 1], dp[n - 2]);}
};
这种解法的时空复杂度均为O(N),可以通过滚动数组的方式,将其空间复杂度将为O(1)。我们设置3个变量cur、pre、ppre,分别保存当前台阶花费和前两个台阶的花费。
ps:ppre初始化为cost[0],pre初始化为cost[1],cur初始化为min{cosy[0], cost[1]} + cost[2],这3步初始化,求出了0号、1号、2号台阶的最小花费。通过ppre=pre和pre=cur操作后,ppre、pre分别保存的是第1号和第2号台阶的最小花费,通过cur=min(ppre,pre)+cost[3]可计算出第3号台阶的最小花费。以此类推…
代码实现如下↓↓↓
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();if(n == 2) return min(cost[0], cost[1]);int ppre = cost[0], pre = cost[1], cur = min(cost[0], cost[1]) + cost[2];for(int i = 3; i < n; i++){ppre = pre;pre = cur;cur = min(ppre, pre) + cost[i];}return min(pre, cur);}
};
本文存在不足,欢迎留言或私信批评、指正。希望我的解决方法能够对你有所帮助~~
今日打卡完成,点亮小星星☆→★
相关文章:

【动态规划】LeetCode-746LCR 088.使用最小花费爬楼梯
🎈算法那些事专栏说明:这是一个记录刷题日常的专栏,每个文章标题前都会写明这道题使用的算法。专栏每日计划至少更新1道题目,在这立下Flag🚩 🏠个人主页:Jammingpro 📕专栏链接&…...

Unity 接入TapADN播放广告时闪退 LZ4JavaSafeCompressor
通过跟踪安卓日志,发现报如下错误 Didnt find class "com.tapadn.lz4.LZ4JavaSafeCompressor" 解决方案: 去掉Minify这边的勾选,再打包即可。...

【九】linux下部署frp客户端服务端实践(内网穿透)
linux下部署frp客户端服务端实践 简介: 今天有一个这样的需求,部署在公司内部局域网虚拟机上的服务需要在外网能够访问到,这不就是内网穿透的需求吗,之前通过路由器实现过,现在公司这块路由器不具备这个功能了&#x…...
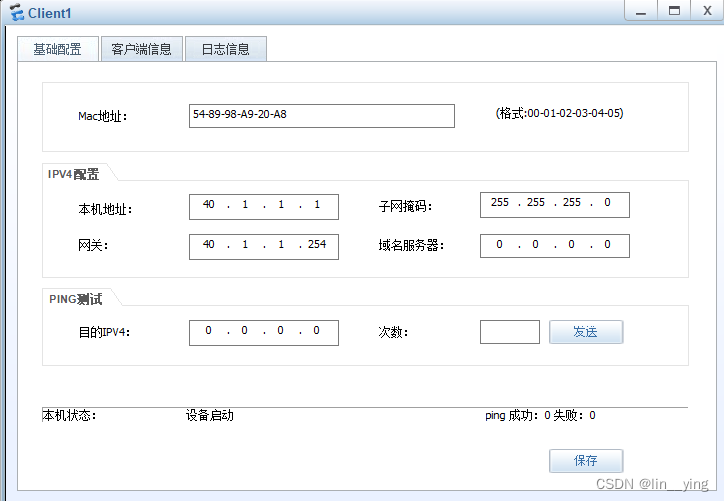
华为1+x网络系统建设与运维(中级)-练习题2
一.设备命令 LSW1 [Huawei]sys LSW1 同理可得,给所有设备改名 二.VLAN LSW1 [LSW1]vlan ba 10 20 [LSW1]int g0/0/1 [LSW1-GigabitEthernet0/0/1]port link-type trunk [LSW1-GigabitEthernet0/0/1]port trunk allow-pass vlan 10 20 [LSW1-GigabitEthernet0/0/1]in…...
自定义类型-结构体,联合体和枚举-C语言
引言 能看到结构体,说明C语言想必学习的时间也不少了,在之前肯定也学习过基本数据类型,包括整型int,浮点型float等等。可是在日常生活中,想要描述一个事物并没有那么简单。比如,你要描述一本书,…...

Windows 安装redis,设置开机自启动
Windows 安装redis,设置开机自启动 文章目录 Windows 安装redis,设置开机自启动下载, 解压到指定目录设置redis密码启动redis服务端停止redis服务端设置自启动 下载, 解压到指定目录 官网地址: https://redis.io/ 安装包下载地址: https://github.com/tporadowski/redis/relea…...

Windows安装Mysql Workbench及常用操作
Mysql Workbench是mysql自带的可视化操作界面,功能是强大的,但界面和navicat比,就是觉得别扭,但其实用惯了也还好,各有特色吧。这里记录一下常用的操作。 官方手册:MySQL Workbench 一、安装 1. 下载 官方…...
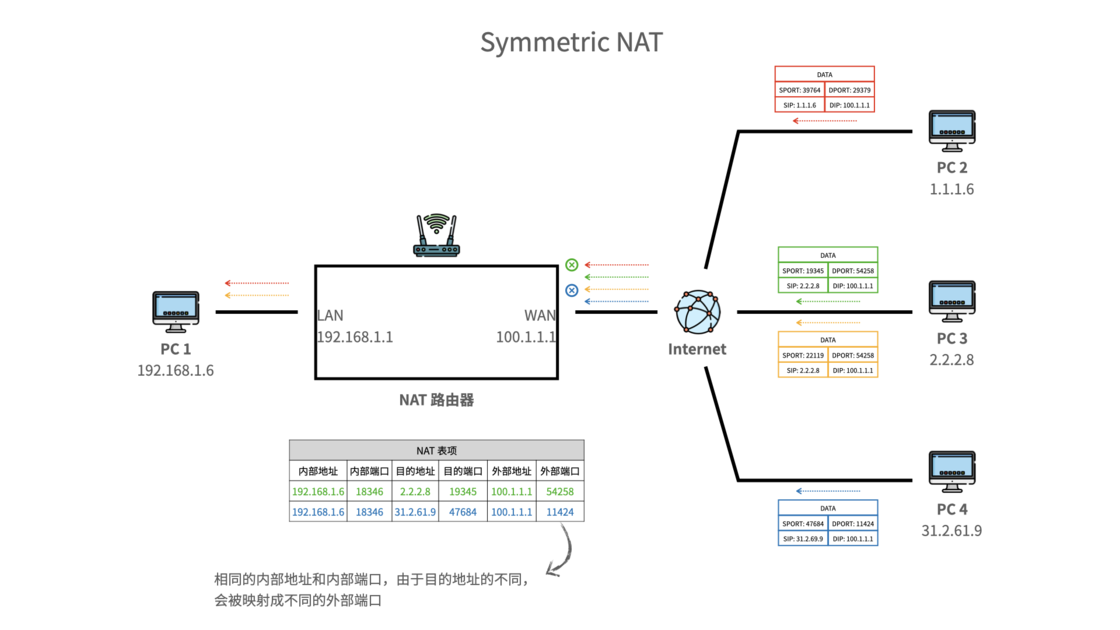
【计算机网络】15、NAT、NAPT 网络地址转换、打洞
文章目录 一、概念二、分类(主要是传统 NAT)2.1 基本 NAT2.2 NAPT 三、访问NAT下的内网设备的方式3.1 多拨3.2 端口转发、DMZ3.3 UPnP IGD、NAT-PMP3.4 服务器中转:frp 内网穿透3.4.1 NAT 打洞3.4.2 NAT 类型与打洞成功率3.4.2.1 完全圆锥形 …...

【送书活动三期】解决docker服务假死问题
工作中使用docker-compose部署容器,有时候会出现使用docker-compose stop或docker-compose down命令想停掉容器,但是依然无法停止或者一直卡顿在停止中的阶段,这种问题很让人头疼啊! 目录 问题描述问题排查问题解决终极杀招-最粗暴…...

【每日一题】拼车+【差分数组】
文章目录 Tag题目来源解题思路方法一:差分 写在最后 Tag 【差分数组】【数组】【2023-12-02】 题目来源 1094. 拼车 解题思路 本题朴素的解题思路是统计题目中提到的每一个站点的车上人数,如果某个站点的车上人数大于车上的座位数直接返回 false&…...

【开源】基于JAVA的农村物流配送系统
项目编号: S 024 ,文末获取源码。 \color{red}{项目编号:S024,文末获取源码。} 项目编号:S024,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 系统登录、注册界面2.2 系统功能2.2…...
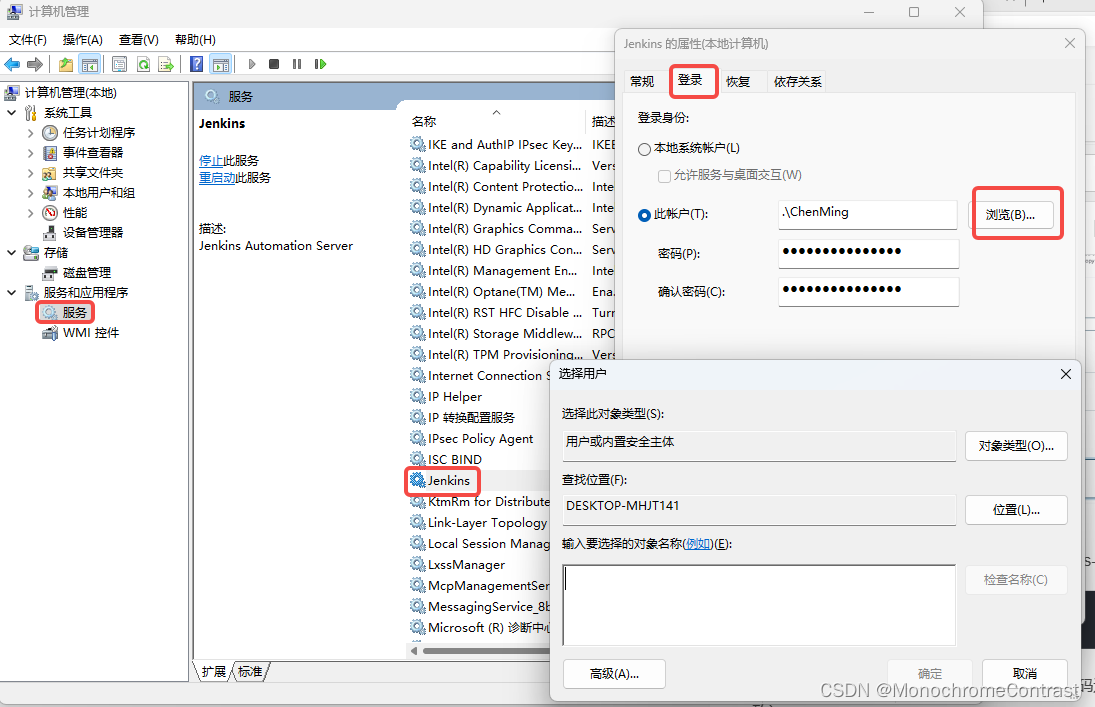
7、Jenkins+Nexus3+Docker+K8s实现CICD
文章目录 基本环境配置一、Jenkins安装必要插件二、Jenkins系统配置三、新建流水线四、在项目工程里添加Jenkinsfile、deploy.yml五、在项目工程里添加Dockerfile在这里插入图片描述 总结 提示:本章主要记录各基本环境搭建好后如何配置Jenkins流水线部署微服务到K8s…...
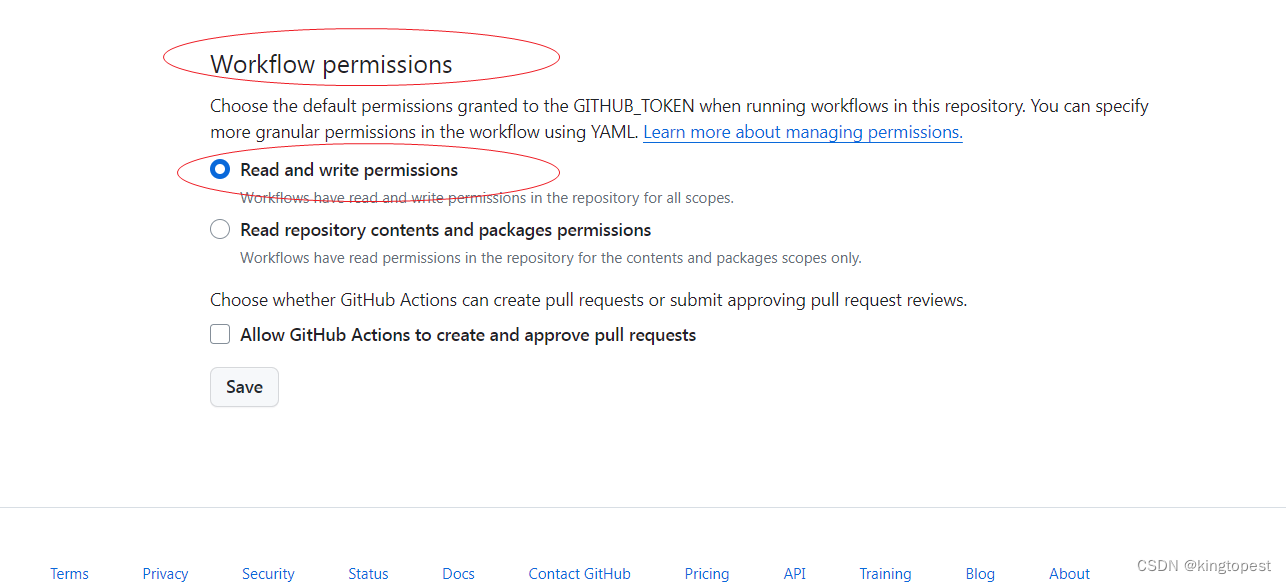
解决git action发布失败报错:Error: Resource not accessible by integration
现象: 网上说的解决方法都是什么到github个人中心setting里面的action设置里面去找。 可这玩意根本就没有! 正确解决办法: 在你的仓库页面,注意是仓库页面的setting里面: Actions> General>Workflow permisss…...

[传智杯 #2 决赛] 补刀
题目描述 UIM 在写程序的空闲玩一款 MOBA 游戏。 当敌方的小兵进入到我方防御塔的范围内,就会持续受到防御塔造成的伤害;当然我方英雄也可以对它造成伤害。当小兵的血量降到了 0 或者更低,就会被击杀。为了获得经验,UIM 希望在防…...

C语言:求Sn=a+aa+aaa+aaaa+……(n个a)之值,其中a表示一个数字,n表示a的位数,n由键盘录入。
分析: 在主函数 main 中,程序首先定义四个整型变量 a、n、i 和 sn,并初始化 a、n 和 i 的值,其中 sn 用于记录数列的和。然后使用 scanf 函数从标准输入中读取用户输入的两个整数 a 和 n。 接下来,程序通过 while …...
)
【nlp】4.1 fasttext工具介绍(文本分类、训练词向量、词向量迁移)
fasttext工具介绍与文本分类 1 fasttext介绍1.1 fasttext作用1.2 fasttext工具包的优势1.3 fasttext的安装1.4 验证安装2 fasttext文本分类2.1 文本分类概念2.2 文本分类种类2.3 文本分类的过程2.4 文本分类代码实现2.4.1 获取数据2.4.2 训练集与验证集的划分2.4.3 训练模型2.4…...

Spring中的事务管理
1 基本概念 事务:将一组操作抽象成一个不可再分的单位,这组操作可以有很多个,但是它们要么就全部都执行成功,这时算作事务执行成功;要不其中有操作执行失败,则其余操作都视为执行失败,这时候需…...

量子光学的进步:光子学的“下一件小事”
量子光学是量子力学和光学交叉领域中发展迅速的一门学科,探索光的基本特性及其与物质在量子水平上的相互作用。通过利用光的独特特性,量子光学为通信、计算、密码学和传感等各个学科的变革性进步铺平了道路。 如今,量子光学领域的研究人员和工…...

微信小程序获取定位显示在百度地图上位置出现偏差
项目场景: 背景: 微信小程序端获取手机定位坐标,以及正确展示位置通过详细地址解析为定位坐标显示在小程序端以及PC后台小程序获取的地理坐标与百度地图坐标相互转化 相关知识 目前国内主要有以下三种坐标系: WGS84:…...
 数据结构设计)
【LeetCode 0170】【哈希】两数之和(3) 数据结构设计
https://leetcode.com/problems/two-sum-iii-data-structure-design/ 描述 Design and implement a TwoSum class. It should support the following operations: add and find. add(input) – Add the number input to an internal data structure. find(value) – Find if …...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...
