【每日一题】拼车+【差分数组】
文章目录
- Tag
- 题目来源
- 解题思路
- 方法一:差分
- 写在最后
Tag
【差分数组】【数组】【2023-12-02】
题目来源
1094. 拼车

解题思路
本题朴素的解题思路是统计题目中提到的每一个站点的车上人数,如果某个站点的车上人数大于车上的座位数直接返回 false,如果直到行程结束都没有返回 false,则直接返回 true。朴素方法的时间复杂度为 O ( n 2 ) O(n^2) O(n2), n n n 最大为 1000,该方法时间复杂度较高但是可以通过本题。
接下来将会介绍一种时间复杂度较优的方法,时间复杂度为 O ( n + U ) O(n + U) O(n+U)。
方法一:差分
我们先来看一下,朴素方法的实现代码:
class Solution {
public:bool carPooling(vector<vector<int>>& trips, int capacity) {vector<int> peoples(10010);for (auto trip : trips) {for (int i = trip[1]; i < trip[2]; ++i) {peoples[i] += trip[0];if (peoples[i] > capacity) {return false;}}}return true;}
};
注意观察朴素解法中对于数组 peoples 的更新,我们枚举并更新所有站点的车上人数,朴素方法的时间复杂度较高的原因就是此处的嵌套枚举更新人数。此处可以使用【差分数组】来优化时间复杂度。
什么是差分数组?
差分数组是一个与原数组长度相同的数组,其中,除了首元素,其余的每个元素都是原数组中相邻两个元素的差值。比如数组 arr = [1, 4, 5, 6] 的差分数组 diff = [1, 3, 1, 1],数组 arr[i] = diff[0, ..., i],即原数组 arr 中的第 i 个元素等于差分数组 diff 第 0 到第 i 个元素之和。
时间是如何优化的?
对于某一段旅行有 numPassengers 乘客,乘客上车点为 from,下车点为 to,这一段旅程的我们只需要更新差分数数组的两个位置对应的值,即更新乘客上车点 diff[from] += numPaaengers, 更新乘客下车点 diff[to] -= numPaaengers。此时的时间复杂度为 O ( 2 × n ) = O ( n ) O(2 \times n) = O(n) O(2×n)=O(n), n n n 为数组 trips 的长度。
然后,利用差分数组累加得到每个站点的车上人数,并与 capacity 比较,… 此处的时间复杂度为 O ( U ) O(U) O(U), U = m a x ( t o i ) U = max(to_i) U=max(toi)。
我们借助差分数组将嵌套枚举转化为了两个线性枚举,大大降低了时间复杂度。
实现代码
class Solution {
public:bool carPooling(vector<vector<int>>& trips, int capacity) {int d[1001];memset(d, 0, sizeof(d));for (auto trip : trips) {int num = trip[0], from = trip[1], to = trip[2];d[from] += num;d[to] -= num;}int s = 0;for (int v : d) {s += v;if (s > capacity) {return false;}}return true;}
};
复杂度分析
时间复杂度: O ( n + U ) O(n + U) O(n+U), n n n 为数组 trips 的长度, U = m a x ( t o i ) U = max(to_i) U=max(toi)。
空间复杂度: O ( U ) O(U) O(U)。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【每日一题】拼车+【差分数组】
文章目录 Tag题目来源解题思路方法一:差分 写在最后 Tag 【差分数组】【数组】【2023-12-02】 题目来源 1094. 拼车 解题思路 本题朴素的解题思路是统计题目中提到的每一个站点的车上人数,如果某个站点的车上人数大于车上的座位数直接返回 false&…...

【开源】基于JAVA的农村物流配送系统
项目编号: S 024 ,文末获取源码。 \color{red}{项目编号:S024,文末获取源码。} 项目编号:S024,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 系统登录、注册界面2.2 系统功能2.2…...
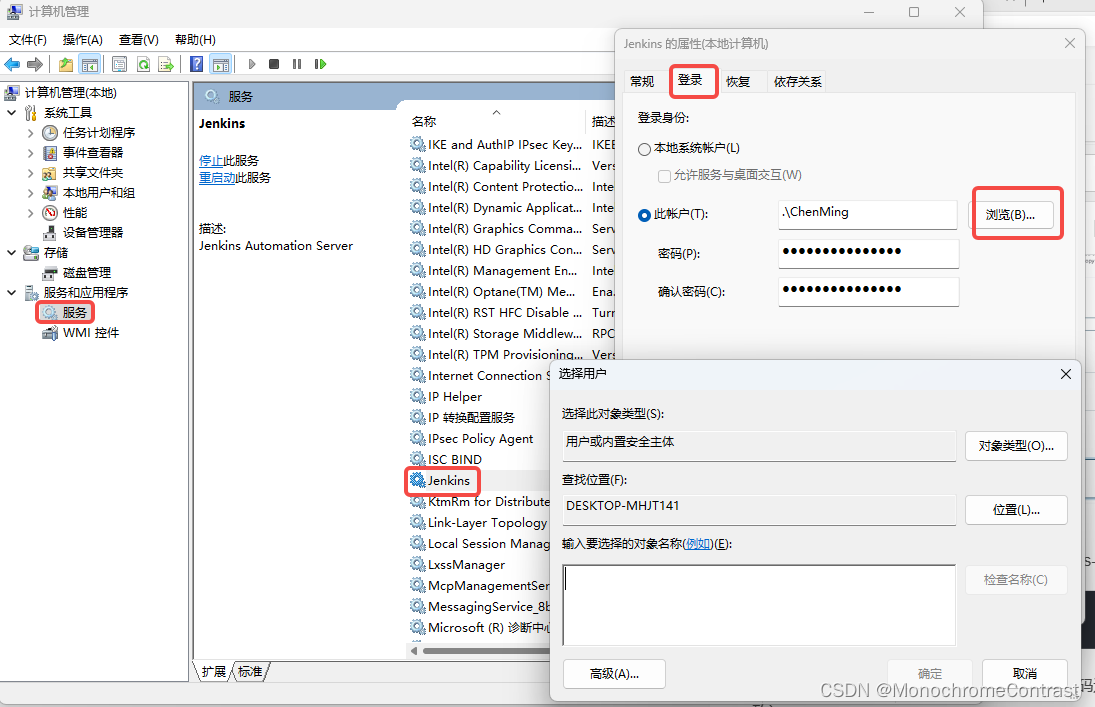
7、Jenkins+Nexus3+Docker+K8s实现CICD
文章目录 基本环境配置一、Jenkins安装必要插件二、Jenkins系统配置三、新建流水线四、在项目工程里添加Jenkinsfile、deploy.yml五、在项目工程里添加Dockerfile在这里插入图片描述 总结 提示:本章主要记录各基本环境搭建好后如何配置Jenkins流水线部署微服务到K8s…...
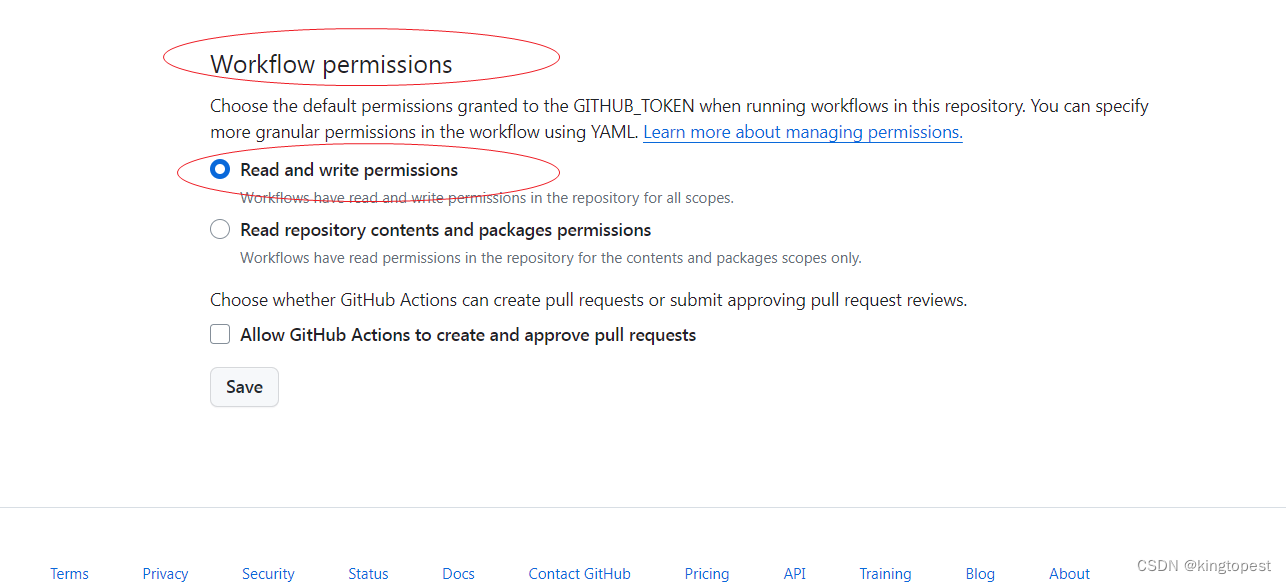
解决git action发布失败报错:Error: Resource not accessible by integration
现象: 网上说的解决方法都是什么到github个人中心setting里面的action设置里面去找。 可这玩意根本就没有! 正确解决办法: 在你的仓库页面,注意是仓库页面的setting里面: Actions> General>Workflow permisss…...

[传智杯 #2 决赛] 补刀
题目描述 UIM 在写程序的空闲玩一款 MOBA 游戏。 当敌方的小兵进入到我方防御塔的范围内,就会持续受到防御塔造成的伤害;当然我方英雄也可以对它造成伤害。当小兵的血量降到了 0 或者更低,就会被击杀。为了获得经验,UIM 希望在防…...

C语言:求Sn=a+aa+aaa+aaaa+……(n个a)之值,其中a表示一个数字,n表示a的位数,n由键盘录入。
分析: 在主函数 main 中,程序首先定义四个整型变量 a、n、i 和 sn,并初始化 a、n 和 i 的值,其中 sn 用于记录数列的和。然后使用 scanf 函数从标准输入中读取用户输入的两个整数 a 和 n。 接下来,程序通过 while …...
)
【nlp】4.1 fasttext工具介绍(文本分类、训练词向量、词向量迁移)
fasttext工具介绍与文本分类 1 fasttext介绍1.1 fasttext作用1.2 fasttext工具包的优势1.3 fasttext的安装1.4 验证安装2 fasttext文本分类2.1 文本分类概念2.2 文本分类种类2.3 文本分类的过程2.4 文本分类代码实现2.4.1 获取数据2.4.2 训练集与验证集的划分2.4.3 训练模型2.4…...

Spring中的事务管理
1 基本概念 事务:将一组操作抽象成一个不可再分的单位,这组操作可以有很多个,但是它们要么就全部都执行成功,这时算作事务执行成功;要不其中有操作执行失败,则其余操作都视为执行失败,这时候需…...

量子光学的进步:光子学的“下一件小事”
量子光学是量子力学和光学交叉领域中发展迅速的一门学科,探索光的基本特性及其与物质在量子水平上的相互作用。通过利用光的独特特性,量子光学为通信、计算、密码学和传感等各个学科的变革性进步铺平了道路。 如今,量子光学领域的研究人员和工…...

微信小程序获取定位显示在百度地图上位置出现偏差
项目场景: 背景: 微信小程序端获取手机定位坐标,以及正确展示位置通过详细地址解析为定位坐标显示在小程序端以及PC后台小程序获取的地理坐标与百度地图坐标相互转化 相关知识 目前国内主要有以下三种坐标系: WGS84:…...
 数据结构设计)
【LeetCode 0170】【哈希】两数之和(3) 数据结构设计
https://leetcode.com/problems/two-sum-iii-data-structure-design/ 描述 Design and implement a TwoSum class. It should support the following operations: add and find. add(input) – Add the number input to an internal data structure. find(value) – Find if …...
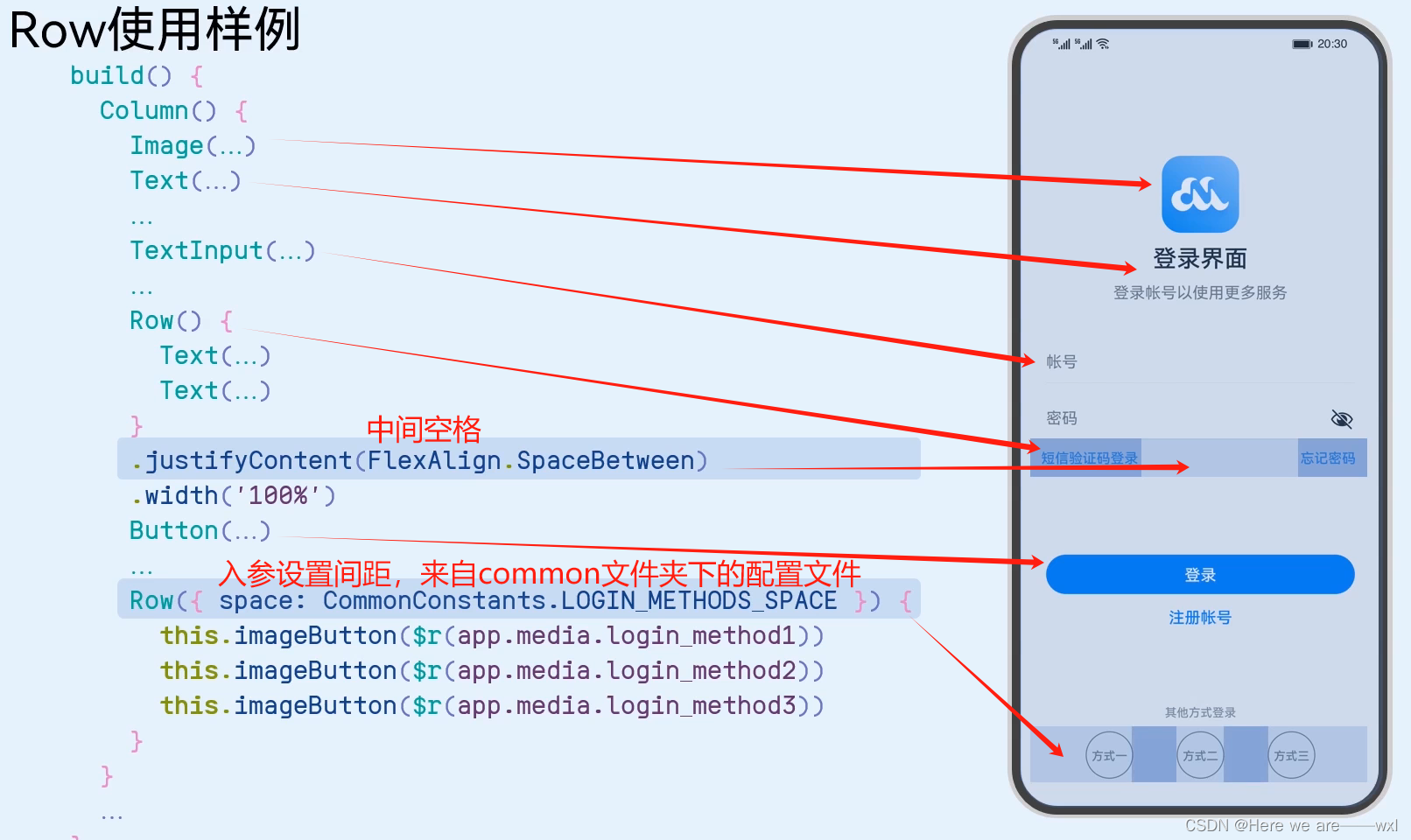
005、简单页面-容器组件
之——布局 目录 之——布局 杂谈 正文 1.布局基础知识 2.Column 3.Row 4.实践 杂谈 布局容器组件。 一个丰富的页面需要很多组件组成,那么,我们如何才能让这些组件有条不紊地在页面上布局呢?这就需要借助容器组件来实现。 容器组件是…...

stm32中断调用流程
USART1_IRQHandler(void)(中断服务函数) -> HAL_UART_IRQHandler(UART_HandleTypeDef *huart)(中断处理函数) -> UART_Receive_IT(UART_HandleTypeDef *huart) (接收函数) -> HAL_UART_RxCpltCallback(huart);(中断回调函数) HAL_UART_IRQHandler(UART_HandleTypeDef…...
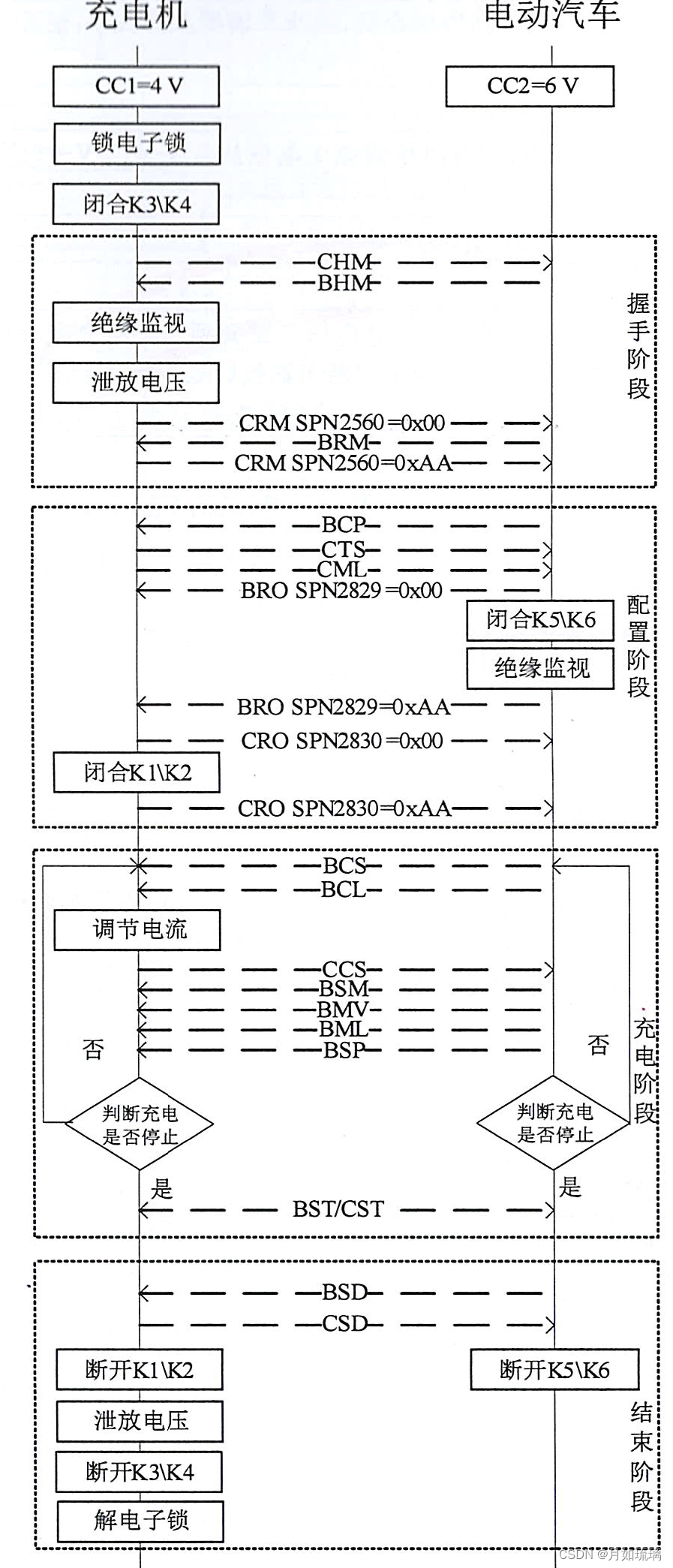
18487.1 - 2015 电动汽车充电系统标准 第1部分 关键点梳理
一、部分知识介绍 1、连接方式 使用电缆和连接器将电动汽车接入电网(电源)的方法。 1.1、连接方式A 1.2、连接方式B 1.3、连接方式C 2、电动汽车控电设备 2.1、按照输出电压分类 1)交流 单相 220V,三相 380V. 2)…...
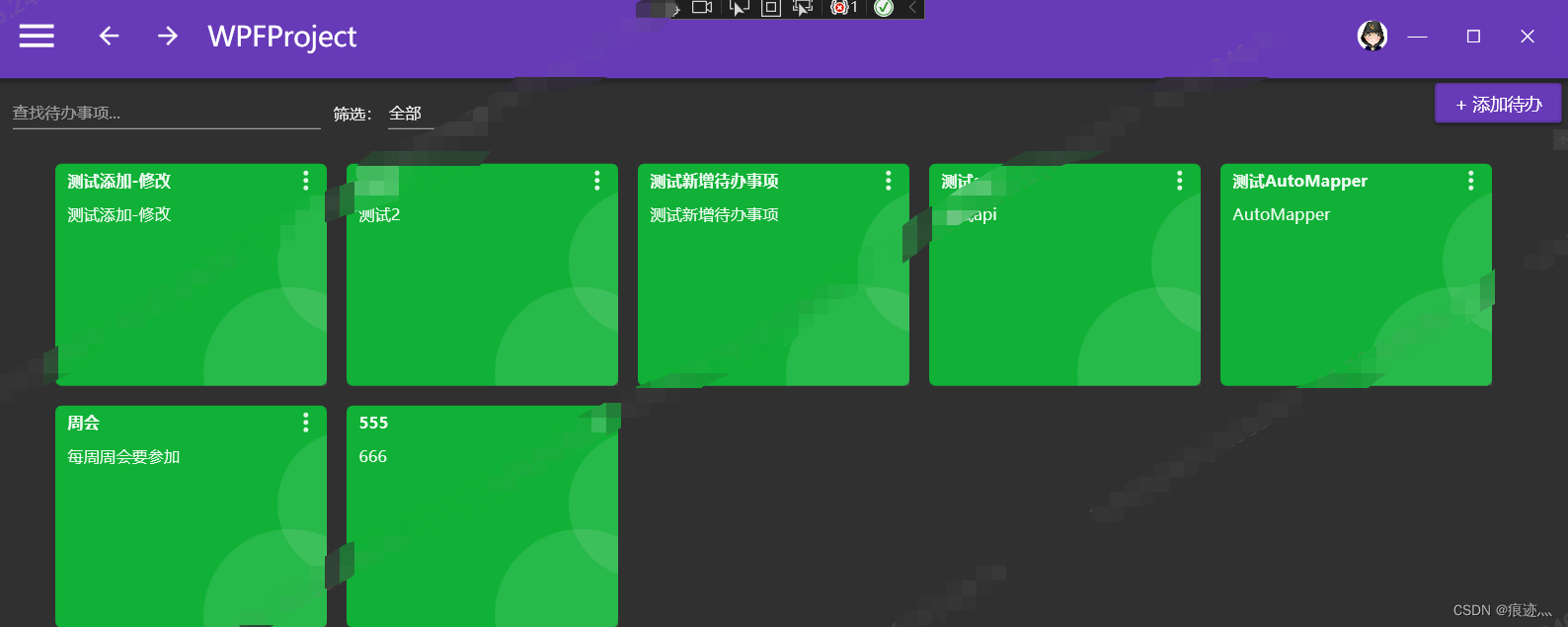
WPF实战项目十八(客户端):添加新增、查询、编辑功能
1、ToDoView.xmal添加引用,添加微软的行为类 xmlns:i"http://schemas.microsoft.com/xaml/behaviors" 2、给项目添加行为 <i:Interaction.Triggers><i:EventTrigger EventName"MouseLeftButtonUp"><i:InvokeCommandAction Com…...
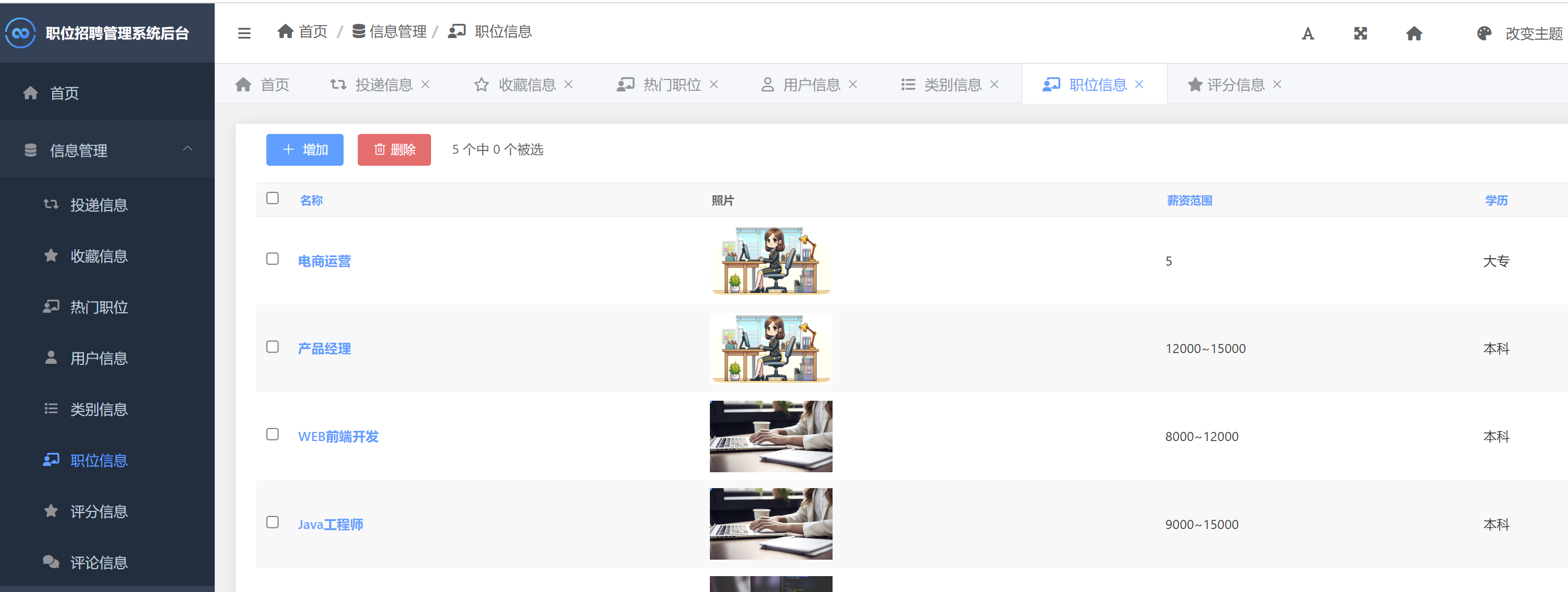
职位招聘管理与推荐系统Python+Django网页界面+协同过滤推荐算法
一、介绍 职位招聘管理与推荐系统。本系统使用Python作为主要开发语言,以WEB网页平台的方式进行呈现。前端使用HTML、CSS、Ajax、BootStrap等技术,后端使用Django框架处理用户请求。 系统创新点:相对于传统的管理系统,本系统使用…...
C#文件流二进制文件的读写
目录 一、BinaryWriter类 二、BinaryReader类 三、示例 1.源码 2.生成效果 二进制文件的写入与读取主要是通过BinaryWriter类和BinaryReader类来实现的。 一、BinaryWriter类 BinaryWriter类以二进制形式将基元类型写入流,并支持用特定的编码写入字符串&#…...
如何正确选择爬虫采集接口和API?区别在哪里?
在信息时代,数据已经成为了一个国家、一个企业、一个个人最宝贵的资源。而爬虫采集接口则是获取这些数据的重要手段之一。本文将从以下八个方面进行详细讨论: 1.什么是爬虫采集接口? 2.爬虫采集接口的作用和意义是什么? 3.爬虫…...
k8s部署jenkins
1.先决条件 1.因为国内的容器镜像加速器无法实时更新docker hub上的镜像资源.所以可以自己进行jenkins的容器镜像创建,. 2.这里用到了storageClass k8s的动态制备.详情参考: k8s-StoargClass的使用-基于nfs-CSDN博客 3.安装docker服务.(用于构建docker image) 2.构建jenki…...

HTTP相关
HTTP 什么是http - 蘑菇声活 http特点 1.基于TCP协议之上的应用层协议 2.基于请求--响应 3.无状态(每次发送请求对服务端都是新的) 4.无/短连接(客户端不会一直跟服务端连接) http请求协议与响应协议 请求协议 请求首行&…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...
