Leetcode.1223 掷骰子模拟
题目链接
Leetcode.1223 掷骰子模拟 Rating : 2008
题目描述
有一个骰子模拟器会每次投掷的时候生成一个 1 到 6 的随机数。
不过我们在使用它时有个约束,就是使得投掷骰子时,连续 掷出数字 i 的次数不能超过 rollMax[i](i 从 1 开始编号)。
现在,给你一个整数数组 rollMax和一个整数 n,请你来计算掷 n次骰子可得到的不同点数序列的数量。
假如两个序列中至少存在一个元素不同,就认为这两个序列是不同的。由于答案可能很大,所以请返回 模 10^9 + 7之后的结果。
示例 1:
输入:n = 2, rollMax = [1,1,2,2,2,3]
输出:34
解释:我们掷 2 次骰子,如果没有约束的话,共有 6 * 6 = 36 种可能的组合。但是根据 rollMax 数组,数字 1 和 2 最多连续出现一次,所以不会出现序列 (1,1) 和 (2,2)。因此,最终答案是 36-2 = 34。
示例 2:
输入:n = 2, rollMax = [1,1,1,1,1,1]
输出:30
示例 3:
输入:n = 3, rollMax = [1,1,1,2,2,3]
输出:181
提示:
- 1<=n<=50001 <= n <= 50001<=n<=5000
- rollMax.length==6rollMax.length == 6rollMax.length==6
- 1<=rollMax[i]<=151 <= rollMax[i] <= 151<=rollMax[i]<=15
分析:
使用 动态规划 的方式求解。
我们定义 f(i,j,times)f(i,j,times)f(i,j,times) 为投掷了 i次骰子,并且第 i个骰子的点数是 j,且这个 j的连续出现次数是 times的不同序列数量。
按照定义,最终返回的结果为 f(n,1,1)+f(n,1,2)+...f(n,1,rollMax[0])...f(n,2,1)+f(n,2,2)...+f(n,2,rollMax[1]+...f(n,6,rollMax[5])f(n,1,1) + f(n,1,2) + ...f(n,1,rollMax[0])...f(n,2,1)+f(n,2,2)...+f(n,2,rollMax[1] + ...f(n,6,rollMax[5])f(n,1,1)+f(n,1,2)+...f(n,1,rollMax[0])...f(n,2,1)+f(n,2,2)...+f(n,2,rollMax[1]+...f(n,6,rollMax[5])。
即 ∑j=16∑times=1rollMax[j−1]f(n,j,times)\sum_{j=1}^{6}\sum_{times=1}^{rollMax[j-1]}f(n,j,times)∑j=16∑times=1rollMax[j−1]f(n,j,times)。
状态转移:
- 当 当前点
k不等于 前一个点j时,f(i,k,1)=(f(i,k,1)+f(i−1,j,times))mod109+7f(i,k,1) = (f(i,k,1)+f(i-1,j,times)) mod 10^9+7f(i,k,1)=(f(i,k,1)+f(i−1,j,times))mod109+7 - 当 当前点
k等于 前一个点j并且times+1小于等于rollMax[j-1]时,f(i,j,times+1)=(f(i,j,times+1)+f(i−1,j,times))mod109+7f(i,j,times+1) = (f(i,j,times+1) + f(i-1,j,times)) mod 10^9+7f(i,j,times+1)=(f(i,j,times+1)+f(i−1,j,times))mod109+7
时间复杂度:O(n∗36∗15)O(n * 36 * 15)O(n∗36∗15)
C++代码:
const int MOD = 1e9+7;
using LL = long long;
class Solution {
public:int dieSimulator(int n, vector<int>& rollMax) {int f[n+1][7][16];memset(f,0,sizeof f);//初始化只投掷一次骰子的情况for(int i = 1;i <= 6;i++){f[1][i][1] = 1;}for(int i = 2;i <= n;i++){for(int j = 1;j <= 6;j++){for(int times = 1;times <= rollMax[j-1];times++){for(int k = 1;k <= 6;k++){if(j != k) f[i][k][1] = (f[i][k][1] + f[i-1][j][times])%MOD;else if(times + 1 <= rollMax[j - 1]){f[i][j][times+1] = (f[i][j][times+1] + f[i-1][j][times])%MOD;}}}}}LL ans = 0;//统计总的数量for(int j = 1;j <= 6;j++){for(int times = 1;times <= rollMax[j-1];times++) ans += f[n][j][times];}return ans % MOD;}
};
Java代码:
class Solution {private final int MOD = 1000_000_000+7;public int dieSimulator(int n, int[] rollMax) {int [][][] f = new int[n+1][7][16];for(int i = 1;i <= 6;i++){f[1][i][1] = 1;}for(int i = 2;i <= n;i++){for(int j = 1;j <= 6;j++){for(int times = 1;times <= rollMax[j-1];times++){for(int k = 1;k <= 6;k++){if(j != k) f[i][k][1] = (f[i][k][1] + f[i-1][j][times])%MOD;else if(times + 1 <= rollMax[j - 1]){f[i][j][times+1] = (f[i][j][times+1] + f[i-1][j][times])%MOD;}}}}}long ans = 0;for(int j = 1;j <= 6;j++){for(int times = 1;times <= rollMax[j-1];times++) ans += f[n][j][times];}return (int)(ans % MOD);}
}
相关文章:

Leetcode.1223 掷骰子模拟
题目链接 Leetcode.1223 掷骰子模拟 Rating : 2008 题目描述 有一个骰子模拟器会每次投掷的时候生成一个 1 到 6 的随机数。 不过我们在使用它时有个约束,就是使得投掷骰子时,连续 掷出数字 i 的次数不能超过 rollMax[i](i 从 1…...

数据分析到底该怎么学呢?讲真,真不难!
这几年,“数据分析”是很火啊,在这个数据驱动一切的时代,数据挖掘和数据分析就是这个时代的“淘金”,懂数据分析、拥有数据思维,往往成了大厂面试的加分项。 比如通过数据分析,我们可以更好地了解用户画像…...
活动星投票紫砂新青年制作一个投票活动
“紫砂新青年”网络评选投票_免费链接投票_作品投票通道_扫码投票怎样进行现在来说,公司、企业、学校更多的想借助短视频推广自己。通过微信投票小程序,网友们就可以通过手机拍视频上传视频参加活动,而短视频微信投票评选活动既可以给用户发挥…...
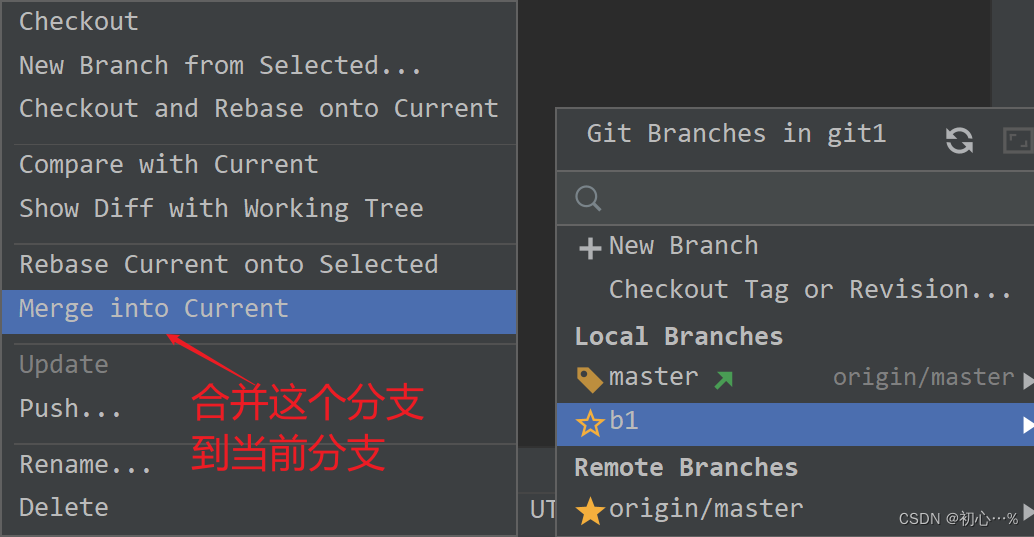
Git | 在IDEA中使用Git
目录 一、在IDEA中配置Git 1.1 配置Git 1.2 获取Git仓库 1.3 将本地项目推送到远程仓库 1.4 .gitignore文件的作用 二、本地仓库操作 2.1 将文件加入暂存区 2.2 将暂存区的文件提交到版本库 2.3 查看日志 三、远程仓库操作 3.1 查看和添加远程仓库 3.2 推送至远程仓…...
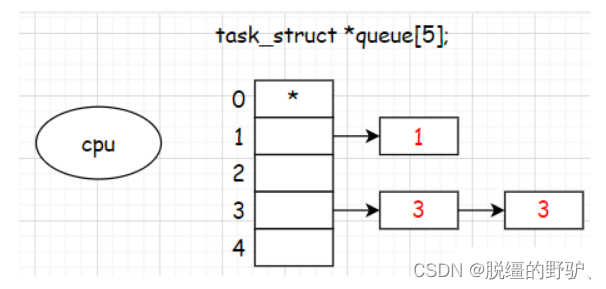
< Linux >:Linux 进程概念 (4)
目录 五、孤儿进程 六、进程优先级 6.1、基本概念 6.2、查看时实系统进程 6.3、PRI and NI 七、其他概念 四、X 状态:死亡状态 所谓进程处于 X 状态(死亡状态)代表的就是该进程已经死亡了,即操作系统可以随时回收它的资源(操作系统也可以…...
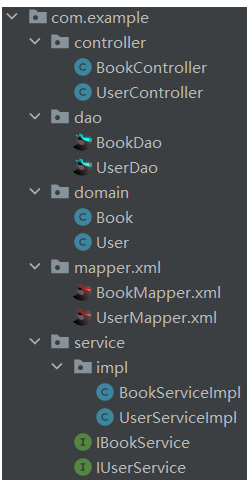
七、Java框架之MyBatisPlus
黑马课程 文章目录1. MyBatisPlus入门1.1 MyBatisPlus入门案例步骤1:创建spring boot工程步骤2:配置application.yml步骤3:创建数据库表(重点)步骤4:编写dao层步骤5:测试1.2 标准数据层开发标准…...

C语言柔性数组
目录什么是柔性数组柔性数组的使用什么是柔性数组 柔性数组是在C99中定义的 结构体的最后一个元素允许是未知大小的数组,这就叫柔性书组 柔性数组的长度可以写成0,也可以不规定数组长度 下面两种写法都是正确的 struct S { int i; int a[0];//柔性数…...

支付功能测试用例
Author:ChatGPT用例设计下面是一些支付功能测试用例:账户余额检查:测试用户的账户余额是否准确。支付方式选择:测试用户可以使用的支付方式,包括信用卡、借记卡、电子钱包等。支付金额确认:测试用户输入的支…...
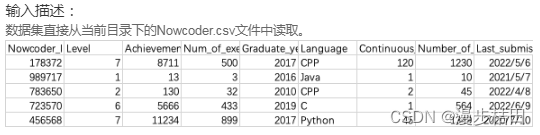
牛客网Python篇数据分析习题(一)
1.现有一个Nowcoder.csv文件,它记录了牛客网的部分用户数据,包含如下字段(字段与字段之间以逗号间隔): Nowcoder_ID:用户ID Level:等级 Achievement_value:成就值 Num_of_exercise&a…...

【C语言】“指针类型”与“野指针”
文章目录一、指针是什么❔二、指针和指针类型1.指针-整数2.指针解引用三.野指针1.引起野指针的原因2.如果避免野指针完结一、指针是什么❔ 指针也就是 内存地址 ,在计算机上我们访问数据需要通过内存地址来访问,在C语言中,指针变量是用来存放…...

Linux:软链接和硬链接的理解
Linux通过命令行创建快捷方式使用的命令是ln,这里就涉及到了软链接和硬链接,确实有些不好理解,如果你也一样,那么可以继续看下去了 目录ln命令语法实操创建软链接:ln -s [源文件或目录][目标文件或目录]创建硬链接&…...

力扣HOT100 (1-5)
目录 1.两数之和 2.两数相加 拓展到牛客的TOP101的BM11( 链表相加(二)) 3.无重复的最长子串(牛客BM92) 解法1: 解法2: 4.寻找两个正序数组的中位数 5.最长回文子串 1.两数之和 思路:用Has…...

车载基础软件——AUTOSAR CP典型应用案例SOME/IP和TSN时间同步
我是穿拖鞋的汉子,魔都中坚持长期主义的一个屌丝工程师! 今天是2023年2月7日,上海还在下着雨,估计是到了梅雨时节(提前到来?),真想说句我劝天公重安排,不让梅雨早时来!!! 老规矩分享一段喜欢的文字,避免自己成为高知识低文化的工科男: “ 我们只需做的,是走好…...
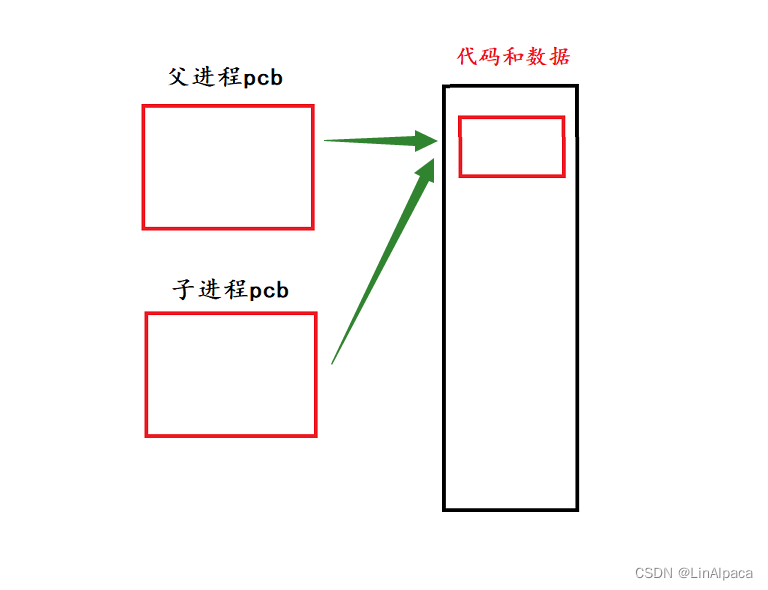
【Linux】操作系统与进程的概念
目录 冯诺依曼体系 注意 为什么CPU不直接访问输入或输出设备? 跨主机间数据的传递 操作系统 管理 进程 描述进程 进程的查看和终止 bash 通过系统调用创建子进程 fork的辨析 冯诺依曼体系 🥖冯诺依曼结构也称普林斯顿结构,是一种将…...

(1分钟突击面试) 高斯牛顿、LM、Dogleg后端优化算法
高斯牛顿法 LM法 DogLeg方法编辑切换为居中添加图片注释,不超过 140 字(可选)知识点:高斯牛顿是线搜索方法 LM方法是信赖域方法。编辑切换为居中添加图片注释,不超过 140 字(可选)这个就是JTJ是…...

d3.js与echarts对比
D3.js 和 ECharts 是两种常用的数据可视化工具,它们有着不同的优缺点: D3.js: 优点: 功能强大,提供了极高的灵活性和定制性,支持多种图表类型,如柱状图、饼图、散点图、树图、网络图等。 可以…...
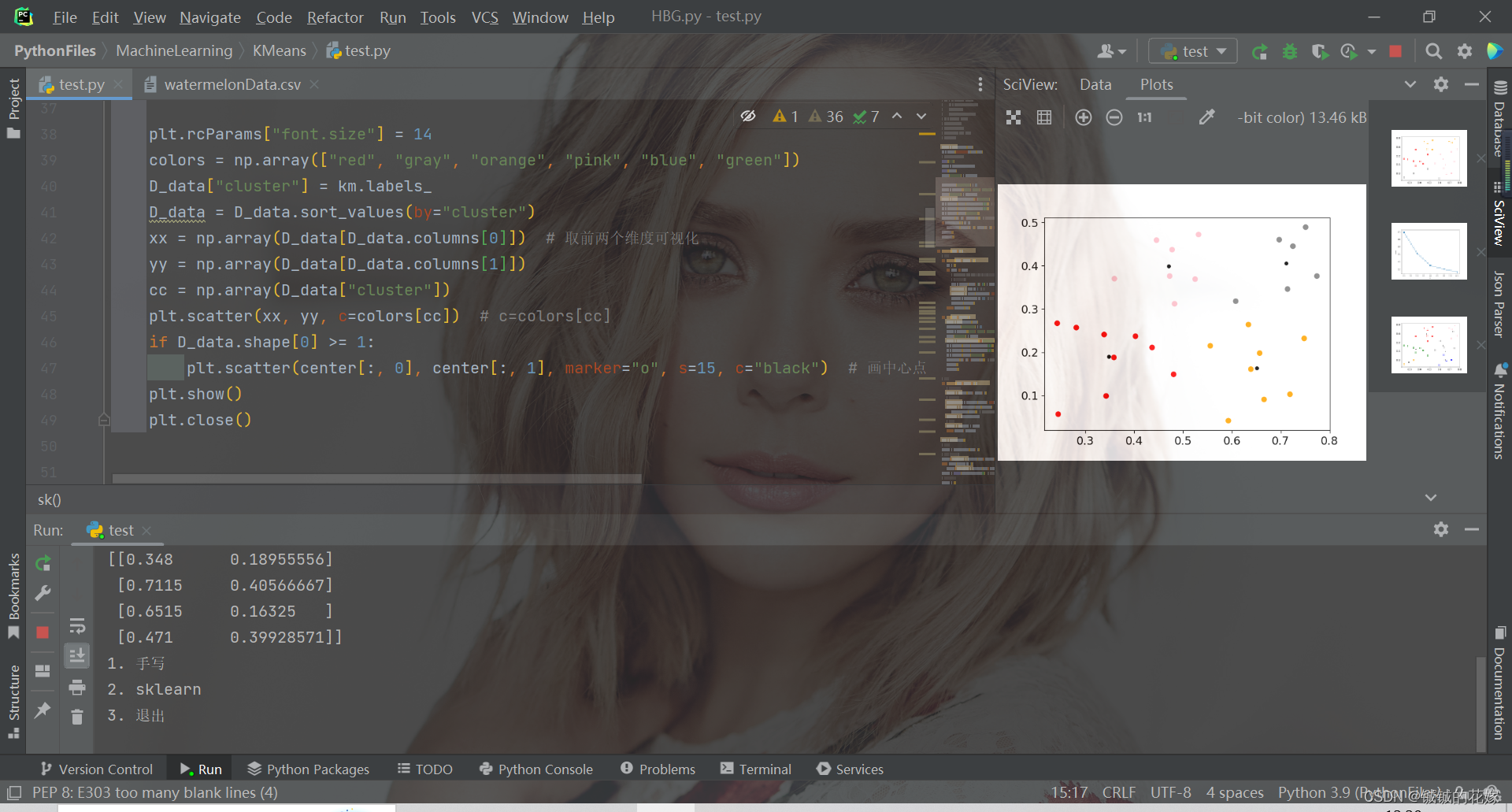
机器学习之K-means原理详解、公式推导、简单实例(python实现,sklearn调包)
目录1. 聚类原理1.1. 无监督与聚类1.2. K均值算法2. 公式推导2.1. 距离2.2. 最小平方误差3. 实例3.1. python实现3.2. sklearn实现4. 运行(可直接食用)1. 聚类原理 1.1. 无监督与聚类 在这部分我今天主要介绍K均值聚类算法,在这之前我想提一…...

OBS 进阶 一个从自定义对话框中 传参到插件的例子
目录 一、自定义对话框,传参综合例子 1、自定义对话框 1)自定义对话框类...
在Linux和Windows上编译datax-web-ui源码
记录:375场景:在CentOS 7.9操作系统上,使用apache-maven-3.8.7安装编译datax-web-ui源码。在Windows上操作系统上,使用apache-maven-3.8.7编译datax-web-ui源码。版本:JDK 1.8 node-v14.17.3 npm-6.14.13datax-web-ui开…...

React组件生命周期管理
组件生命,就是组件在不同阶段提供对应的钩子函数,来处理逻辑操作。比如初始化阶段,我们需要初始化组件相关的状态和变量。组件销毁阶段时,我们需要把一些数据结构销毁来节约内存。 React组件生命周期 React组件生命周期分为三个阶段:挂载阶段【Mount】、更新阶段【Updat…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
