【面试HOT200】回溯篇
系列综述:
💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。
🥰来源:材料主要源于【CodeTopHot300】进行的,每个知识点的修正和深入主要参考各平台大佬的文章,其中也可能含有少量的个人实验自证,所有代码均优先参考最佳性能。
🤭结语:如果有帮到你的地方,就点个赞和关注一下呗,谢谢🎈🎄🌷!!!
🌈【C++】秋招&实习面经汇总篇
文章目录
- 基础知识
- 回溯基础算法模板
- 组合问题
- 无重复元素的组合
- 有重复元素的组合
- 排列问题
- 无重复元素的全排列
- 有重复元素的全排列
- HOT200回溯相关题目
- 39. 组合总和
- 40. 组合总和 II
- 93. 复原 IP 地址
- 131. 分割回文串
- 1005. K 次取反后最大化的数组和
- 参考博客
😊点此到文末惊喜↩︎
基础知识
- 回溯算法 = 穷举 + 剪枝
- 穷举:从
一个选择开始,一步步尝试每一个可能的选择,如果某次选择导致问题无法解决,则回溯并选择另一种可能,直到找到一个可行的解或者穷举所有可能的解。 - 剪枝:在搜索过程中,根据问题的限制条件,减少搜索空间,提高算法效率
- 穷举:从
- 作用
- 在多个选择中搜索出
满足条件的所有可能解 - 一般地,组合问题和排列问题是在树形结构的叶子节点上收集结果,而子集问题就是取树上所有节点的结果。
- 在多个选择中搜索出
- 回溯算法解决的问题一般为npc问题,难以使用常规算法进行解决
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则选出M个,有几种排列方式
- 棋盘问题:N皇后,解数独等等
- 组合问题:N个数里面按一定规则找出k个数的集合
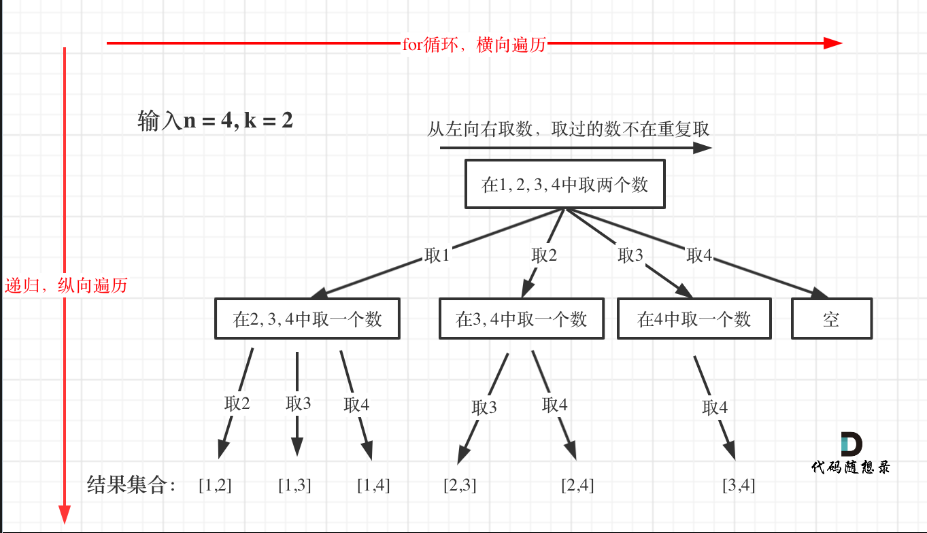
- 所有的回溯法解决的问题都可以抽象为树形结构
- 根节点是总数据集合,树枝节点是可选数据集合
- 叶子节点为根节点到叶子节点的路径的选择集合
// 结果集和路径集
vector<vector<type> res;
vector<type> path;
void backtracking(vecotr<type> candidates, int startIndex) {// 针对当前选择的合法性判断auto is_ok = [](const type &data)->bool{// type中数据项的合法性判断};// 递归出口:结点剪枝,生成慢if (is_ok(val)) {res.push_back(path);return;}// 延申和回撤路径时,可能涉及多个状态标记变量的改动for (int i = startIndex; i < candidates.size(); ++i) {分叉剪枝判断(性能高);// 状态延申改动path.push_back(candidates[i]);// 向下延申backtracking(剩余可选列表); // 回溯// 状态回撤改动path.pop_back();// 回撤延申}
}
// 主函数
vector<vector<int>> combine(vector<type>& candidates) {res.clear(); // 可以不写path.clear();// 可以不写backtracking(candidates, 0);return result;}
回溯基础算法模板
模板使用的初衷:将问题的输入转换成对应模板的输入格式,然后调用模板的函数(已经背诵的)进行快速的求解
组合问题
- 组合问题的复杂度
- 时间复杂度: O ( C n k × k ) O(C_n^k × k) O(Cnk×k),总共有 C n k C_n^k Cnk种组合,每种组合需要 O ( k ) O(k) O(k) 的时间复杂度
- 空间复杂度: O ( n ) O(n) O(n),递归深度为n,所以系统栈所用空间为 O ( n ) O(n) O(n)
无重复元素的组合
- 基本概述
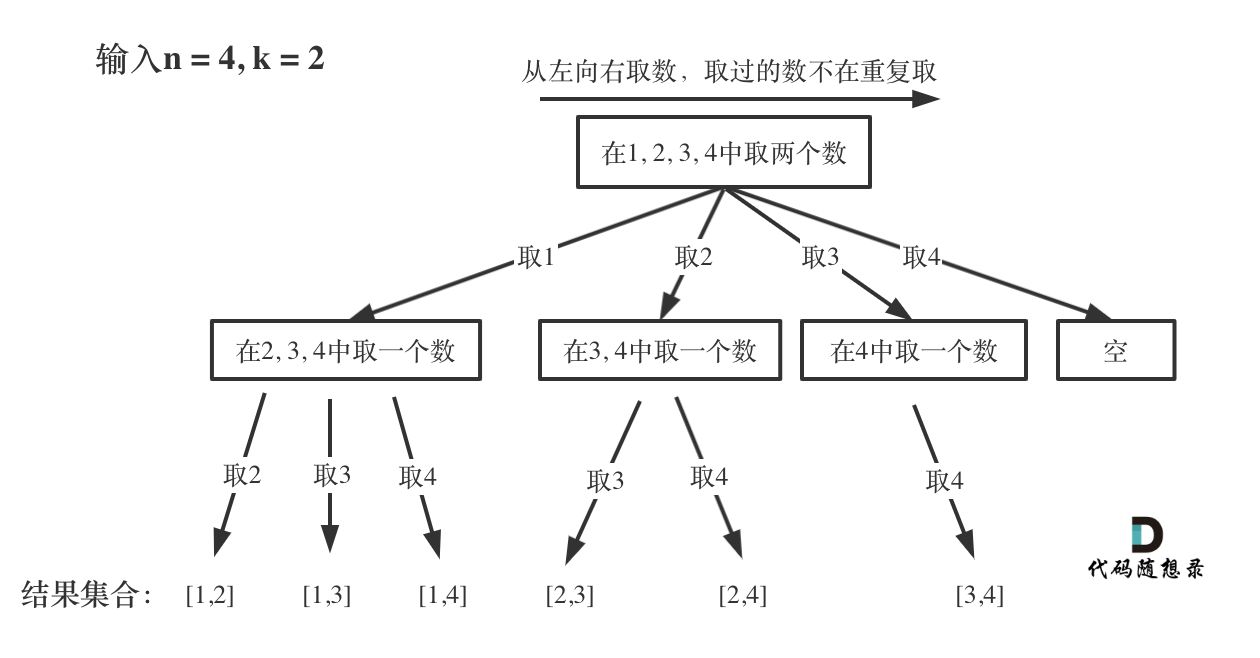
- 问题:从
无重复元素的集合中选出K个元素组成组合,每个元素只能被选取一次,且选出的元素之间没有顺序之分。 - 举例:从元素集合{1,2,3}中选择2个元素的组合为{(1,2),(1,3),(2,3)}。
- 问题:从
- 代码
- 解决的问题:给定一个
线性表,求该线性表中满足条件的组合 - 示例:求线性表中所有个数为target的结果。
- 剪枝:列表中剩余元素
(vec.size() - i) >= 所需需要的元素个数(target - path.size())
- 解决的问题:给定一个
// 从候选集candidate中选出任意k个数组成的集合
vector<vector<int>> Backtracking(vector<int> &candidate, int k) {const int len = candidate.size();// 递归函数vector<int> path; // 符合条件的路径vector<vector<int>> res; // 符合条件的路径集合auto self = [&](auto &&self, int pos){// 递归出口:满足条件的路径加入结果集中if (path.size() == k) {res.push_back(path);return;}// i = start表示从之后剩余中选择for (int i = pos; i < len ; ++i) {if (i > len - (k-path.size())) continue;path.push_back(candidate[i]); // 做出选择self(self, i+1);// key: 是i+1 // 递归path.pop_back(); // 撤销选择}};self(self, 0);return res;
}有重复元素的组合
- 基本概述
- 问题:从
有重复元素的组合中选出若干元素组成组合,每个元素只能被选取一次,且选出的元素之间没有顺序之分。 - 举例:从集合{1, 2, 2, 3}中选择2个元素的组合为{1, 2}、{1, 3}、{2, 2}、{2, 3}。
- 问题:从
- 代码
- 解决问题:给定一个
线性表,求该线性表中满足条件的组合,因为有重复元素,所以选择重复元素时只能使用一次,否则会出现集合中的重复
- 解决问题:给定一个
vector<vector<int>> Backtracking(vector<int> &candidate, int k) {// 排序sort(candidate.begin(), candidate.end());// 递归匿名函数vector<int> path;vector<vector<int>> res;auto self = [&](auto &&self, int pos){if (path.size() == k) {res.push_back(path);return;}for (int i = pos; i < candidate.size(); ++i) {// key: i > pos。第一次选取到重复的数,不会影响后面if (i > pos && candidate[i] == candidate[i-1])continue;path.push_back(candidate[i]);self(self, i+1);path.pop_back();}};// 递归调用self(self, 0);return res;
}
排列问题
- 组合问题的复杂度
- 时间复杂度: O ( n × n ! ) O(n×n!) O(n×n!),一共 n ! n! n! 种组合,每种排列构造时间需要 O ( n ) O(n) O(n) 的时间复杂度
- 空间复杂度: O ( n ) O(n) O(n),递归深度为n,所以系统栈所用空间为 O ( n ) O(n) O(n)
无重复元素的全排列
- 基本概述
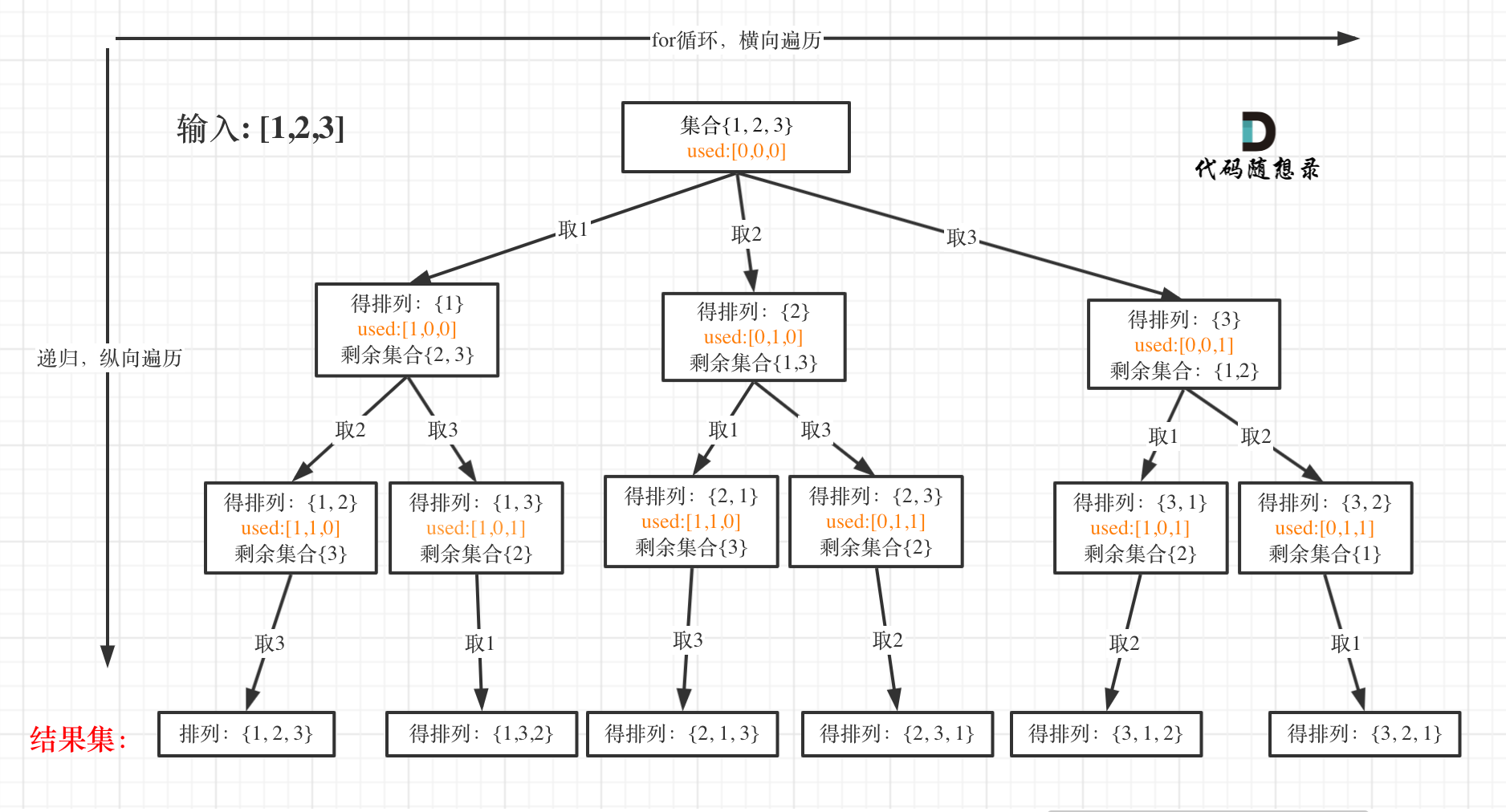
- 问题:无重复元素的排列是指在
给定一组不同的元素中,按照一定的顺序排列出所有可能的组合,每个元素只出现一次。 - 举例:从集合{1, 2, 3},则可以产生以下6种无重复元素的排列:{1, 2, 3}、{1, 3, 2}、{2, 1, 3}、{2, 3, 1}、{3, 1, 2}、{3, 2, 1}。
- 问题:无重复元素的排列是指在
- 代码
- 不需要使用pos,每一个i对应一位
vector<vector<int>> permute(vector<int>& candidate) {const int len = candidate.size();vector<int> path; // 回溯路径vector<vector<int>> res; // 回溯结果集vector<bool> used(len, false); // 使用标记auto self = [&](auto &&self){ // 回溯算法if (path.size() == len) {res.push_back(path);return ;}for (int i = 0; i < len; ++i) {// path里已经收录的元素,直接跳过if (used[i] == true) continue;// 增加选择used[i] = true;path.push_back(candidate[i]);// 进行回溯self(self);// 撤回选择used[i] = false;path.pop_back();}};// 调用self(self);return res; }
有重复元素的全排列
-
基本概述
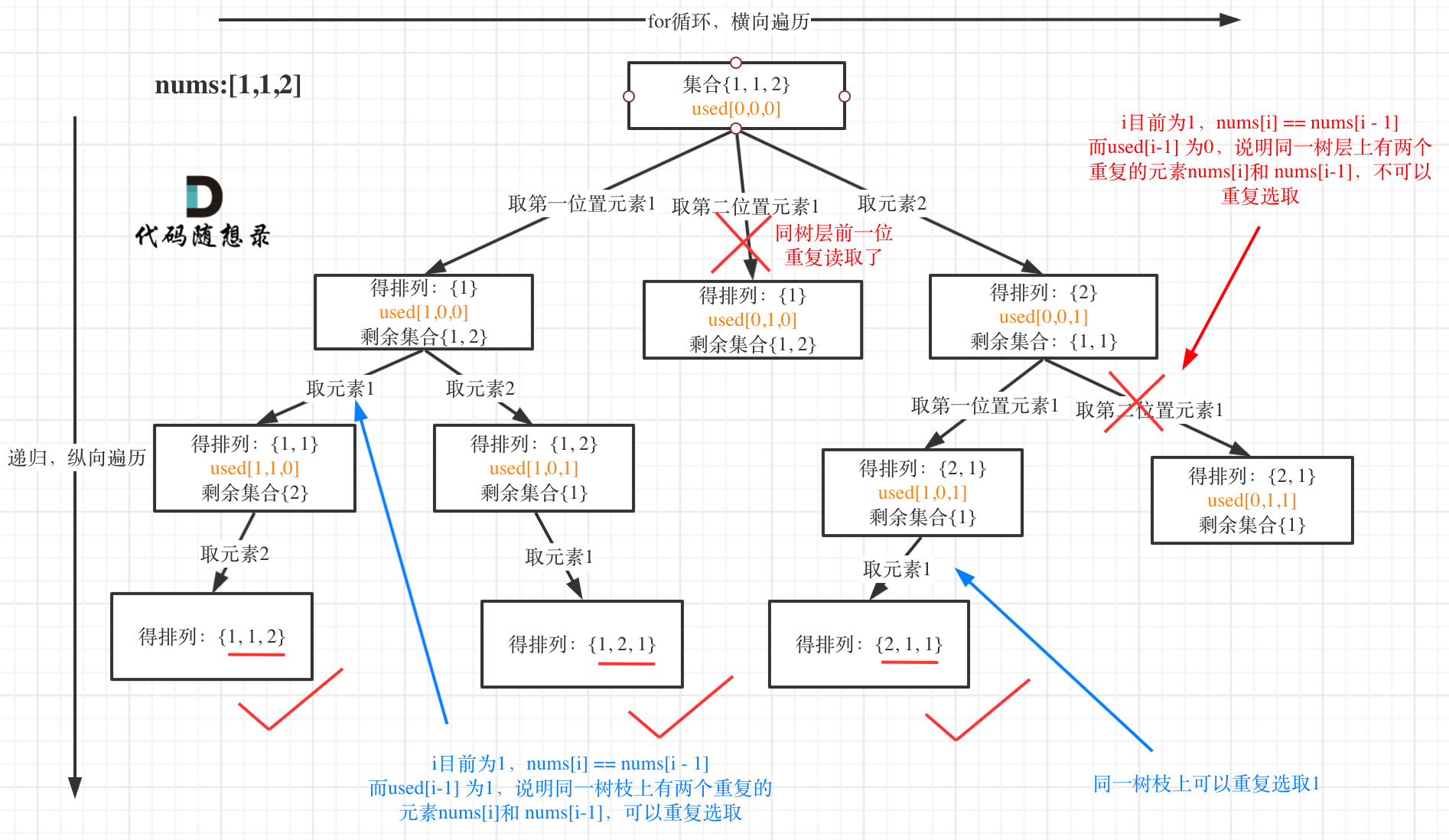
- 问题:无重复元素的排列是指在
给定一组不同的元素中,按照一定的顺序排列出所有的不重复组合 - 举例:从集合[1,1,2],则可以产生无重复的全排列: [1,1,2], [1,2,1], [2,1,1]
- 问题:无重复元素的排列是指在
-
代码
- 产生重复解的原因:例如[1,1,2], 无法区分[1(0), 1(1), 2] 和[1(1), 1(0), 2] 这两种情况的解
vector<vector<int>> permuteUnique(vector<int>& candidate) {const int len = candidate.size();sort(candidate.begin(), candidate.end());// 递归vector<int> path;vector<vector<int>> res;vector<bool> used(len, false); // key:注意初始化auto self = [&](auto &&self){if (path.size() == len) {res.emplace_back(path);return ;}for (int i = 0; i < len; ++i) {// 有效的重复元素 && 前一个元素未被使用// 保证相同元素同层中只有第一个被使用if (i > 0 && candidate[i] == candidate[i-1] && used[i-1] == false) continue;if (used[i] == false) {used[i] = true;path.emplace_back(candidate[i]);self(self);used[i] = false;path.pop_back();}}};self(self);return res; }// 哈希表处理重复解 vector<vector<int>> permuteUnique(vector<int>& candidate) {const int len = candidate.size();// 去重unordered_map<int, int> umap;for (auto &i : candidate) ++umap[i];// 回溯算法vector<vector<int> > res;vector<int> path;auto self = [&](auto &&self, int pos){// 递归出口if (pos == len) {res.push_back(path);return ;}for (auto &i : umap) {if (i.second == 0) continue;path.push_back(i.first);--i.second;self(self, pos+1);path.pop_back();++i.second;}};self(self, 0);return res; } - 产生重复解的原因:例如[1,1,2], 无法区分[1(0), 1(1), 2] 和[1(1), 1(0), 2] 这两种情况的解
HOT200回溯相关题目
39. 组合总和
- 题目
- 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回
- candidates 中的 同一个 数字可以 无限制重复被选取
- 输入:candidates = [2,3,5], target = 4
- 输出:[[2,2]]
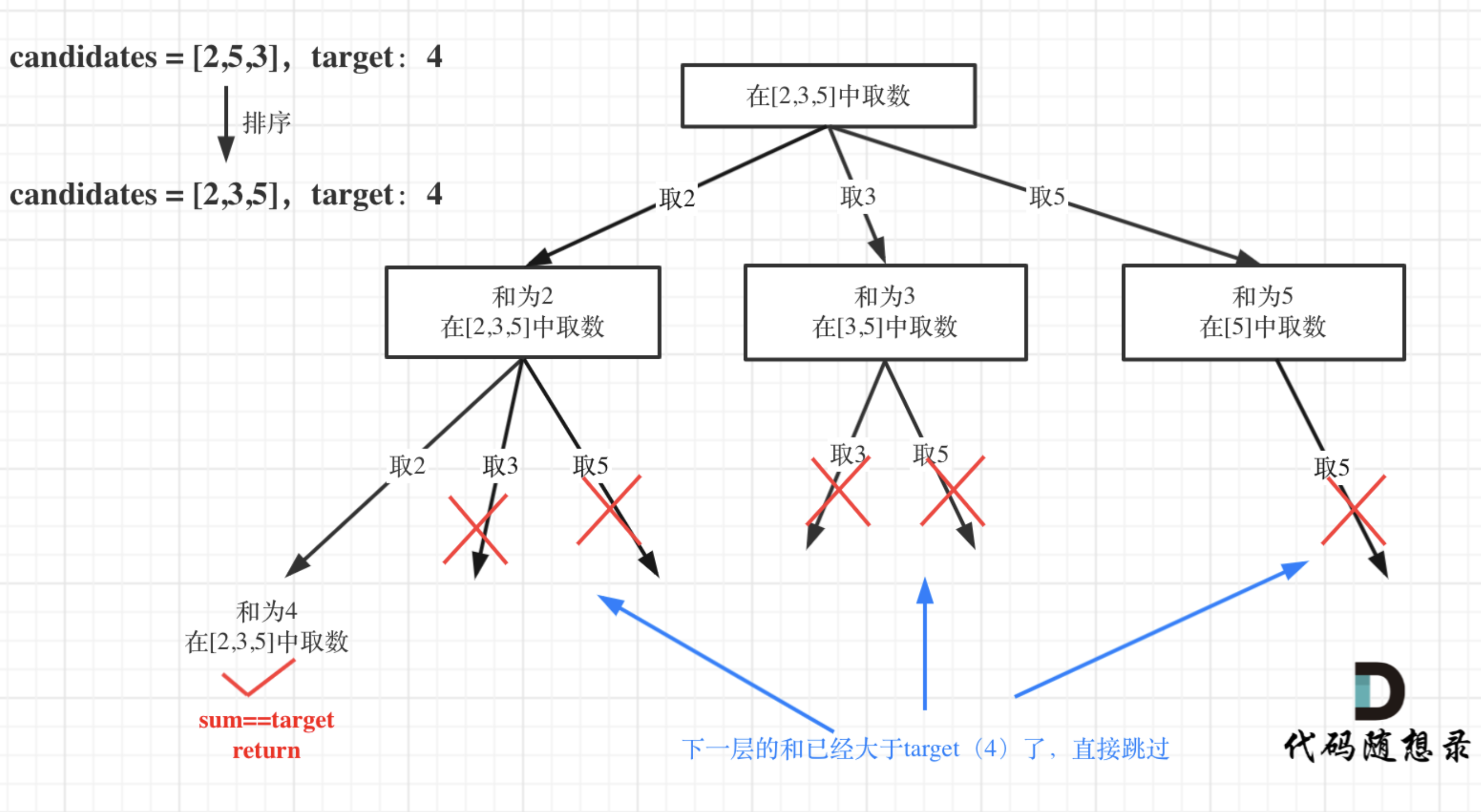
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {vector<vector<int>> res;vector<int> path;auto self = [&](auto &&self, int pos, int sum){// 结束条件if (sum > target) return ;if (sum == target) {res.push_back(path);return ;}// 路径回溯for (int i = pos; i < candidates.size(); ++i) {sum += candidates[i];path.push_back(candidates[i]);self(self, i, sum); // key: 不用i+1表示可重复读取当前值sum -= candidates[i];path.pop_back();}};self(self, 0, 0);return res;
}
40. 组合总和 II
- 题目
- 给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
- 输入: candidates = [2,5,2,1,2], target = 5,
- 输出:[ [1,2,2], [5] ]
- 代码
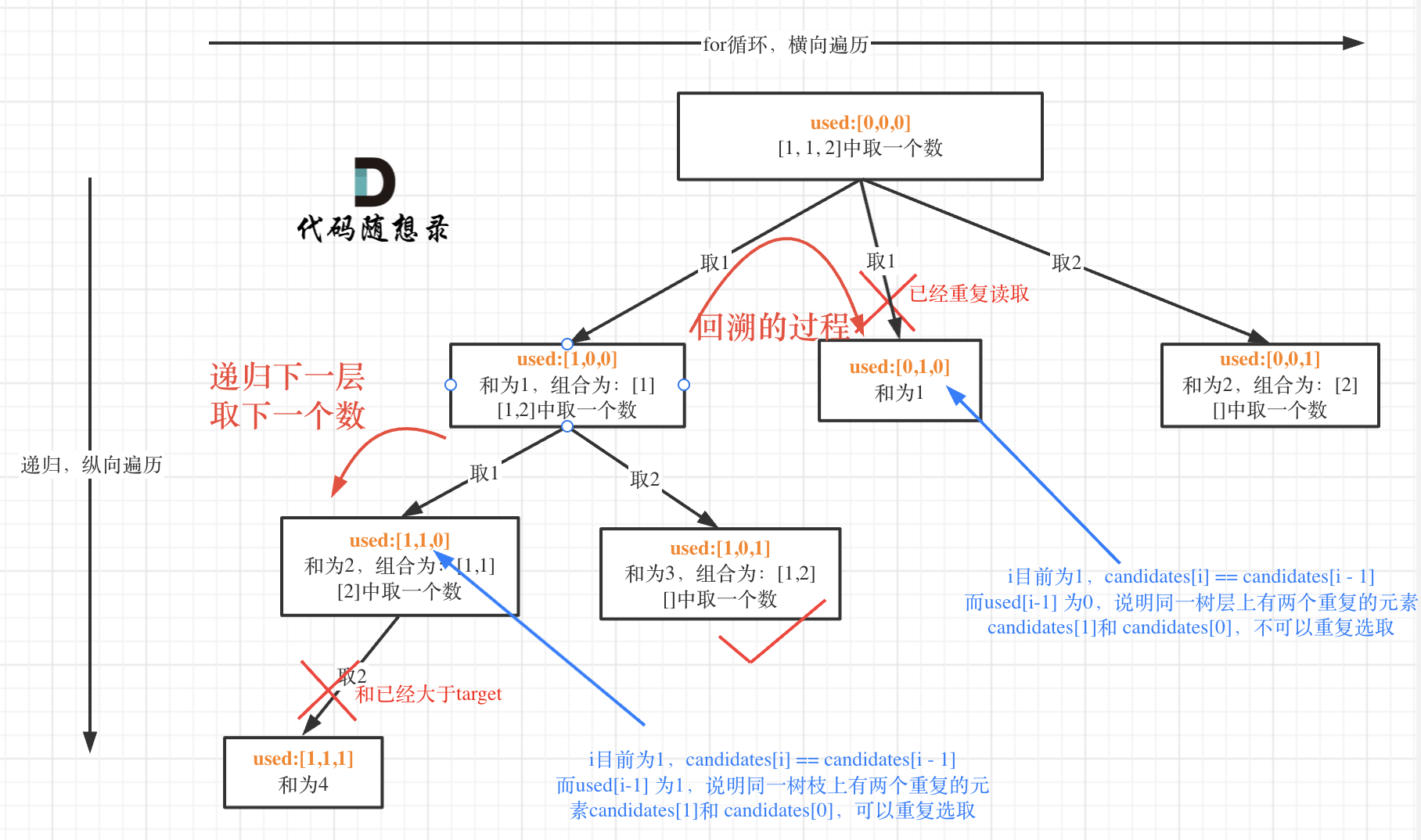
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {const int len = candidates.size();sort(candidates.begin(), candidates.end());// 回溯部分vector<int> path;vector<vector<int>> res;vector<bool> used(len, false);int sum = 0;auto self = [&](auto &&self, int pos){// 结点剪枝if (sum == target) {res.emplace_back(path);return ;}for (int i = pos; i < len; ++i) {// 分叉剪枝: 性能高一些if (sum + candidates[i] > target) continue;if (i > 0 && candidates[i] == candidates[i-1] && used[i-1] == false) continue;if (used[i] == true) continue;used[i] = true;path.emplace_back(candidates[i]);sum += candidates[i];self(self, i+1); // i+1表示每个元素不重复使用sum -= candidates[i];path.pop_back();used[i] = false;}};self(self, 0);return res;
}
93. 复原 IP 地址
- 题目
- 给定一个只包含数字的字符串 s ,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在 s 中插入 ‘.’ 来形成
- 输入:s = “25525511135”
- 输出:[“255.255.11.135”,“255.255.111.35”]
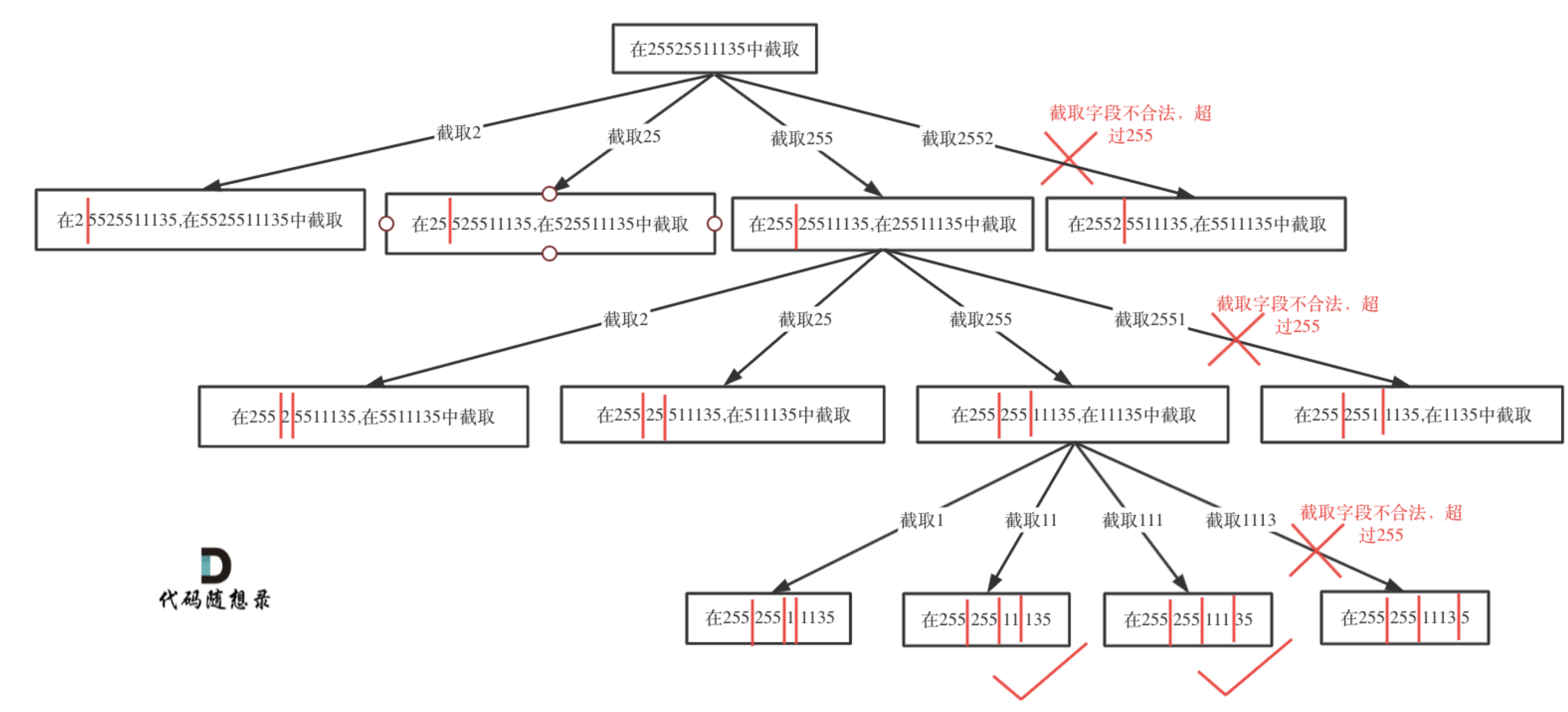
vector<string> restoreIpAddresses(string s) {const int len = s.size();// 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法auto is_valid = [](const string& s, int start, int end) {cout << start <<' ' << end << endl;if (start > end) {return false;}if (s[start] == '0' && start != end) // 0开头的数字不合法return false;int num = 0;for (int i = start; i <= end; i++) {if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法return false;}num = num * 10 + (s[i] - '0');if (num > 255) { // 如果大于255了不合法return false;}}return true;
};
131. 分割回文串
- 131. 分割回文串
- 获取
[startIndex,i]在s中的子串s.substr(startIndex, i - startIndex + 1)
// 判断是否为回文字符串 bool isPalindrome(const string& s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s[i] != s[j]) {return false;}}return true; } // 基本的回溯 vector<vector<string>> result; vector<string> path; // 放已经回文的子串 void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}for (int i = startIndex; i < s.size(); i++) {// 剪枝与枝的延长if (isPalindrome(s, startIndex, i)) { // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else { // 不是回文,跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back(); // 回溯过程,弹出本次已经填在的子串} }vector<vector<string>> partition(string s) {result.clear();path.clear();backtracking(s, 0);return result; } - 获取
1005. K 次取反后最大化的数组和
- 1005. K 次取反后最大化的数组和
- sort的使用:第三个参数为自定义的排序队则,在头文件#include
- accumulate的使用:第三个参数为累加的初值,在头文件include
static bool cmp(int a, int b) {return abs(a) > abs(b);// 绝对值的从大到小进行排序 } int largestSumAfterKNegations(vector<int>& A, int K) {// 将容器内的元素按照绝对值从大到小进行排序sort(A.begin(), A.end(), cmp); // 在K>0的情况下,将负值按照绝对值从大到小依次取反for (int i = 0; i < A.size(); i++) { if (A[i] < 0 && K > 0) {A[i] *= -1;K--;}}// 如果K为奇数,将最小的正数取反if (K % 2 == 1) A[A.size() - 1] *= -1; // 求和return accumulate(A.begin(),A.end(),0);// 第三个参数为累加的初值,在头文件include<numeric> }
🚩点此跳转到首行↩︎
参考博客
- 「代码随想录」47. 全排列 II:【彻底理解排列中的去重问题】详解
- codetop
相关文章:

【面试HOT200】回溯篇
系列综述: 💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于【CodeTopHot300】进行的,每个知识点的修正和深入主要参…...

JVM——内存溢出和内存泄漏
目录 1. 内存溢出和内存泄漏内存泄漏的常见场景解决内存溢出的思路1.发现问题 – Top命令2.发现问题 – VisualVM3.发现问题 – Arthas4.发现问题 – Prometheus Grafana5.发现问题 – 堆内存状况的对比
《凤凰项目》读书笔记
文章目录 一、书名和作者二、书籍概览2.1 主要论点和结构2.2 目标读者和应用场景 三、核心观点与主题3.1 DevOps的核心原则与文化变革3.2 持续交付与自动化3.3 变更管理与风险控制3.4 关键绩效指标与持续改进 四、亮点与启发4.1 最有影响的观点4.2 对个人专业发展的启示 五、批…...

熬夜会秃头——beta冲刺Day4
这个作业属于哪个课程2301-计算机学院-软件工程社区-CSDN社区云这个作业要求在哪里团队作业—beta冲刺事后诸葛亮-CSDN社区这个作业的目标记录beta冲刺Day4团队名称熬夜会秃头团队置顶集合随笔链接熬夜会秃头——Beta冲刺置顶随笔-CSDN社区 一、团队成员会议总结 1、成员工作进…...

HTML5+CSS3+Vue小实例:浪漫的心形文字动画特效
实例:浪漫的心形文字动画特效 技术栈:HTML+CSS+Vue 效果: 源码: 【HTML】 <!DOCTYPE html> <html><head><meta http-equiv="content-type" content="text/html; charset=utf-8"><meta name="viewport" conte…...

数据结构-基数排序
基数排序 基本思想 基数排序其实就是依靠多位关键字进行排序,现在我们有一个数据为101,那么“101”就是一个三位 关键字,分别为:“百位->1”、“十位->0”、“个位->1”。 此时我们就可以按照三位关键字进行排序&…...
基于ASP.NET MVC技术的图书管理系统的设计与实现
基于ASP.NET MVC技术的图书管理系统的设计与实现 摘要:图书管理系统是一套高新科学技术和图书知识信息以及传统历史文化完美结合的体现。它改变了传统图书收藏的静态书本式图书服务特征,实现了多媒体存取、远程网络传输、智能化检索、跨库无缝链接、创造…...
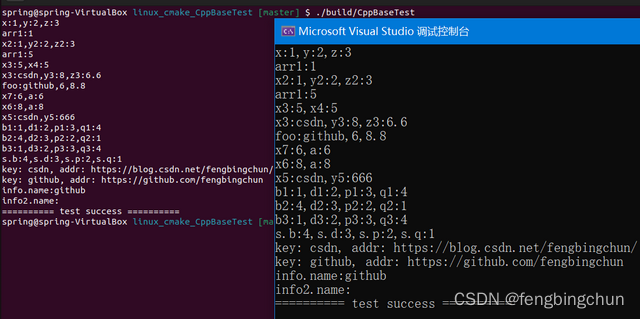
C++17中的结构化绑定
C17中的结构化绑定(structured binding):将指定名称绑定到初始化程序的子对象或元素。简而言之,它们使我们能够从元组或结构中声明多个变量。与引用一样,结构化绑定是现有对象的别名;与引用不同,结构化绑定不必是引用类型(referen…...
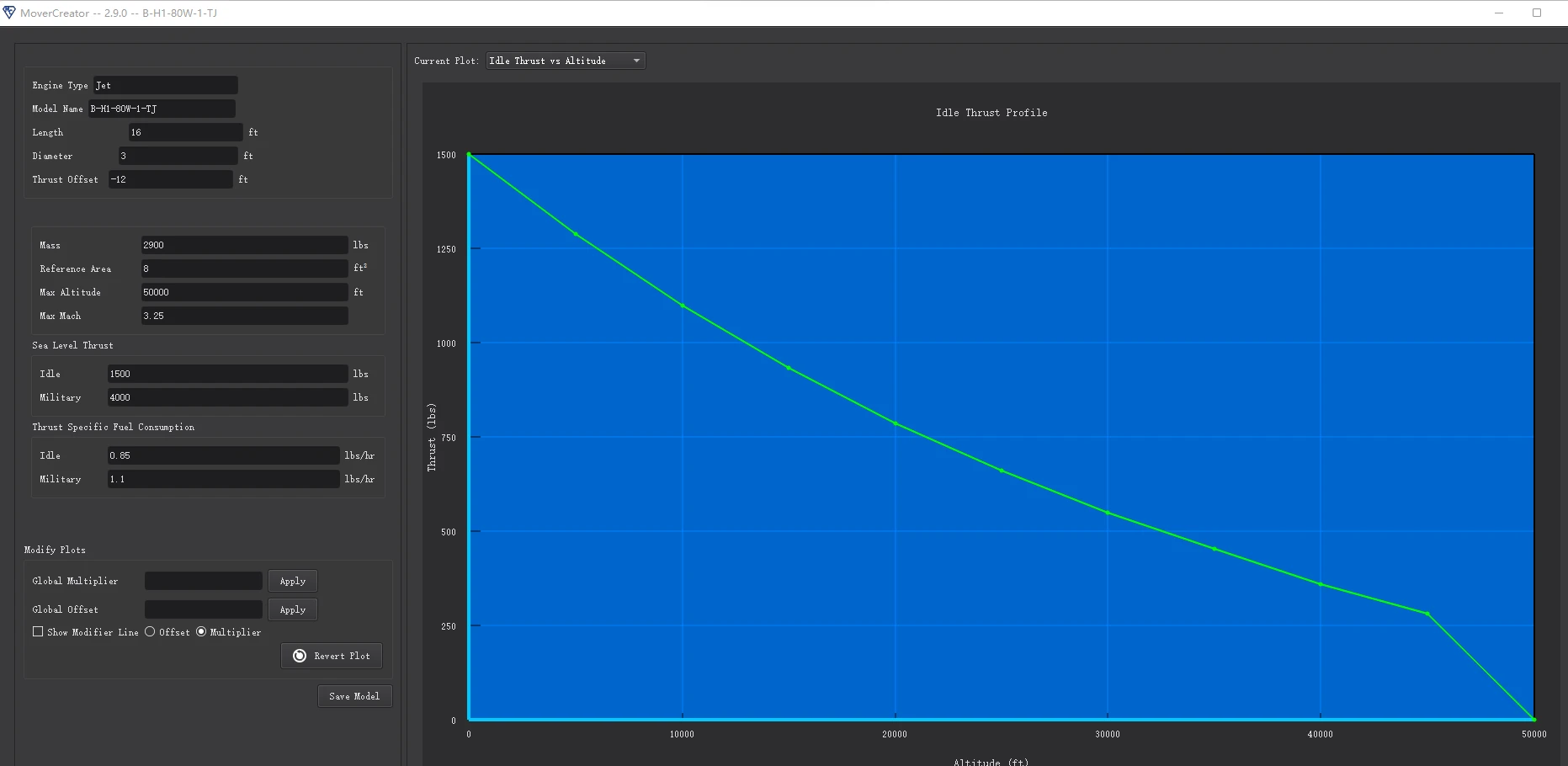
Mover Creator 用户界面
1 “开始”对话框 首次打开 Mover Creator 时,出现的第一个页面是“开始”对话框,如下所示。从这里开始,用户可以选择开始设计飞机、武器或发动机。在上述每种情况下,用户都可以创建新模型或编辑现有模型。 1.1 新建模型 如果用…...

『Nginx安全访问控制』利用Nginx实现账号密码认证登录的最佳实践
📣读完这篇文章里你能收获到 如何创建用户账号和密码文件,并生成加密密码配置Nginx的认证模块,实现基于账号密码的登录验证 文章目录 一、创建账号密码文件1. 安装htpasswd工具1.1 CentOS1.2 Ubuntu 二、配置Nginx三、重启Nginx 在Web应用程…...

MongoDB导入导出命令
(1)mongoexport命令 例如: mongoexport --db testdb --collection person --out person.json mongoexport --db testdb --collection person --fields name,age --out person.json mongoexport --db testdb --collection person --query {&qu…...
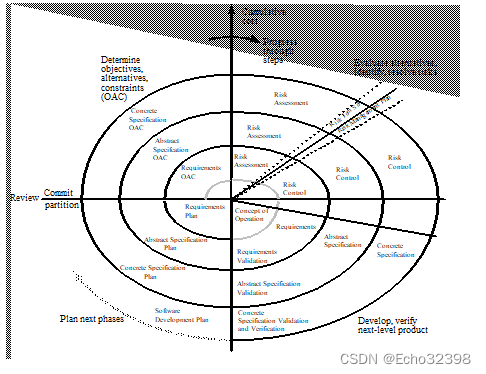
软件工程期末复习(1)
学习资料 软件工程知识点总结_嘤桃子的博客-CSDN博客 软件工程学习笔记_软件工程导论第六版张海藩pdf-CSDN博客 【软件工程】软件工程期末试卷习题课讲解!!_哔哩哔哩_bilibili 【拯救者】软件工程速成(期末考研复试软考)均适用. 支持4K_哔哩哔哩_bil…...

nextjs入门
创建项目 npx create-next-app 项目名 体验文件路由 nextjs提供了文件路由的功能, 根据文件系统的目录结构, 可以识别为对应的页面路由 创建页面 首先, 在src下创建pages目录, 然后创建一个about文件(对应about页面)和main/index.js文件(对应首页) pages/main/index con…...

【C语言】字符串函数strlen #strcpy #strcmp #strcat #strstr及其模拟实现
在C语言中,有一种特殊的数据类型,即字符串类型。C 并没有专门定义一个字符串类型,这对我们使用字符串造成了一定的麻烦。但是,C标准库<string.h> 中定义了各种字符串函数,这对于我们来说是一件值得庆幸的事情。…...

递归实现组合型枚举
递归实现组合型枚举 #include<iostream> #include<vector>int n, m; std::vector<int>res; bool st[30];void Print() {for(int i0;i<res.size();i){printf("%d ",res[i]);}puts(""); }void dfs(int num) {if (res.size() m){Print(…...

SCAU:1065 数组中的指针
1065 数组中的指针 时间限制:1000MS 代码长度限制:10KB 提交次数:3436 通过次数:1692 题型: 编程题 语言: G;GCC Description 设有如下数组定义: int a[3][4]{{1,3,5,7},{9,11,13,15},{17,19,21,23}}; 计算下面各项的值(设数组a的首地址为2000&…...

找不到msvcp110.dll如何修复?分享5个亲测有效的修复方法
在计算机使用过程中,我们经常会遇到一些错误提示,其中之一就是“msvcp110.dll丢失”。这个错误通常发生在运行某些程序时,系统无法找到所需的动态链接库文件。那么,msvcp110.dll到底是什么呢?它又有什么作用࿱…...

LeetCode刷题笔记第80题:删除有序数组中的重复项 II
LeetCode刷题笔记第80题:删除有序数组中的重复项 II 题目: 删除升序数组中超过两次的元素后的数组长度 想法: 使用快慢指针的方法完成,使用快指针遍历整个数组,使用慢指针完成相同元素最多保留两个。在快指针遍历到…...

【开源存储】minio对象存储部署实践
文章目录 一、前言1、介绍说明2、部署方式3、冗余模式4、约束限制4.1、规格参数4.2、API支持a、minio不支持的Amazon S3 Bucket APIb、minio不支持的Amazon S3 Object API 二、部署说明1、软件安装2、minio单机部署3、minio分布式部署3.1、前置条件3.2、开始运行3.3、操作说明 …...
)
Java编程强化练习(二)
表达式计算(支持空格,连乘,连除)(选做题,不计分) 【问题描述】 从标准输入中读入一个整数算术运算表达式,如5 - 1 * 2 * 3 12 / 2 / 2 。计算表达式结果,并输出。 …...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...
