递归实现组合型枚举
递归实现组合型枚举

#include<iostream>
#include<vector>int n, m;
std::vector<int>res;
bool st[30];void Print()
{for(int i=0;i<res.size();i++){printf("%d ",res[i]);}puts("");
}void dfs(int num)
{if (res.size() == m){Print();return;}for (int i = num; i <= n; i++){if (!st[i]){st[i] = true;res.push_back(i);if (res.size() == 1 && res[0] > (n-m+1)){res.pop_back();st[i] = false;continue;}dfs(i + 1);st[i] = false;res.pop_back();}}
}int main(void)
{scanf("%d %d", &n, &m);dfs(1);return 0;
}
解法二
#include<iostream>
#include<vector>int n, m;
std::vector<int>res;
bool st[30];void dfs(int start)
{if(res.size()==m){for(int i=0;i<res.size();i++){printf("%d ",res[i]);}puts("");return;}for(int i=start;i<=n;i++){res.push_back(i);dfs(i+1);res.pop_back();}
}int main(void)
{scanf("%d %d", &n, &m);dfs(1);return 0;
}
相关文章:

递归实现组合型枚举
递归实现组合型枚举 #include<iostream> #include<vector>int n, m; std::vector<int>res; bool st[30];void Print() {for(int i0;i<res.size();i){printf("%d ",res[i]);}puts(""); }void dfs(int num) {if (res.size() m){Print(…...

SCAU:1065 数组中的指针
1065 数组中的指针 时间限制:1000MS 代码长度限制:10KB 提交次数:3436 通过次数:1692 题型: 编程题 语言: G;GCC Description 设有如下数组定义: int a[3][4]{{1,3,5,7},{9,11,13,15},{17,19,21,23}}; 计算下面各项的值(设数组a的首地址为2000&…...

找不到msvcp110.dll如何修复?分享5个亲测有效的修复方法
在计算机使用过程中,我们经常会遇到一些错误提示,其中之一就是“msvcp110.dll丢失”。这个错误通常发生在运行某些程序时,系统无法找到所需的动态链接库文件。那么,msvcp110.dll到底是什么呢?它又有什么作用࿱…...

LeetCode刷题笔记第80题:删除有序数组中的重复项 II
LeetCode刷题笔记第80题:删除有序数组中的重复项 II 题目: 删除升序数组中超过两次的元素后的数组长度 想法: 使用快慢指针的方法完成,使用快指针遍历整个数组,使用慢指针完成相同元素最多保留两个。在快指针遍历到…...

【开源存储】minio对象存储部署实践
文章目录 一、前言1、介绍说明2、部署方式3、冗余模式4、约束限制4.1、规格参数4.2、API支持a、minio不支持的Amazon S3 Bucket APIb、minio不支持的Amazon S3 Object API 二、部署说明1、软件安装2、minio单机部署3、minio分布式部署3.1、前置条件3.2、开始运行3.3、操作说明 …...
)
Java编程强化练习(二)
表达式计算(支持空格,连乘,连除)(选做题,不计分) 【问题描述】 从标准输入中读入一个整数算术运算表达式,如5 - 1 * 2 * 3 12 / 2 / 2 。计算表达式结果,并输出。 …...

Redis的高可用模式
1. 什么是高可用? 高可用(High Availability, HA)是指在信息技术中确保系统、服务或应用程序在绝大多数时间内都是可操作和可访问的能力。这通常涉及以下几个关键方面: 最小化停机时间: 高可用系统的目标是减少因硬件故障、系统升…...
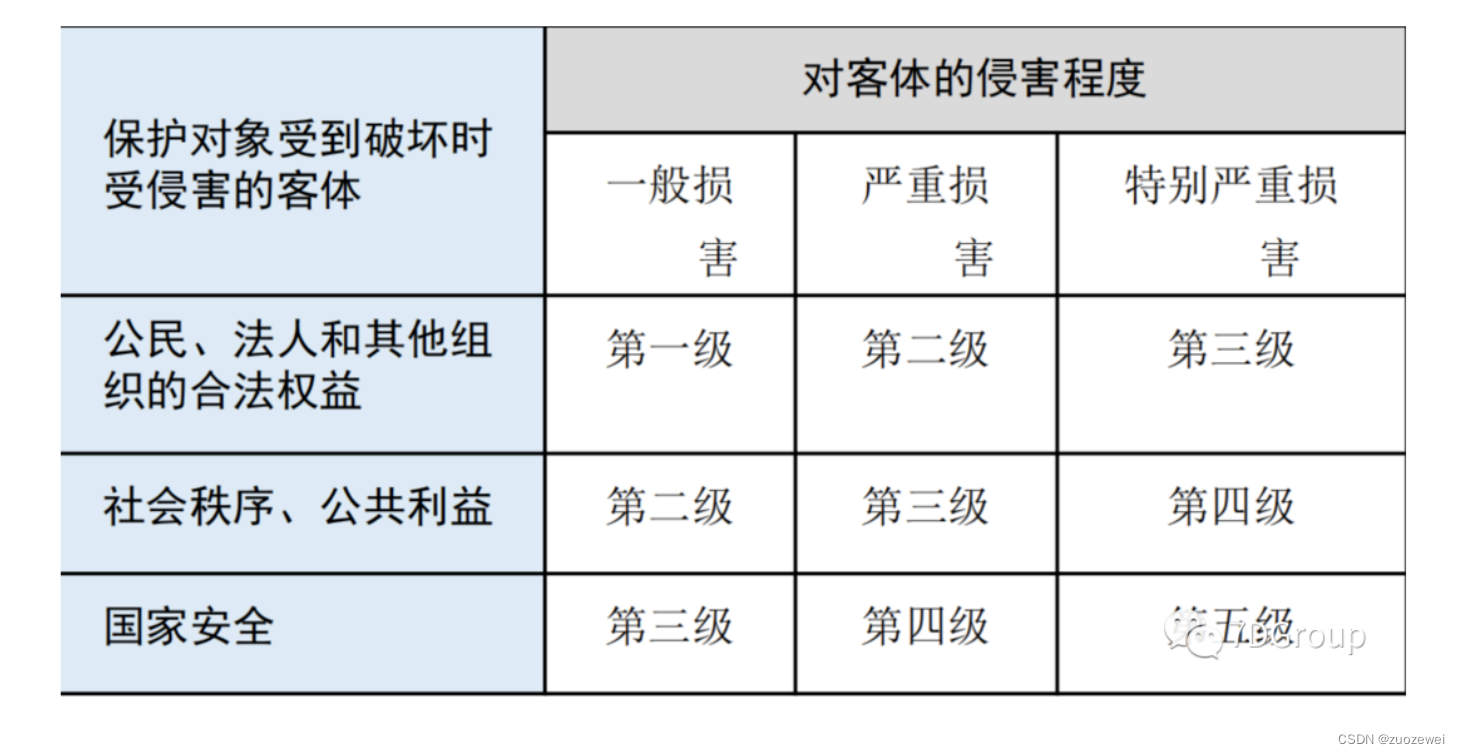
非功能关键知识总结(一)
文章目录 一、稳定性(一)、服务级别协议1、SLA2、OLA3、UC (二)、可用性指标(三)、突发事件等级 三、质量(一)、千行代码缺陷数量(二)、软件质量模型的发展(三)、产品质量模型 四、安全(一)、网络安全 五、灾备(一)、灾备指标(二)、灾难恢复等级(三)、容灾技术分类 一、稳定性 …...

时间序列趋势检验相关检验方法:斜率法、Cox-Stuart检验、Mann-Kendall检验
文章目录 1.斜率法1.1.原理1.2.优缺点1.3.Python代码2.Cox-Stuart检验2.1.原理2.2.优缺点2.3.Python代码3.Mann-Kendall 检验3.1.原理3.1.1.假设前提3.1.2.趋势检验3.1.3.S到Z的变换原理3.1.4.Var(s)是如何得到的3.1.5.衡量趋势的指标:倾斜度...
Redis相关知识
yum安装redis 使用以下命令:直接将redis安装到Linux服务器(Xshell)中 yum -y install redis 启动redis 使用以下命令,以后台运行方式启动redis redis-server /etc/redis.conf & 操作redis 使用以下命令启动redis客户端 redis-…...

数据管理系统-week10-自由访问控制
文章目录 前言一、用户管理用户管理语句介绍二、数据库管理三、特权(重点考点)Administrative (global) privileges数据库特权表权限列权限四、角色参考文献前言 这节课主要讲了用户管理数据库的具体语句,数据库特权当中的全局特权,数据库特权,表特权与列特权的使用与注意…...
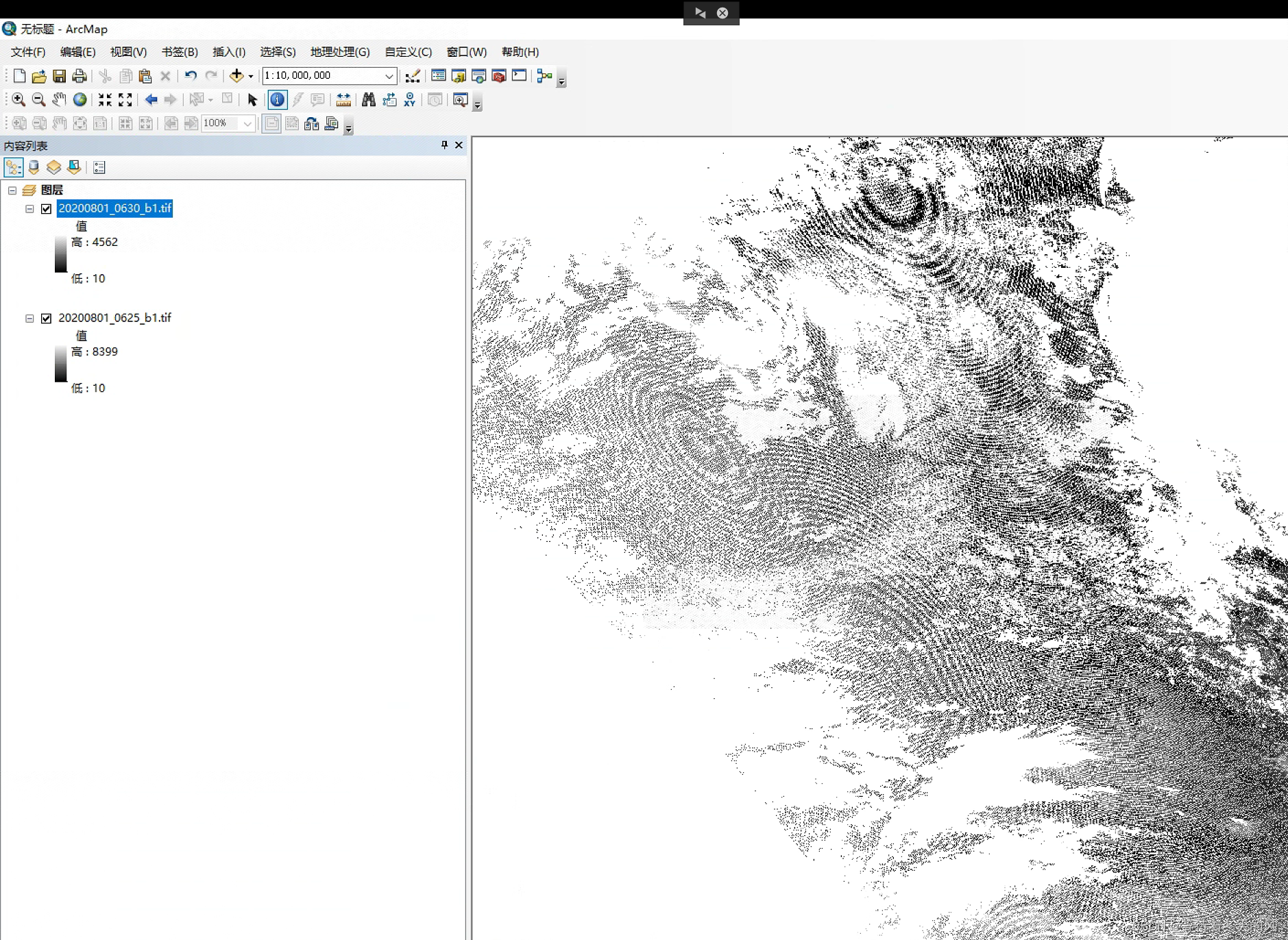
Python遥感开发之批量拼接
Python遥感开发之批量拼接 1 遥感图像无交错的批量拼接2 遥感图像有交错的批量拼接 前言:主要借助python实现遥感影像的批量拼接,遥感影像的批量拼接主要分为两种情况,一种是遥感图像无交错,另一种情况是遥感图像相互有交错。具体…...

【bat】批处理脚本大全
目录 1.概述 2.变量 3.运算符 3.2.重定向运算符 3.3.多命名运算符 3.4.管道运算符 4.命令 4.1.基本命令 4.2.参数传递 4.3.查看脚本内容 4.4.注释 4.5.日期和时间 4.6.启动脚本 4.7.调用其他bat 4.8.任务管理 4.8.1.任务列表查看 4.8.2.任务终止 4.9.文件夹 …...
java设计模式学习之【单例模式】
文章目录 引言单例模式简介定义与用途实现方式:饿汉式懒汉式 UML 使用场景优势与劣势单例模式在spring中的应用饿汉式实现懒汉式实现数据库连接示例代码地址 引言 单例模式是一种常用的设计模式,用于确保在一个程序中一个类只有一个实例,并且…...
UWB高精度定位系统项目源码
在现代社会中,精准定位技术对于各行各业都至关重要。为了满足对高精度定位的需求,超宽带(Ultra-Wideband, UWB)技术应运而生。UWB高精度定位系统以其出色的定位精度和多样化的应用领域而备受关注。本文将深入探讨UWB高精度定位系统…...
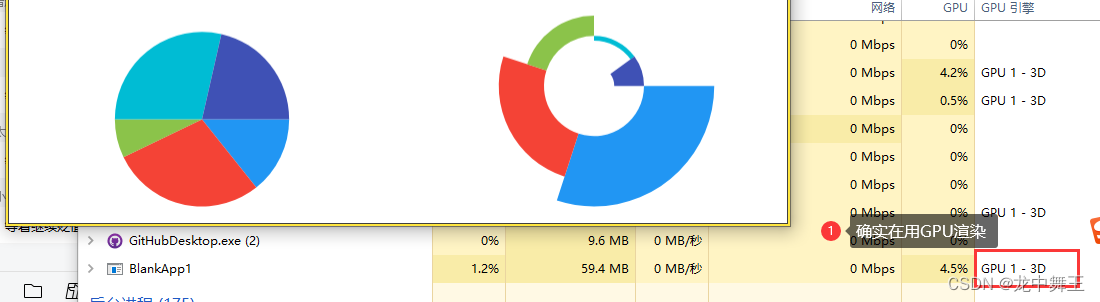
WPF Live Charts2 自学笔记
文章目录 前言实现效果微软平台的历史问题 WPF 项目搭建Nuget添加额外框架添加项目初始化livecharts配置其它LiveCharts2 案例简单案例Demo示例ViewViewModel GPU渲染 Github地址仓库 前言 LiveChart 是C# 上面很受欢迎的统计图 UI控件。最近在学WPFhalcon开发,想想…...
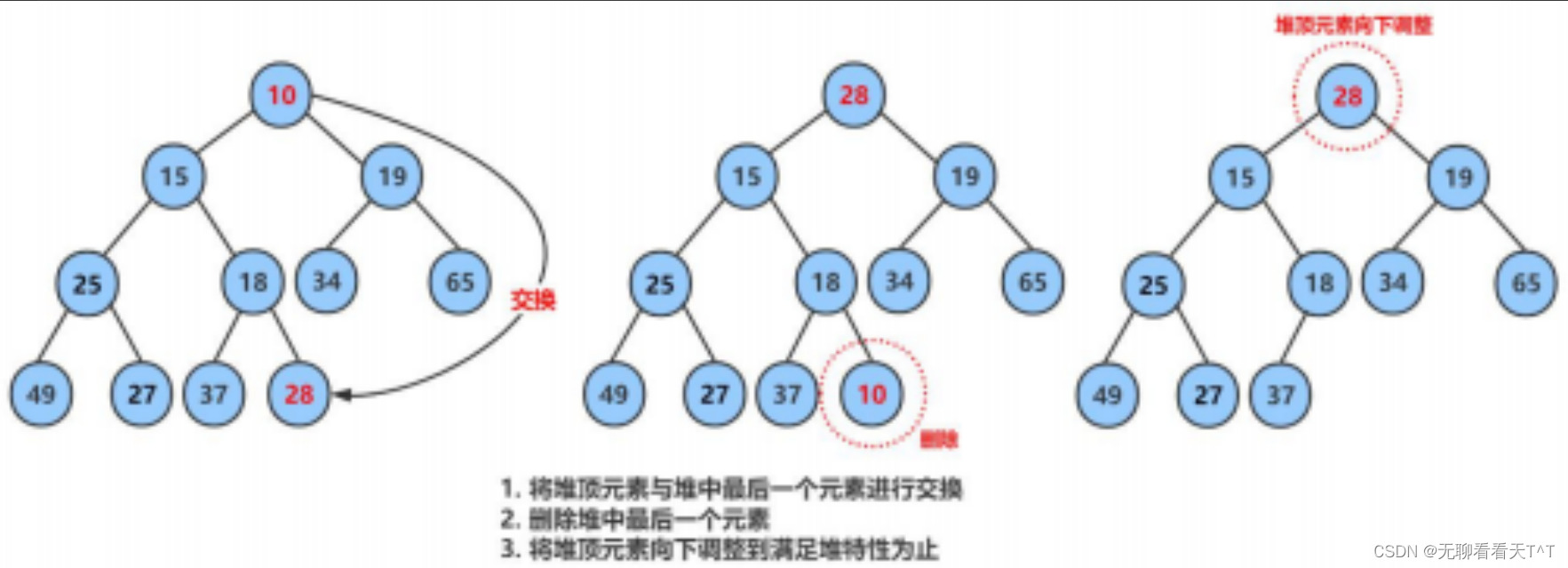
大小堆的实现(C语言)
目录 前言 一种完全二叉树:堆 堆的概念 堆的性质 建堆的时间复杂度 建堆的空间复杂度: 小堆的实现 必要补充 堆的初始化 堆的销毁 向上调整算法 堆的插入 向下调整算法 堆的删除 获取堆顶元素 获取堆中元素个数 堆的判空 最终代码 He…...
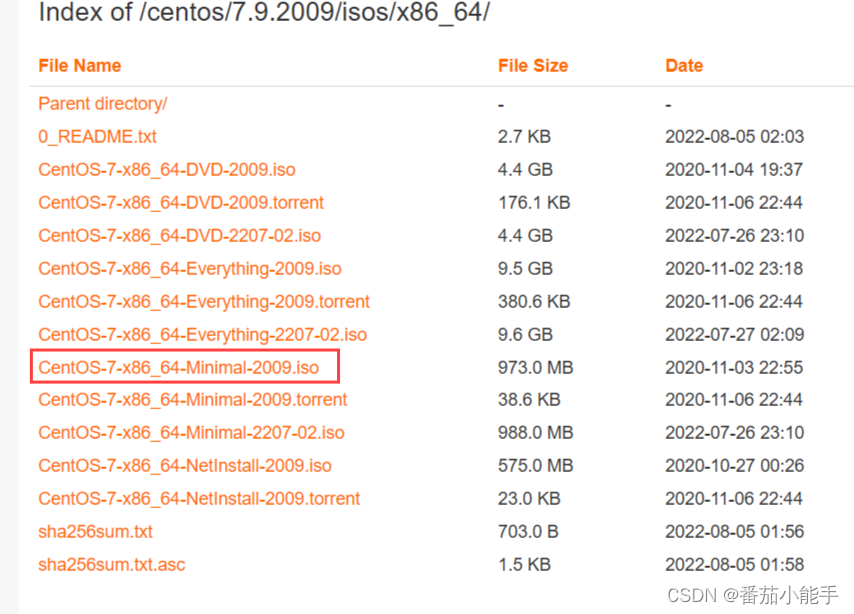
Linux系统之centos7编译安装Python 3.8
前言 CentOS (Community Enterprise Operating System) 是一种基于 Red Hat Enterprise Linux (RHEL) 进行源代码再编译并免费提供给用户的 Linux 操作系统。 CentOS 7 采用了最新的技术和软件包,并提供了强大的功能和稳定性。它适用于各种服务器和工作站应用场景&a…...

Lambda表达式与方法引用
作者简介:大家好,我是smart哥,前中兴通讯、美团架构师,现某互联网公司CTO 联系qq:184480602,加我进群,大家一起学习,一起进步,一起对抗互联网寒冬 引子 先来看一个案例 …...
)
二维数组处理(一)
输入整型二维数组a(5行5列),完成如下要求: 输出二维数组a。 将a的第2行和第4行元素对调后,形成新的二维数组a并按行输出,每个元素之间隔一个空格。(行号从0开始计算)。 用对角线(指二维数组左…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
