树与二叉树堆:经典OJ题集(2)
目录
二叉树的性质及其问题:
二叉树的性质
问题:
一、对称的二叉树:
题目:
解题思路:
二、另一棵树:
题目:
解题思路:
三、翻转二叉树:
题目:
解题思路:
四、层序遍历:
概念:
核心代码:
衍生问题:
1、一层一层的打印结点元素
思路分析:
代码分析:
代码演示:
2、判断是否是完全二叉树
思路分析:
代码演示:
队列代码:
头文件:
源文件:

二叉树的性质及其问题:
二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是 .
3. 对任何一棵二叉树, 度为0的结点 始终 比 度为 2 的结点个数多1 ,当结点个数是奇数时度为1的结点个数是1
4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= log 2 (n+1). (ps: 是 log以2 为底,n+1为对数),又可以将高度 h 和 结点个数 换算为公式 [2^(h-1),2^h -1 ] 结点个数就在这个区间至内。
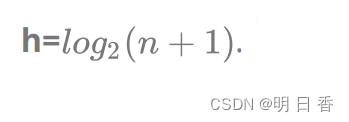
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对 于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1>=n 否则无左孩子
- 若2i+2>=n 否则无右孩子
问题:
1、在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
解答:
2、一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
解答:使用[2^(h-1),2^h -1 ] 进行带入判断
3、一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
解答:
一、对称的二叉树:
题目:
给你一个二叉树的根节点
root, 检查它是否轴对称。
题源:101. 对称二叉树 - 力扣(LeetCode)
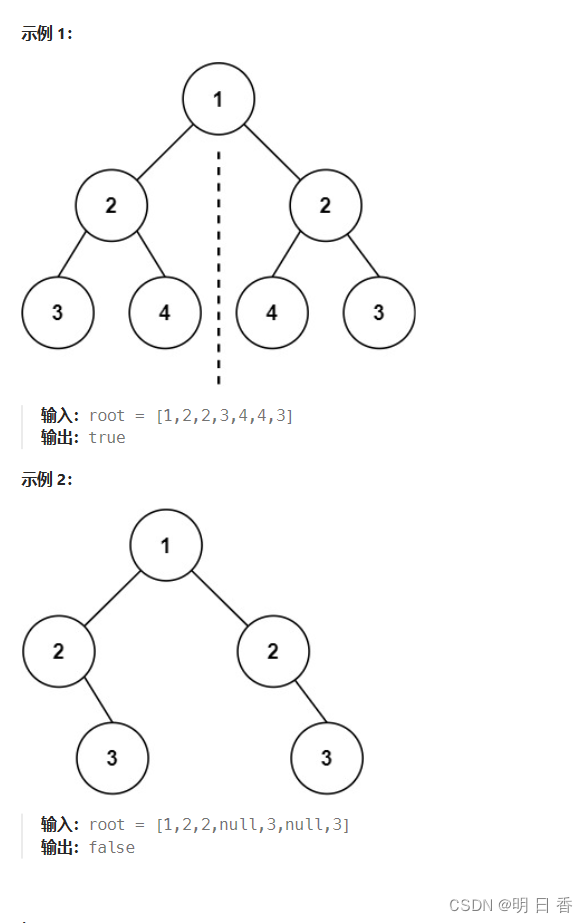
解题思路:
按照图例来看,若想判断一个二叉树是否是图中的样子,那么需要将将二叉树分为两个部分,也就说将一棵二叉树当成两个部分,除去根结点,对左右子树部分进行相对应的比较。
也就说将左子树部分的左孩子和右子树部分的右孩子进行比较和左子树的右孩子和右子树的左孩子进行比较,将比较分为两个部分进行。
- 所以本题是将二叉树分为两个子树,而又将两颗子树的左右孩子进行分开配对比较。


二、另一棵树:
题目:
- 给你两棵二叉树
root和subRoot。检验root中是否包含和subRoot具有相同结构和节点值的子树。如果存在,返回true;否则,返回false。- 二叉树
tree的一棵子树包括tree的某个节点和这个节点的所有后代节点。tree也可以看做它自身的一棵子树。
题源:572. 另一棵树的子树 - 力扣(LeetCode)

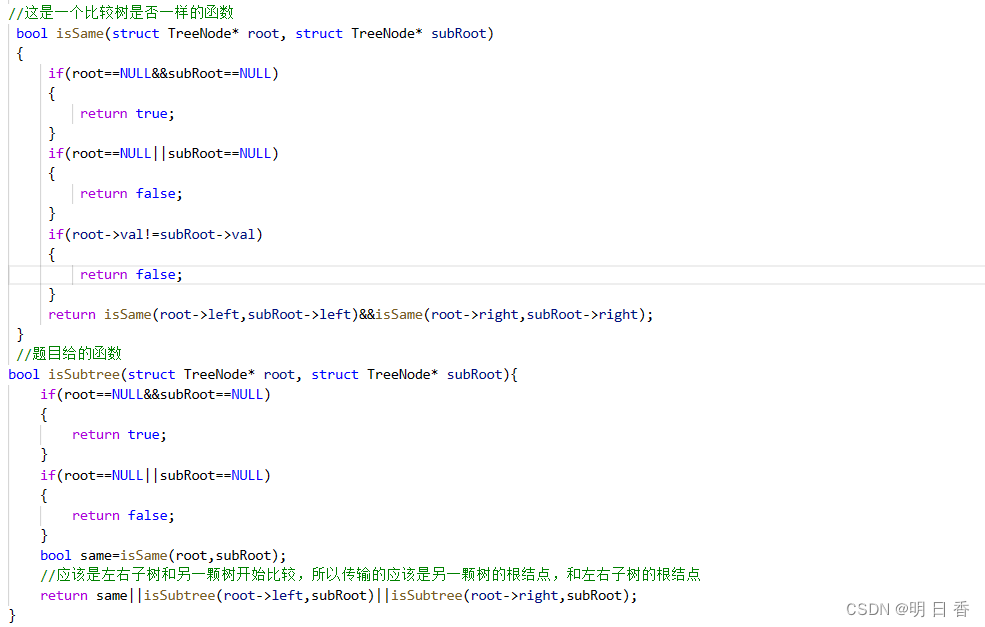
解题思路:
如图所示,我们需要检查一颗大树内部是否有着小树的存在,即大树的内部是否包含了小数,与之前的<查找两棵树是否相同:100. 相同的树 - 力扣(LeetCode)>类似。
也需要用到这一题的代码进行查询,而在查询之前,我们首先将本题的查找分为三个部分,第一,从根结点开始找,第二从左子树开始找,第三从右子树开始找。
从三个方面开始寻找,寻找的过程中可以很显然意见的发现,问题被化解为了以查询是否和小树同时存在该结点,如果同时存在结点的数值是否和小树的一样。
- 如果都一样,那么再度开始进行调用遍历,查询下一个结点是否一致。

三、翻转二叉树:
题目:
给你一棵二叉树的根节点
root,翻转这棵二叉树,并返回其根节点。
题源:226. 翻转二叉树 - 力扣(LeetCode)

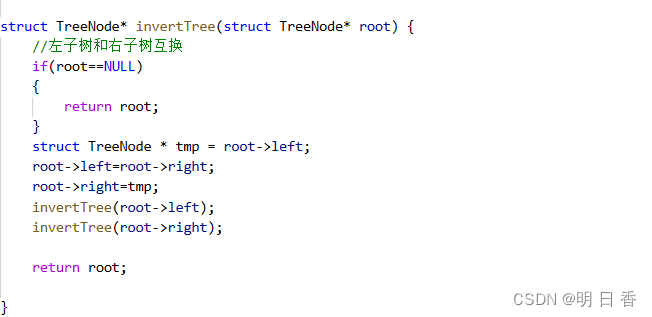
解题思路:
- 如图例所示,翻转二叉树是将左右子树进行交换,且并不是单纯的一次交换,而是以每个结点为根结点,其下的左右孩子结点进行了交换。
所以,面对这种问题可以采取一个非常简单的思路,交换地址,因为我们当前的二叉树结构是链式二叉树,所以在链式二叉树中的左右孩子结点的指针是地址,所以只要把左右孩子结点的指针内部的地址进行交换即可。
四、层序遍历:
概念:
层序遍历是二叉树遍历的一种,且是在二叉树的四种遍历中较为复杂的一种,因为层序遍历需要使用到队列。
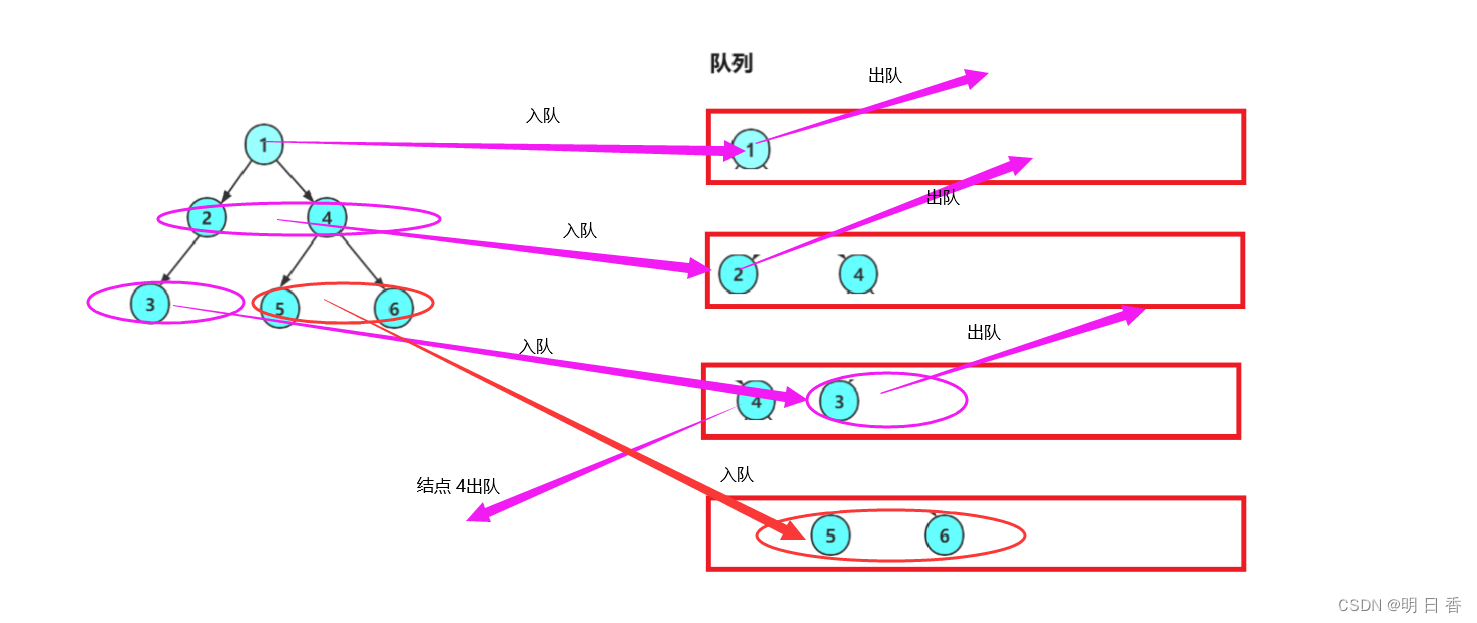
如图所示,层序遍历便是将二叉树中的每一层的结点放入队列中,以入队的形式存放到队列中,而当每一个结点进入后,又会马上的出队,且出 队后会将该结点的左右孩子结点送入队列中,等到队列完全为空时,层序遍历才遍历完成。
而在层序遍历中,我们需要用到的队列函数有:入队、出队、判断队列是否为空、获取队头元素,其中,判断队列是否为空是判断层序遍历是否结束的语句,获取队头元素是为了方便出队,入队则是要结点的左右孩子结点进入队内。
核心代码:

代码分析

衍生问题:
1、一层一层的打印结点元素


思路分析:
如上图所示,要求我们将结点的元素如图所示进行打印,而这种打印也就是将每一层都使用 \n 进行隔离,而需要使用 \n 进行隔离,可以转化为,如何将每一层完美的分离。
- 这里就需要用到队列的一个特点,先进先出,因为每一次出去的结点都会将它的左右孩子结点带入队列中,所以可以计算孩子结点的个数作为循环判断。

代码分析:
假设当前这一层的结点个数是N,那么在出队的同时会带入孩子结点,当这一层的结点全部出队,而在对内,当前这一层的结点个数是0,而孩子结点则是2N(假设每一个结点都有左右孩子结点),然后以结点个数是否是0为判断,跳出了循环,随后打印回车,随后又因为队列不为空而进入层序遍历,同时再次之前进行孩子结点的个数统计,准备进行下一层的循环。
代码演示:

2、判断是否是完全二叉树
完全二叉树概念:树与二叉树堆:二叉树-CSDN博客
思路分析:
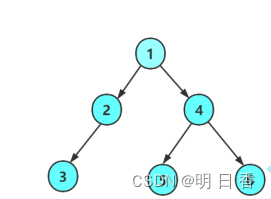
如图所示,如果不是完全二叉树,那么按照层序遍历的思想,那么在层序遍历时必然会有一个结点没有带入它的左右孩子结点,因为它的左右孩子结点不存在或者说是NULL。
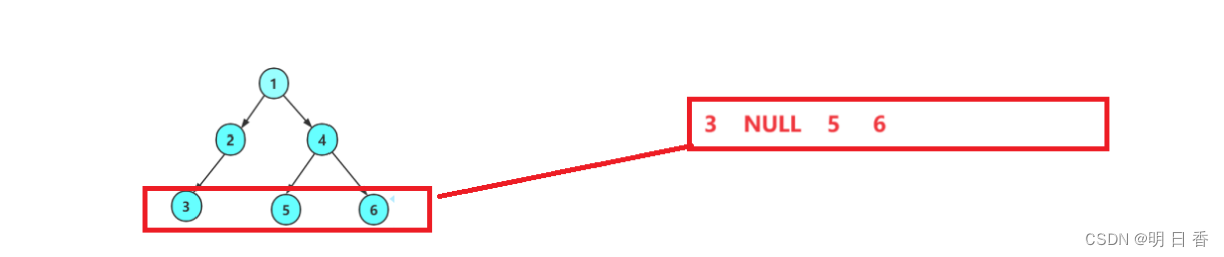
而本题中,我们可以取消对左右孩子结点是否存在的判断,从而当最后出队时,必然会出现值为NULL的结点出队,所以以此来进行判断。
当出现NULL之后,队列内还有元素(结点)存在,那么这颗树便不是完全二叉树。
代码演示:

队列代码:
头文件:

源文件:


相关文章:

树与二叉树堆:经典OJ题集(2)
目录 二叉树的性质及其问题: 二叉树的性质 问题: 一、对称的二叉树: 题目: 解题思路: 二、另一棵树: 题目: 解题思路: 三、翻转二叉树: 题目:…...
-------连载(40))
Java面试题(每天10题)-------连载(40)
目录 Mysql篇 1、表中有大字段X(例如:text类型),且字段X不会经常更新,将该字段拆成子表好处是什么? 2、Mysql中InnoDB引擎的行锁是通过加载什么上完成的? 3、Mysql中控制内存分配的全局参数…...

2023年【起重机司机(限桥式起重机)】报名考试及起重机司机(限桥式起重机)考试资料
题库来源:安全生产模拟考试一点通公众号小程序 2023年【起重机司机(限桥式起重机)】报名考试及起重机司机(限桥式起重机)考试资料,包含起重机司机(限桥式起重机)报名考试答案和解析及起重机司机(限桥式起重机)考试资料练习。安全生产模拟考试一点通结合…...
Linux的基本指令(3)
目录 制作小文件&查看 nano指令 cat指令 tac指令 制作大文件&查看 一切皆文件 echo指令 > 输出重定向 以写"w"的形式打开文件 以追加"a"的形式打开文件 cat指令 < 输入重定向 创建big.txt more指令 less指令(推…...

C语言memcpy,memmove的介绍及模拟实现
文章目录 每日一言memcpy介绍模拟实现 memmove介绍模拟实现思路代码 结语 每日一言 If you want to lift yourself up, lift up someone else. 如果你想振奋自己, 先振奋周遭的人。 memcpy 介绍 函数原型: void *memcpy(void *dest, const void *sr…...
克服.360勒索病毒:.360勒索病毒的解密和预防
导言: 在数字化的今天,数据安全问题变得愈发棘手。.360勒索病毒是当前网络空间的一场潜在灾难,对于这个威胁,了解应对之道和采取切实的预防措施至关重要。如果您正在经历勒索病毒的困境,欢迎联系我们的vx技术服务号(s…...

21、Resnet50 中包含哪些算法?
(本文已加入“计算机视觉入门与调优”专栏,点击专栏查看更多文章信息) 这一节汇总一下resnet50 中包含的算法,并且简单介绍。 总共卷积算法、激活算法(relu)、最大池化算法、加法(主要是为了实现残差结构)、全局平均池化、全连接和 softmax 算法这几种算法。 卷积 卷…...
pybind11教程
pybind11教程 文章目录 pybind11教程1. pybind11简介2. cmake使用pybind11教程3. pybind11的历史 1. pybind11简介 项目的GitHub地址为: pybind11 pybind11 是一个轻量级的头文件库,用于在 Python 和 C 之间进行互操作。它允许 C 代码被 Python 调用&am…...

Java基础- 自定义类加载器
自定义类加载器 在 Java 中实现自定义类加载器通常涉及继承 ClassLoader 类并重写其 findClass 方法。自定义类加载器允许我们从非标准来源(如网络、加密文件或其他媒体)加载类。下面是实现自定义类加载器的基本步骤: 1. 继承 ClassLoader …...

2022年高校大数据挑战赛A题工业机械设备故障预测求解全过程论文及程序
2022年高校大数据挑战赛 A题 工业机械设备故障预测 原题再现: 制造业是国民经济的主体,近十年来,嫦娥探月、祝融探火、北斗组网,一大批重大标志性创新成果引领中国制造业不断攀上新高度。作为制造业的核心,机械设备在…...
洛谷 P1998 阶乘之和 C++代码
前言 今天我们来做洛谷上的一道题目。 网址:[NOIP1998 普及组] 阶乘之和 - 洛谷 西江月夜行黄沙道中 【宋】 辛弃疾 明月别枝惊鹊,清风半夜鸣蝉。稻花香里说丰年,听取WA声一片。 七八个星天外,两三点雨山前。旧时茅店社林边&…...
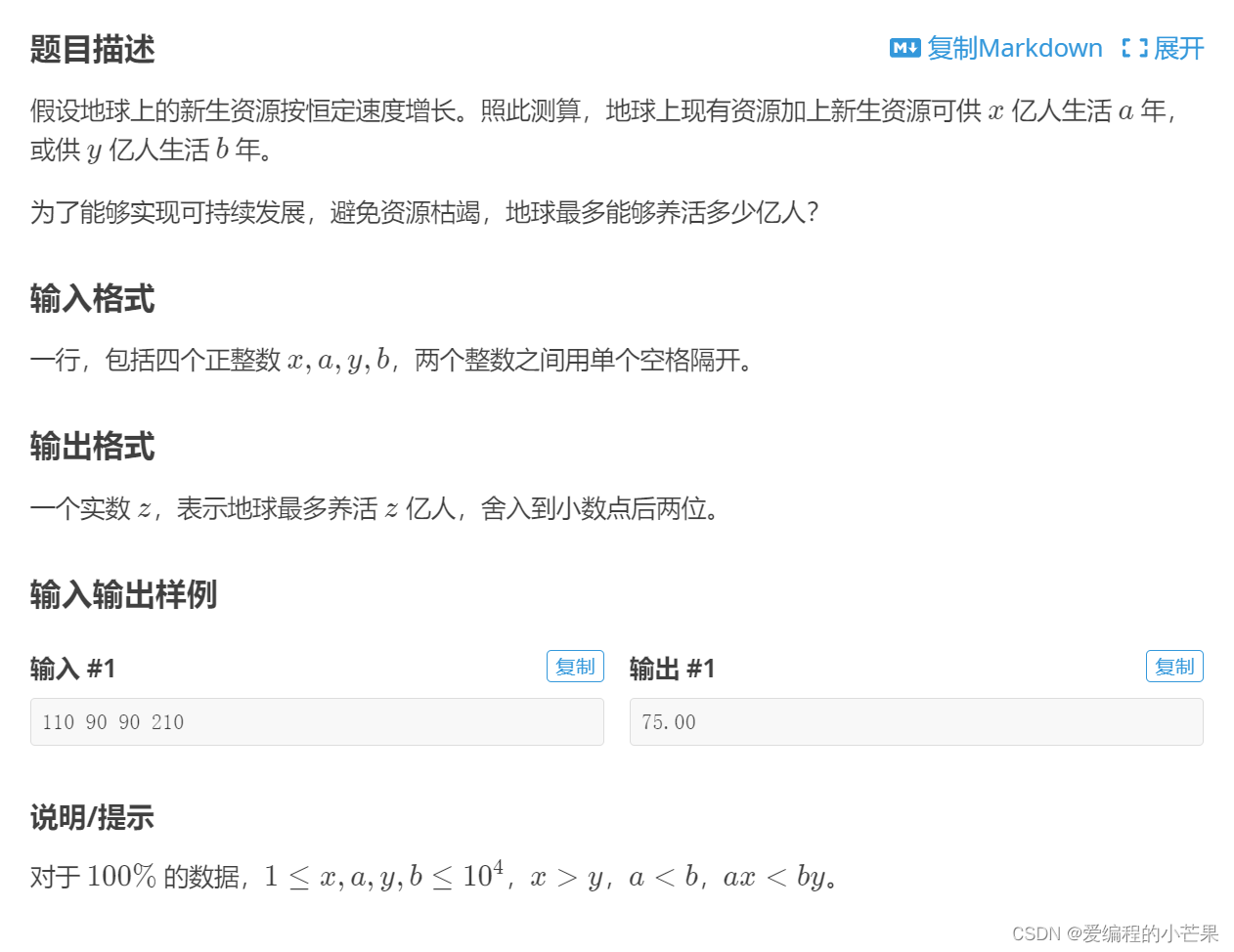
洛谷 B2006 地球人口承载力估计 C++代码
目录 前言 思路点拨 AC代码 结尾 前言 今天我们来做洛谷上的一道题目。 网址:地球人口承载力估计 - 洛谷 题目: 思路点拨 经典牛吃草问题。 解设一个人一年吃一份草。 则x*a-y*b为会多出的草,为什么会多呢?是因为每年都有…...

少走弯路:OpenCV、insightface 等多方案人脸推理和识别
脑壳有包又花时间折腾了一下,其实之前也折腾过,主要是新看了一个方法 在下图中查找脸部 第一种方案: 使用了opencv 的cv2.FaceDetectorYN. ,完整代码如下: import numpy as np import cv2imgcv2.imread("00000…...

github代码连接vercel 建立一个公用网站
Deploying to the Cloud using Vercel 前置任务 建立一个基于flask的web app代码库并上传至github repo Vercel用途 vercel有点像一个免费的cloud server,帮助你将flask框架下的程序运行在云端。可以public访问。 deploy流程 在主文件夹中建立requirements.tx…...

使用pandas将字符串格式数据转换为单独的行
有时在处理数据时,可能会遇到这样的情况,即数据框中的整个字符串条目需要拆分到不同的行中。这可能是一项具有挑战性的任务,特别是当数据庞大而复杂时。尽管如此,一个名为pandas的Python库提供了各种函数,使用这些函数…...
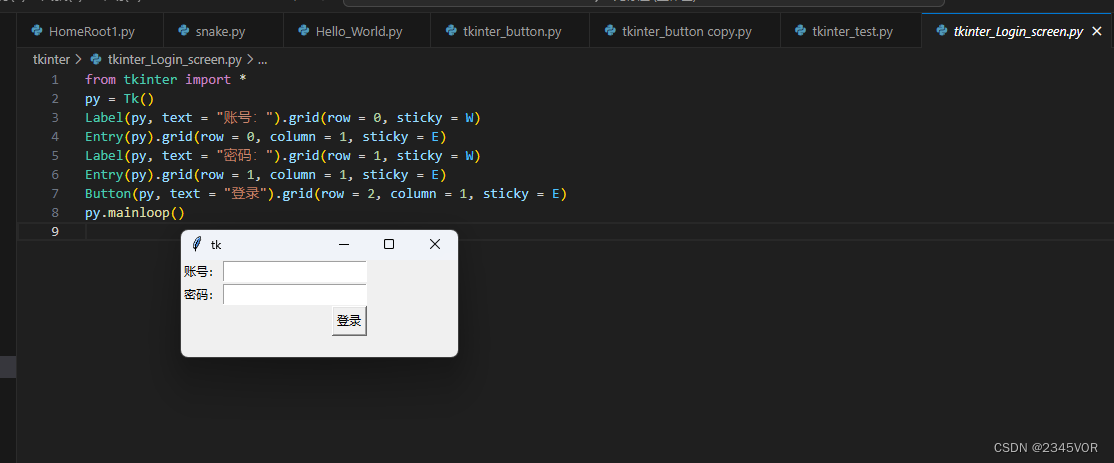
【Tkinter 入门教程】
【Tkinter 入门教程】 1. Tkinter库的简介:1.1 GUI编程1.2 Tkinter的定位 2. Hello word! 程序起飞2.1 第⼀个程序2.2 字体颜色主题 3. 组件讲解3.1 tkinter 的核⼼组件3.2 组件的使⽤3.3 标签Label3.3.1 标签显示内容3.3.2 多标签的应⽤程序3.3.3 总结 3.4 按钮but…...

深入理解Java中继承的高级使用方案
摘要: 继承是Java中的一项强大的特性,它允许子类从父类中继承属性和方法。然而,继承的高级使用方案涉及更复杂的概念和技术,可以帮助开发人员构建更加灵活、可维护和可扩展的代码。本文将深入探讨Java中继承的高级用法,…...
nexus私服开启HTTPS
maven3.8.1以上不允许使用HTTP服务的仓库地址,如果自己搭建的私服需要升级为HTTPS或做一些设置,如果要升级HTTPS服务有两种方式:1、使用Nginx开启HTTPS并反向代理nexus;2、直接在nexus开启HTTPS。这里介绍第二种方式 1、在ssl目录…...

融合CFPNet的EVC-Block改进YOLO的太阳能电池板缺陷检测系统
1.研究背景与意义 项目参考AAAI Association for the Advancement of Artificial Intelligence 研究背景与意义 随着太阳能电池板的广泛应用,对其质量和性能的要求也越来越高。然而,由于生产过程中的各种因素,太阳能电池板上可能存在各种缺…...

传媒行业CRM:打造高效客户管理,提升品牌影响力
传媒行业充满竞争和变化,传媒企业面临着客户管理不透明、业务流程混乱、销售数据分析不足,无法优化营销策略和运营管理等问题。CRM系统是企业实现数智化管理的神器,可以有效解决这些问题。下面说说,传媒行业CRM系统推荐。 1、建立…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...


