正是阶段高等数学复习--函数极限的计算
之前在预备阶段中函数极限的解决方式分三步,第一步观察形式并确定用什么方式来解决,第二步化简,化简方式一共有7种,分别是最重要的三种(等价替换、拆分极限存在的项、计算非零因子)以及次重要的4种(根式有理化、提公因子、倒代换、幂指函数指数化),第三步是计算(泰勒公式和洛必达法则),每做完一步就要先观察,化简式子。
在基础阶段中更加简洁了一下,函数极限的计算一共有五个方法:利用基本极限求极限、利用等价无穷小求极限、利用有理运算法则求极限、利用洛必达法则求极限、利用泰勒公式求极限,这样更加简洁了,比如我们观察形式的时候发现是0/0型,那我们就考虑用等价替换或者是洛必达或泰勒公式来解决,若是1^无穷型,则利用基本极限中x->0,(1+x)^1/x=e的扩展的三部曲来解决等等。
首先第一个方法:利用基本极限求极限(9个),分别是x->0,sinx/x;x->0,(1+x)^1/x=e;x->无穷,(1+1/x)^x=e(这里注意,x->无穷,(1+x)^1/x = ?或者x->0,(1+1/x)^x = ?,首先幂指函数的底数一定>0所以上述两个极限都不存在,因为左右极限有一边是不存在的,其次若只求存在的那一边,结果等于什么,我们可以用幂指函数指数化然后结合方法来求,最后结果为1);x->0,a^x-1/xlna=1;x->无穷,n^1/n=1(这个可以用幂指函数指数化来求得);x->无穷,a^1/n=1,多项式求极限(抓大头,当x->无穷时,取指数高的,当x->0时,取指数低的);n->无穷,x^n=(|x|>1,=无穷,|x|<1,=0,x=1,=1,x=-1,不存在);n->无穷,e^nx也是分情况讨论(x>0,x<0以及x=0)。我们将1^无穷型展开来说它的三步走:化为(1+f(x))^g(x)的形式;写成e^f(x)*g(x)的形式,最后得答案,推理过程不多说了。
第二个方法:利用等价无穷小求极限,乘除法中能用,加减法中也能用(a---a1,b---b1,a-b---a1-b1,前提是a/b!=1;;a---a1,b---b1,a+b---a1+b1,前提是a/b!=-1),这个规则一定要搞清,下面就是一阶二阶三阶无穷小,一阶(sinx---x;tanx---x;arcsinx---x;arctanx---x;a^x-1---xlna;e^x-1---x;ln(1+x)---x;(1+f(x))^g(x)-1---f(x)*g(x))二阶(1-cosx---1/2*x^2;ln(1+x)-1----1/2*x^2;e^x-1-x---1/2*x^2)三阶(sinx-x----1/6*x^3;arcsinx-1---1/6*x^3;tanx-x---1/3*x^3;arctanx-x----1/3*x^3)
第三个方法:利用有理运算法则求极限(其实是包含了拆分极限存在的项和计算非零因子),最初我们认为当x->x0时,f(x)+/-*g(x)只有当两个极限都存在的时候才能拆开,但是加减的时候有一个存在就可以拆开,因为另外一个如果是存在的则整体也是存在的,若另一个不存在则整体也是不存在的;在乘除法中若有一个是存在且不为0的就可以计算出来,一定是不为0,而且这个因子一定是相对整个函数是因子才能计算。当x->x0时,若f(x)/g(x)存在,且x->x0,g(x)=0,则x->x0,f(x)=0,即分母趋向于0,分子也趋向于0(f(x)=f(x)/g(x)*g(x),0*有界一定=0);当x->x0时,若f(x)/g(x)存在但不等于0,且x->x0,f(x)=0,则x->x0,g(x)=0,即分子趋向于0,分母也趋向于0(例如当x->0时,sinx/1+x^2=0,sinx->0,但1+x^2=0->2)
第四个方法:利用洛必达法则求极限(0/0或无穷/无穷都可以用,但是使用前有前提,就是使用完后极限还是存在的,一般做题的时候使用都存在)
第五个方法:利用泰勒公式(带皮埃诺余项的泰勒公式)求极限
前提是x=x0时n阶可导,特别是x=0时n阶可导我们使用麦克劳林公式
sinx、arcsinx、tanx、arctanx、cosx、e^x-1、ln(x+1)、(1+x)^a这八个比较重要

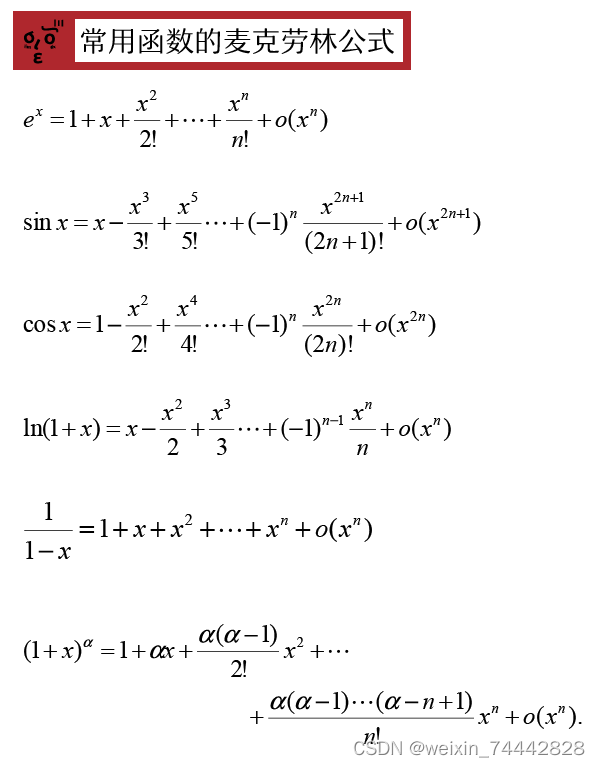
相关文章:
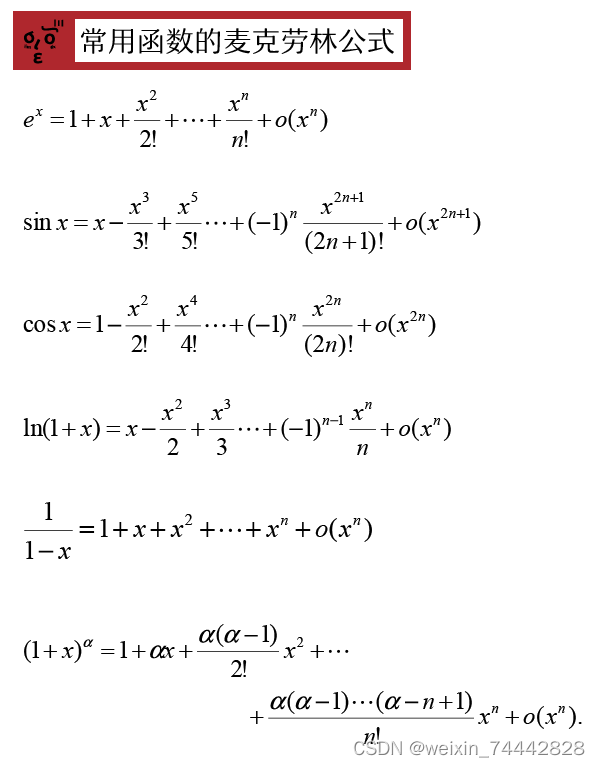
正是阶段高等数学复习--函数极限的计算
之前在预备阶段中函数极限的解决方式分三步,第一步观察形式并确定用什么方式来解决,第二步化简,化简方式一共有7种,分别是最重要的三种(等价替换、拆分极限存在的项、计算非零因子)以及次重要的4种…...

Linux-usb触摸板去除鼠标箭头
usb触摸板会同时加载hid-generic.c和hid-multitouch.c驱动 [ 213.602561] usb 4-1: new full-speed USB device number 2 using ohci-platform [ 213.834953] usb 4-1: New USB device found, idVendor6615, idProduct108c, bcdDevice 1.30 [ 213.835048] usb 4-1: New USB…...

【微信小程序】英文字母不换行问题 flex布局字符超出宽度折行问题:设置了word-break: break-all;和flex: 1;冲突flex不生效问题
flex布局中英文字符超出宽度不会自动折行的问题,但是设置了word-break: break-all;前面设置的flex: 1;就不生效了 1.英文字母不换行问题 .view_text {word-break: break-all; }如果使用flex仅仅设置word-break: break-all;是会影…...

python--自动化办公(Word)
python自动化办公之—Word python-docx库 1、安装python-docx库 pip install python-docx2、基本语法 1、打开文档 document Document() 2、加入标题 document.add_heading(总标题,0) document.add_heading(⼀级标题,1) document.add_heading(⼆级标题,2) 3、添加文本 para…...
sourceTree的下载和安装
sourceTree的下载和安装 一、概述 SourceTree 是一款免费的 Git 和 Hg 客户端管理工具,支持 Git 项目的创建、克隆、提交、push、pull 和合并等操作。它拥有一个精美简洁的界面,大大简化了开发者与代码库之间的 Git 操作方式,这对于不熟悉 …...

解决:ModuleNotFoundError: No module named ‘PyQt5‘
解决:ModuleNotFoundError: No module named ‘PyQt5’ 文章目录 解决:ModuleNotFoundError: No module named PyQt5背景报错问题报错翻译报错位置代码报错原因解决方法安装PyQt5在PyCharm中配置PyQt5对于新项目对于已有项目 今天的分享就到此结束了 背景…...

极客时间 - 如何成为学习高手【文章笔记 + 思考总结】
如何成为学习高手【文章笔记 思考总结】 高度自律 高度自律 5分钟起步法。 稍微走在计划前面。 替代拖延法。 自律:从不自律的念头中,约束自己。有变弱倾向时进行对抗。 在一种痛苦和另一种痛苦之间做选择,选择那个有意义的痛苦。 在某些固…...

前端笔记(二):CSS 选择器与特性
CSS(层叠样式表)是一种样式表语言,用于描述HTML或XML文档的呈现方式。它定义了如何在屏幕、纸张或其他媒体上显示文档的样式、布局和外观。 里面的代码由 选择器 { } 组成 体验 CSS CSS 可以让我们界面变得更加美观,这是 CSS 的…...
【每日一题】1423. 可获得的最大点数-2023.12.3
题目: 1423. 可获得的最大点数 几张卡牌 排成一行,每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。 每次行动,你可以从行的开头或者末尾拿一张卡牌,最终你必须正好拿 k 张卡牌。 你的点数就是你拿到手中的所有…...

VSCode修改C++版本
新下载了一下VSCode,想使用C17的特性std::optional,但是显示有错误,想想可能是C 版本的问题,查了一下资料,按下面的博客操作,果然解决了。 vscode设置c 版本...

31-WEB漏洞-文件操作之文件包含漏洞全解
31-WEB漏洞-文件操作之文件包含漏洞全解 一、本地包含1.1、无限制包含漏洞文件1.2、有限制包含漏洞文件1.2.1、绕过方法1.2.1.1、%00截断1.2.1.2、长度截断 二、远程包含2.1、无限制包含漏洞文件2.2、有限制包含漏洞文件 三、各种协议流提交流3.1、各协议的利用条件和方法3.1.1…...

预约系统源码解析:打造智能定制化预约服务的技术奇迹
在当今数字化时代,预约系统的重要性日益凸显,而预约系统源码的开放将为各行业带来更加灵活、智能的预约解决方案。本文将深入探讨预约系统源码的技术内幕,为开发者提供实用的代码示例,助力打造智能定制化的预约服务。 技术栈概览…...

关于Maxscript你了解多少?
MAXScript是Autodesk 3dMax的内置脚本语言。MAXScript为3dMax用户提供了以下功能: 编写程序使用的大部分方面的脚本,如建模、动画、材质、渲染等。 通过命令行侦听器窗口以交互方式控制程序。 在自定义实用工具面板卷展栏或无模式窗口中打包脚本&…...
Xshell全局去除提示音
使用Xshell的时候经常会按TAB或者一些操作指令的时候的时候听到提示音,非常的烦 通常来说在Xshell中可以单独修改每一个会话的属性,将提示音关闭,但是新增的会话依然带有提示音,还得一个个的关闭,非常麻烦,…...

JAVA代码优化:Spring中redis的工具类
基于Spring框架和Redis的缓存工具类。该类提供了一系列方法用于操作Redis缓存,包括设置缓存对象、设置缓存超时时间、获取缓存对象、删除对象、缓存List、Set、Map等操作。通过这些方法可以方便地对Redis进行数据缓存和读取操作。同时,该类使用了Spring的…...
MathType 7.5.2中文版软件使用期到了怎么办?
MathType 7.5.2中文版作为一款专业的公式编辑器,MathType受到很多人的青睐,它可以将编辑好的公式保存成多种图片格式或透明图片模式,可以很方便的添加或移除符号、表达式等模板(只需要简单地用鼠标拖进拖出即可),也可以…...

DOM 事件的注册和移除
前端面试大全DOM 事件的注册和移除 🌟经典真题 🌟DOM 注册事件 HTML 元素中注册事件 DOM0 级方式注册事件 DOM2 级方式注册事件 🌟DOM 移除事件 🌟真题解答 🌟总结 🌟经典真题 总结一下 DOM 中如何…...

挖漏洞之SQL注入
(一)漏洞原理 1、 漏洞原理 SQL注入的原理是,是应用系统没有对传递的参数进行过滤,让参数直接拼接到SQL语句中,攻击通过对参数进行篡改,当参数传递到数据库中,逻辑上就会发生变化,就…...

面试篇之微服务(二)
目录 服务容灾 21.什么是服务雪崩? 22.什么是服务熔断?什么是服务降级? 什么是服务熔断? 什么是服务降级? 有哪些熔断降级方案实现? 23.Hystrix怎么实现服务容错? 24.Sentinel怎么实现限…...

java封装详解
/*** Description 封装详解*/ package com.oop;import com.oop.demo04.Student; /*1.提高程序的安全性,保护数据2.隐藏代码的实现细节3.统一接口4.系统可维护增加了*/ public class Application {public static void main(String[] args) {Student s1 new Student(…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
