算法通关第十七关黄金挑战——透析跳跃问题
大家好,我是怒码少年小码。
本篇是贪心思想的跳跃问题专题,跳跃问题出现的频率很高。
跳跃游戏
LeetCode 55:给你一个非负整数数组 nums ,你最初位于数组的 第一个下标。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
- 输入:nums = [2,3,1,1,4]
- 输出:true
- 解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
- 输入:nums = [3,2,1,0,4]
- 输出:false
- 解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
分析:这题的关键是要搞清楚题目的意思。如果当前位置的元素是3,那么你走1/2/3步,最后如果走到的数组中的最后一个位置就算你成功!
注意: 这里很容易就陷入到底具体是跳到哪一步、走多少步的思考漩涡中。这里的关键是能否走到终点。所以我们要尽可能的跳跃到最远的位置,看当前位置最多能覆盖到哪里,如果能覆盖到终点我们就赢了!
如下图:

第一个例子中,3能覆盖{2,1,0},2能覆盖{1,0},1能覆盖{0},而0不能覆盖到4,所以无法达到终点。
可见,第二个例子中有2种跳法{2,1,1,4},{2,3,1,1,4}。
定义一个变量cover表示当前位置可以覆盖的范围,遍历指针只能在cover中的范围变化,每次i变化都要引起cover的变化(cover会得到当前位置i的元素的补充),我们需要找到最远可以到达的位置,也就是需要在cover当前本身的值和补充之后的值之间,取一个最大值。
当cover >= nums.length - 1时,说明可以成功。
public boolean canJump(int[] nums) {if(nums.length == 1){return true;}int cover = 0 ;for(int i = 0 ; i<=cover;i++){cover = Math.max(cover , i+nums[i]);if(cover >= nums.length - 1){return true;}}return false;
}
最短跳跃问题
从上题可以看出一个数组有多种跳跃方式可以到达终点,那么最少需要几步能跳到终点呢?这就是LeetCode 45。
这题我们可以采用:贪心+双指针 的方法解决🤔。
- left用于遍历数组
- steps表示一共跳了多少步
- right表示当前位置能够覆盖的最大范围
maxPosition = Math.max(maxPosition,left + nums[left]);这个还是最远能跳到哪里。当left == right说明当前区间最大覆盖区间已经寻找完毕。
例如上面的第一个例子:


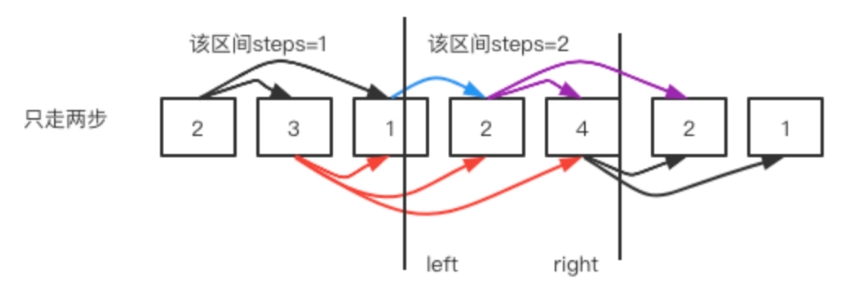
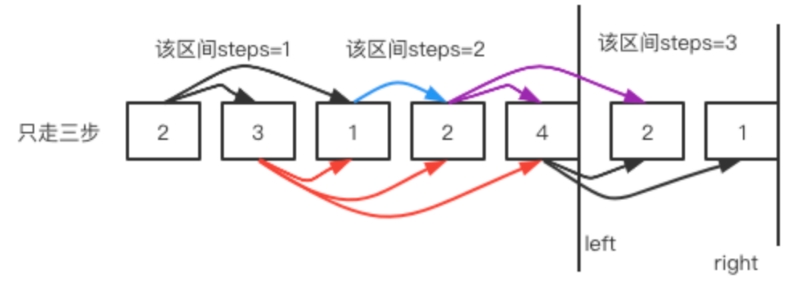
public int jump(int[] nums) {int right = 0 ;int steps = 0 ;int maxPosition = 0;for(int left = 0 ; left < nums.length - 1; left++){//最远能跳到哪里maxPosition = Math.max(maxPosition,left + nums[left]);if(left == right){ //left遍历到了边界,就更新边界并且步数加一right = maxPosition;steps++;}//right指针到了数组的最后if(right >= nums.length - 1){return steps;}}return steps;
}
END
今天这篇都是力扣上的中等难度,在面试的时候也挺常见的,多练练动手敲😎。
相关文章:

算法通关第十七关黄金挑战——透析跳跃问题
大家好,我是怒码少年小码。 本篇是贪心思想的跳跃问题专题,跳跃问题出现的频率很高。 跳跃游戏 LeetCode 55:给你一个非负整数数组 nums ,你最初位于数组的 第一个下标。数组中的每个元素代表你在该位置可以跳跃的最大长度。 …...
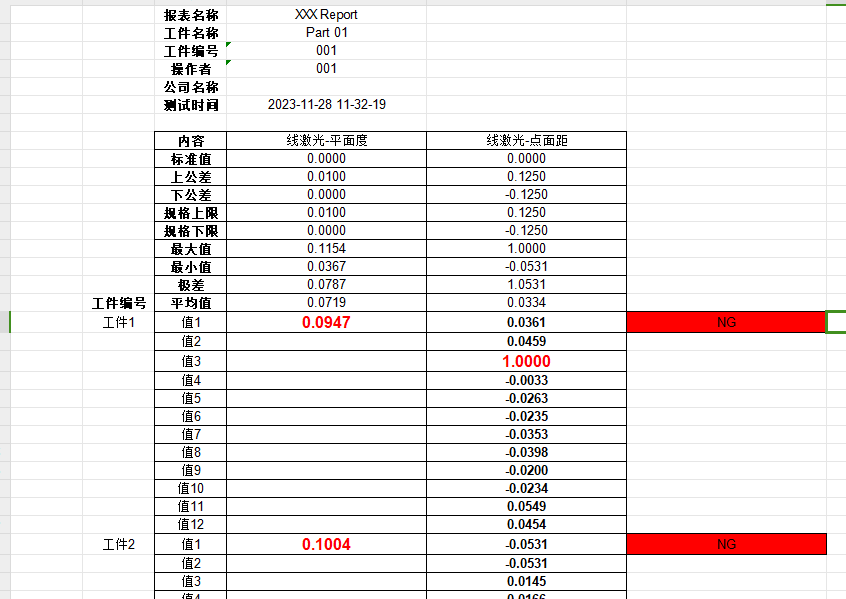
GPT带我学Openpyxl操作Excel
注:以下文字大部分文字和代码由GPT生成 一、openpyxl详细介绍 Openpyxl是一个用于读取和编写Excel 2010 xlsx/xlsm/xltx/xltm文件的Python库。它允许您使用Python操作Excel文件,包括创建新的工作簿、读取和修改现有工作簿中的数据、设置单元格格式以及编…...

图扑参展高交会-全球清洁能源创新博览会
“相聚鹏城深圳,共享能源盛宴” 第二十五届中国国际高新技术成果交易会(简称“高交会”)于 11 月 15-18 日在深圳盛大开幕。高交会由商务部、科学技术部、工业和信息化部、国家发展改革委、农业农村部、国家知识产权局、中国科学院、中国工程院和深圳市人民政府共同…...

vue v-permission权限指令
控制页面及按钮的显示隐藏 src/directive/permission/index.js import permission from ./permissionconst install function(Vue) {Vue.directive(permission, permission) }if (window.Vue) {window[permission] permissionVue.use(install); // eslint-disable-line }per…...

ER图是什么,怎么画?
ER图(Entity-Relationship Diagram)是一种用于描述实体间关系的图形化表示方法。它主要用于数据库设计,可以清晰地展示实体、属性和实体间的联系。常用的ER图类型包括: 实体-关系模型(Entity-Relationship Model&…...

基于51单片机的十字路口交通灯_5s黄灯倒计时闪烁
基于51单片机十字路口交通灯_5s黄灯闪烁 (程序仿真仿真视频) 仿真:proteus 7.8 程序编译器:keil 4/keil 5 编程语言:C语言 设计编号:J006 功能要求 交通灯运行状态: (1&…...

JavaWeb | JSP内置对象
目录: 1.认识JSP内置对象2.JSP内置对象的特点3.九大内置对象3.1 out对象的作用向 “客户端” 输出各种数据内容对 “服务器” 上的输出缓冲区进行管理 3.2 request对象的作用能够获取客户端的基本信息 3.3 response对象的作用利用response对象进行 “重定向”利用re…...
如何保持高能量
精力管理 精力管理对于平衡多项任务和保持热情至关重要。 通过自我积极反馈循环系统培养积极的内心声音。 培养仪式和习惯来控制内心的声音并保持能量。 学习语言带来正能量和宝贵的技能 保持高能量需要自我赋权和体力充电。 经常锻炼有很多好处,包括改善健康…...

Oracle研学-基础操作
学自B站黑马程序员笔记 一 创建表空间(创建数据文件) 创建表空间同时会创建一个数据文件(下面5行应该是一句话),表空间在PLSQL的Object的tablespace中可以看到 create tablespace waterboss //创建表空间 datafile c:\waterboss.dbf //创建表空间对应的…...

jmeter下载地址
Jmeter安装教程【5.5】【Windows】jmeter详细安装配置教程,装不好你打我_一只莽夫的博客-CSDN博客...

C语言,求取数组的序亏:已知一个整数数组,求出个数组中每个元素在整个 数组的排序。
要求获取整数数组中每个元素的排序,可以使用以下方法: 1. 定义一个结构体数组,其中每个结构体包含数组元素的值和索引。 2. 遍历整数数组,将每个元素与其索引一起存储到结构体数组中。 3. 对结构体数组进行排序,按照…...

信息流广告行为兴趣定向底层逻辑算法
行为兴趣定向 1: 行为兴趣的背后是计划的数据 行为是用户在平台的动作:点赞、评论、分享、点击、下单、成交等,用户发生过的标签 兴趣不一定发生,我有打高尔夫的兴趣,但是从来没打过,因为穷 系统会根据用户的行为标…...

Selenium——isDisplayed()、isEnabled()、isSelected()
判断页面是否存在某元素 Selenium没有直接提供判断是否存在的方法,可以使用findElements返回的数量判断;或者判断findElement是否抛出异常 webDriver.findElements(By.xpath("(//div[classel-button-group]//button)[1]")).size()isDisplaye…...

unity UGUI中获取点击位置处的URL链接
需求是,我们在一个text组件中像写网页那样写入链接,然后点击这个链接,就能访问配置的网页啥的。比如: <a href"hello">链接文本</a></summary> 最终的效果如下: 图中,image区…...

【Arduino库之:FastLED库】
第一:基础 led [ 0 ] CRGB::Red; //为第一个灯珠设置红色 FastLED.show(); //这个作用才会显示 示例程序: #include <FastLED.h> #define NUM_LEDS 8 #define DATA_PIN 7 #define CLOCK_PIN 13 CRGB leds[NUM_LEDS]; CRGB myGRBcolor(0…...
两道面试题秒杀你的C++基础!
大家好,我是光城,今天发两个非常重要的面试题,可以留言区说出你的答案,这两个题目都比较重要,看你能答对不? 1.C中初始化变量有几种方式,各自有什么区别? 或者说Initialization分为哪…...
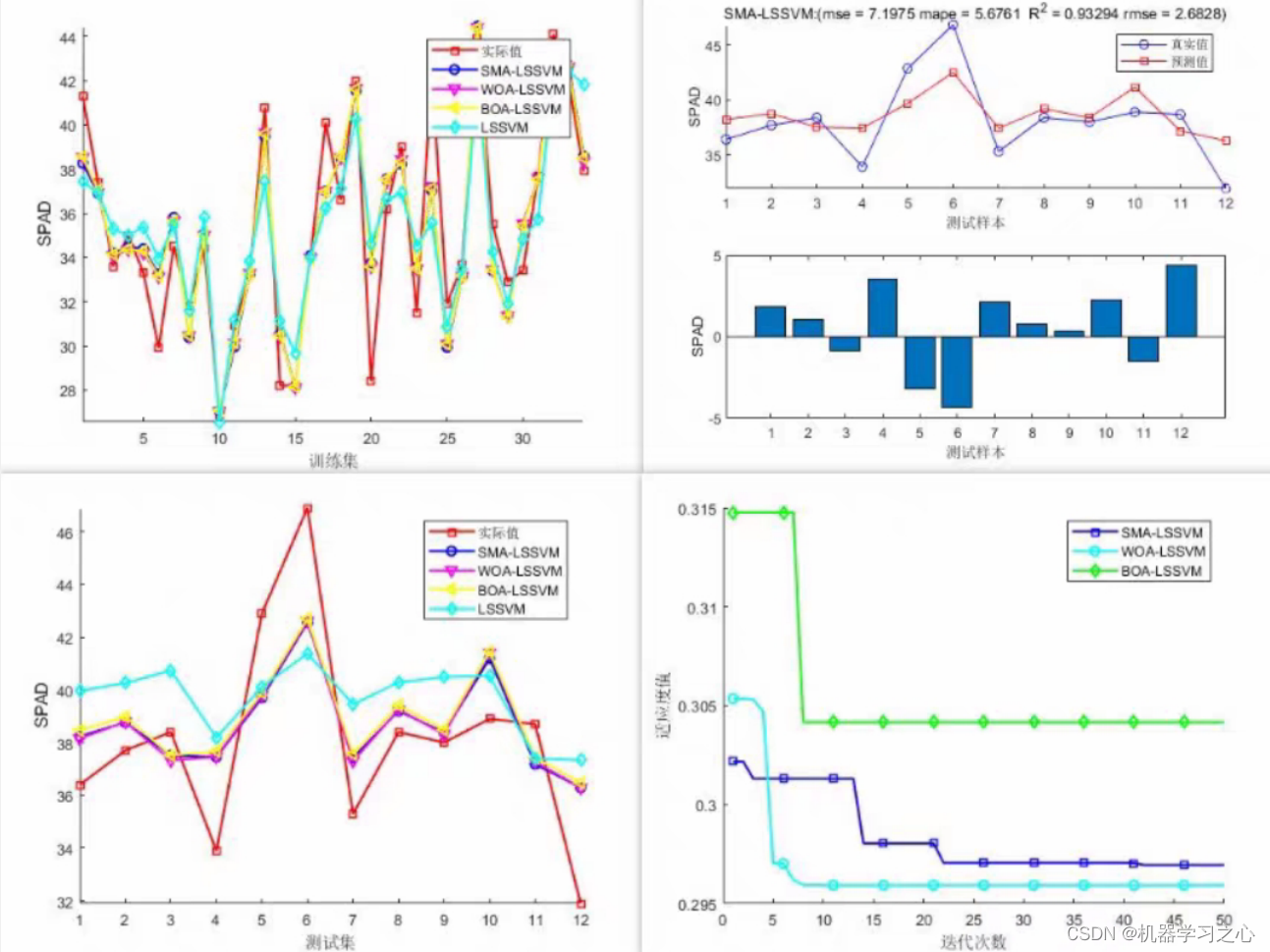
回归预测 | MATLAB实现SMA+WOA+BOA-LSSVM基于黏菌算法+鲸鱼算法+蝴蝶算法优化LSSVM回归预测
回归预测 | MATLAB实现SMAWOABOA-LSSVM基于黏菌算法鲸鱼算法蝴蝶算法优化LSSVM回归预测 目录 回归预测 | MATLAB实现SMAWOABOA-LSSVM基于黏菌算法鲸鱼算法蝴蝶算法优化LSSVM回归预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 MATLAB实现SMAWOABOA-LSSVM基于黏菌算法…...
在C语言中的应用)
柔性数组(Flexible Array Members)在C语言中的应用
什么是柔性数组? 在C语言中,柔性数组(Flexible Array Members,FAMs)是C99标凈引入的一种便捷的数据结构,用于声明具有可变大小数组的结构体。柔性数组通常用于当结构体的大小在编译时不确定,但…...
华为手环配置技巧
前言 华为手环作为生活健康辅助设备发挥不可忽视的作用,但每次更换手环后需要重新配置。华为手环不仅有健康监测、消息通知、天气推送、离线支付、公交卡、运动锻炼、等功能,还有倒计时、计时器、手电筒、闹钟、等小工具。下文介绍如何进行配置。 配置…...

2023全球数字贸易大赛--什么是 DID 身份,中青校园APP,全球碳交易=树根格致,多元空间=购物时代的web3.0,超喵Overview
目录 什么是 DID 身份,为什么需要 DID 1. 中心化身份的问题 2. 为什么 DID 一定会出现...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
