洛谷 P2984 [USACO10FEB] Chocolate Giving S
文章目录
- [USACO10FEB] Chocolate Giving S
- 题面翻译
- 题目描述
- 输入格式
- 输出格式
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 题意解析
- CODE
- 给点思考
[USACO10FEB] Chocolate Giving S
题面翻译
题目链接:https://www.luogu.com.cn/problem/P2984
题目描述
FJ 有 B B B 头奶牛 ( 1 ≤ B ≤ 25000 ) (1\le B\le 25000) (1≤B≤25000),有 N ( 2 × B ≤ N ≤ 50000 ) N(2\times B\le N\le 50000) N(2×B≤N≤50000) 个农场,编号 1 1 1 到 N N N,有 M ( N − 1 ≤ M ≤ 100000 ) M(N-1\le M\le 100000) M(N−1≤M≤100000) 条双向边,第 i i i 条边连接农场 R i R_i Ri 和 S i ( 1 ≤ R i ≤ N , 1 ≤ S i ≤ N ) S_i(1\le R_i\le N, 1\le S_i\le N) Si(1≤Ri≤N,1≤Si≤N),该边的长度是 L i ( 1 ≤ L i ≤ 2000 ) L_i(1\le L_i\le 2000) Li(1≤Li≤2000)。居住在农场 P i P_i Pi 的奶牛 A ( 1 ≤ P i ≤ N ) (1\le P_i\le N) (1≤Pi≤N),想送一份新年礼物给居住在农场 Q i ( 1 ≤ Q i ≤ N ) Q_i(1\le Q_i\le N) Qi(1≤Qi≤N) 的奶牛 B,但是奶牛 A 必须先到 FJ(居住在编号 1 1 1 的农场)那里取礼物,然后再送给奶牛 B。你的任务是:奶牛 A 至少需要走多远的路程?
输入格式
-
第一行三个整数 N , M , B N,M,B N,M,B。
-
第 2 2 2 至 M + 1 M+1 M+1 行,每行 3 3 3 个整数 R i , S i , L i R_i,S_i,L_i Ri,Si,Li。
-
第 M + 2 M+2 M+2 至 M + B + 1 M+B+1 M+B+1 行,进行 B B B 次询问,每行 2 2 2 个整数 P i , Q i P_i ,Q_i Pi,Qi。
输出格式
每次询问输出一个整数,即答案。
题目描述
Farmer John is distributing chocolates at the barn for Valentine’s day, and B (1 <= B <= 25,000) of his bulls have a special cow in mind to receive a chocolate gift.
Each of the bulls and cows is grazing alone in one of the farm’s N (2*B <= N <= 50,000) pastures conveniently numbered 1…N and connected by M (N-1 <= M <= 100,000) bidirectional cowpaths of various lengths. Some pastures might be directly connected by more than one cowpath. Cowpath i connects pastures R_i and S_i (1 <= R_i <= N; 1 <= S_i <= N) and has length L_i (1 <= L_i <= 2,000).
Bull i resides in pasture P_i (1 <= P_i <= N) and wishes to give a chocolate to the cow in pasture Q_i (1 <= Q_i <= N).
Help the bulls find the shortest path from their current pasture to the barn (which is located at pasture 1) and then onward to the pasture where their special cow is grazing. The barn connects, one way or another (potentially via other cowpaths and pastures) to every pasture.
As an example, consider a farm with 6 pastures, 6 paths, and 3 bulls (in pastures 2, 3, and 5) who wish to bestow chocolates on their love-objects:
*1 <-- Bull wants chocolates for pasture 1 cow[4]--3--[5] <-- [5] is the pasture ID/ |/ |4 2 <-- 2 is the cowpath length/ | between [3] and [4][1]--1--[3]*6/ \ /9 3 2/ \/[6] [2]*4
* The Bull in pasture 2 can travel distance 3 (two different ways) to get to the barn then travel distance 2+1 to pastures [3] and [4] to gift his chocolate. That’s 6 altogether.
* The Bull in pasture 5 can travel to pasture 4 (distance 3), then pastures 3 and 1 (total: 3 + 2 + 1 = 6) to bestow his chocolate offer.
* The Bull in pasture 3 can travel distance 1 to pasture 1 and then take his chocolate 9 more to pasture 6, a total distance of 10.
输入格式
* Line 1: Three space separated integers: N, M, and B
* Lines 2…M+1: Line i+1 describes cowpath i with three
space-separated integers: R_i, S_i, and L_i
* Lines M+2…M+B+1: Line M+i+1 contains two space separated integers: P_i and Q_i
输出格式
* Lines 1…B: Line i should contain a single integer, the smallest distance that the bull in pasture P_i must travel to get chocolates from the barn and then award them to the cow of his dreams in pasture Q_i
样例 #1
样例输入 #1
6 7 3
1 2 3
5 4 3
3 1 1
6 1 9
3 4 2
1 4 4
3 2 2
2 4
5 1
3 6
样例输出 #1
6
6
10
题意解析
- 找一个点先到 1 1 1 号点的最短距离,再找 1 1 1 号点到另一点的最短距离,求两者之和。
- 乍一看以为是 F l o y d Floyd Floyd 算法,但是一看数据范围很大,那就并不是了,那还有什么算法能解决这种最短路问题呢?
- 其实这并不是多源最短路问题,因为是双向图,所以你到我的最短路其实也是我到你的最短路,所以这题就变成了 1 1 1 号点到另外两个点的最短路之和的问题了,其实是单源最短路问题。
- 考虑到 D i j k s t r a Dijkstra Dijkstra 可能超时,所以用 S P F A SPFA SPFA
CODE
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#define ll long long
#define INF 0x3f3f3f3f using namespace std;typedef pair<int, int> pii;const int N = 50050, M = 2e5 + 10;
int h[N], e[M], ne[M], w[M], idx; // 定义图的存储结构
int dist[N]; // 存储每个节点到源点的最短距离
bool st[N]; // 存储每个节点是否在队列中
int n, m, b; // n是节点数,m是边的数目,b是查询的数目// 添加一条边
void add(int a, int b, int c){e[idx] = b; // 边的终点ne[idx] = h[a]; // 下一条相同起点的边w[idx] = c; // 边的权重h[a] = idx++; // 更新起点a的最后一条边
}// SPFA算法,用于求解单源最短路径
void spfa(){memset(dist, INF, sizeof dist); // 初始化所有节点到源点的距离为无穷大dist[1] = 0; // 源点到自己的距离为0queue<int> q;q.push(1); // 将源点加入队列st[1] = true; // 标记源点已经在队列中while(q.size()){auto t = q.front(); // 取出队首元素q.pop();st[t] = false; // 标记t已经不在队列中for(int i = h[t]; i != -1; i = ne[i]){ // 遍历所有从t出发的边int j = e[i];if(dist[j] > dist[t] + w[i]){ // 如果可以通过t到j的距离小于当前的最短距离dist[j] = dist[t] + w[i]; // 更新最短距离if(!st[j]){ // 如果j不在队列中q.push(j); // 将j加入队列st[j] = true; // 标记j已经在队列中}}}}
}int main()
{memset(h, -1, sizeof h); // 初始化邻接表cin >> n >> m >> b; // 输入节点数,边的数目,查询的数目while(m--){int a, b, c;scanf("%d%d%d", &a, &b, &c); // 输入边的信息add(a, b, c), add(b, a, c); // 将边添加到图中}spfa(); // 执行SPFA算法,求解最短路径while(b--){int p, q;scanf("%d%d", &p, &q); // 输入查询cout << dist[p] + dist[q] << endl; // 输出结果}
}给点思考
- 为什么边权数组不用初始化为 I N F INF INF:
- 因为只有在遍历队列首元素
t的所有出边时才会用到w[i],所以能用到肯定存在,所以不需要初始化。
- 因为只有在遍历队列首元素
- 无向图该注意的问题:
- 边数应该开两倍,因为无向,开少了就
RE。
- 边数应该开两倍,因为无向,开少了就
相关文章:

洛谷 P2984 [USACO10FEB] Chocolate Giving S
文章目录 [USACO10FEB] Chocolate Giving S题面翻译题目描述输入格式输出格式 题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 题意解析CODE给点思考 [USACO10FEB] Chocolate Giving S 题面翻译 题目链接:https://www.luogu.com.cn/problem/P2984 题目描…...

【专题】【数列极限】
【整体思路】 【常用不等式】...

oracle基础系统学习文章目录
oracle基础系统学习——点击标题可跳转对应文章 01.CentOS7静默安装oracle11g 02.Oracle的启动过程 03.从简单的sql开始 04.Oracle的体系架构 05.Oracle数据库对象 06.Oracle数据备份与恢复 07.用户和权限管理 08.Oracle的表 09.Oracle表的分区 10.Oracle的同义词与序列 11.Or…...
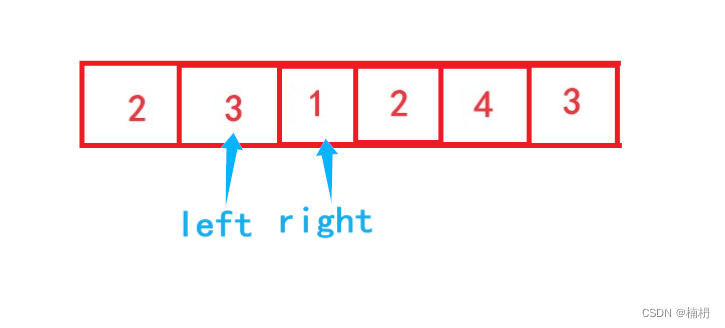
长度最小的子数组(Java详解)
目录 题目描述 题解 思路分析 暴力枚举代码 滑动窗口代码 题目描述 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条…...

计算机组成学习-数据的表示和运算总结
复习本章时,思考以下问题: 1)在计算机中,为什么要采用二进制来表示数据?2)计算机在字长足够的情况下能够精确地表示每个数吗?若不能,请举例说明。3)字长相同的情况下,浮点数和定点数的表示范围…...
(八))
目标检测YOLO系列从入门到精通技术详解100篇-【目标检测】机器视觉(基础篇)(八)
目录 前言 知识储备 机器视觉学习路线 视觉算法流程...

【4】基于多设计模式下的同步异步日志系统-框架设计
7. 日志系统框架设计 本项⽬实现的是⼀个多日志器日志系统,主要实现的功能是让程序员能够轻松的将程序运行日志信息落地到指定的位置,且⽀持同步与异步两种方式的日志落地方式。 项目的框架设计将项目分为以下几个模块来实现。 日志等级模块 日志等级模…...
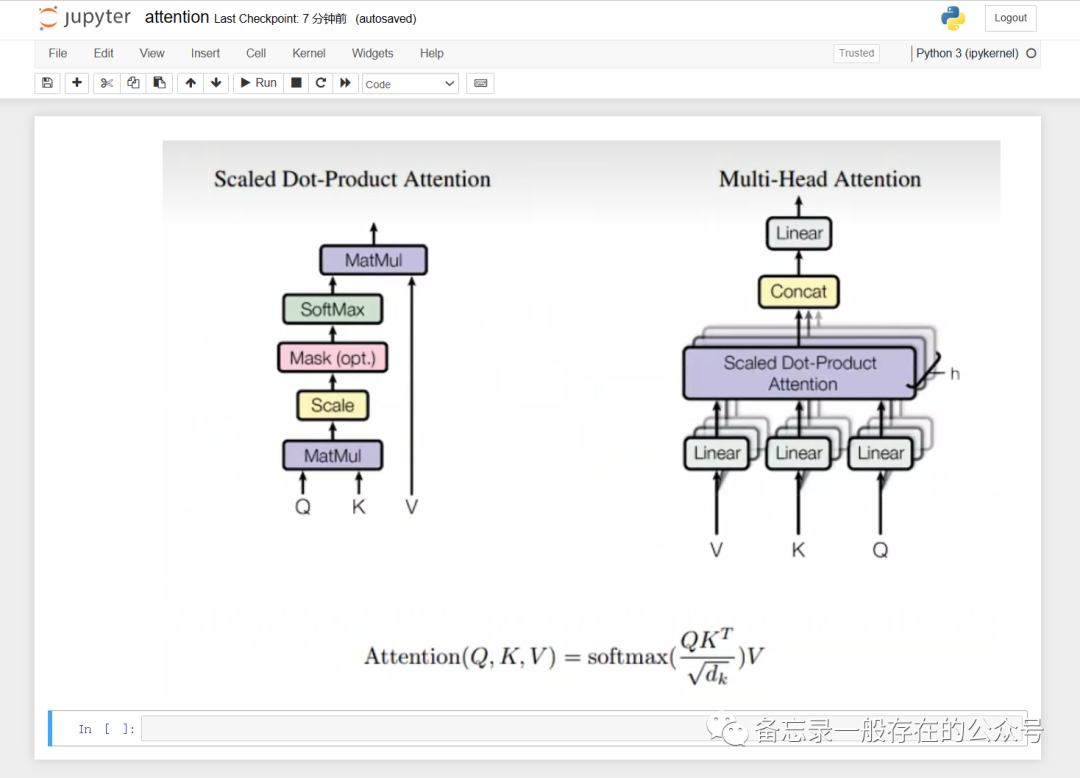
Jupyter Markdown 插入图片
首先截图 注意 这一步是关键的!! 它需要使用电脑自带的截图,用qq啊vx啊美图秀秀那些都不行哦。 截图之后复制: 然后快捷键粘贴到jupyter里面,它会生成一段代码(没有代码就是说截图形式不对)&a…...
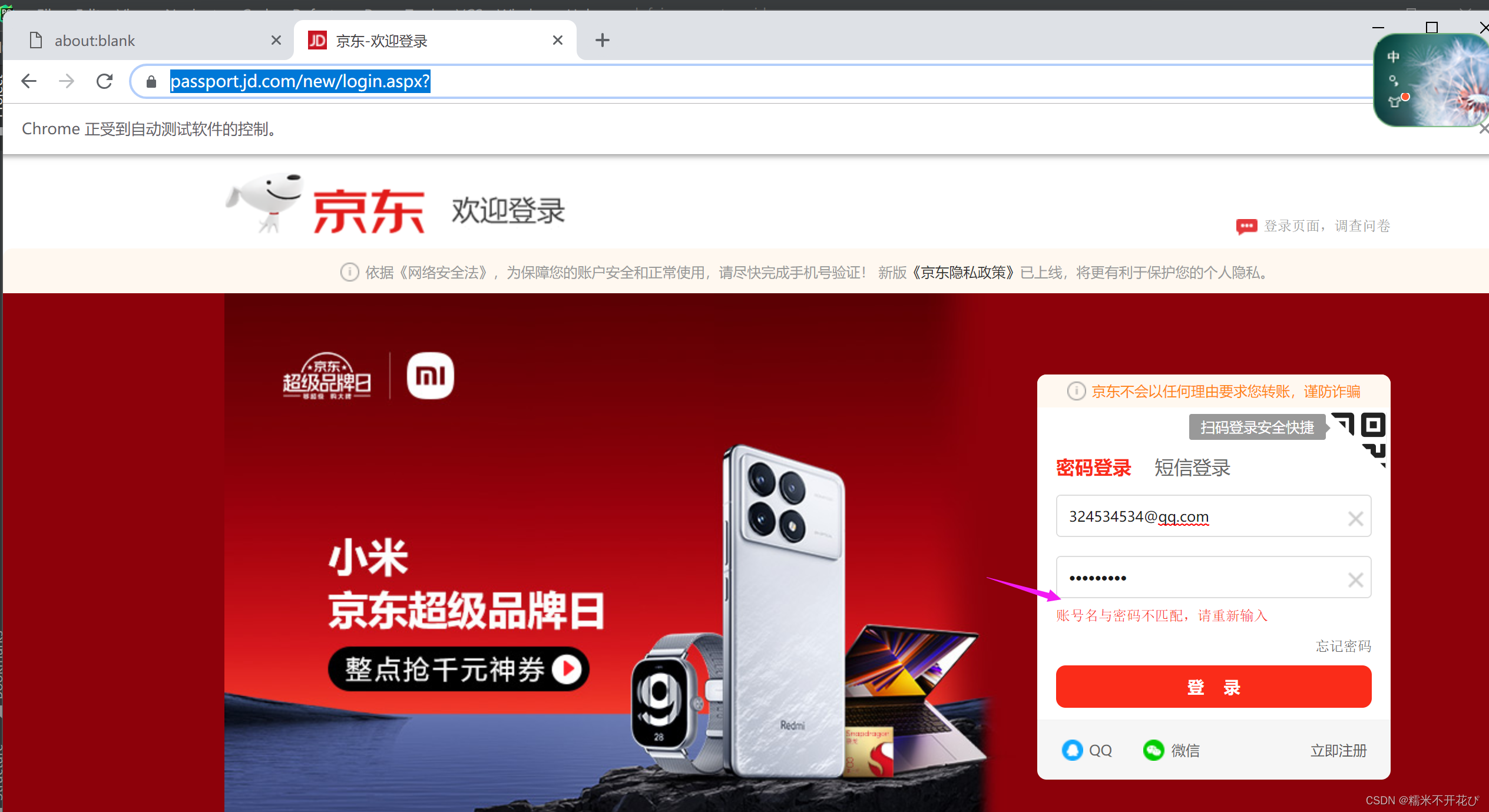
web自动化 -- pyppeteer
由于Selenium流行已久,现在稍微有点反爬的网站都会对selenium和webdriver进行识别,网站只需要在前端js添加一下判断脚本,很容易就可以判断出是真人访问还是webdriver。虽然也可以通过中间代理的方式进行js注入屏蔽webdriver检测,但…...
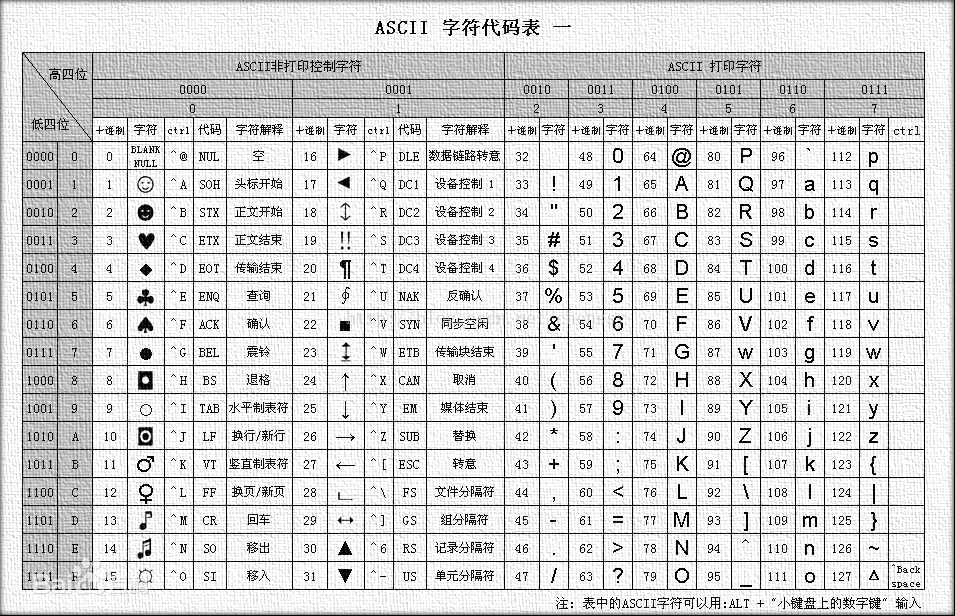
Java 数组另类用法(字符来当数组下标使用)
一、原因 看力扣的时候发现有位大佬使用字符来当数组下标使用。 class Solution {public int lengthOfLongestSubstring(String s) {int result 0;int[] hash new int[130];int i 0;for(int j 0; j < s.length(); j) {while(hash[s.charAt(j)] > 0) {hash[s.charAt…...

error转string
1 概述 在golang中,error类型是非常常见的一种数据类型。在开发过程中,经常会遇到需要将error类型转换成string类型的情况。本文主要介绍几种常见的golang error转string的方法。 2 使用Error()函数 在golang中,Error()函数是error类型的一…...

Android监听用户的截屏、投屏、录屏行为
Android监听用户的截屏、投屏、录屏行为 一.截屏 方案一:使用系统广播监听截屏操作 从Android Q(10.0)开始,Intent.ACTION_SCREEN_CAPTURED_CHANGED字段不再被支持。这是因为Google在安卓10 中引入了一个新的隐私限制&#…...

MATLAB算法实战应用案例精讲-【路径规划】 图搜索算法
目录 前言 几个高频面试题目 运动规划、路径规划、轨迹规划对比 1. 运动规划 2. 路径规划VS轨迹规划...

Elasticsearch-Kibana使用教程
1.索引操作 1.1创建索引 PUT /employee {"settings": {"index": {"refresh_interval": "1s","number_of_shards": 1,"max_result_window": "10000","number_of_replicas": 0}},"mappi…...
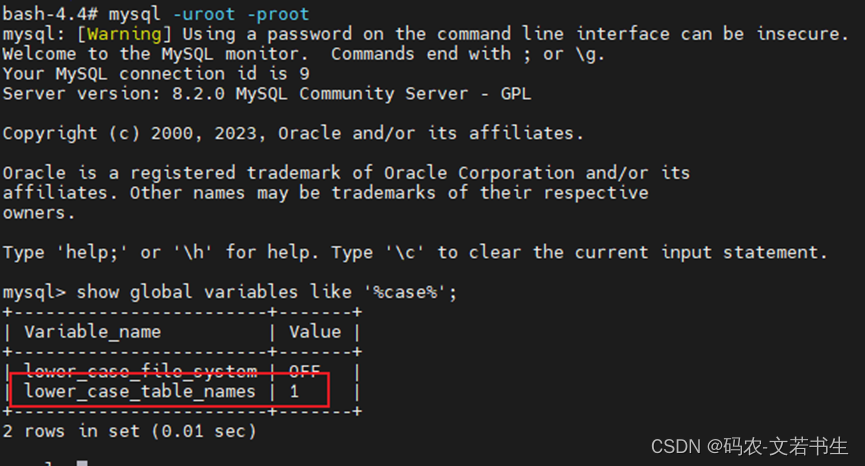
mysql(八)docker版Mysql8.x设置大小写忽略
Mysql 5.7设置大小写忽略可以登录到Docker内部,修改/etc/my.cnf添加lower_case_table_names1,并重启docker使之忽略大小写。但MySQL8.0后不允许这样,官方文档记录: lower_case_table_names can only be configured when initializ…...

KALI LINUX攻击与渗透测试
预计更新 第一章 入门 1.1 什么是Kali Linux? 1.2 安装Kali Linux 1.3 Kali Linux桌面环境介绍 1.4 基本命令和工具 第二章 信息收集 1.1 网络扫描 1.2 端口扫描 1.3 漏洞扫描 1.4 社交工程学 第三章 攻击和渗透测试 1.1 密码破解 1.2 暴力破解 1.3 漏洞利用 1.4 …...
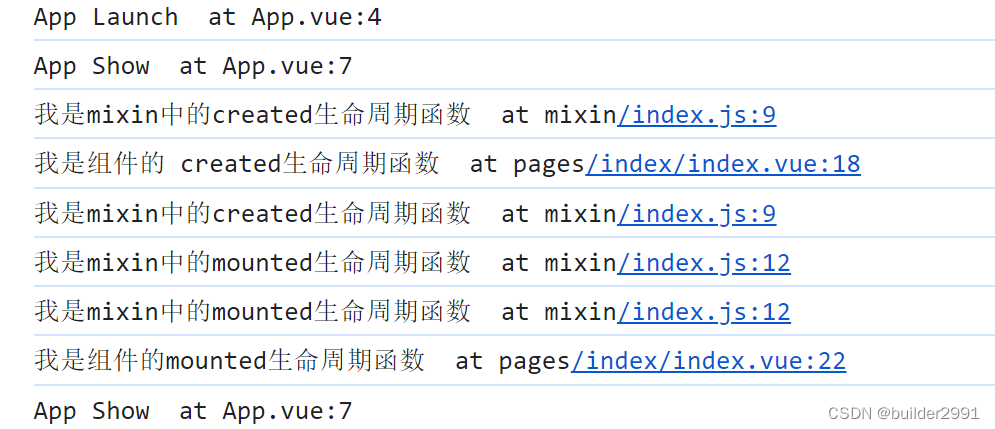
vue之mixin混入
vue之mixin混入 mixin是什么? 官方的解释: 混入 (mixin) 提供了一种非常灵活的方式,来分发 Vue 组件中的可复用功能。一个混入对象可以包含任意组件选项。当组件使用混入对象时,所有混入对象的选项将被“混合”进入该组件本身的…...

[ffmpeg] find 编码器
背景 整理 ffmpeg 中,如何通过名字或者 id 找到对应编码器的。 具体流程 搜索函数 avcodec_find_encoder // 通过 ID 搜索编码器 avcodec_find_encoder_by_name // 通过名字搜索编码器源码分析 ffmpeg 中所有支持的编码器都会注册到 codec_list.c 文件中&…...

Android CardView基础使用
目录 一、CardView 1.1 导入material库 1.2 属性 二、使用(效果) 2.1 圆角卡片效果 2.2 阴影卡片效果 2.3 背景 2.3.1 设置卡片背景(app:cardBackgroundColor) 2.3.2 内嵌布局,给布局设置背景色 2.4 进阶版 2.4.1 带透明度 2.4.2 无透明度 一、CardView 顾名…...

云原生Kubernetes系列 | init container初始化容器的作用
云原生Kubernetes系列 | init container初始化容器的作用 kubernetes 1.3版本引入了init container初始化容器特性。主要用于在启动应用容器(app container)前来启动一个或多个初始化容器,作为应用容器的一个基础。只有init container运行正常后,app container才会正常运行…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
