初识动态规划算法(题目加解析)
文章目录
- 什么是动态规划
- 正文
- 力扣题
- 第 N 个泰波那契数
- 三步问题
- 使用最小花费爬楼梯
- 总结
什么是动态规划
线性动态规划:是可以用一个dp表来存储内容,并且找到规律存储,按照规律存储。让第i个位置的值等于题目要求的答案
>dp表:dp表就是用一个连续的空间存储需要存储的有规律的值。
干说无力直接正文
正文
力扣题
第 N 个泰波那契数
题目:地址
题目解析:

给定了三个数 T0,T1,T2
求Tn的值
**根据题意可以翻译成 Tn = Tn-1+Tn-2+Tn-**3
动态规则的题目都可以分五步
1、状态表示(★)
状态表示是必须要会的并且理解的
>一般的状态表示是:经验+题目解析
经验是要多写才能得出来的
这个题目的状态表示已经给出来了
Tn的值是前三个值的合
2、状态转移方程(★)
状态转移方程一般可以表示成 第n个值=····
题目已经给出Tn=Tn-1+Tn-2+Tn-3
3、初始化
把dp表初始化成0
4、填dp表顺序
从左往右填
5、返回值
dp[n]
代码答案:
class Solution {
public:int tribonacci(int n) {if(n==0){return 0;}if(n==1||n==2){return 1;}// vector<int> dp(n+1);// dp[0]=0,dp[1]=1,dp[2]=1;// for(int i =3;i<=n;i++)// {// dp[i]=dp[i-1]+dp[i-2]+dp[i-3];// }//空间优化int a= 0,b=1,c=1,d=0;for(int i =3;i<=n;i++){d=a+b+c;a=b;b=c;c=d;}return d;}
};
三步问题
题目:地址
题目解析:

题目解释:
这个小男孩一小子可以走 1层/2层/3层
走到第n层的时候有多少种方法
如果结果太大需要%1000000007
动态规划的五步走:
1、状态表示(★)
这个题目的状态表示是
2、状态转移方程(★)
依照上面的解释
动态方程为Tn = Tn-1+Tn-2+Tn-3
3、初始化
初始化dp表为0
4、存储dp表的顺序
从左往右
5、返回值
dp[n]
代码:
class Solution {
public:int waysToStep(int n) {if(n==1||n==2){return n;}if(n==3){return 4;}// vector<int> dp(n+1);// dp[1] = 1,dp[2]=2,dp[3]=4;//空间优化int a =1,b=2,c=4,d=0;for(int i = 4 ;i<=n;i++){//dp[i]=((dp[i-1]+dp[i-2])%1000000007+dp[i-3])%1000000007;d=((a+b)%1000000007+c)%1000000007;a=b;b=c;c=d;}return d;}
};
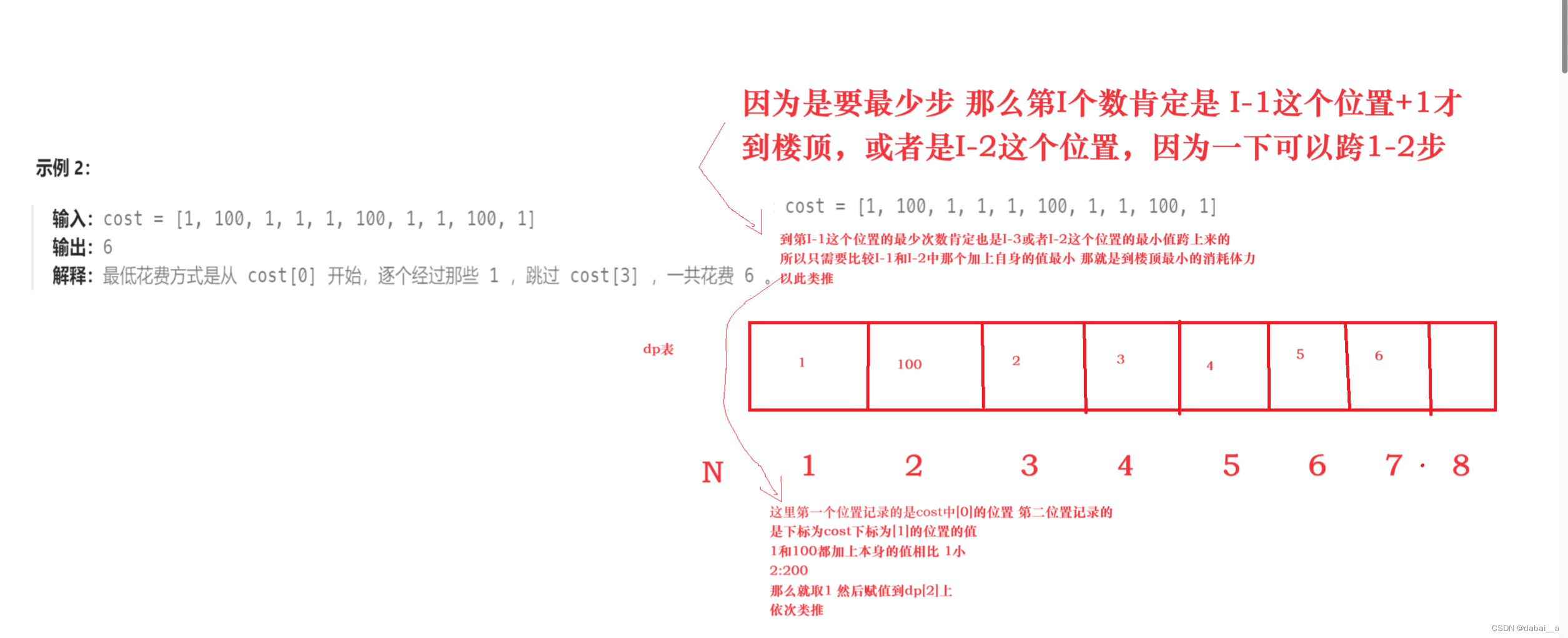
使用最小花费爬楼梯
题目:地址
题目解析:

题目解释:
一个人一下可以走1-2步
最少需要花费多少体力到楼顶
这里的楼顶不是传过来的字符串的位置
因为如果是传过来的字符串的位置那么应该不用+他的值
但是用例1来说
10直接2步到10应该是最快的
但是解释是15
所以楼顶的位置应该在传过来字符的后一个位置
五步走:
1、状态表示
2、状态转移方程
方程是:dp[i]=min(cost[i-1]+dp[i-1],cost[i-2]+dp[i-2])
3、初始化
把dp表初始化
4、存入dp表的位置
从做向右
5、返回值
返回dp[i]位置的值
代码:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size()+2);for(int i =2;i<=cost.size();i++){dp[i]=min(cost[i-1]+dp[i-1],cost[i-2]+dp[i-2]);}return dp[cost.size()];}
};
总结
这三个题的是类似的
都是用前几个数来对比或者相加
可能在解释的时候有些不好理解,作者也是刚学不久,分享一下自己的看法,喜欢的可以点点赞。
相关文章:
初识动态规划算法(题目加解析)
文章目录 什么是动态规划正文力扣题第 N 个泰波那契数三步问题使用最小花费爬楼梯 总结 什么是动态规划 线性动态规划:是可以用一个dp表来存储内容,并且找到规律存储,按照规律存储。让第i个位置的值等于题目要求的答案 >dp表:dp表就是用一…...
Vue2.0与Vue3.0的区别
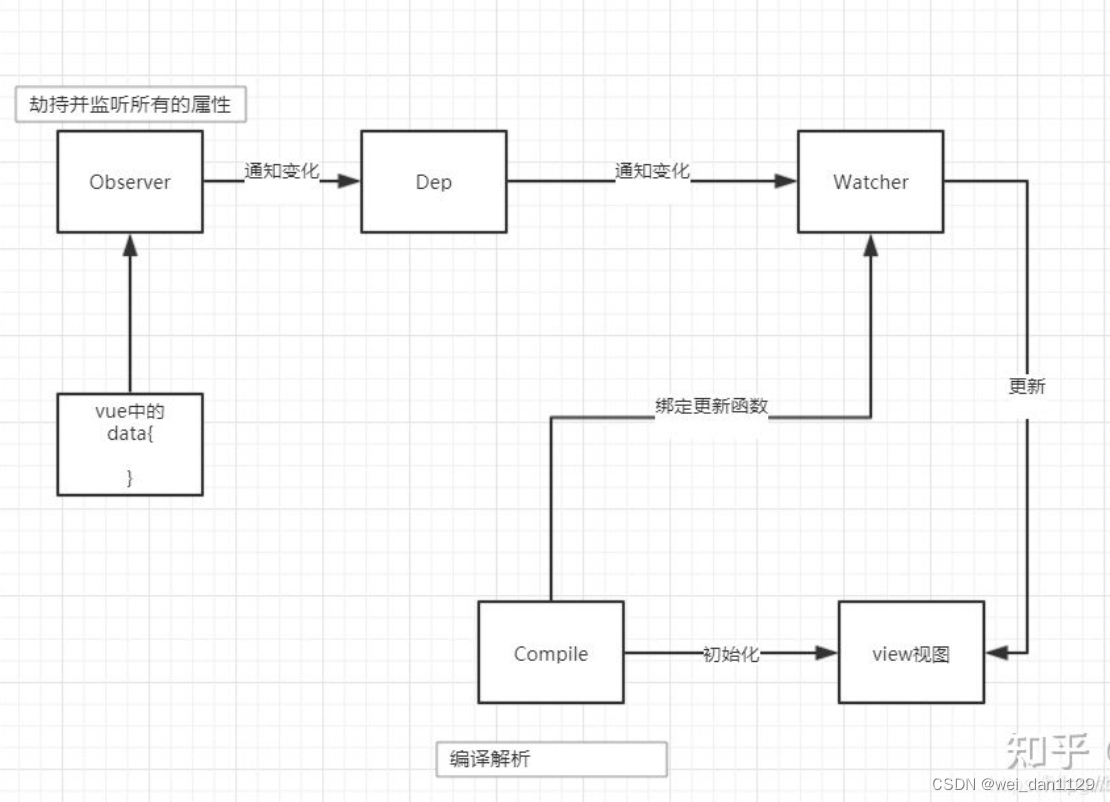
一、Vue2和Vue3的数据双向绑定原理发生了改变 Vue2的双向数据绑定是利用ES5的一个API,Object.definePropert()对数据进行劫持 结合 发布 订阅模式的方式来实现的。通过Object.defineProperty来劫持数据的setter,getter,在数据变动时发布消息…...

探索人工智能领域——每日20个名词详解【day6】
目录 前言 正文 总结 🌈嗨!我是Filotimo__🌈。很高兴与大家相识,希望我的博客能对你有所帮助。 💡本文由Filotimo__✍️原创,首发于CSDN📚。 📣如需转载,请事先与我联系以…...
C++初阶 | [七] string类(上)
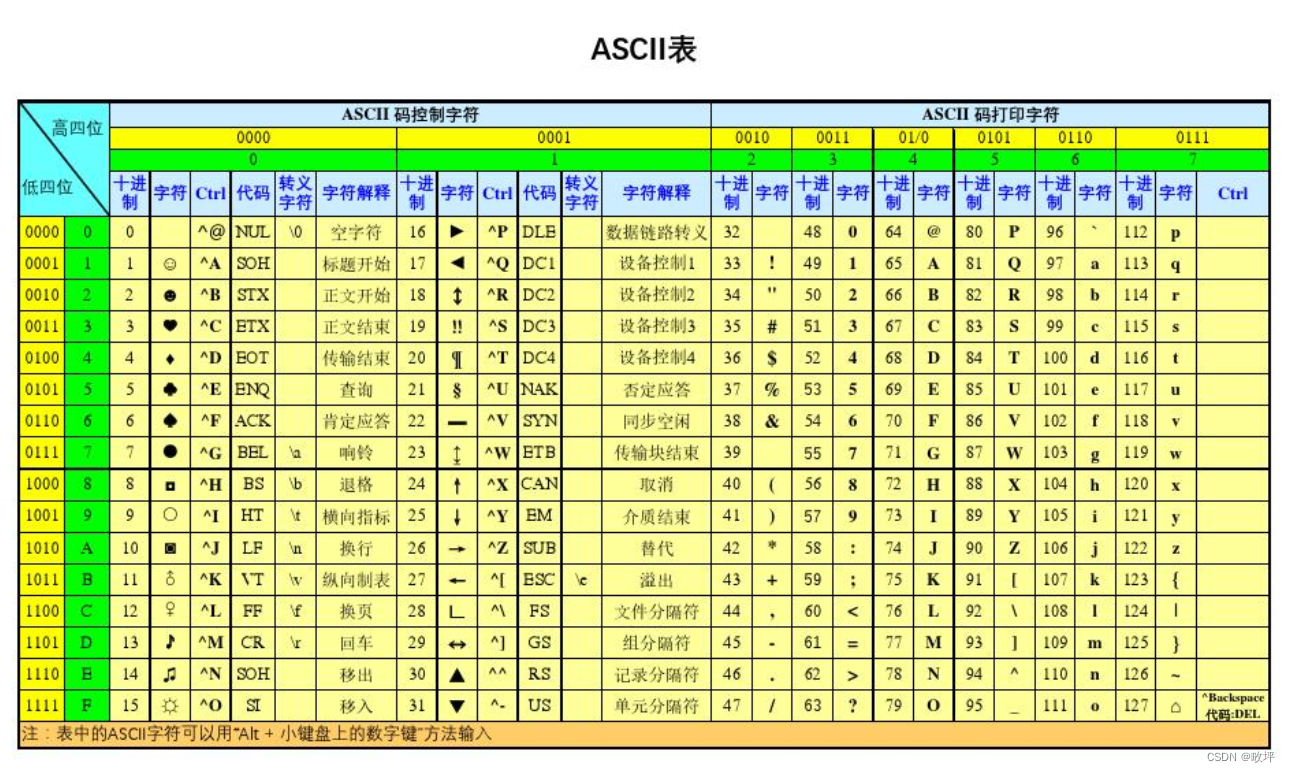
摘要:标准库中的string类的常用函数 C语言中,字符串是以\0结尾的一些字符的集合,为了操作方便,C标准库中提供了一些str系列的库函数, 但是这些库函数与字符串是分离开的,不太符合OOP(面向对象)的思想&#…...
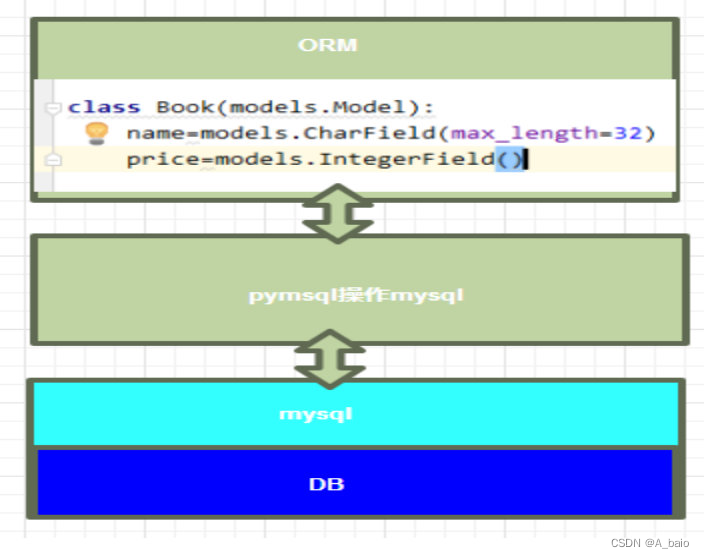
Django总结
文章目录 一、Web应用Web应用程序的优点Web应用程序的缺点应用程序有两种模式C/S、B/S C/S 客户端/服务端局域网连接其他电脑的MySQL数据库1.先用其他电脑再cmd命令行ping本机ip2.开放MySQL的访问 B/S 浏览器/服务端基于socket编写一个Web应用 二、Http协议1.http协议是什么2.h…...

【qml入门系列教程】:qml QtObject用法介绍
作者:令狐掌门 技术交流QQ群:675120140 博客地址:https://mingshiqiang.blog.csdn.net/ 文章目录 QtObject 是 Qt/QML 中的一个基础类型,通常用作创建一个没有 UI 的(不渲染任何东西的)纯逻辑对象。可以使用它来组织代码、存储状态或者作为属性和方法的容器。 以下是如何…...
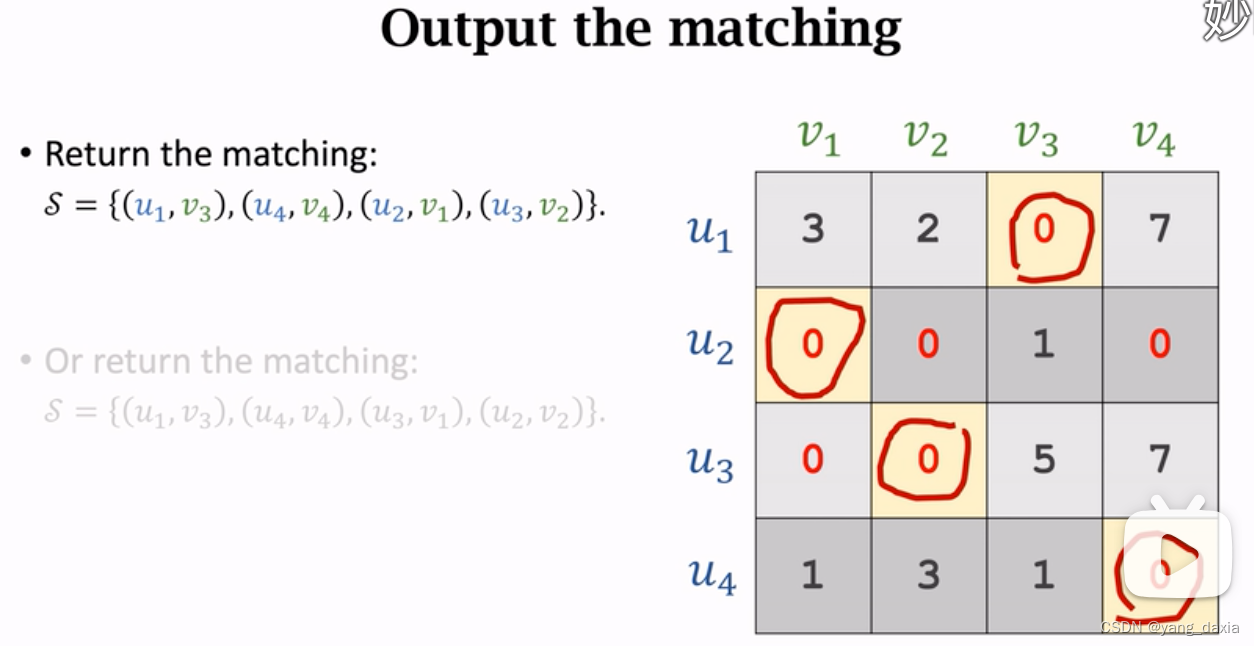
2分图匹配算法
定义 节点u直接无边,v之间无边,边只存在uv之间。判断方法:BFS染色法,全部染色后,相邻边不同色 无权二部图中的最大匹配 最大匹配即每一个都匹配上min(u, v)。贪心算法可能导致&…...
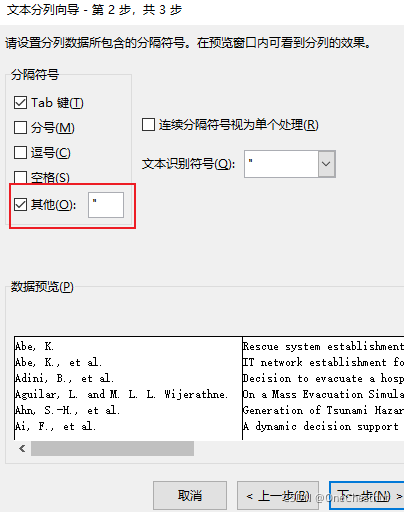
[EndNote学习笔记] 导出库中文献的作者、标题、年份到Excel
菜单栏Edit中,选择 Output Styles 在默认的 Annotated上进行修改,在Bibliography栏下的Templates中修改想要导出的格式 其中,每个粗体标题表示,针对不同的文献类型,设置相应的导出格式。一般为Journal Article&…...
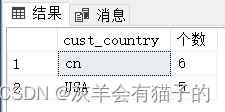
SQL Sever 基础知识 - 数据查询
SQL Sever 基础知识 - 一、查询数据 一、查询数据第1节 基本 SQL Server 语句SELECT第2节 SELECT语句示例2.1 SELECT - 检索表示例的某些列2.2 SELECT - 检索表的所有列2.3 SELECT - 对结果集进行筛选2.4 SELECT - 对结果集进行排序2.5 SELECT - 对结果集进行分组2.5 SELECT - …...

Vue入门——v-on标签
文章目录 规则v-on 一、案例总结 规则 v-on 作用:为html标签绑定事件语法: v-on:事件名:“函数名”简写为 事件名“函数名” 注意:函数需要定义在methods选项内部 一、案例 我们给案件绑定一个单击事件 <!DOCTYPE…...
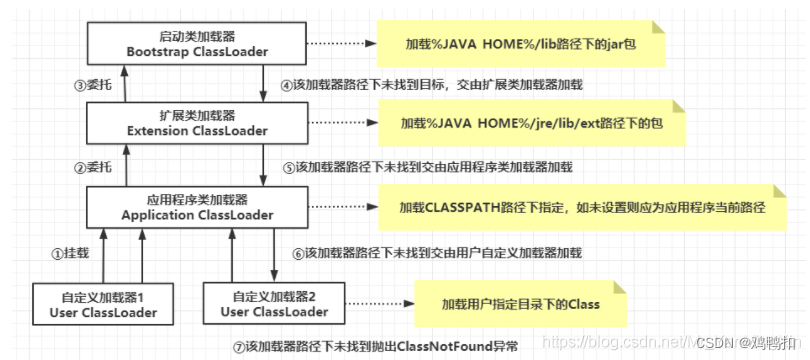
JVM:双亲委派(未完结)
类加载 定义 一个java文件从编写代码到最终运行,必须要经历编译和类加载的过程,如下图(图源自b站视频up主“跟着Mic学架构”)。 编译就是把.java文件变成.class文件。类加载就是把.class文件加载到JVM内存中,得到一…...

Leetcode 2661. 找出叠涂元素
Leetcode 2661. 找出叠涂元素题目 给你一个下标从 0 开始的整数数组 arr 和一个 m x n 的整数 矩阵 mat 。arr 和 mat 都包含范围 [1,m * n] 内的 所有 整数。从下标 0 开始遍历 arr 中的每个下标 i ,并将包含整数 arr[i] 的 mat 单元格涂色。请你找出 a…...

vscode代码调试配置
C/C代码调试 点击 vscode左侧的 run and debug,新建launch.json 和 tasks.json,并进行配置如下 launch.json {// Use IntelliSense to learn about possible attributes.// Hover to view descriptions of existing attributes.// For more informati…...

PTA 7-225 sdut-C语言实验- 冒泡排序中数据交换的次数
听说过冒泡排序么?一种很暴力的排序方法。今天我们不希望你用它来排序,而是希望你能算出从小到大冒泡排序的过程中一共进行了多少次数据交换。 输入格式: 输入数据的第一行为一个正整数 T ,表示有 T 组测试数据。 接下来T行,每行…...

新的 BLUFFS 攻击导致蓝牙连接不再私密
蓝牙是一种连接我们设备的低功耗无线技术,有一个新的漏洞需要解决。 中间的攻击者可以使用新的 BLUFFS 攻击轻松窥探您的通信。 法国研究中心 EURECOM 的研究员 Daniele Antonioli 演示了六种新颖的攻击,这些攻击被定义为 BLUFFS(蓝牙转发和…...
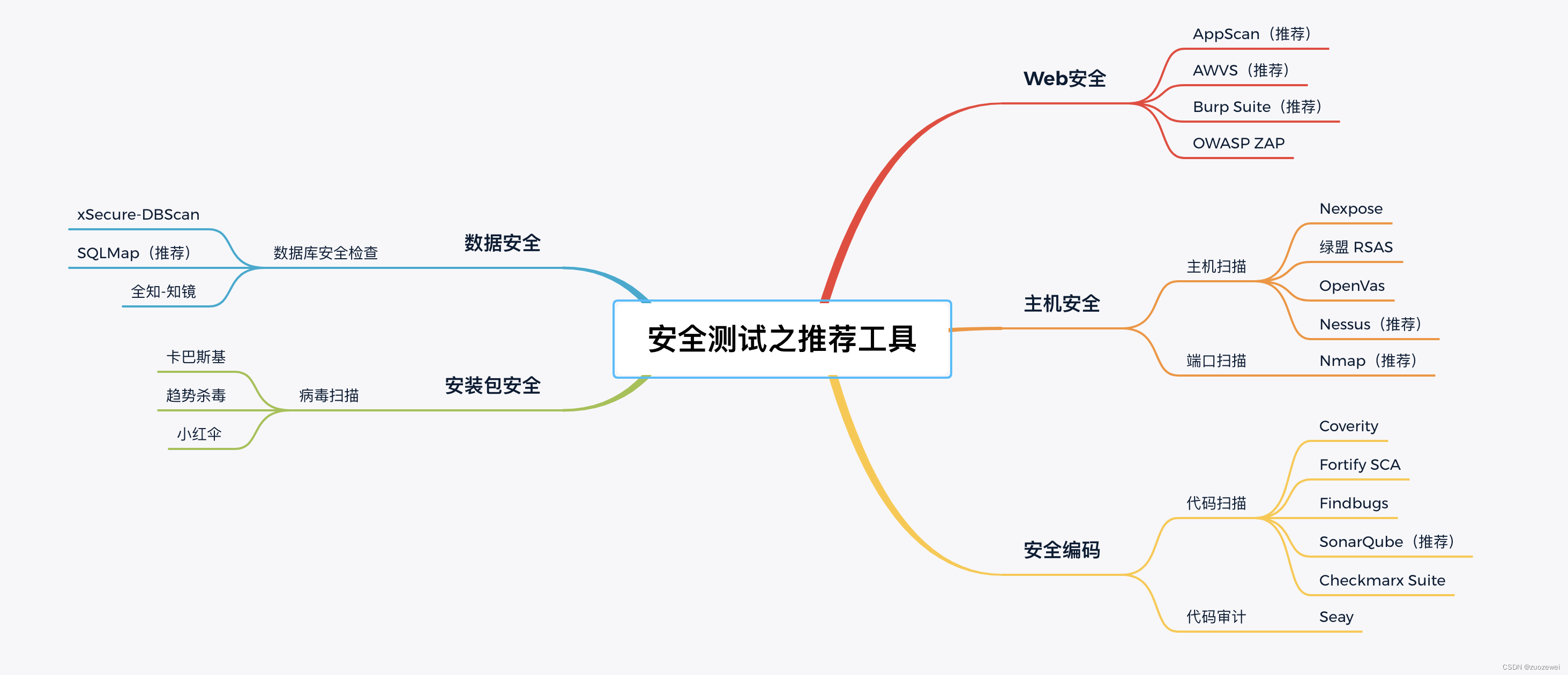
安全测试之推荐工具(一)
文章目录 一、前言二、Web安全(一)AppScan(推荐)(二)AWVS(推荐)(三)Burp Suite(推荐)(四)OWASP ZAP 三、主机安…...

final关键字
修饰 类,属性,方法,局部变量(包括方法参数) 类似c语言的const 使用方式: 1 不希望类被继承 用final类(类很重要,担心别人重写/修改) 2 不希望某…...

WPF MVVM模式下如何将UI窗口变量传参到Viewmodel层
WPF MVVM模式下如何将UI窗口变量传参到Viewmodel层 UI层窗口定义 //窗口中绑定ViewModel<hc:GlowWindow.DataContext><viewmodel:MainWindowViewModel /></hc:GlowWindow.DataContext>//注册初始化事件<hc:Interaction.Triggers><hc:EventTrigger…...

条款22:将成员变量声明为private
1.前言 首先,我们应该利用反证法,看看为什么成员变量不该是public,然后再了解所有反对public成员变量的论点同样适用于protected成员变量。最后得出一个结论:成员变量应该是private。 2.为什么不用public 如果成员变量不是publ…...

PTA 7-224 sdut-C语言实验-排序问题
输入10个整数,将它们从小到大排序后输出,并给出现在每个元素在原来序列中的位置。 输入格式: 输入数据有一行,包含10个整数,用空格分开。 输出格式: 输出数据有两行,第一行为排序后的序列,第二行为排序…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

