数据结构学习笔记——广义表
目录
- 一、广义表的定义
- 二、广义表的表头和表尾
- 三、广义表的深度和长度
- 四、广义表与二叉树
- (一)广义表表示二叉树
- (二)广义表表示二叉树的代码实现
一、广义表的定义
广义表是线性表的进一步推广,是由n(n≥0)个数据元素组成的有限序列。线性表中的数据元素只能是单个元素(原子),它是不可分割的,而广义表中的数据元素既可以是原子,也可以是一个广义表(包括空表和非空表),广义表通过圆括号“()”括起来,通过逗号“,”隔开表中的各个数据元素。

一个n维数组可以看成元素是n-1维数组的广义表,广义表的元素都是n-1维数组。广义表满足线性表的特征,只是其中的元素是原子或广义表(子表),分别只有一个表头元素和表尾元素,表头元素有后继但是没有前驱,表尾元素有前驱但是没有后继,剩下每个元素都有唯一的前驱和后继。
二、广义表的表头和表尾
广义表是可以递归的,一个广义表也可以是其自身的子表,广义表中的第一个元素称为广义表的表头,而剩余数据元素组成的表称为广义表的表尾,广义表的表头和表尾可以看作通过函数head()和tail()对广义表操作。例如,已知广义表S=(((a)),(b),c,(a),(((d,e)))),通过head()和tail()取出元素e的操作如下:
head(tail(head(head(head(tail(tail(tail(tail(A)))))))))
任何一个非空广义表,表头可能是单个元素(原子)或广义表,但表尾只可能是广义表,其原因是广义表的取表尾tail()是非空广义表除去表头元素后,剩余元素组成的表,所以不可能是原子。
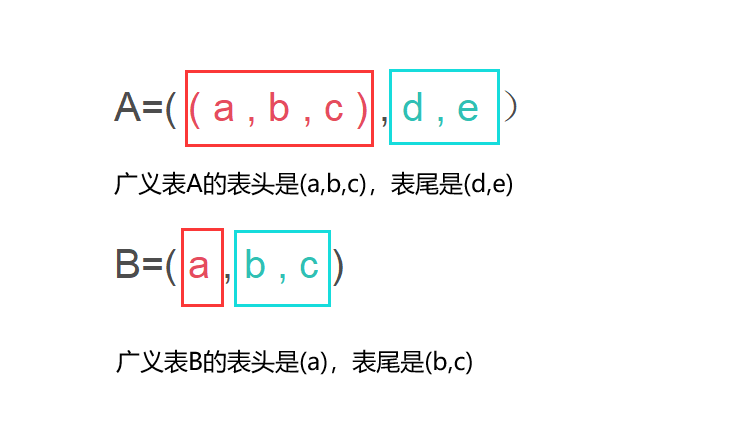
例如,C=(a,b,c,d,e,f,g),该广义表的表头是(a),表尾是(b,c,d,e,f,g);
例如,D=((a,b),((c,d,e),(f,g,h))),该广义表的表头是(a,b),表尾是((c,d,e),(f,g,h))。
另外,若一个广义表为空,则为一个空表。例如,E=( ),F=(( )),广义表E是一个空表,只有非空广义表才能取表头,广义表F的表头和表尾都是()。
三、广义表的深度和长度
- 广义表的深度通过
括号的层数求得,而长度是广义表中所含元素的个数。【深度层数,长度个数】
例如,一个空广义表G=(),括号层数为1,所以广义表的深度为1,而由于是空表,所以广义表的长度为0;
例如,一个广义表H=((a,b),(c,(d,e))),括号层数为3,所以广义表的深度为3,最高层为(c,(d,e)),逗号隔开了原子( c )和广义表( d,e ),元素个数为2,所以广义表的长度为2。
例如,一个广义表I=((),(a),(b,c,(d),((d,f)))),由于括号的最大层数为4,所以广义表的深度为4,可知广义表有三个元素,分别是()、(a)、(b,c,(d),((d,f))),元素个数为3,所以广义表的长度为3。
例如,设广义表J=(( ),( )),对广义表J,head(J)=( ),tail(J)=(( )),括号的最大层数为2,所以广义表的深度为2,广义表有两个元素,分别是()、(),元素个数为2,所以广义表长度为2。
注:这里的Tail(J)=(( )),而不是( )。
四、广义表与二叉树
(一)广义表表示二叉树
根据广义表中“ 数据元素既可以是原子,也可以是一个广义表(包括空表和非空表) ”这一点可以来表示二叉树,即通过(根结点,根结点的广义表)的形式来表示,其中可以嵌套。
例如,下面是一个满二叉树:
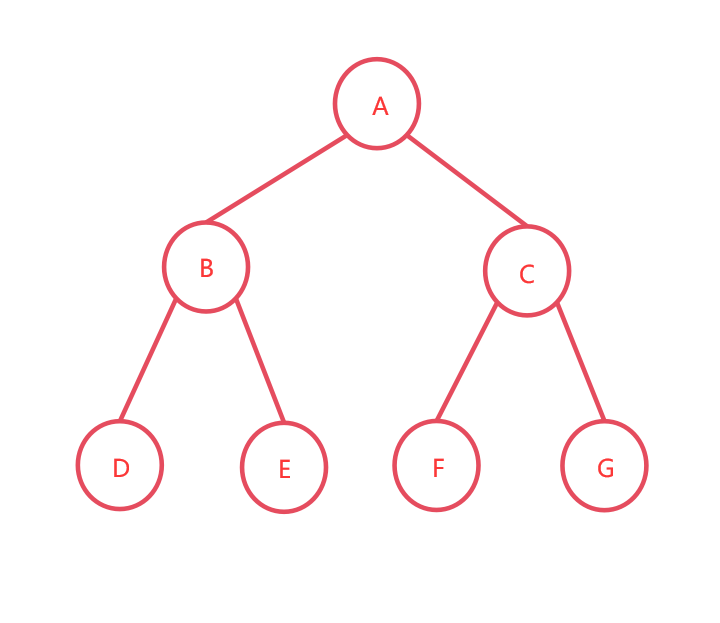
通过广义表表示该二叉树:
(A , ( B , ( D , E ) ) , ( C , ( F , G ) ) ) )
这个二叉树的解释如下:
根结点是A,它的左孩子是B,B的左孩子是D,B的右孩子是E。
根结点A的右孩子是C,C的左孩子是F,C的右孩子是G。
(二)广义表表示二叉树的代码实现
通过广义表来显示建立的二叉树,一个非空的二叉树T,当对于左孩子结点或右孩子结点时,此时输出一个左括号“(”,递归处理左子树,输出一个“,”用于隔开结点,然后递归处理右子树,输出一个右括号“)”,从而完成一个根结点以下的两个左/右结点处理,代码如下:
/*广义表输出二叉树*/
void ShowTree(BTree T) {if(T!=NULL) {//当二叉树不为空时printf("%c",T->data); //输入出该结点的数据域if(T->lchild!=NULL) { //若该结点的左子树不为空printf("("); //输出一个左括号ShowTree(T->lchild); //通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) { //若该结点右子树不为空printf(","); //输出一个逗号ShowTree(T->rchild); //通过递归继续输出结点的右子树结点下的各结点}printf(")"); //输出一个右括号} else { //若左子树为空,右子树不为空if(T->rchild!=NULL) {printf("("); //输出一个左括号ShowTree(T->lchild); //通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) { //若该结点的右子树不为空 printf(","); //输出一个逗号ShowTree(T->rchild); //通过递归继续输出结点的右子树结点下的各结点}printf(")"); //输出一个右括号}}}
}
例如,一个二叉树如下图,通过链式存储结构实现建立二叉树并输出。
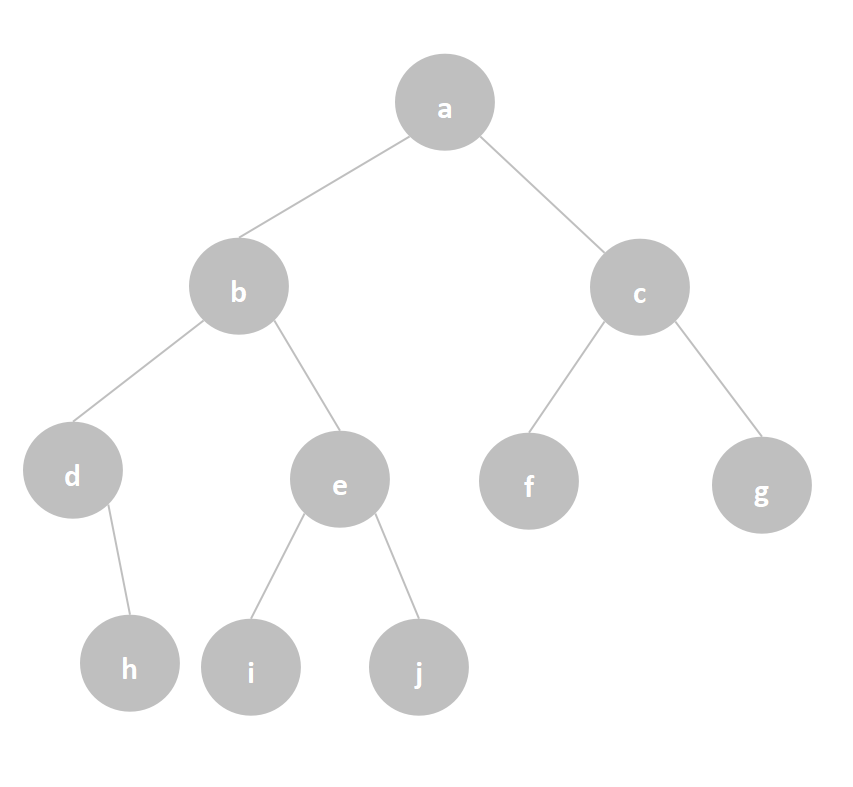
代码如下:
#include <stdio.h>
#include <malloc.h>
/*1、二叉树的定义*/
typedef struct BNode {int data; //数据域struct BNode *lchild,*rchild; //左孩子、右孩子指针
} *BTree;/*2、二叉树的建立*/
BTree CreateTree() {BTree T;char ch;scanf("%c",&ch);getchar(); //getchar()用于接收每次输入字符结点后的回车符,从而以便输入下一个字符结点if(ch=='0') //当为0时,将结点置空T=NULL;else {T=(BTree)malloc(sizeof(BTree)); //分配一个新的结点T->data=ch;printf("请输入%c结点的左孩子结点:",T->data);T->lchild=CreateTree(); //通过递归建立左孩子结点printf("请输入%c结点的右孩子结点:",T->data);T->rchild=CreateTree(); //通过递归建立右孩子结点}return T;
}/*3、广义表输出二叉树*/
void ShowTree(BTree T) {if(T!=NULL) {//当二叉树不为空时printf("%c",T->data); //输入出该结点的数据域if(T->lchild!=NULL) { //若该结点的左子树不为空printf("("); //输出一个左括号ShowTree(T->lchild); //通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) { //若该结点右子树不为空printf(","); //输出一个逗号ShowTree(T->rchild); //通过递归继续输出结点的右子树结点下的各结点}printf(")"); //输出一个右括号} else { //若左子树为空,右子树不为空if(T->rchild!=NULL) {printf("("); //输出一个左括号ShowTree(T->lchild); //通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) { //若该结点的右子树不为空 printf(","); //输出一个逗号ShowTree(T->rchild); //通过递归继续输出结点的右子树结点下的各结点}printf(")"); //输出一个右括号}}}
}/*主函数*/
int main() {BTree T;T=NULL;printf("请输入二叉树的根结点:");T=CreateTree(); //建立二叉树printf("建立的二叉树如下:\n");ShowTree(T); //通过广义表显示二叉树
}
依次输入各个结点的左右孩子结点,若结点不存在则输入0,例如树中结点d的左孩子结点不存在,结点f、g、h、i、j的左右孩子都不存在,输入时都输入0。
运行结果如下,结果通过广义表的定义显示:
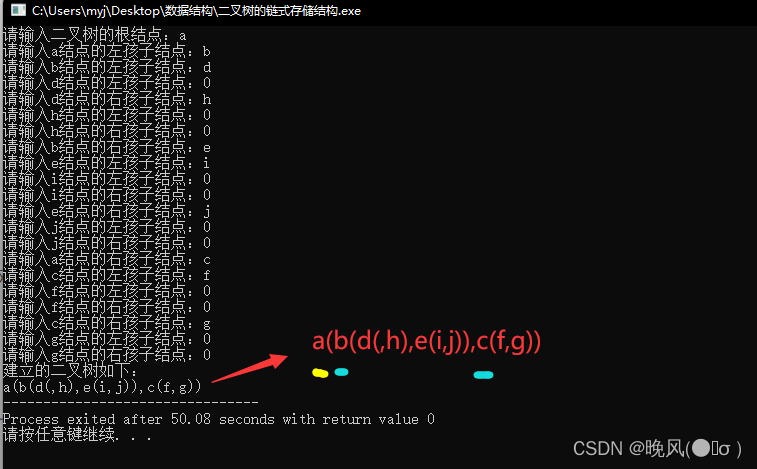
相关文章:

数据结构学习笔记——广义表
目录 一、广义表的定义二、广义表的表头和表尾三、广义表的深度和长度四、广义表与二叉树(一)广义表表示二叉树(二)广义表表示二叉树的代码实现 一、广义表的定义 广义表是线性表的进一步推广,是由n(n≥0&…...
)
为什么每次optimizer.zero_grad()
当你训练一个神经网络时,每一次的传播和参数更新过程可以被分解为以下步骤: 1前向传播:网络对输入数据进行操作,最终生成输出。这个过程会基于当前的参数(权重和偏差)计算出一个或多个损失函数的值。 2计…...

一个页面从输入 URL 到页面加载显示完成,这个过程中都发生了什么
一个页面从输入URL到加载显示完成经历了以下过程: DNS解析:浏览器会解析URL中的域名,将其转换为对应的IP地址。如果浏览器缓存中存在该域名的IP地址,则跳过DNS解析步骤。 建立TCP连接:通过解析得到的IP地址࿰…...

iOS ------ UICollectionView
一,UICollectionView的简介 UICollectionView是iOS6之后引入的一个新的UI控件,它和UITableView有着诸多的相似之处,其中许多代理方法都十分类似。简单来说,UICollectionView是比UITbleView更加强大的一个UI控件,有如下…...
ElasticSearch知识体系详解
1.介绍 ElasticSearch是基于Lucene的开源搜索及分析引擎,使用Java语言开发的搜索引擎库类,并作为Apache许可条款下的开放源码发布,是当前流行的企业级搜索引擎。 它可以被下面这样准确的形容: 一个分布式的实时文档存储…...

Linux自启服务提示:systemd[1]: *.service: main process exited, code=exited, status=1问题
这两天一直在沉迷于配脚本,由于服务器很多,所以我都是从一台服务器上配置好的脚本直接copy到另一台服务器,按说完全一样的脚本一样的操作,那么应该是一样的执行结果 but, Gul’dan,代…我重启服务器后服务并没有正常启…...
LoadBalancer将服务暴露到外部实现负载均衡purelb-layer2模式配置介绍
目录 一.purelb简介 1.简介 2.purelb的layer2工作模式特点 二.layer2的配置演示 1.首先准备ipvs和arp配置环境 2.purelb部署开始 (1)下载purelb-complete.yaml文件并应用 (2)查看该有的资源是否创建完成并运行 ÿ…...
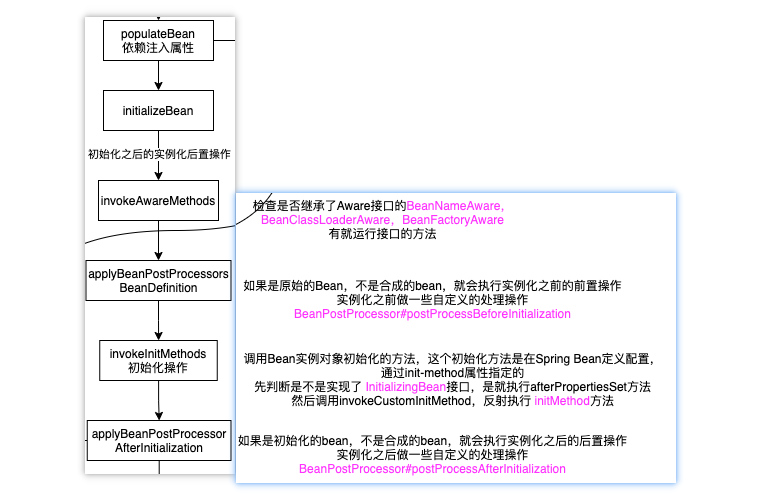
Spring Bean的生命周期各阶段详解附源码
目录 Bean的生命周期Bean定义阶段Bean实例化阶段Bean属性注入阶段Bean初始化阶段Bean销毁阶段 Bean的生命周期 bean的生命周期,我们都知道大致是分为:bean定义,bean的实例化,bean的属性注入,bean的初始化以及bean的销毁…...
LoadBalancer将服务暴露到外部实现负载均衡Openelb-layer2模式配置介绍
目录 一.openelb简介 二.主要介绍layer2模式 1.简介 2.原理 3.部署 (1)先在集群master上开启kube-proxy的strictARP (2)应用下载openelb.yaml(需要修改镜像地址) (3)编写yam…...

Android异步之旅:探索IntentService
1.介绍IntentService IntentService是Android中的一个Service类,用于在后台执行耗时操作,而不会阻塞UI线程。它封装了HandlerThread和Handler,使得我们可以方便地在后台执行任务,而不需要自己管理线程和消息处理。 以下是 Intent…...
)
131.类型题-计算数学序列的和,请编写函数fun,其功能是S=……【满分解题代码+详细分析】(数学序列的和类型题-C/C++JavaPython实现)
文章目录 131.类型题-计算数学序列的和:计算并输出一.题目1.1 解题思路二.解题代码2.1 C/C++解题代码2.2 python解题代码2.3 Java解题代码三.解题代码仔细分析3.1 C/C++解题代码仔细分析3.2 Java解题代码仔细分析3.3 Python解题代码仔细分析四.本类型题解题诀窍五.寄语131.类型…...
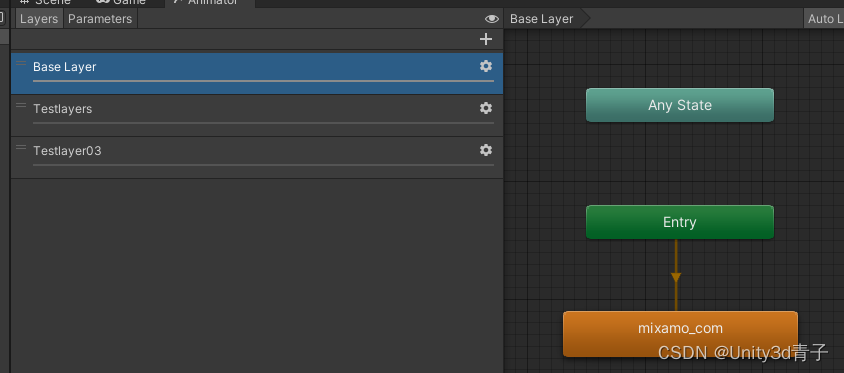
【Unity动画】状态机中层的融合原理与用法详解
1. 状态机概念介绍 在Unity中,动画状态机(Animator State Machine)是一种强大的工具,用于控制游戏对象的动画行为。动画状态机由多个动画状态Animation和过渡条件Transition、层组成!而层(Layersÿ…...

等保之道:从基础出发,解密网站防护的重要性
随着数字化时代的推进,网站安全问题日益凸显。网站被攻击不仅会导致信息泄漏、服务中断,还可能损害用户信任和企业声誉。为了更好地解决这一问题,我们需从等保的角度审视网站防护,全面提升网络安全水平。 等保背景 等保࿰…...

7. 系统信息与系统资源
7. 系统信息与系统资源 1. 系统信息1.1 系统标识 uname()1.2 sysinfo()1.3 gethostname()1.4 sysconf() 2. 时间、日期2.1 Linux 系统中的时间2.1.1 Linux 怎么记录时间2.1.2 jiffies 的引入 2.2 获取时间 time/gettimeofday2.2.1 time()2.2.2 gettimeofday() 2.3 时间转换函数…...

【重点】【滑动窗口】239. 滑动窗口最大值
题目 也可参考:剑指offer——面试题65:滑动窗口的最大值 class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int[] res new int[nums.length - k 1];Deque<Integer> q new LinkedList<>();int inx 0;while (inx <…...

d3dx9_43.dll丢失原因以及5个解决方法详解
在电脑使用过程中,我们可能会遇到一些错误提示,其中之一就是“d3dx9_43.dll缺失”。这个错误提示通常表示我们的电脑上缺少了DirectX的一个组件,而DirectX是游戏和多媒体应用所必需的软件。本文将介绍d3dx9_43.dll缺失对电脑的影响以及其原因…...
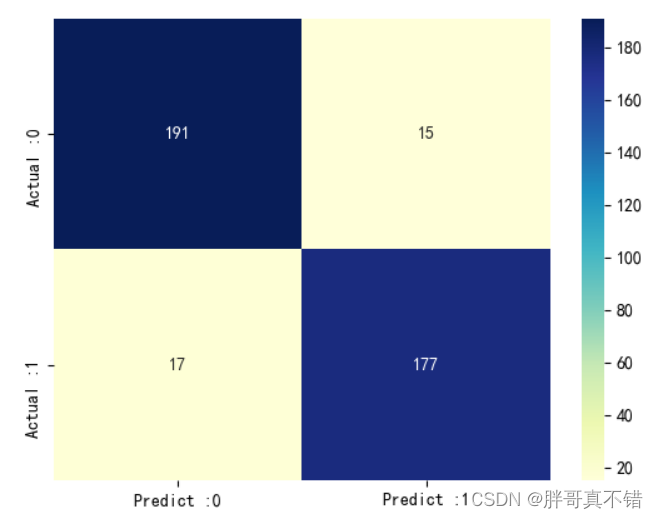
Python实现FA萤火虫优化算法优化卷积神经网络分类模型(CNN分类算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 萤火虫算法(Fire-fly algorithm,FA)由剑桥大学Yang于2009年提出 , …...

不瞒各位,不安装软件也能操作Xmind文档
大家好,我是小悟 作为搞技术的一个人群,时不时就要接收产品经理发过来的思维脑图,而此类文档往往是以Xmind编写的,如果你的电脑里面没有安装Xmind的话,不好意思,是打不开这类后缀结尾的文档。 打不开的话…...

你了解Redis 的二进制安全吗
最近面试的时候被问到Redis 的二进制安全相关八股文面试题。Redis二进制安全内容比较多,以下是简单的总结大致的过程,需要深入学习的建议跳过 Redis是基于C语言进行开发的,而C语言中的字符串是二进制不安全的,所以Redis就没有直接…...
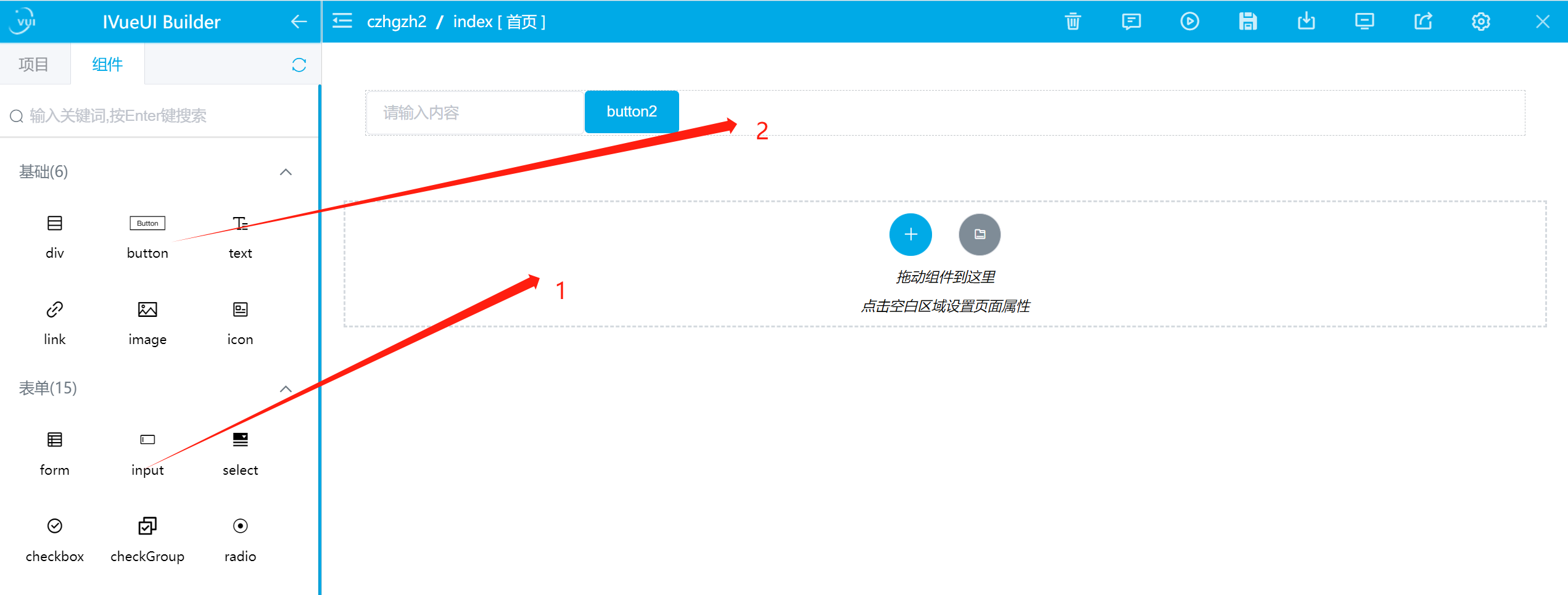
探索前端设计的新境界——介绍IVueUI工具助力Vue页面设计
在快速发展的前端领域,Vue.js作为一款渐进式JavaScript框架,一直备受开发者喜爱。然而,在Vue前端开发的旅程中,页面设计常常是一个不可避免的挑战。今天,我要向大家介绍一款令Vue前端开发者受益匪浅的工具——www.ivue…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
