PTA 7-236 验证哥德巴赫猜想
哥德巴赫猜想之一是指一个偶数(2除外)可以拆分为两个素数之和。请验证这个猜想。
因为同一个偶数可能可以拆分为不同的素数对之和,这里要求结果素数对彼此最接近。
输入格式:
首先输入一个正整数T,表示测试数据的组数,然后是T组测试数据。每组测试输入1个偶数n(6≤n≤10000)。
输出格式:
对于每组测试,输出两个彼此最接近的素数a、b(a≤b),两个素数之间留1个空格。
输入样例:
2
30
40
输出样例:
13 17
17 23思路:
-
定义一个全局数组
prime,用于存储从6到10000之间所有的素数,空间要足够大,否则会段错误 -
调用
is_prime函数检查6到10000之间的每个整数是否为素数,并将素数存入prime数组 -
查找能够相加得到该偶数的一对素数,并且这对素数的差距尽可能小
/*
一个偶数(2除外)可以拆分为两个素数之和
两个素数a、b彼此最接近
*/#include <stdio.h>
#include <math.h>int prime[5000];// 统计6~10000间的所有素数(数组给太小会段错误)
int is_prime(int x)
{int flag=1;if(x==1)flag=0;for(int i=2;i<=sqrt(x);i++){if(x%i==0){flag=0;break;}}return flag;
}void two_prime(int sum,int cnt)
{int a,b;for(int i=0;i<cnt;i++)// a<=b{for(int j=i;j<cnt;j++){if((prime[i]+prime[j] == sum)){a=prime[i];b=prime[j];}}}printf("%d %d\n",a,b);// for(int i=0;i<10;i++)// printf("%d ",prime[i]);// printf("\n");
}
int main()
{int T,num;int cnt=0;for(int nums=6;nums<=10000;nums++){if(is_prime(nums))prime[cnt++]=nums;}scanf("%d",&T);while(T--){scanf("%d",&num);two_prime(num,cnt);}return 0;
}
相关文章:

PTA 7-236 验证哥德巴赫猜想
哥德巴赫猜想之一是指一个偶数(2除外)可以拆分为两个素数之和。请验证这个猜想。 因为同一个偶数可能可以拆分为不同的素数对之和,这里要求结果素数对彼此最接近。 输入格式: 首先输入一个正整数T,表示测试数据的组数࿰…...

微信小程序 纯css画仪表盘
刚看到设计稿的时候第一时间想到的就是用canvas来做这个仪表盘,虽然本人的画布用的不是很好但还可以写一写😀。话不多说直接上代码。最后有纯css方法 <!--wxml--> <canvas canvas-id"circle" class"circle" >// js dat…...
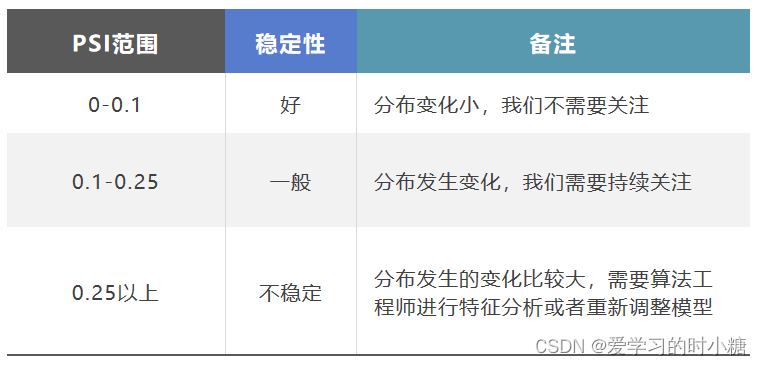
成为AI产品经理——模型稳定性评估(PSI)
一、PSI作用 稳定性是指模型性能的稳定程度。 上线前需要进行模型的稳定性评估,是否达到上线标准。 上线后需要进行模型的稳定性的观测,判断模型是否需要迭代。 稳定度指标(population stability index ,PSI)。通过PSI指标,我们可以获得不…...
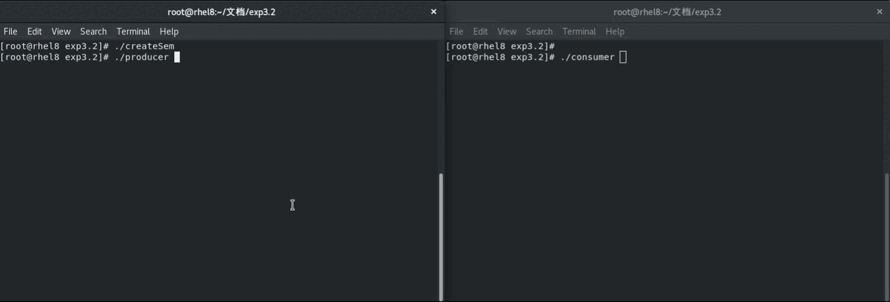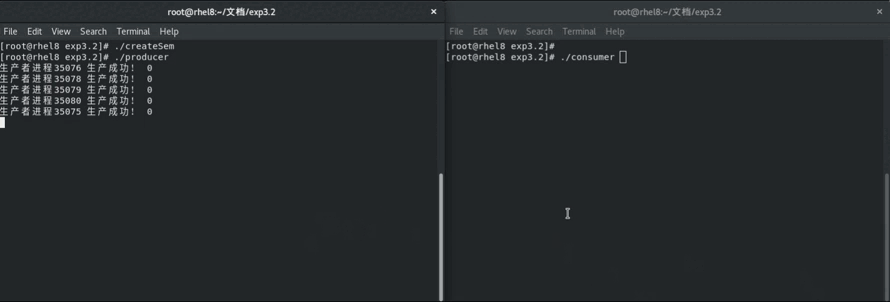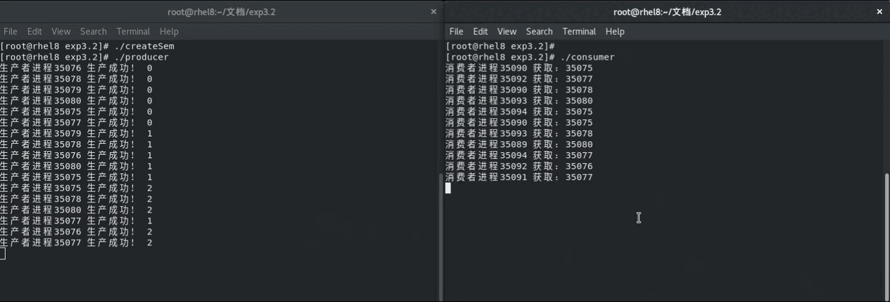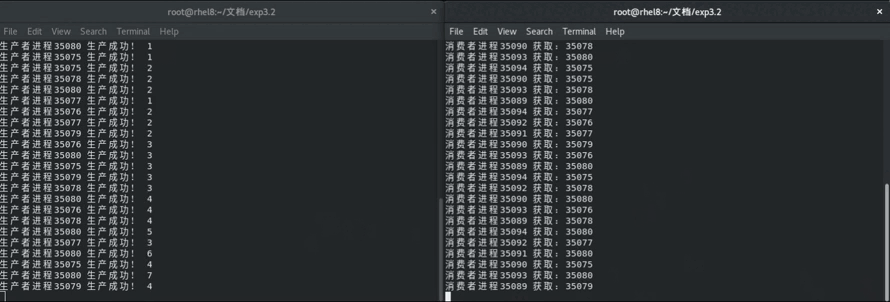
操作系统——进程同步
目录 一、信号量相关函数 1. 创建信号量集 2. 获取信号量集 3. 等待、通知信号量集 4. 控制信号量集 二、简单进程同步 1. 创建信号量集 2. P操作 3. V操作 4. 删除信号量集 5. 测试: 三、生产者与消费者 1. 创建、删除共享内存及信号量集 2. 单一生产…...
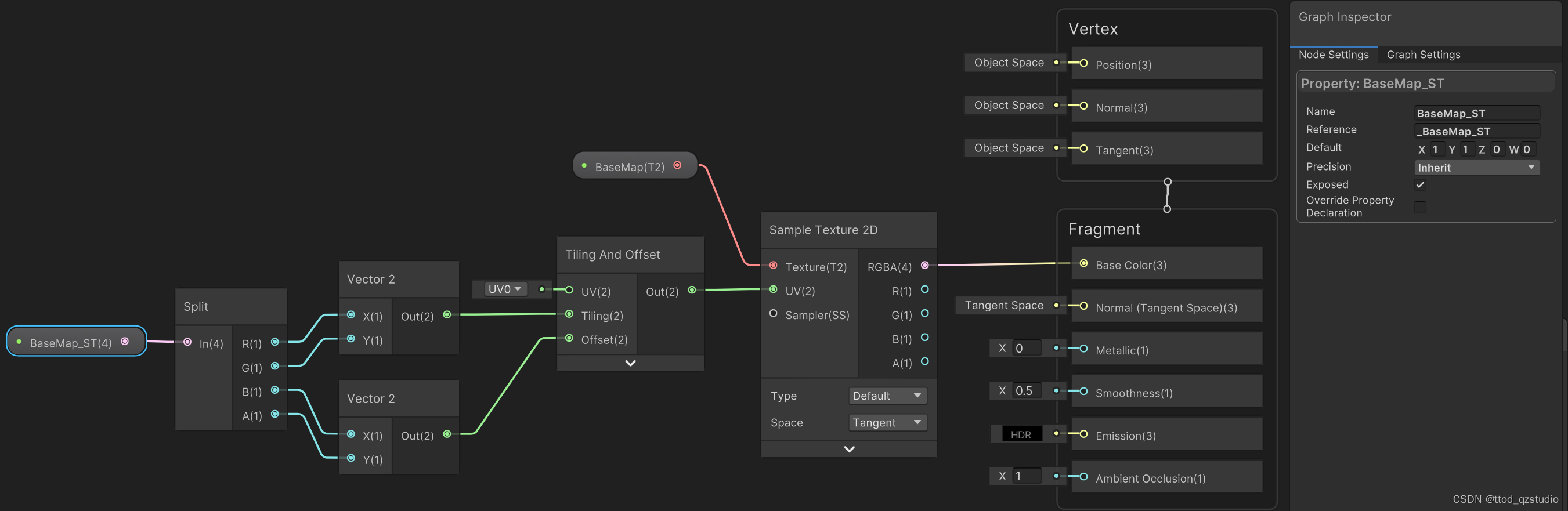
如何能够对使用ShaderGraph开发的Shader使用SetTextureOffset和SetTextureScale方法
假设在ShaderGraph中的纹理的引用名称为"_BaseMap",同时对这个"_BaseMap"纹理使用了采样的节点"SampleTexture2D",然后该采样节点的uv接入的TilingAndOffset节点,此时的关键步骤是新建一个Vector4属性…...
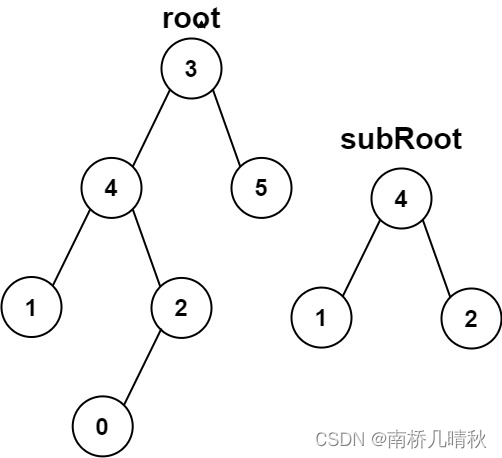
力扣572:另一棵树的子树
力扣572:另一棵树的子树 给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。 二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所…...

Linux系统中进程间通信(Inter-Process Communication, IPC)
文章目录 进程间通信介绍进程间通信目的进程间通信发展 管道什么是管道 匿名管道用fork来共享管道原理站在文件描述符角度-深度理解管道站在内核角度-管道本质管道读写规则管道特点 命名管道创建一个命名管道匿名管道与命名管道的区别命名管道的打开规则 命名管道的删除用命名管…...
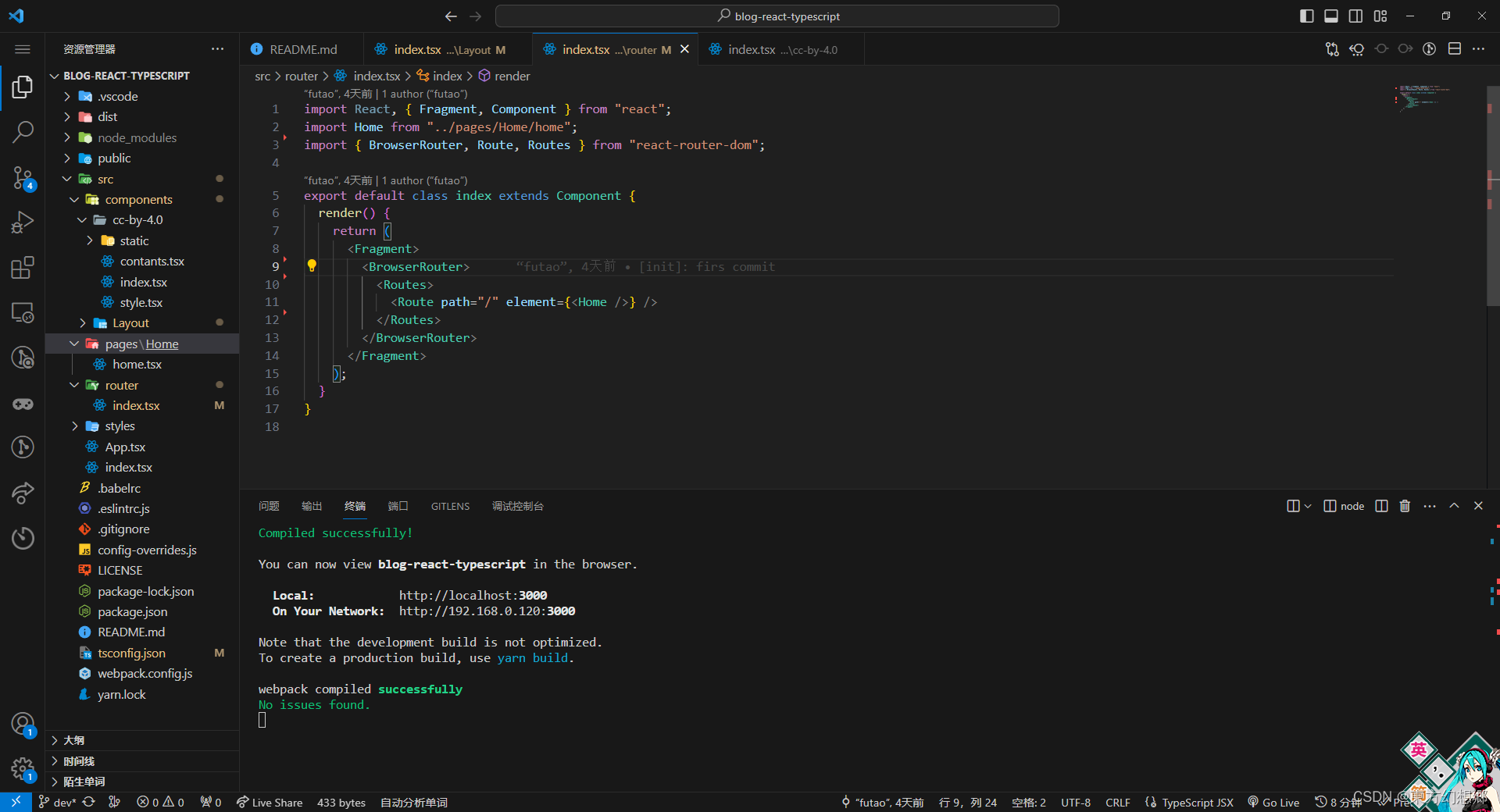
【React + Typescript】使用WebPack包管理、各种扩展插件组成的初始模板,开源协议:CC-BY-4.0
React Typescript Webpack 模板 模板展示项目结构使用的部分扩展包页面配置代码Layout 公共容器组件路由Jspackage.json 开源模板下载TIP 模板展示 项目结构 使用的部分扩展包 📂 System ├── 📂 Plugin │ ├── 📄 file-loader | 在处…...

python 制作3d立体隐藏图
生成文件的3d图,例子: 文字: 隐藏图: 使用建议: 1、建议不用中文,因为中文太复杂,生成立体图效果不好。 2、需要指定FONT_PATH,为一个ttf文件,…...
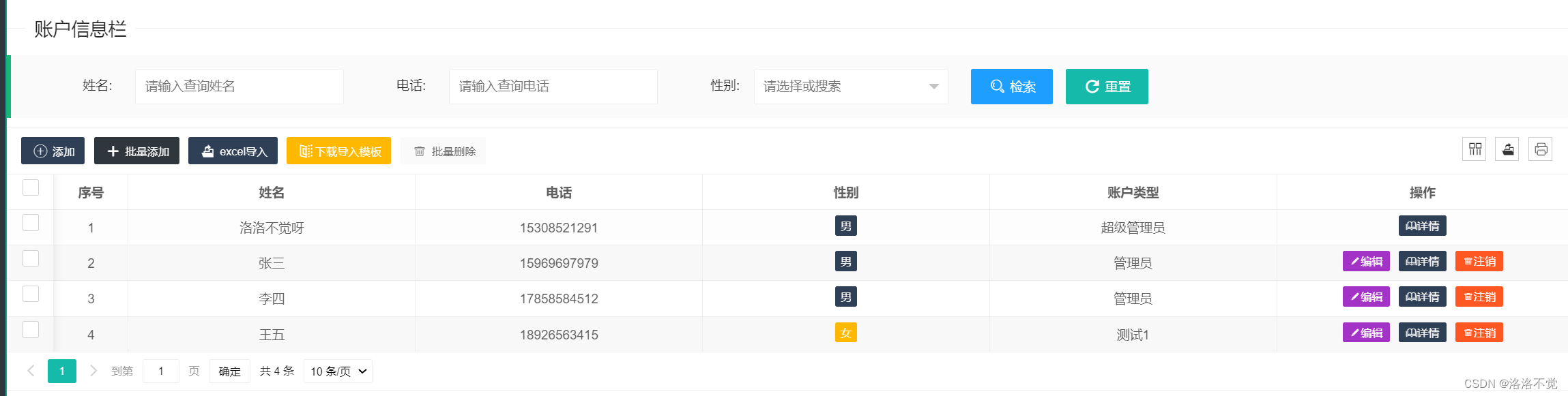
layui+ssm实现数据批量删除
layuissm实现数据的批量删除 //数据表格table.render({id: adminList,elem: #adminList,url: ctx "/admin/getAdminList", //数据接口cellMinWidth: 80,even: true,toolbar: #toolbarDemo,//头部工具栏limit: 10,//每页条数limits: [10, 20, 30, 40],defaultToolba…...

国产AI边缘计算盒子,双核心A55丨2.5Tops算力
边缘计算盒子 双核心A55丨2.5Tops算力 ● 2.5TopsINT8算力,支持INT8/INT4/FP16多精度混合量化。 ● 4路以上1080p30fps视频编解码,IVE模块独立提供图像基础算子加速。 ● 支持Caffe、ONNX/PyTorch深度学习框架,提供resnet50、yolov5等AI算…...

C++作业4
代码整理, 将学过的三种运算符重载,每个至少实现一个运算符的重载 代码: #include <iostream>using namespace std;class Stu {friend const Stu operator*(const Stu &L,const Stu &R);friend bool operator<(const Stu …...
| 物理层上 | 数据通信基础知识 调制 频率范围 信噪比)
计算机网络(二)| 物理层上 | 数据通信基础知识 调制 频率范围 信噪比
文章目录 1 物理层基本概念2.数据通信基础知识2.1 数据通信基本概念2.2 信道基本概念2.2.1 基带调制(编码)方式2.2.2 带通调制方式 2.3 信道的极限速率影响因素2.3.1 **频率范围**2.3.2 **信噪比** 内容笔记来源于谢希任老师《计算机网络》 物理层重点 …...
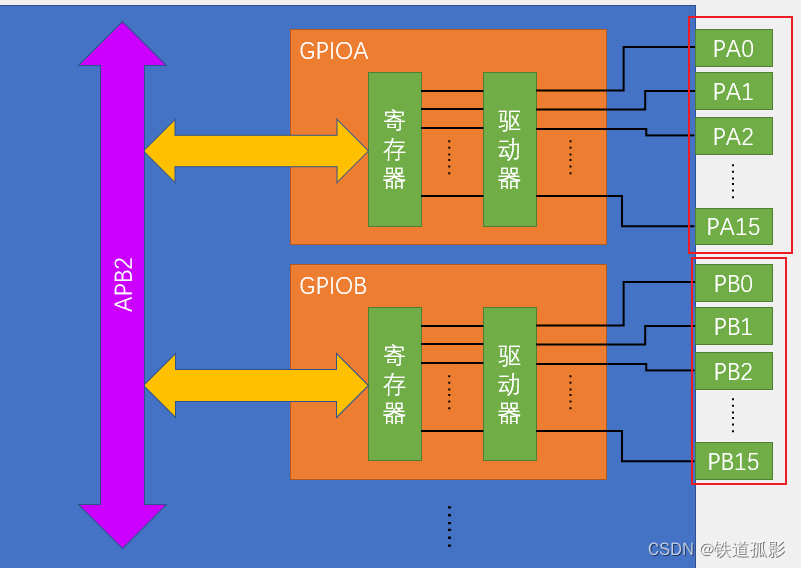
[STM32-1.点灯大师上线】
学习了江协科技的前4课,除了打开套件的第一秒是开心的,后面的时间都是在骂娘。因为51的基础已经几乎忘干净,c语言已经还给谭浩强,模电数电还有点底子,硬着头皮上吧。 本篇主要是讲述学习点灯的过程和疑惑解释。 1.工…...

Web测试自动化工具Selenium的使用
Web测试自动化工具Selenium的使用 Selenium是一个Web应用测试的自动化工具,它通过模拟点击实现对Web应用的功能测试。测试时,除了Selenium,还需要对应的浏览器驱动,如在Chrome实现自动点击,则需要chromedriver。 Sel…...

VUE2+THREE.JS 按照行动轨迹移动人物模型并相机视角跟随人物
按照行动轨迹移动人物模型并相机视角跟随人物 1. 初始化加载模型2. 开始移动模型3. 人物模型启动4. 暂停模型移动5. 重置模型位置6. 切换区域动画7. 摄像机追踪模型8. 移动模型位置9.动画执行 人物按照上一篇博客所设定的关键点位置,匀速移动 1. 初始化加载模型 //…...

Hadoop YARN组件
1. 请解释Yarn的基本架构和工作原理。 YARN,也被称为"Yet Another Resource Negotiator",是Apache HadoopYARN,也被称为"Yet Another Resource Negotiator",是Apache Hadoop的一部分,它被设计为一…...

Java架构师技术架构路线
目录 1 概论2 如何规划短中长期的技术架构路线图3 如何规划面向未来的架构4 如何修订路线图执行过程中的偏差5 如何落地路线图-阿里系糙快猛之下的敏捷模式想学习架构师构建流程请跳转:Java架构师系统架构设计 1 概论 首先,规划一个短中长期的技术路线图是非常重要的。短中…...

guacamole docker一键部署脚本
前言 在我学习guacamole的过程中发现全网大致有两种方式安装guacamole的方式: 1. 直接安装(下载java环境/mysql/, 修改配置) 2. docker安装(和直接安装类似,需要下载相关环境,然后做配置) 然…...

蓝桥杯算法心得——想吃冰淇淋和蛋糕(dp)
大家好,我是晴天学长,dp题,怎么设计状态很重要,需要的小伙伴可以关注支持一下哦!后续会继续更新的。💪💪💪 1) .想吃冰淇淋和蛋糕 想吃冰淇淋与蛋糕 输入格式 第一行输入一个整数n。…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...
