【C语言】递归详解
目录
- 1.前言
- 2. 递归的定义
- 3. 递归的限制条件
- 4. 递归举例
- 4.1 求n的阶乘
- 4.1.1 分析和代码实现
- 4.1.2 画图演示
- 4.2 顺序打印一个整数的每一位
- 4.2.1 分析和代码实现
- 4.2.2 画图推演
- 4.3 求第n个斐波那契数
- 5. 递归与迭代
- 5.1 迭代求第n个斐波那契数
1.前言
这次博客内容是与递归有关,递归是学习C语⾔函数绕不开的⼀个话题,那什么是递归呢?接下来正⽂开始。
2. 递归的定义
递归其实是一种解决问题的方法,在C语言中,递归就是函数自己调用自己。
来看看一个简单的C语言递归代码
#include <stdio.h>
int main()
{printf("hehe\n");main();//main函数中⼜调⽤了main函数return 0;
}
上述就是⼀个简单的递归程序,只不过上⾯的递归只是为了演示递归的基本形式,不是为了解决问题,代码最终也会陷⼊死递归,导致栈溢出。

递归的思想:
把⼀个大型复杂问题层层转化为⼀个与原问题相似,但规模较小的子问题来求解;直到子问题不能再被拆分,递归就结束了。所以递归的思考方式就是把大事化小的过程。
递归中的递就是递推的意思,归就是回归的意思,接下来慢慢来体会。
3. 递归的限制条件
递归在书写的时候,有2个必要条件:
- 递归存在限制条件,当满足这个限制条件的时候,递归便不再继续。
- 每次递归调用之后越来越接近这个限制条件
在下面的例子中,我们体会一下这2个限制条件。
4. 递归举例
4.1 求n的阶乘
计算n的阶乘(不考虑溢出),n的阶乘就是1~n的数字累积相乘。
4.1.1 分析和代码实现

将5的阶乘分成4的阶乘乘5;
将4的阶乘分成3的阶乘乘4;
将3的阶乘分成2的阶乘乘3;
将2的阶乘分成1的阶乘乘2;

这样的思路就是把⼀个较大的问题,转换为⼀个与原问题相似,但规模较小的问题来求解的。直到n是1或者0时,不再拆解
最终将n的阶乘就写成n*(n-1)!
直到n是1或者0时,不再拆解
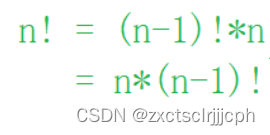
如果将阶乘写成一个函数Fact(n),
那么Fact(n)=n*Fact(n-1)
再稍微分析一下,当 n<=1 的时候,n的阶乘是1,其余n的阶乘都是可以通过上述公式计算。
n的阶乘的递归公式如下:
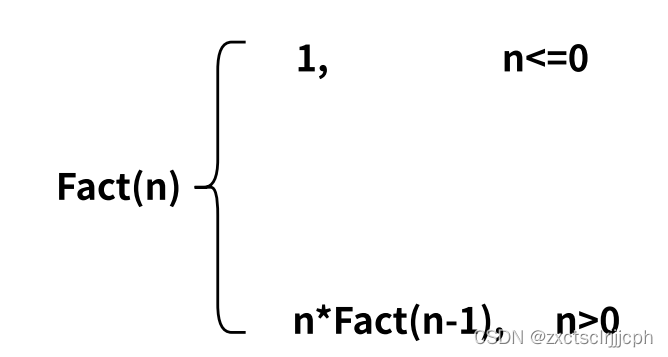
那我们就可以写出函数Fact求n的阶乘,假设Fact(n)就是求n的阶乘,那么Fact(n-1)就是求n-1的阶乘,函数如下:
int Fact(int n)
{if(n<=0)return 1;elsereturn n*Fact(n-1);
}
来测试一下:
int Fact(int n)
{if(n<=0)return 1;elsereturn n*Fact(n-1);
}int main()
{int n = 0;scanf("%d", &n);int ret = Fact(n);printf("%d\n", ret);return 0;
}
我们知道3的阶乘就是321=6,结果显然是我们所想的。
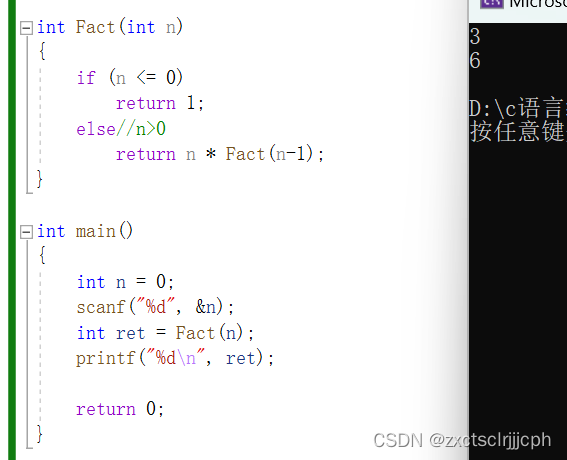
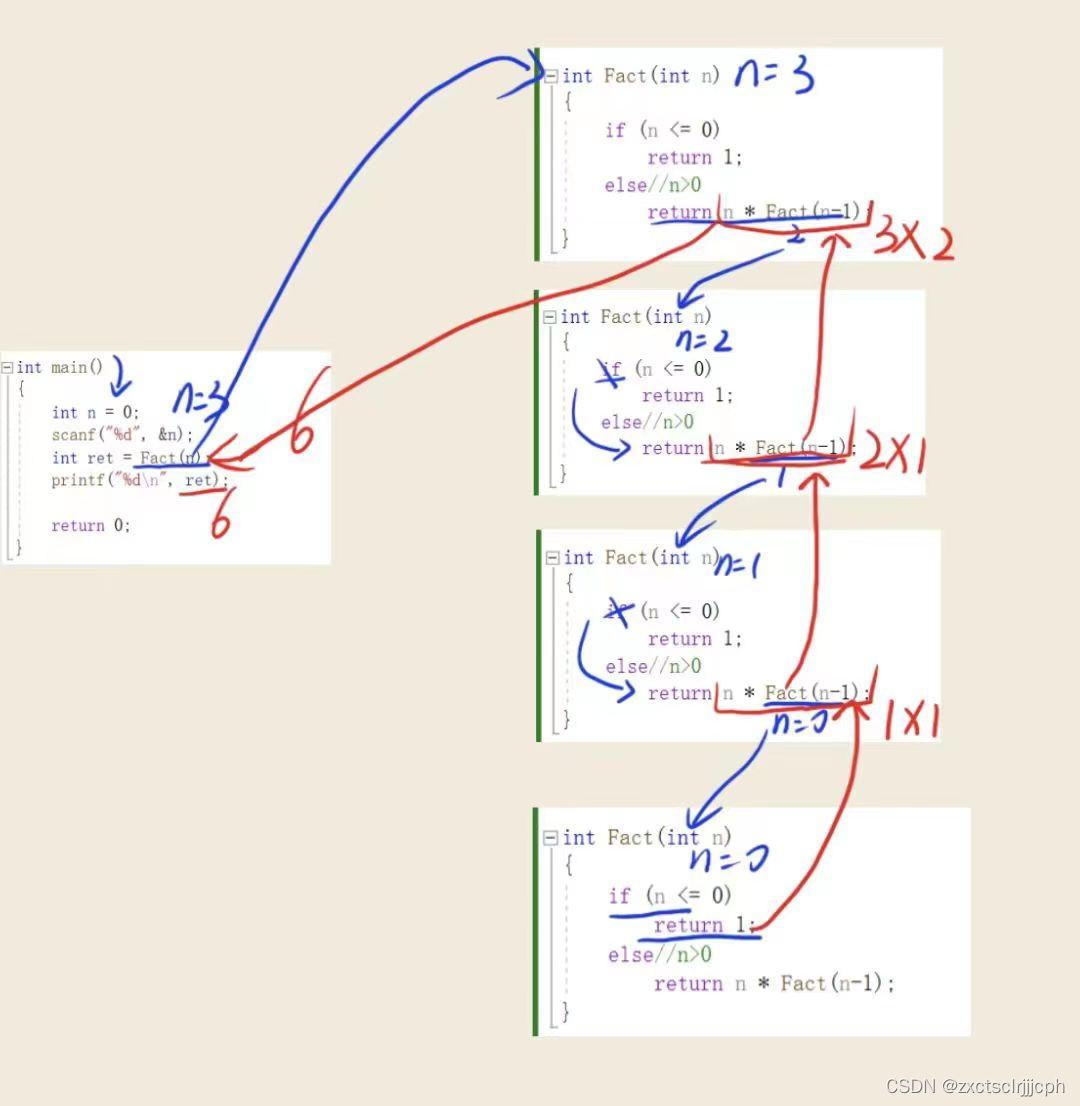
4.1.2 画图演示
蓝色是递推的过程,此时并没有开始相乘。
而红色是回归的过程,此时回归时相乘。
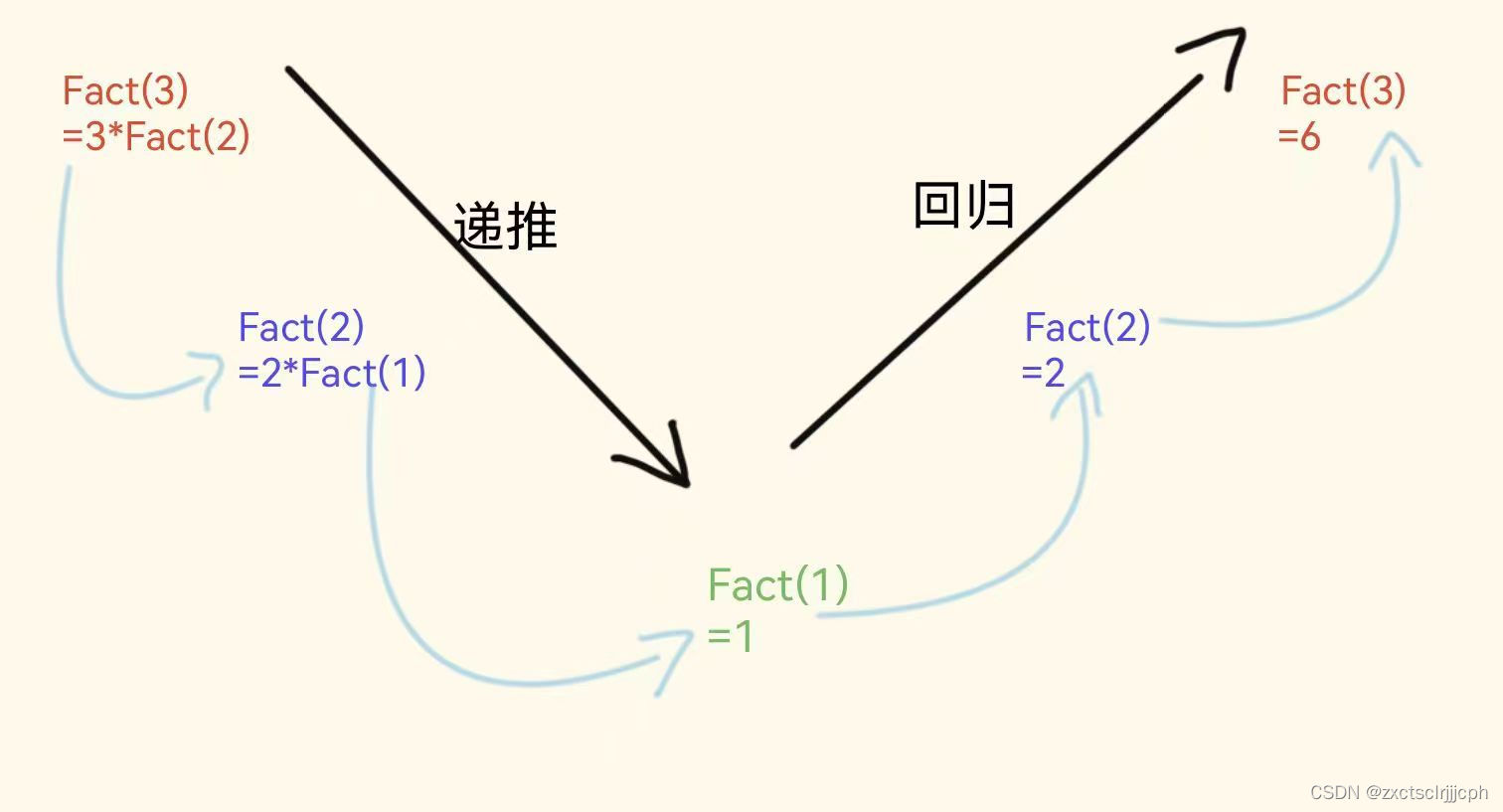
4.2 顺序打印一个整数的每一位
输⼊一个整数n,打印这个按照顺序打印整数的每⼀位
输⼊:1234 输出:1 2 3 4
输⼊:521 输出:5 2 1
4.2.1 分析和代码实现
这个题目,放在我们面前,首先想到的是,怎么得到这个数的每一位呢?
1234%10就能得到4,然后1234/10得到123,这就相当于去掉了4;
然后继续对123%10,就得到了3,再除10去掉3,以此类推;
不断的 %10 和 \10 操作,直到1234的每⼀位都得到;
但是这里有个问题就是得到的数字顺序是倒着的。
但是我们有了灵感,我们发现其实⼀个数字的最低位是最容易得到的,通过%10就能得到

那我们假设想写⼀个函数Print来打印n的每⼀位,如下表示:
Print(n)
如果n是1234,那表⽰为
Print(1234) //打印1234的每⼀位
其中1234中的4可以通过%10得到,那么
Print(1234)就可以拆分为两步:
- Print(1234/10) //打印123的每⼀位
- printf(1234%10) //打印4 完成上述2步,那就完成了1234每⼀位的打印 那么Print(123)⼜可以拆分为Print(123/10) + printf(123%10)
以此类推下去,就有
Print(1234)
==>Print(123) + printf(4)
==>Print(12) + printf(3)
==>Print(1) + printf(2)
==>printf(1)
直到被打印的数字变成⼀位数的时候,就不需要再拆分,递归结束。
那么代码就是
void Print(int n)
{if (n > 9)Print(n/10);printf("%d ", n % 10);
}int main()
{int n = 0;scanf("%d", &n);//1234Print(n);return 0;
}
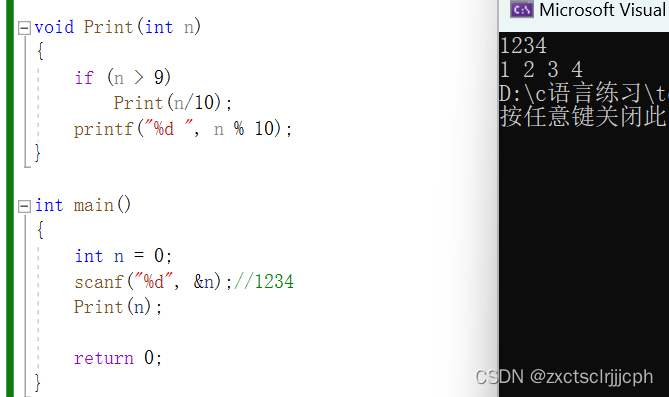
在这个解题的过程中,我们就是使用了大事化小的思路
把Print(1234) 打印1234每一位,拆解为首先Print(123)打印123的每⼀位,再打印得到的4
把Print(123) 打印123每一位,拆解为首先Print(12)打印12的每一位,再打印得到的3
直到Print打印的是一位数,直接打印就行。
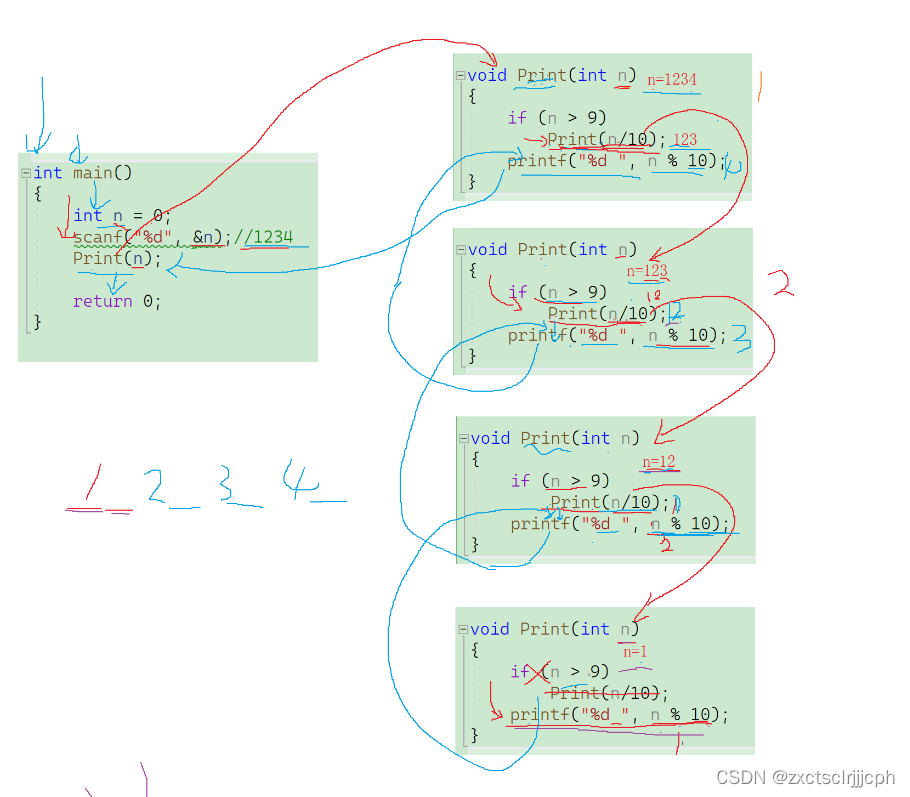
4.2.2 画图推演
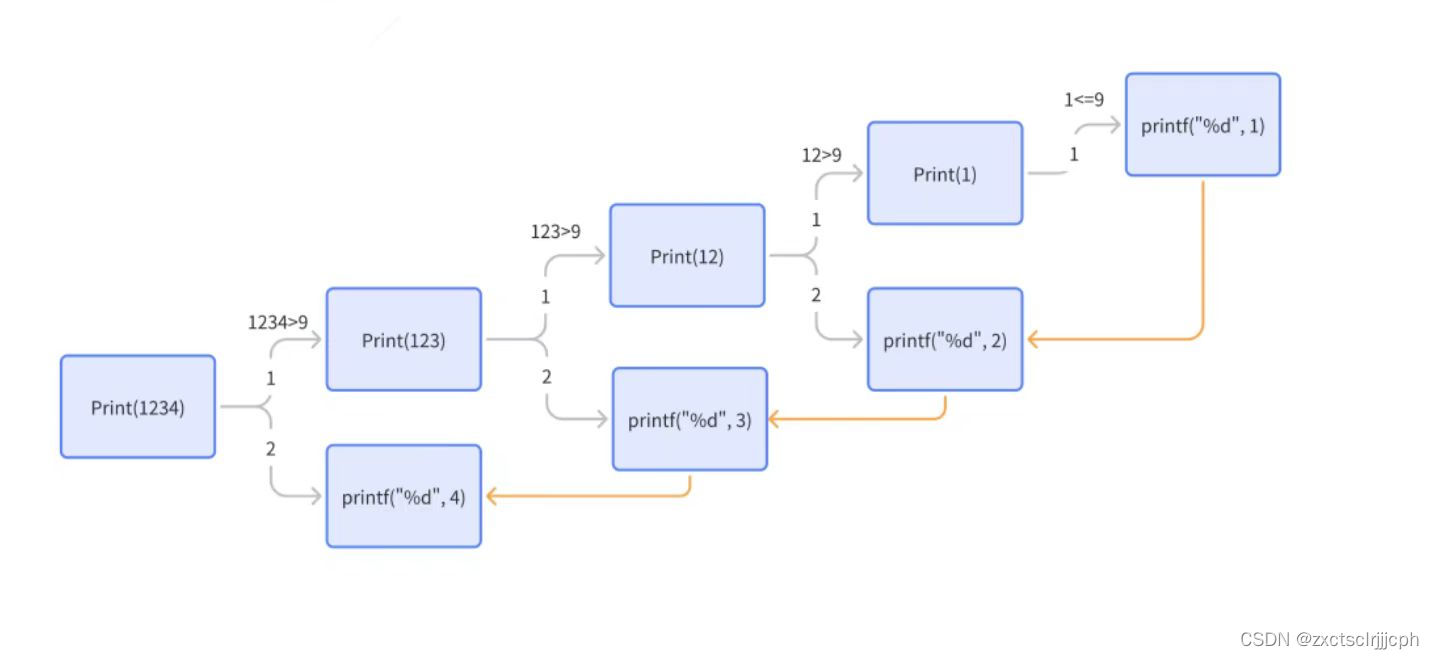
4.3 求第n个斐波那契数
斐波那契数列前两项都是1,后面的是前面两项的和。
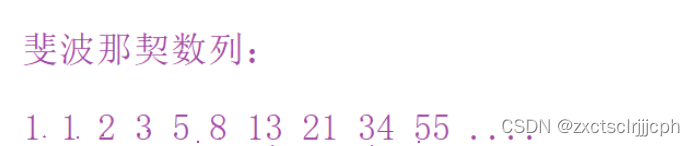
斐波那契数的问题通过是使用递归的形式描述的公式。
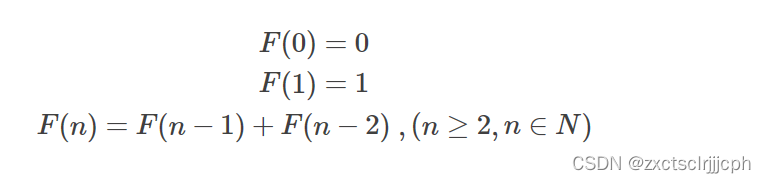
看到这公式,很容易诱导我们将代码写成递归的形式,如下所示:
int Fib(int n)
{if (n <= 2)return 1;elsereturn Fib(n - 1) + Fib(n - 2);
}
int main()
{int n = 0;scanf("%d", &n);int ret = Fib(n);printf("%d\n", ret);return 0;
}
来测试一下:

当我们n输⼊为50的时候,需要很长时间才能算出结果,这个计算所花费的时间,是我们很难接受的,这也说明递归的写法是非常常低效的,那是为什么呢?
要计算50就要先计算49和48,要计算49就要计算48和47,要计算48就要计算47和46,…一直这个下去,浪费时间重复计算。

那么除了递归还有其它的方式吗?
此时就要介绍迭代。
5. 递归与迭代
递归是一种很好的编程技巧,但是很多技巧一样,也是可能被误用的,就像举例1⼀样,看到推导的公式,很容易就被写成递归的形式:
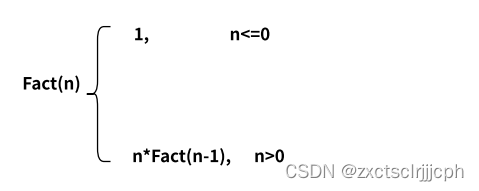
int Fact(int n)
{if(n<=0)return 1;elsereturn n*Fact(n-1);
}
Fact函数是可以产生正确的结果,但是在递归函数调用的过程中涉及一些运行时的开销。
在C语言中每一次函数调用,都要需要为本次函数调用在栈区申请⼀块内存空间来保存函数调用期间的各种局部变量的值,这块空间被称为运行时堆栈,或者函数栈帧。
函数不返回,函数对应的栈帧空间就⼀直占用,所以如果函数调用中存在递归调用的话,每⼀次递归函数调用都会开辟属于自己的栈帧空间,直到函数递归不再继续,开始回归,才逐层释放栈帧空间。
所以如果采用函数递归的方式完成代码,递归层次太深,就会浪费太多的栈帧空间,也可能引起栈溢出(stack over flow)的问题。
所以如果不想使用递归就得想其他的办法,通常就是迭代的方法(通常就是循环的方法)。
比如:计算n的阶乘,也是可以产生1~n的数字累计乘在⼀起的。
int main()
{int n = 0;scanf("%d", &n);int i = 0;int ret = 1;for (i = 1; i <= n; i++){ret = ret * i;}printf("%d\n", ret);return 0;
}
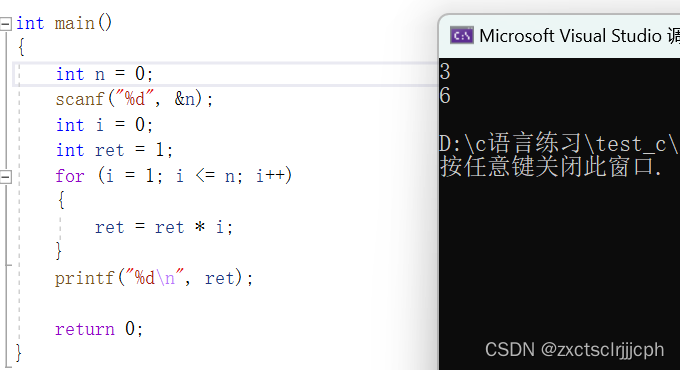
上述代码是能够完成任务,并且效率是比递归的方式更好的。
注意:
- 如果一个问题使用递归的方式去写代码,是非常方便的,简单的写出的代码是没有明显缺陷的,这个时候使用递归就可以
- 如果使用递归写的代码, 是存在明显的缺陷的
比如: 栈溢出, 效率低下等
这时候必须考虑其他方式, 比如:迭代
5.1 迭代求第n个斐波那契数

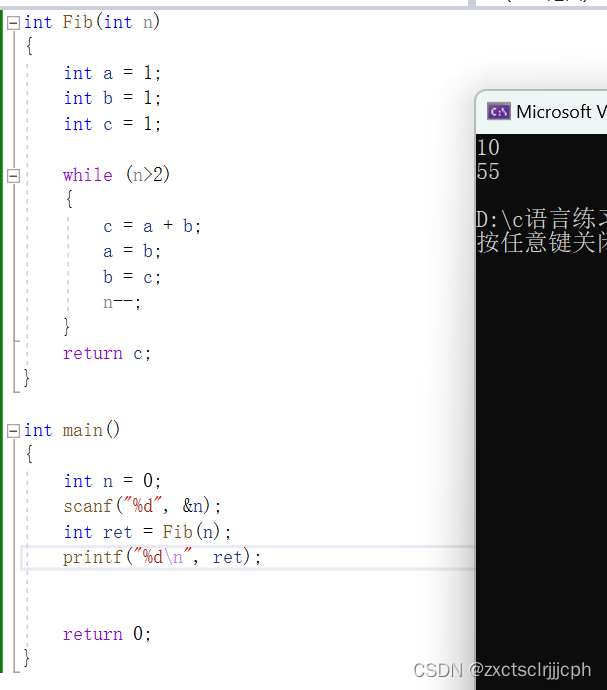
前两个数不需要计算,假设第一个用a记录,第二个用b记录。当n大于2时就要实现前面两个数字,就要相加,然后将a和b都向后挪,也就是将b的值给a,c的值给b,然后再执行a+b,每执行一次n都要减减一下。
int Fib(int n)
{int a = 1;int b = 1;int c = 1;while (n>2){c = a + b;a = b;b = c;n--;}return c;
}int main()
{int n = 0;scanf("%d", &n);int ret = Fib(n);printf("%d\n", ret);return 0;
}
有问题请指出,大家一起进步!
相关文章:

【C语言】递归详解
目录 1.前言2. 递归的定义3. 递归的限制条件4. 递归举例4.1 求n的阶乘4.1.1 分析和代码实现4.1.2 画图演示 4.2 顺序打印一个整数的每一位4.2.1 分析和代码实现4.2.2 画图推演 4.3 求第n个斐波那契数 5. 递归与迭代5.1 迭代求第n个斐波那契数 1.前言 这次博客内容是与递归有关&…...
NSSCTF 文件上传漏洞题目
目录 [SWPUCTF 2021 新生赛]easyupload1.0 [SWPUCTF 2021 新生赛]easyupload2.0 [SWPUCTF 2021 新生赛]easyupload3.0 [SWPUCTF 2021 新生赛]easyupload1.0 这是一个文件上传漏洞的题目 我们的思路是上传一句话木马,用工具进行连接 先编写一句话木马 将文件后缀…...
layui+ssm实现数据表格双击编辑更新数据
layui实现数据表格双击编辑数据更新 在使用layui加载后端数据请求时,对数据选项框进行双击即可实现数据的输入编辑更改 代码块 var form layui.form, table layui.table,layer parent.layer undefined ? layui.layer : parent.layer,laypage layui.laypag…...
windows下DSS界面本地集成linkis管理台
说明:当前开发环境为windows,node版本使用16.15.1。启动web时,确保后端服务已准备就绪。 1.linkis web编译 #进入项目WEB根目录 $ cd linkis/linkis-web #安装项目所需依赖 $ npm install参考官方编译说明,windows下编译一直异常…...
基于PaddleSeg开发的人像抠图web api接口
前言 基于PaddleSeg开发的人像抠图web api接口,提取官方代码,适配各种系统,通过api的接口进行访问。 环境要求 1、Python3.7以上 2、源码(文章最后下载) 源码结构 测试module.py中添加如下代码: if __na…...
Python---面向对象的基本概念
对象 对象,object,现实业务逻辑的一个动作实体就对应着OOP编程中的一个对象! 所以:① 对象使用属性(property)保存数据!② 对象使用方法(method)管理数据! …...

cv2.threshold 图像二值化
图像二值化 whatparameters示例 what cv2.threshold是OpenCV中用于进行图像二值化的函数。它的作用是将输入图像的像素值转换为两个可能的值之一,通常是0(黑色)或255(白色),根据一个设定的阈值。图像二值化…...
CRM:提升营销效果的关键
一场成功的营销活动,可以帮助企业扩大知名度,获取大量的优质商机。作为专业的管理软件,CRM系统同样具备营销管理的能力,帮助企业实现营销活动的规划、执行和监控,提高营销效果。下面说说,CRM营销自动化对企…...

AIGC: 关于ChatGPT中基于API实现一个StreamClient流式客户端
Java版GPT的StreamClient 可作为其他编程语言的参考注意: 下面包名中的 xxx 可以换成自己的代码基于java,来源于网络,可修改成其他编程语言实现参考前文: https://blog.csdn.net/Tyro_java/article/details/134748994 1 )核心代码结构设计 …...
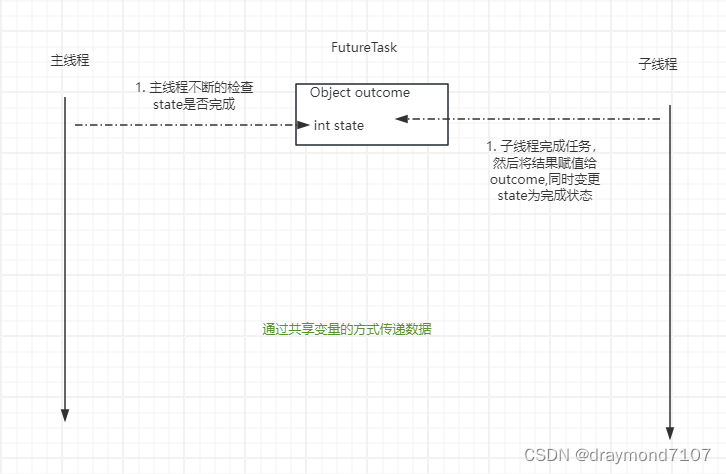
FutureTask
1. 作用 异步操作获取执行结果取消任务执行,判断是否取消执行判断任务执行是否完毕 2. demo public static void main(String[] args) throws Exception {Callable<String> callable () -> search();FutureTask<String> futureTasknew FutureTask&…...
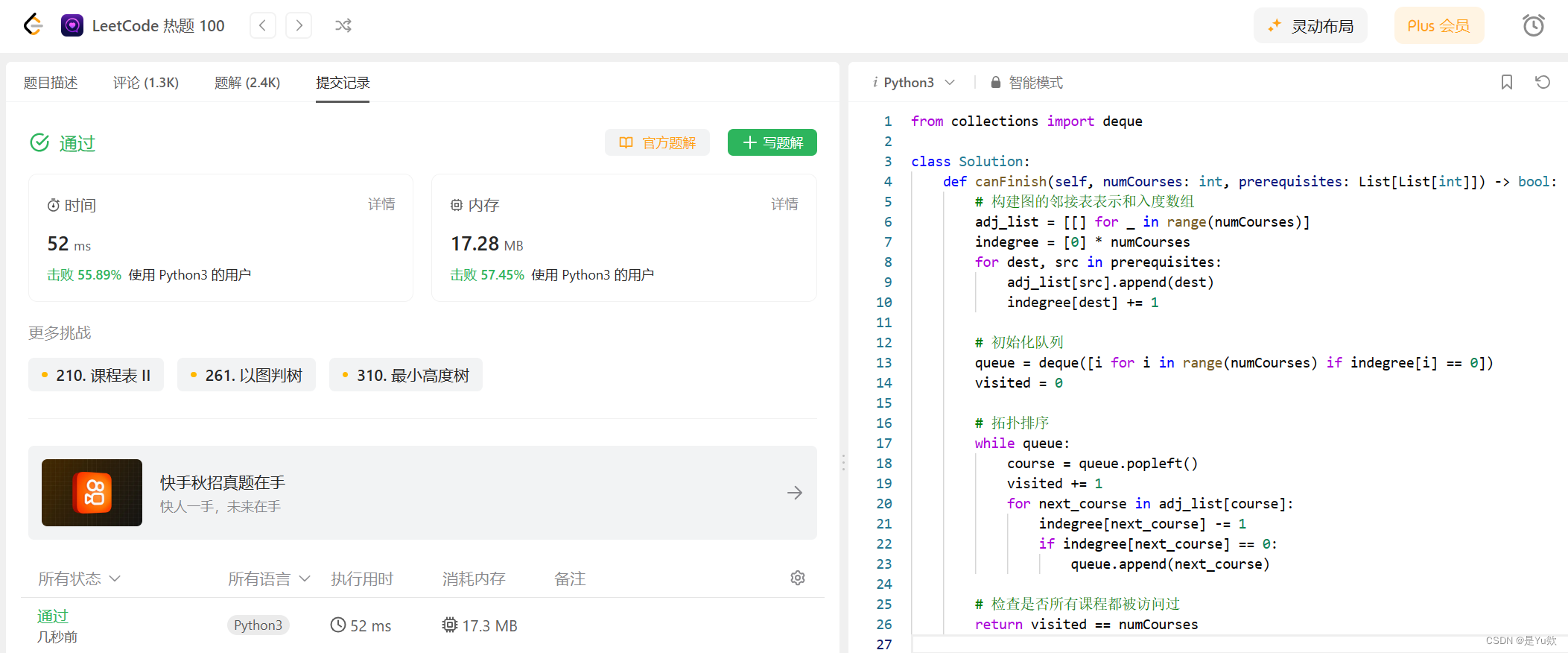
【力扣热题100】207. 课程表 python 拓扑排序
【力扣热题100】207. 课程表 python 拓扑排序 写在最前面207. 课程表解决方案:判断是否可以完成所有课程的学习方法:拓扑排序实现步骤Python 实现性能分析结论 写在最前面 刷一道力扣热题100吧 难度中等 https://leetcode.cn/problems/course-schedule…...

【滑动窗口】LeetCode2953:统计完全子字符串
作者推荐 [二分查找]LeetCode2040:两个有序数组的第 K 小乘积 本题其它解法 【离散差分】LeetCode2953:统计完全子字符串 题目 给你一个字符串 word 和一个整数 k 。 如果 word 的一个子字符串 s 满足以下条件,我们称它是 完全字符串: s 中每个字符…...

base64转PDF
今天做皖事通的对接,下载电子证照后发现回传的是base64,调试确认是个麻烦事,网上搜了一下没有base64转PDF的在线预览功能,只能自己写个调试工具了,以下是通过纯JS方式写的代码,可直接拿去使用: …...

clip-path,css裁剪函数
https://www.cnblogs.com/dzyany/p/13985939.html clip-path - CSS:层叠样式表 | MDN 我们看下这个例子 polygon里有四个值分别代表这四个点相对于原图左上方的偏移量。 裁剪个五角星...

第二证券:食品饮料板块拉升,乳业股亮眼,西部牧业“20cm”涨停
证券时报网讯,食物饮料板块5日盘中拉升走高,乳业股体现活跃,到发稿,骑士乳业涨超27%,西部牧业“20cm”涨停,阳光乳业亦涨停。 其它个股方面,盖世食物涨超20%,润普食物涨超18%&#…...

React 好用的工具库
1、html-react-parser HTML 到 React 解析器,适用于服务器 (Node.js) 和客户端(浏览器),适用于React节点修改过滤等需求 解析器将 HTML 字符串转换为一个或多个 React 元素。可以将一个元素替换为另一个元素…...
C++面试宝典第2题:逆序输出整数
题目 写一个方法,将一个整数逆序打印输出到控制台。注意:当输入的数字含有结尾的0时,输出不应带有前导的0。比如:123的逆序输出为321,8600的逆序输出为68,-609的逆序输出为-906。 解析 这道题本身并没有什么…...
Twincat功能块使用经验总结
控制全局变量: //轴控制指令 bi_Power: BOOL; //使能 bi_Reset: BOOL; //复位 bi_Stop: BOOL; //停止 bi_JogForward: BOOL; //正向点动 bi_JogBackwards: BOOL; //反向点动 bi_MoveAdditive: BOOL; //增量位…...

香港服务器时间不准,差8小时
解决方案1 1、timedatectl查看系统时间 2、查看系统时区 ls /usr/share/zoneinfo 3、删除当前系统所处时区 rm /etc/localtime 4、创建软链接,以替换当前的时区信息 ln -s /usr/share/zoneinfo/Universal /etc/localtime 解决方案2 手动设置硬件时钟 1、设置系…...

C++ 抽象类和接口 详解
目录 0 引言1 抽象类2 接口2.1 Java与C接口的区别 🙋♂️ 作者:海码007📜 专栏:C专栏💥 标题:C 抽象类和接口 详解❣️ 寄语:书到用时方恨少,事非经过不知难!…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...
