成为AI产品经理——回归模型评估(MSE、RMSE、MAE、R方)
分类问题的评估是看实际类别和预测类别是否一致,它的评估指标主要有混淆矩阵、AUC、KS。回归问题的评估是看实际值和预测值是否一致,它的评估指标包括MAE、MSE、RMSE、R方。
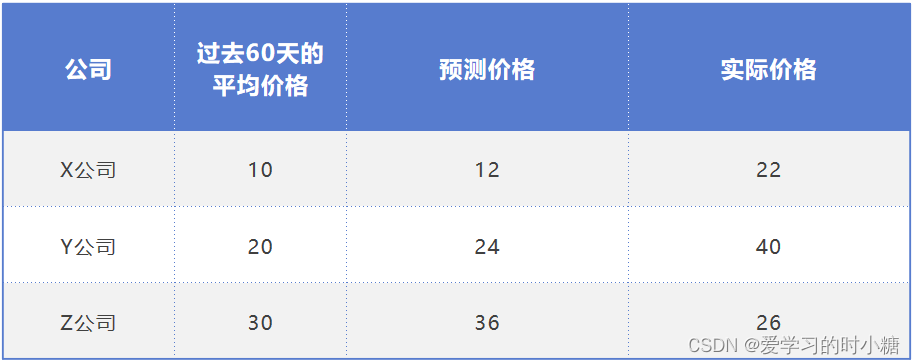
如果我们预测第二天某支股票的价格,给一个模型 y=1.5x,x是最近60天股票的价格的平均值,y是预测的第二天股票的结果。我们选择三支股票,记录它过去60天的均价,以及模型预测出来的价格和实际的价格。
下面的图片是将过去60天股票均价作为X轴,将股票价格作为Y轴做出的散点图。

我们想要算出预测和实际结果的差异,最原本的方法是直接将每一个样本的预测值和实际值做差,再将所有的差值结果进行相加。
它们的差值情况分别为:22-12=10,40-24=16,26-36=-10。可以看到Z公司的差值为-10,它与其他的差值相加会造成抵消误差的情况,所以这种方法不合理。
为了避免差值相互抵消的情况,我们将差值的平方相加。
这种计算误差的方式在会受到样本个数的影响,在样本比较少的情况下它的误差会比较小,样本比较多的话,误差会较大。为了避免这种情况的出现,我们将平方和计算出来的误差除以样本个数就可以不受样本个数的影响,这种计算误差的方式我们称为均方误差。
一、MSE(均方误差)
其中n:样本数量 :表示实际值
:表示预测值
计算方式就是:样本的实际值和样本预测值差值的平方再除以样本数量。
这个值一定是大于等于0的,我们在评估的时候应该让这个值越小越好。
二、RMSE(均方根误差)
在使用均方误差对于值取平方的时候,会导致量纲发生变化,比如:我们计算的是米,但是平方之后是平方米,为了保持量纲一致,我们再对它开方,也就是均方根误差。
这个数值结果也是越小越好的。
三、MAE(绝对平均值)
我们将差值取平方的原因是为了避免正负抵消操作,我们还可以使用差值取绝对值的方式来避免抵消,计算误差。
这个数值结果也是越小越好。
四、R方
在模型预测过程中,我们可能会想用同一个模型解决不同得问题。由于预测样本不一致,最终的预测结果可能会随着量纲的差异上至几万,下至几百。为了避免这种情况的出现,将误差使用0-1的概率表示出来,我们使用R方的计算公式。
是实际结果和预测值之间相关系数的平方。
TSS:表示总离差平方和。就是实际值和实际值均值的差值平方和。
RSS:表示残差平方和。实际值和预测值之间的差值平方和。
它的值一般在0-1的范围内,越靠近1,说明模型预测的越准确。
我们继续使用上面股票预测的例子来说明这个R方的计算方法。

第一步:求实际值均值:
第二步:
第三步:
第四步:带入公式,
五、误差公式选择
均方误差会进行差值平方,有一个数据放大的过程。均方根误差虽然平方再开方,但是还是会比实际的误差大,所以我们一般想要更接近误差的数据,选择MAE。
对于算法工程师而言,将误差放大有利于他们发现误差。算法工程师一般会选择MSE和RMSE。
六、总结

1.想获得更加真实的误差结果选择MAE,想要找到更明确的误差选择MSE。
2.如果想要将一个模型应用解决不同的问题时,选择可以看到模型在那个问题上表现得更好。
参考文献:刘海丰——《成为AI产品经理》 自用,请勿传播
相关文章:
成为AI产品经理——回归模型评估(MSE、RMSE、MAE、R方)
分类问题的评估是看实际类别和预测类别是否一致,它的评估指标主要有混淆矩阵、AUC、KS。回归问题的评估是看实际值和预测值是否一致,它的评估指标包括MAE、MSE、RMSE、R方。 如果我们预测第二天某支股票的价格,给一个模型 y1.5x,…...

【C++11(一)】右值引用以及列表初始化
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 C11 1. 前言2. 统一的列表初始化3. initializer…...

通俗理解Jenkins是什么?
目录 通俗理解 Jenkins是什么? 通俗理解 假设你有一个软件项目,多个开发者在一起写代码。每当有人提交新的代码时,你想要自动地构建、测试这些代码,确保它们没有引入问题。 Jenkins就像一个聪明的助手,会在有人提交…...
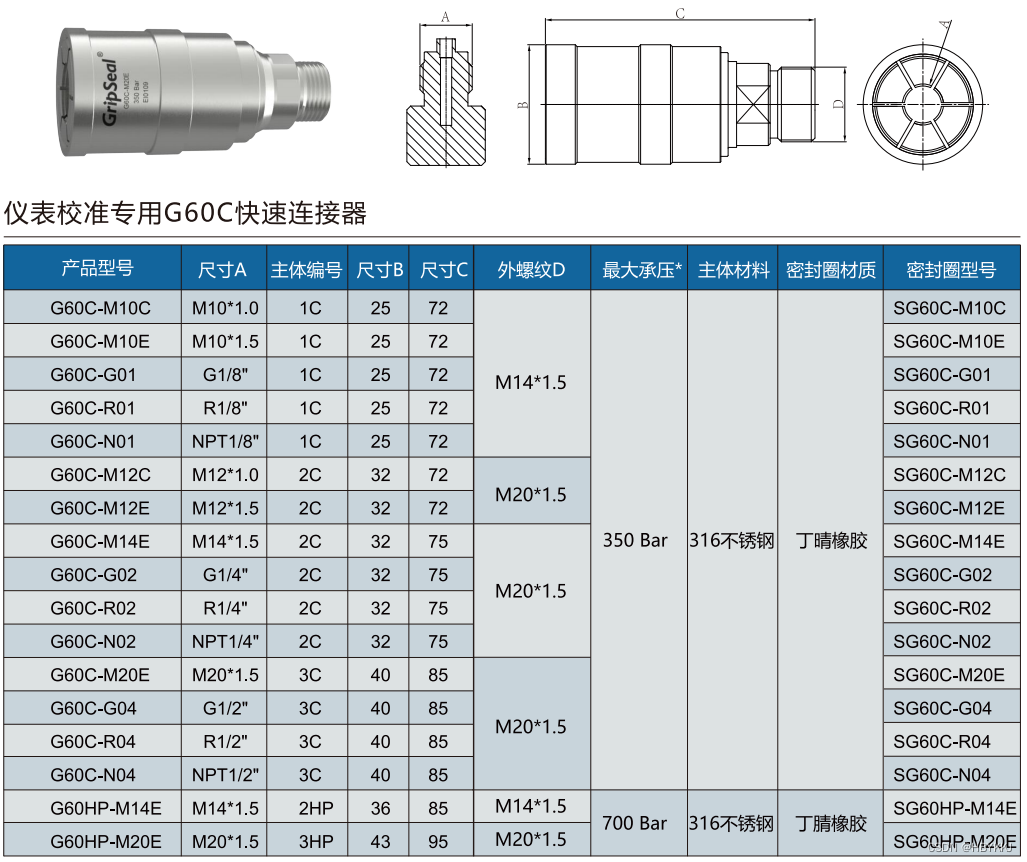
格雷希尔帮助仪器仪表测试时快速密封的G60C系列接头其优势有哪些
仪器仪表在工业领域中扮演着重要的角色,如:压力表,压力传感器、压力变送器、压力开关、压力歧管等这些,在工业领域中都是随处可见的,其数据的精度直接影响着产品在生产过程中的质量和安全性;因此࿰…...

系统运维工具KSysAK——让运维回归简单
系统运维工具KSysAK——让运维回归简单 1.基本信息 1.1概述 系统异常定位分析工具KSysAK是云峦操作系统研发及运维人员总结开发及运维经验,设计和研发的多个运维工具的集合,可以覆盖系统的日常监控、线上问题诊断和系统故障修复等常见运维场景。 工具…...
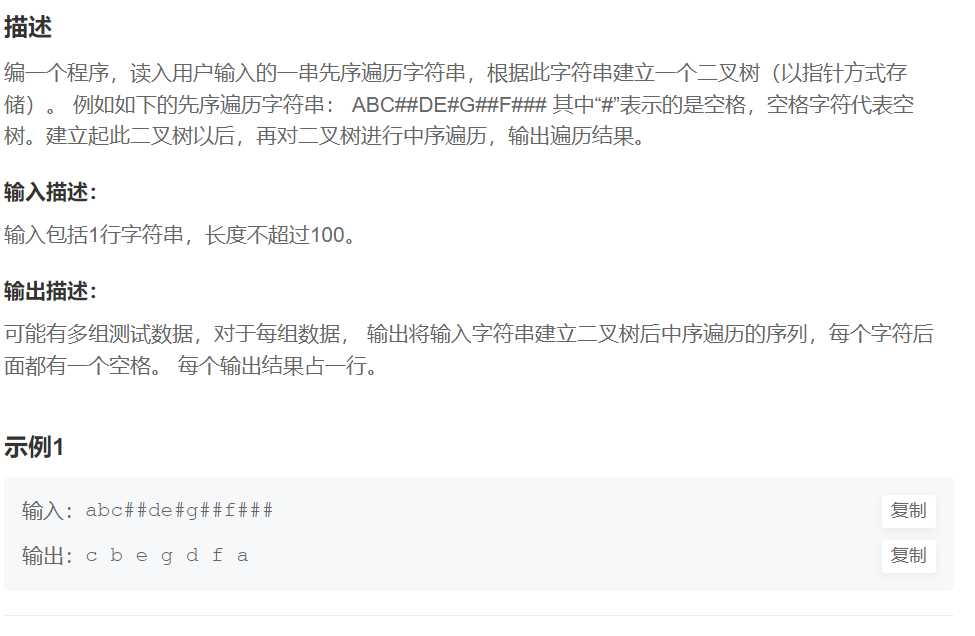
NowCoder | KY11 二叉树遍历
NowCoder | KY11 二叉树遍历 OJ链接 简单来说就是构建这个二叉树定义结构体通过递归方式根据输入的字符串构建二叉树。对于输入字符串中的每个字符,如果是 ‘#’ 表示空节点,否则创建一个新节点,并递归地构建左右子树。 #include <limit…...

android.view.WindowLeaked解决方法
问题 我在使用WindowManager添加一个button, windowManager.addView(button,layoutParams);然后关闭当前的这个Activity的时候遇到了WindowLeak这个问题,也就是所谓的窗体泄露。 原因 主要原因是因为android只允许在UI主线程操作,我在使用W…...
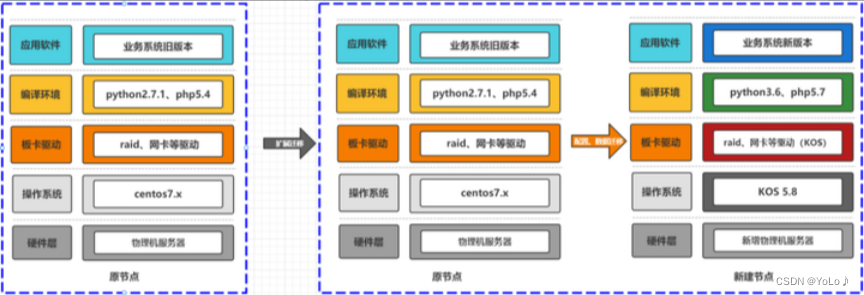
浪潮信息KeyarchOS的飞跃之路
1.背景 在正式向大家介绍KOS之前,我们先关注这样一些问题。 传统操作系统在大规模数据处理、高性能计算和人工智能应用方面面临着一些瓶颈问题,包括存储和访问效率、数据传输和通信效率、并行计算性能等等问题。为了能够更好的改进这些问题,…...

C++基础 -41- 迭代器
每个stl 模板接口都有一个专用的迭代器 迭代器就是 stl 库中的 一个特殊指针,功能与指针类似(类似但不是) 迭代器定义格式 迭代器的使用,使用迭代器遍历向量容器的参数 代码运行结果 无论使用普通方式还是迭代器方式去都可以遍历vector容器...
zookeeper心跳检测 (实操课程)
本系列是zookeeper相关的实操课程,课程测试环环相扣,请按照顺序阅读来学习和测试zookeeper。 阅读本文之前,请先阅读----zookeeper 单机伪集群搭建简单记录(实操课程系列)zookeeper 客户端常用命令简单记录…...

社区新零售:重塑零售业的全新模式
社区新零售:重塑零售业的全新模式 近年来,新零售业成为了研究的焦点,它是一种以互联网为基础的零售形式。新零售通过运用先进技术手段,如大数据和人工智能,对商品的生产、流通和销售过程进行升级改造,重新构…...

北京华联BHGMall“宠粉模式”不断迭代,强体验注互动成行业UP主
在今年双11热度遇冷后,双十二被官宣取消,而这背后本质已经间接印证:传统“电商大促”的模式,已经难以为继。反观线下消费市场,则是以持续恢复和增长成为经济恢复的亮点,从线下客流量的快速回升,…...
前端时间的失败总结复盘
分享失败经验,前段时间的总结复盘: 与伙伴合作面对异常决策要及时提出质疑,怼,别太客气,客气起来,小心翼翼在意他人情绪那么这个项目就会让人难受,不要因为因为伙伴身上有标签/光环/权威就觉得…...

Ribbon 负载均衡
1、负载均衡整体流程 2、负载均衡流程逐级跟踪运行 (1) LoadBlanced 注解可以使LoadBalancerInterceptor拦截到; (2)LoadBalancerInterceptor 实现了ClientHttpRequestInterceptor接口; (3)ClientHttpRequestInterceptor接口释义如下; (4)int…...

微服务实战系列之Cache(技巧篇)
前言 凡工具必带使用说明书,如不合理的使用,可能得到“意外收获”。这就好比每个人擅长的领域有所差异,如果放错了位置或用错了人,也一定会让 Leader 们陷入两难之地:“上无法肩负领导之重托,下难免失去伙伴…...

6.17验证二叉树(LC98-M)
算法: 中序遍历下,输出的二叉搜索树节点的数值是有序序列。 有了这个特性,验证二叉搜索树,就相当于变成了判断一个序列是不是递增的了。 具体地:中序遍历时,判断当前节点是否大于中序遍历的前一个节点&a…...
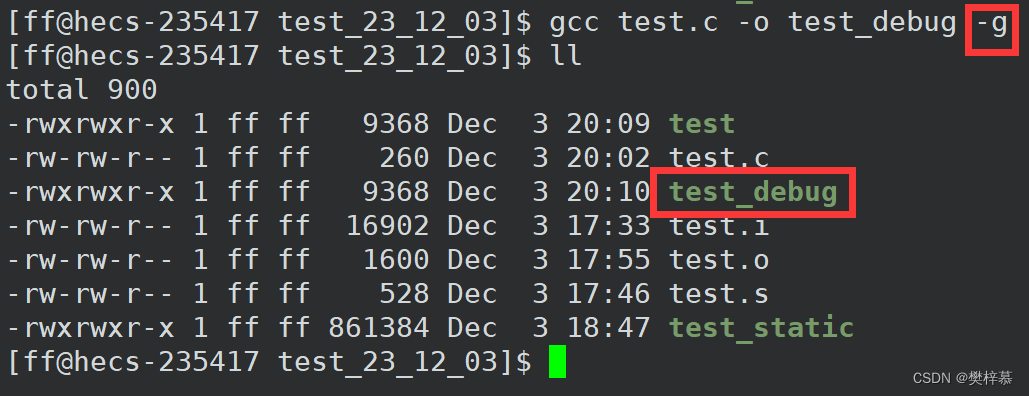
【Linux】编译器-gcc/g++与调试器-gdb的使用
👀樊梓慕:个人主页 🎥个人专栏:《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》《C》《Linux》 🌝每一个不曾起舞的日子,都是对生命的辜负 目录 前言 1.gcc/g语法 2.gcc的使用及…...

Google Guava 散列工具使用详解
文章目录 散列哈希函数哈希码布隆过滤器 散列 Guava 提供了一组散列(哈希)相关的工具类和方法,包括哈希函数接口、哈希算法实现、哈希码(HashCode)类、布隆过滤器(BloomFilter)等等。 Guava 提…...
AIGC-文生视频
stable diffusion的前传: 轻松理解 VQ-VAE:首个提出 codebook 机制的生成模型 - 知乎近两年,有许多图像生成类任务的前沿工作都使用了一种叫做"codebook"的机制。追溯起来,codebook机制最早是在VQ-VAE论文中提出的。相比…...

java中Collectors.groupingBy返回实例?
在Java中,Collectors.groupingBy()是一个用于对流元素进行分组的收集器。它可以根据指定的分类函数对流元素进行分组,并返回一个Map对象,其中键是分组的标准,值是属于相应组的元素列表。 下面是一个使用Collectors.groupingBy()方…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
