1. 小游戏(贪心)
题干:
谷同学很喜欢玩计算机游戏,特别是战略游戏,但是有时他不能尽快找到解所以常常感到很沮丧。现在面临如下问题:他必须在一个中世纪的城堡里设防,城堡里的道路形成一棵无向树。要在结点上安排最少的士兵使得他们可以看到所有边。你能帮助他吗?
你的任务是给出士兵的最少数目。
输入:包含多组数据。每组数据表示一棵树,在每组数据中:
第一行是结点的数目。
接下来的几行,每行按如下格式描述一个结点:结点标识符 : ( 道路的数目 ) 结点标识符1 结点标识符2 ...... 结点标识符道路的数目
或者
结点标识符 : (0)
对于 n (0<n<=1500) 个结点,结点标识符是一个从 0 到 n - 1 的整数。每条边在测试用例中只出现一次。
对于每组数据,各给出一个整数表示士兵的最少数目。
| 测试输入 | 期待的输出 | 时间限制 | 内存限制 | 额外进程 | |
|---|---|---|---|---|---|
| 测试用例 1 | 以文本方式显示
| 以文本方式显示
| 1秒 | 64M | 0 |
代码如下:
这里和小学期的知识对应起来了。(动态规划dp[n][2]的设计)
#include <iostream>
#include <cstring>
using namespace std;const int MAXN = 1505;
int dp[MAXN][2], visited[MAXN], link[MAXN][MAXN];
void DFS(int root)
{visited[root] = 1;for (int i = 0; link[root][i] != -1; ++i){int m = link[root][i];if (!visited[m]){DFS(m);dp[root][1] += dp[m][0];dp[root][0] += min(dp[m][0], dp[m][1]);}}dp[root][0]++;
}
int main()
{int n;while (scanf("%d", &n) != EOF){memset(dp, 0, sizeof(dp));memset(visited, 0, sizeof(visited));memset(link, 0, sizeof(link));int node, next, temp, root;for (int i = 0; i < n; i++){scanf("%d:(%d)", &node, &next);root = (!i) ? node : root;int j = 0;for (; j < next; ++j){cin >> temp;link[node][j] = temp;}link[node][j] = -1;}DFS(root);cout << min(dp[root][0], dp[root][1]) << endl;}return 0;
}相关文章:
)
1. 小游戏(贪心)
题干: 谷同学很喜欢玩计算机游戏,特别是战略游戏,但是有时他不能尽快找到解所以常常感到很沮丧。现在面临如下问题:他必须在一个中世纪的城堡里设防,城堡里的道路形成一棵无向树。要在结点上安排最少的士兵使得他们可以…...

记录 | c++打印变量类型
c打印变量类型: 使用 typeid(变量名).name() int main(){std::cout << "type of ss : " << typeid(ss).name() << std::endl; }...
nodejs_vue+vscode美容理发店会员管理系统un1dm
按照设计开发一个系统的常用流程来描述系统,可以把系统分成分析阶段,设计阶段,实现阶段,测试阶段。所以在编写系统的说明文档时,根据系统所处的阶段来描述系统的内容。 绪论:这是对选题的背景,意…...
C语言 操作符详解
C语言学习 目录 文章目录 前言 一、算术操作符 二、移位操作符 2.1 左移操作符 2.2 右移操作符 三、位操作符 3.1 按位与操作符 & 3.2 按位或操作符 | 3.3 按位异或操作符 ^ 四、赋值操作符 五、单目操作符 5.1 逻辑反操作符! 5.2 正值、负值-操作符 5.3 取地址…...
成为AI产品经理——回归模型评估(MSE、RMSE、MAE、R方)
分类问题的评估是看实际类别和预测类别是否一致,它的评估指标主要有混淆矩阵、AUC、KS。回归问题的评估是看实际值和预测值是否一致,它的评估指标包括MAE、MSE、RMSE、R方。 如果我们预测第二天某支股票的价格,给一个模型 y1.5x,…...

【C++11(一)】右值引用以及列表初始化
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 C11 1. 前言2. 统一的列表初始化3. initializer…...

通俗理解Jenkins是什么?
目录 通俗理解 Jenkins是什么? 通俗理解 假设你有一个软件项目,多个开发者在一起写代码。每当有人提交新的代码时,你想要自动地构建、测试这些代码,确保它们没有引入问题。 Jenkins就像一个聪明的助手,会在有人提交…...
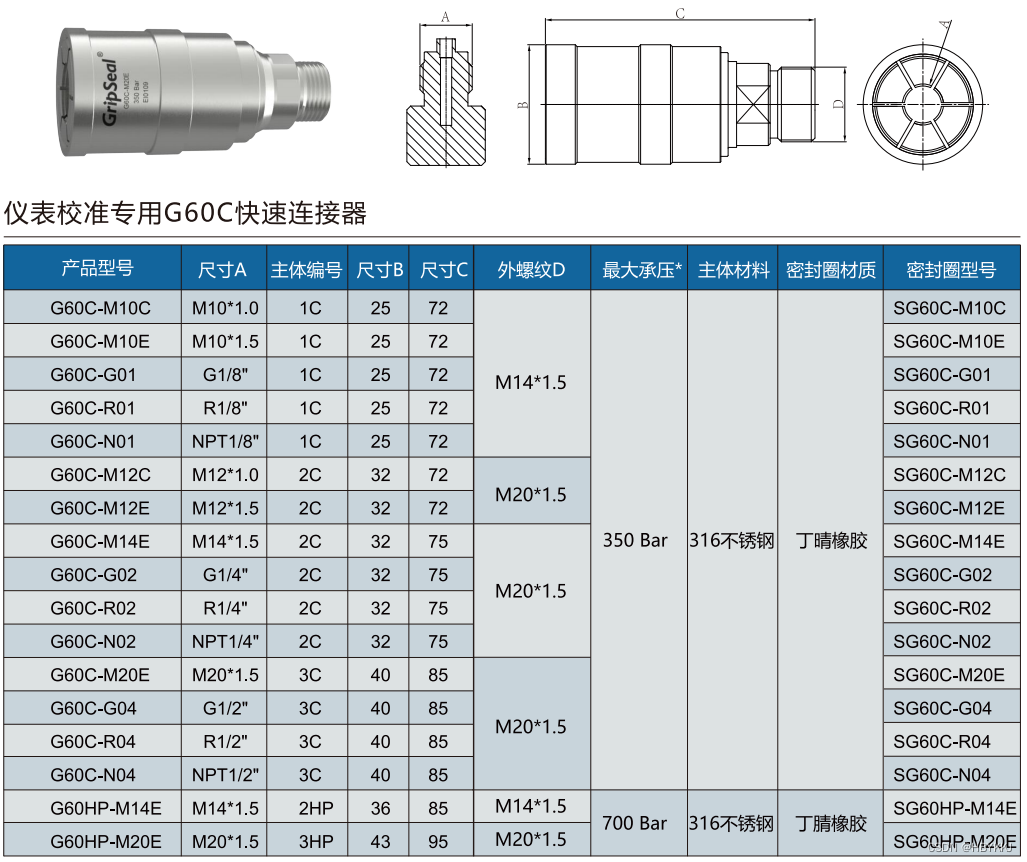
格雷希尔帮助仪器仪表测试时快速密封的G60C系列接头其优势有哪些
仪器仪表在工业领域中扮演着重要的角色,如:压力表,压力传感器、压力变送器、压力开关、压力歧管等这些,在工业领域中都是随处可见的,其数据的精度直接影响着产品在生产过程中的质量和安全性;因此࿰…...

系统运维工具KSysAK——让运维回归简单
系统运维工具KSysAK——让运维回归简单 1.基本信息 1.1概述 系统异常定位分析工具KSysAK是云峦操作系统研发及运维人员总结开发及运维经验,设计和研发的多个运维工具的集合,可以覆盖系统的日常监控、线上问题诊断和系统故障修复等常见运维场景。 工具…...
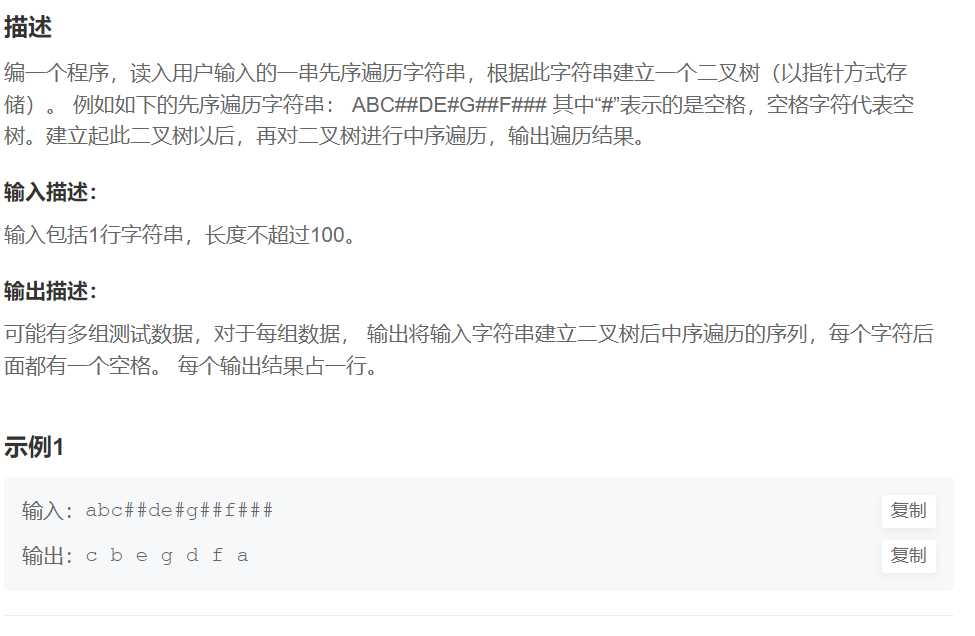
NowCoder | KY11 二叉树遍历
NowCoder | KY11 二叉树遍历 OJ链接 简单来说就是构建这个二叉树定义结构体通过递归方式根据输入的字符串构建二叉树。对于输入字符串中的每个字符,如果是 ‘#’ 表示空节点,否则创建一个新节点,并递归地构建左右子树。 #include <limit…...

android.view.WindowLeaked解决方法
问题 我在使用WindowManager添加一个button, windowManager.addView(button,layoutParams);然后关闭当前的这个Activity的时候遇到了WindowLeak这个问题,也就是所谓的窗体泄露。 原因 主要原因是因为android只允许在UI主线程操作,我在使用W…...
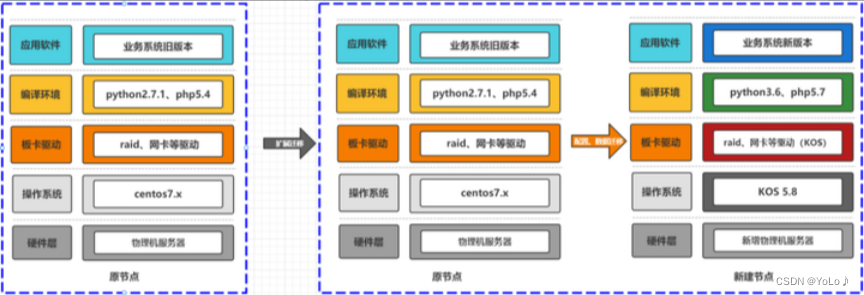
浪潮信息KeyarchOS的飞跃之路
1.背景 在正式向大家介绍KOS之前,我们先关注这样一些问题。 传统操作系统在大规模数据处理、高性能计算和人工智能应用方面面临着一些瓶颈问题,包括存储和访问效率、数据传输和通信效率、并行计算性能等等问题。为了能够更好的改进这些问题,…...

C++基础 -41- 迭代器
每个stl 模板接口都有一个专用的迭代器 迭代器就是 stl 库中的 一个特殊指针,功能与指针类似(类似但不是) 迭代器定义格式 迭代器的使用,使用迭代器遍历向量容器的参数 代码运行结果 无论使用普通方式还是迭代器方式去都可以遍历vector容器...
zookeeper心跳检测 (实操课程)
本系列是zookeeper相关的实操课程,课程测试环环相扣,请按照顺序阅读来学习和测试zookeeper。 阅读本文之前,请先阅读----zookeeper 单机伪集群搭建简单记录(实操课程系列)zookeeper 客户端常用命令简单记录…...

社区新零售:重塑零售业的全新模式
社区新零售:重塑零售业的全新模式 近年来,新零售业成为了研究的焦点,它是一种以互联网为基础的零售形式。新零售通过运用先进技术手段,如大数据和人工智能,对商品的生产、流通和销售过程进行升级改造,重新构…...

北京华联BHGMall“宠粉模式”不断迭代,强体验注互动成行业UP主
在今年双11热度遇冷后,双十二被官宣取消,而这背后本质已经间接印证:传统“电商大促”的模式,已经难以为继。反观线下消费市场,则是以持续恢复和增长成为经济恢复的亮点,从线下客流量的快速回升,…...
前端时间的失败总结复盘
分享失败经验,前段时间的总结复盘: 与伙伴合作面对异常决策要及时提出质疑,怼,别太客气,客气起来,小心翼翼在意他人情绪那么这个项目就会让人难受,不要因为因为伙伴身上有标签/光环/权威就觉得…...

Ribbon 负载均衡
1、负载均衡整体流程 2、负载均衡流程逐级跟踪运行 (1) LoadBlanced 注解可以使LoadBalancerInterceptor拦截到; (2)LoadBalancerInterceptor 实现了ClientHttpRequestInterceptor接口; (3)ClientHttpRequestInterceptor接口释义如下; (4)int…...

微服务实战系列之Cache(技巧篇)
前言 凡工具必带使用说明书,如不合理的使用,可能得到“意外收获”。这就好比每个人擅长的领域有所差异,如果放错了位置或用错了人,也一定会让 Leader 们陷入两难之地:“上无法肩负领导之重托,下难免失去伙伴…...

6.17验证二叉树(LC98-M)
算法: 中序遍历下,输出的二叉搜索树节点的数值是有序序列。 有了这个特性,验证二叉搜索树,就相当于变成了判断一个序列是不是递增的了。 具体地:中序遍历时,判断当前节点是否大于中序遍历的前一个节点&a…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
