【数据结构(七)】查找算法
文章目录
- 查找算法介绍
- 1. 线性查找算法
- 2. 二分查找算法
- 2.1. 思路分析
- 2.2. 代码实现
- 2.3. 功能拓展
- 3. 插值查找算法
- 3.1. 前言
- 3.2. 相关概念
- 3.3. 实例应用
- 4. 斐波那契(黄金分割法)查找算法
- 4.1. 斐波那契(黄金分割法)原理
- 4.2. 实例应用
查找算法介绍
在 java 中,我们常用的查找有四种:
① 顺序(线性)查找
② 二分查找/折半查找
③ 插值查找
④ 斐波那契查找
1. 线性查找算法
问题:
数组arr[] = {1, 9, 11, -1, 34, 89},使用线性查找方式,找出11所在的位置。
代码实现:
package search;public class SeqSearch {public static void main(String[] args) {int arr[] = { 1, 9, 11, -1, 34, 89 };// 没有顺序的数组int index = seqSearch(arr, 11);if (index == -1) {System.out.println("没有找到");} else {System.out.println("找到了,下标为:" + index);}}/*** 这里实现的线性查找是找到一个满足条件的值,就返回* * @param arr* @param value* @return*/public static int seqSearch(int[] arr, int value) {// 线性查找是逐一比对,发现有相同的值,就返回下标for (int i = 0; i < arr.length; i++) {if (arr[i] == value) {return i;}}return -1;}}
运行结果:

2. 二分查找算法
问题:
请对一个有序数组进行二分查找 {1,8, 10, 89, 1000, 1234} ,输入一个数看看该数组是否存在此数,并且求出下标,如果没有就提示"没有这个数"。
2.1. 思路分析
二分查找的思路分析
-
首先,确定该数组的中间的下标: m i d = ( l e f t + r i g h t ) / 2 mid = (left + right) / 2 mid=(left+right)/2
-
然后让需要查找的数
findVal和arr[mid]比较
2.1.findVal > arr[mid],说明你要查找的数在mid的右边, 因此需要递归的向右查找
2.2.findVal < arr[mid],说明你要查找的数在mid的左边, 因此需要递归的向左查找
2.3.findVal == arr[mid],说明找到,就返回 -
什么时候需要结束递归:
①找到就结束递归
②递归完整个数组,仍然没有找到findVal,也需要结束递归 当left > right就需要退出
2.2. 代码实现
注意:使用二分查找的前提是 该数组是有序的
package search;public class BinarySearch {public static void main(String[] args) {int arr[] = { 1, 8, 10, 89, 1000, 1234 };int resIndex = binarySearch(arr, 0, arr.length - 1, 1);System.out.println("resIndex= " + resIndex);}// 二分查找法/*** * @param arr 数组* @param left 左边的索引* @param right 右边的索引* @param findVal 要查找的值* @return 如果找到就返回下标,如果没有找到就返回-1*/public static int binarySearch(int[] arr, int left, int right, int findVal) {// 当left > right 时,说明递归整个数组,但是没有找到if (left > right) {return -1;}int mid = (left + right) / 2;int midVal = arr[mid];if (findVal > midVal) {// 向右递归return binarySearch(arr, mid + 1, right, findVal);} else if (findVal < midVal) {return binarySearch(arr, left, mid - 1, findVal);} else {return mid;}}}
运行结果:

2.3. 功能拓展
问题:
数组{1,8, 10, 89, 1000, 1000,1234}, 当一个有序数组中,有多个相同的数值时,如何将所有的数值都查找到,比如这里的 1000。
代码实现:
package search;import java.util.ArrayList;
import java.util.List;public class BinarySearch {public static void main(String[] args) {int arr[] = { 1, 8, 10, 89, 1000, 1000, 1234 };List<Integer> resIndexList = binarySearch2(arr, 0, arr.length - 1, 1000);System.out.println("resIndexList = " + resIndexList);}/** 思路分析:* 1. 在找 mid 的索引值,不要马上返回* 2. 向 mid 索引值的左边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 3. 向 mid 索引值的右边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 4. 将 ArrayList 返回*/public static List<Integer> binarySearch2(int[] arr, int left, int right, int findVal) {// 当left > right 时,说明递归整个数组,但是没有找到if (left > right) {return new ArrayList<Integer>();}int mid = (left + right) / 2;int midVal = arr[mid];if (findVal > midVal) {// 向右递归return binarySearch2(arr, mid + 1, right, findVal);} else if (findVal < midVal) {return binarySearch2(arr, left, mid - 1, findVal);} else {/** 思路分析:* 1. 在找 mid 的索引值,不要马上返回* 2. 向 mid 索引值的左边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 3. 向 mid 索引值的右边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 4. 将 ArrayList 返回*/List<Integer> resIndexlist = new ArrayList<Integer>();// 向 mid 索引值的左边扫描,将所有满足1000的元素的下标,加入到集合ArrayListint temp = mid - 1;while (true) {if (temp < 0 || arr[temp] != findVal) {// 退出break;}// 否则,就将temp放入到resIndexlistresIndexlist.add(temp);temp -= 1;// temp左移}resIndexlist.add(mid);// 向 mid 索引值的右边扫描,将所有满足1000的元素的下标,加入到集合ArrayListtemp = mid + 1;while (true) {if (temp > arr.length - 1 || arr[temp] != findVal) {// 退出break;}// 否则,就将temp放入到resIndexlistresIndexlist.add(temp);temp += 1;// temp左移}return resIndexlist;}}}
运行结果:

3. 插值查找算法
3.1. 前言
二分查找算法存在查找效率较慢的情况,因为其中的mid是从中间开始取的。假如对数组{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 }进行查找,查找 1 所在的位置,实现代码如下:
package search;import java.util.ArrayList;
import java.util.List;public class BinarySearch {public static void main(String[] args) {int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 };List<Integer> resIndexList = binarySearch2(arr, 0, arr.length - 1, 1);System.out.println("resIndexList = " + resIndexList);}/** 思路分析:* 1. 在找 mid 的索引值,不要马上返回* 2. 向 mid 索引值的左边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 3. 向 mid 索引值的右边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 4. 将 ArrayList 返回*/public static List<Integer> binarySearch2(int[] arr, int left, int right, int findVal) {System.out.println("调用了一次");// 当left > right 时,说明递归整个数组,但是没有找到if (left > right) {return new ArrayList<Integer>();}int mid = (left + right) / 2;int midVal = arr[mid];if (findVal > midVal) {// 向右递归return binarySearch2(arr, mid + 1, right, findVal);} else if (findVal < midVal) {return binarySearch2(arr, left, mid - 1, findVal);} else {/** 思路分析:* 1. 在找 mid 的索引值,不要马上返回* 2. 向 mid 索引值的左边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 3. 向 mid 索引值的右边扫描,将所有满足1000的元素的下标,加入到集合ArrayList* 4. 将 ArrayList 返回*/List<Integer> resIndexlist = new ArrayList<Integer>();// 向 mid 索引值的左边扫描,将所有满足1000的元素的下标,加入到集合ArrayListint temp = mid - 1;while (true) {if (temp < 0 || arr[temp] != findVal) {// 退出break;}// 否则,就将temp放入到resIndexlistresIndexlist.add(temp);temp -= 1;// temp左移}resIndexlist.add(mid);// 向 mid 索引值的右边扫描,将所有满足1000的元素的下标,加入到集合ArrayListtemp = mid + 1;while (true) {if (temp > arr.length - 1 || arr[temp] != findVal) {// 退出break;}// 否则,就将temp放入到resIndexlistresIndexlist.add(temp);temp += 1;// temp左移}return resIndexlist;}}}
运行结果:
总共调用了4次才查找出1的索引值,效率较慢。通过插值查找可改善上述问题。
3.2. 相关概念
原理介绍:
插值查找算法类似于二分查找,不同的是插值查找每次从自适应 mid 处开始查找。
mid的计算公式:
对二分查找中的求 mid 索引的公式进行修改:

上图公式中:
① low 表示左边索引 left
② high 表示右边索引 right
③ key 就是前面二分查找中讲的 findVal(要查找的值)
即插值查找的 mid计算公式:
m i d = l o w + ( h i g h − l o w ) k e y − a r r [ l o w ] a r r [ h i g h ] − a r r [ l o w ] \begin{aligned} &mid = low + (high-low)\frac{key-arr[low]}{arr[high]-arr[low]} \end{aligned} mid=low+(high−low)arr[high]−arr[low]key−arr[low]
对应前面的代码公式,即:
m i d = l e f t + ( r i g h t – l e f t ) f i n d V a l – a r r [ l e f t ] a r r [ r i g h t ] – a r r [ l e f t ] \begin{aligned} &mid = left + (right – left)\frac{findVal – arr[left]}{arr[right] – arr[left]} \end{aligned} mid=left+(right–left)arr[right]–arr[left]findVal–arr[left]
举例说明:
数组 arr = [1, 2, 3, …, 100]
①假如需要查找的值是 1
(使用二分查找的话,需要多次递归,才能找到 1 的下标0)
使用插值查找算法:
m i d = l e f t + ( r i g h t – l e f t ) f i n d V a l – a r r [ l e f t ] a r r [ r i g h t ] – a r r [ l e f t ] \begin{aligned}&mid = left + (right – left)\frac{findVal – arr[left]}{arr[right] – arr[left]}\end{aligned} mid=left+(right–left)arr[right]–arr[left]findVal–arr[left]
即:
m i d = 0 + ( 99 − 0 ) 1 − 1 100 − 1 = 0 + 99 ∗ 0 99 = 0 ( 直接定位到下标 0 ) \begin{aligned}&mid = 0+(99-0)\frac{1-1}{100-1} = 0 + 99 * \frac{0}{99} = 0\ \ \ (直接定位到下标0)\end{aligned} mid=0+(99−0)100−11−1=0+99∗990=0 (直接定位到下标0)
②假如需要查找的值是 100
m i d = 0 + ( 99 − 0 ) 100 − 1 ( 100 − 1 = 0 + 99 ∗ 99 99 = 0 + 99 = 99 ( 直接定位到下标 99 ) \begin{aligned}&mid =0 + (99 - 0)\frac{100 - 1}{(100 - 1} = 0 + 99 * \frac{99}{99} = 0 + 99 = 99\ \ \ (直接定位到下标99)\end{aligned} mid=0+(99−0)(100−1100−1=0+99∗9999=0+99=99 (直接定位到下标99)
3.3. 实例应用
问题:
对数组 arr = [1, 2, 3, …, 100] ,使用插值查找算法,找到 1 的索引值(下标)
代码实现:
package search;import java.util.Arrays;public class InsertValueSearch {public static void main(String[] args) {int[] arr = new int[100];for (int i = 0; i < 100; i++) {arr[i] = i + 1;}int index = insertValueSearch(arr, 0, arr.length - 1, 1);System.out.println("index = " + index);// System.out.println(Arrays.toString(arr));}// 编写插值查找算法// 说明:插值查找算法也要求数组是有序的/*** * @param arr 数组* @param left 左边索引* @param right 右边索引* @param findVal 要查找的值* @return 如果找到,就返回对应的下标;如果没有找到,就返回-1*/public static int insertValueSearch(int[] arr, int left, int right, int findVal) {System.out.println("查找了一次");// 注意:findVal < arr[0] 和 findVal > arr[arr.length - 1] 必须需要,否则得到的mid可能越界if (left > right || findVal < arr[0] || findVal > arr[arr.length - 1]) {return -1;}// 求出 midint mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left]);int midVal = arr[mid];if (findVal > midVal) {// 说明应该向右边递归return insertValueSearch(arr, mid + 1, right, findVal);} else if (findVal < midVal) {// 说明应该向左递归return insertValueSearch(arr, left, mid - 1, findVal);} else {return mid;}}}
运行结果:
注意事项:
- 对于数据量较大,关键字分布比较均匀的查找表来说,采用插值查找, 速度较快.
- 关键字分布不均匀的情况下,该方法不一定比折半(二分)查找要好
4. 斐波那契(黄金分割法)查找算法
黄金分割点是指把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比。取其前三位数字的近似值是 0.618。由于按此比例设计的造型十分美丽,因此称为黄金分割,也称为中外比。这是一个神奇的数字,会带来意想不到的效果。
斐波那契数列 {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … … } 发现斐波那契数列的两个相邻数 的比例,无限接近 黄金分割值0.618。
4.1. 斐波那契(黄金分割法)原理
斐波那契查找原理与前两种相似,仅仅改变了中间结点(mid)的位置,mid 不再是中间或插值得到,而是位于黄金分割点附近,即 m i d = l o w + F [ k − 1 ] − 1 mid=low+F[k-1]-1 mid=low+F[k−1]−1( F F F 代表斐波那契数列),如下图所示:

对 F(k-1)-1 的理解:
- 由斐波那契数列 F [ k ] = F [ k − 1 ] + F [ k − 2 ] F[k]=F[k-1]+F[k-2] F[k]=F[k−1]+F[k−2] 的性质,可以得到 ( F [ k ] − 1 ) = ( F [ k − 1 ] − 1 ) + ( F [ k − 2 ] − 1 ) + 1 (F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1 (F[k]−1)=(F[k−1]−1)+(F[k−2]−1)+1 。该式说明:只要顺序表的长度为 F[k]-1,则可以将该表分成长度为 F [ k − 1 ] − 1 F[k-1]-1 F[k−1]−1 和 F [ k − 2 ] − 1 F[k-2]-1 F[k−2]−1 的两段,即如上图所示。从而中间位置为 m i d = l o w + F [ k − 1 ] − 1 mid=low+F[k-1]-1 mid=low+F[k−1]−1
- 类似的,每一子段也可以用相同的方式分割
- 但顺序表长度 n n n 不一定刚好等于 F [ k ] − 1 F[k]-1 F[k]−1,所以需要将原来的顺序表长度 n n n 增加至 F [ k ] − 1 F[k]-1 F[k]−1。这里的 k k k 值只要能使得 F [ k ] − 1 F[k]-1 F[k]−1 恰好大于或等于 n n n 即可,由以下代码得到,顺序表长度增加后,新增的位置(从 n + 1 n+1 n+1 到 F [ k ] − 1 F[k]-1 F[k]−1 位置),都赋为 n n n 位置的值即可。
while(n>fib(k)-1)
k++;
4.2. 实例应用
问题:
请对一个有序数组进行斐波那契查找 {1,8, 10, 89, 1000, 1234} ,输入一个数看看该数组是否存在此数,并且求出下标,如果没有就提示"没有这个数"(return = -1)。
代码实现:
package search;import java.util.Arrays;public class FibonacciSearch {public static int maxSize = 20;public static void main(String[] args) {int[] arr = { 1, 8, 10, 89, 1000, 1234 };System.out.println("index = " + fibSearch(arr, 89));}// 因为后面我们mid=low+F(k-1)-1,需要使用斐波那契数列,因此我们需要先获取到一个斐波那契数列// 非递归方法得到一个斐波那契数列public static int[] fib() {int[] f = new int[maxSize];f[0] = 1;f[1] = 1;for (int i = 2; i < maxSize; i++) {f[i] = f[i - 1] + f[i - 2];}return f;}// 编写斐波那契查找算法// 使用非递归的方式编写算法/*** * @param a 数组* @param key 需要查找的关键字(值)* @return 返回对应的下标,如果没有,就返回-1*/public static int fibSearch(int[] a, int key) {int low = 0;int high = a.length - 1;int k = 0;// 表示斐波那契分割数值的下标int mid = 0;// 存放mid值int f[] = fib();// 获取到斐波那契数列// 获取到斐波那契分割数值的下标while (high > f[k] - 1) {k++;}// 因为f[k]的值 可能大于a的长度,因此需要使用Arrays类,构造一个新的数组,并指向a[]// 不足的部分会使用0填充int[] temp = Arrays.copyOf(a, f[k]);// 实际上,需要使用a数组的最后的数填充temp// 举例:// temp = {1,8,10,89,1000,1234,0,0,0} --> {1,8,10,89,1000,1234,1234,1234,1234}for (int i = high + 1; i < temp.length; i++) {temp[i] = a[high];}// 使用while循环处理,找到keywhile (low <= high) {// 只要这个条件满足,就可以找mid = low + f[k - 1] - 1;if (key < temp[mid]) {// 继续向数组的前面查找(左边)high = mid - 1;// 为什么是k--?// 说明:// 1. 全部元素=前面的元素+后面的元素// 2. f[k] = f[k-1] + f[k-2]// 因为 前面有f[k-1]个元素,所以可以继续拆分 f[k-1] = f[k-2] + f[k-3]// 即 在f[k-1]的前面继续查找(k--)// 即 下次循环的 mid = f[k-1-1]-1k--;} else if (key > temp[mid]) {// 继续向数组的后面查找(右边)low = mid + 1;// 为什么是 k -= 2// 说明// 1. 全部元素=前面的元素+后面的元素// 2. f[k] = f[k-1] + f[k-2]// 因为 后面有f[k-2]个元素,所以可以继续拆分 f[k-2] = f[k-3] + f[k-4]// 即 在f[k-2]的后面继续查找(k-=2)// 即 下次循环的 mid = f[k-1-2]-1k -= 2;} else {// 找到// 需要确定,返回的是哪一个下标if (mid <= high) {return mid;} else {return high;}}}return -1;}}
运行结果:
相关文章:
【数据结构(七)】查找算法
文章目录 查找算法介绍1. 线性查找算法2. 二分查找算法2.1. 思路分析2.2. 代码实现2.3. 功能拓展 3. 插值查找算法3.1. 前言3.2. 相关概念3.3. 实例应用 4. 斐波那契(黄金分割法)查找算法4.1. 斐波那契(黄金分割法)原理4.2. 实例应用 查找算法介绍 在 java 中,我们…...
Android画布Canvas绘制drawBitmap基于源Rect和目的Rect,Kotlin
Android画布Canvas绘制drawBitmap基于源Rect和目的Rect,Kotlin <?xml version"1.0" encoding"utf-8"?> <androidx.appcompat.widget.LinearLayoutCompat xmlns:android"http://schemas.android.com/apk/res/android"xmlns…...
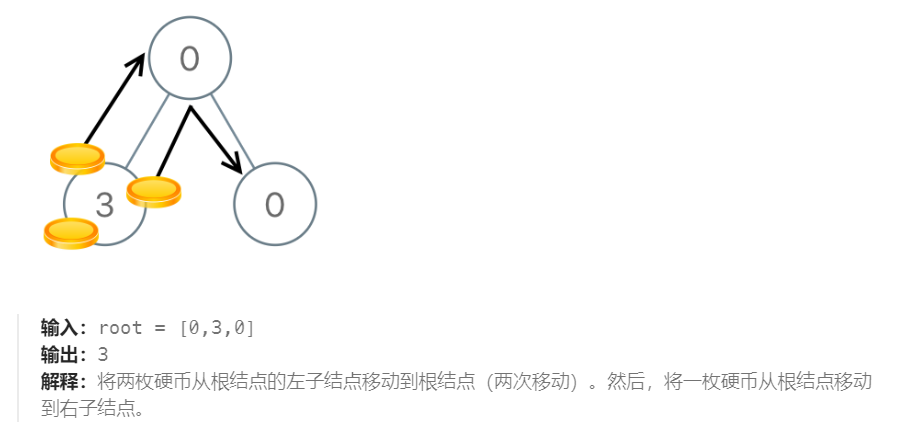
深度优先搜索LeetCode979. 在二叉树中分配硬币
给你一个有 n 个结点的二叉树的根结点 root ,其中树中每个结点 node 都对应有 node.val 枚硬币。整棵树上一共有 n 枚硬币。 在一次移动中,我们可以选择两个相邻的结点,然后将一枚硬币从其中一个结点移动到另一个结点。移动可以是从父结点到…...
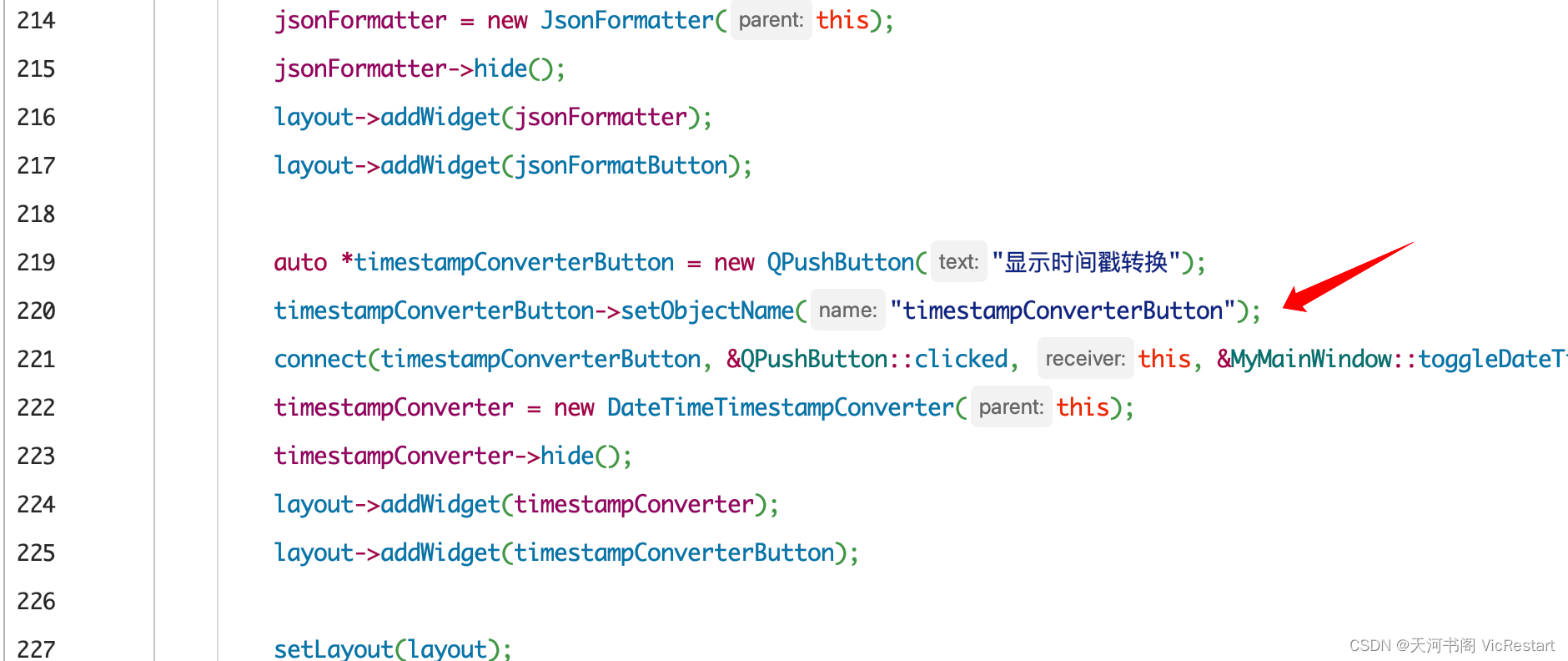
C++学习之路(十)C++ 用Qt5实现一个工具箱(增加一个时间戳转换功能)- 示例代码拆分讲解
上篇文章,我们用 Qt5 实现了在小工具箱中添加了《JSON数据格式化》功能,还是比较实用的。为了继续丰富我们的工具箱,今天我们就再增加一个平时经常用到的功能吧,就是「 时间戳转换 」功能,而且实现点击按钮后文字进行变…...

Linux 5.15安全特性之ARM64 PAC
ARM64 PAC(Pointer Authentication Code)机制是ARM架构中引入的一种安全特性,旨在提供指针的完整性和安全性保护。它通过在指针中插入一段额外的代码进行签名,以验证指针的完整性,从而抵御缓冲区溢出和代码注入等攻击。…...

同旺科技 分布式数字温度传感器
内附链接 1、数字温度传感器 主要特性有: ● 支持PT100 / PT1000 两种铂电阻; ● 支持 2线 / 3线 / 4线 制接线方式; ● 支持5V~17V DC电源供电; ● 支持电源反接保护; ● 支持通讯波特率1200bps、2…...

状态空间的定义
状态空间是描述一个系统所有可能状态的集合。在系统理论、控制论、计算机科学、强化学习等领域,状态空间是一种常见的概念。 状态空间框架是一种用于描述和分析系统的方法,它包括系统的状态、状态之间的转移关系以及与状态相关的行为。下面详细解释状态…...

数据挖掘实战-基于word2vec的短文本情感分析
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...

大数据面试总结
1、冒泡排序、选择排序 2、二分查找 3、 hashmap和hashtable的区别?hashmap的底层实现原理? a、hashtable和hashmap的区别: 1、hashtable是线程安全的,会在每一个方法中都添加方法synchronize(同步机制)…...
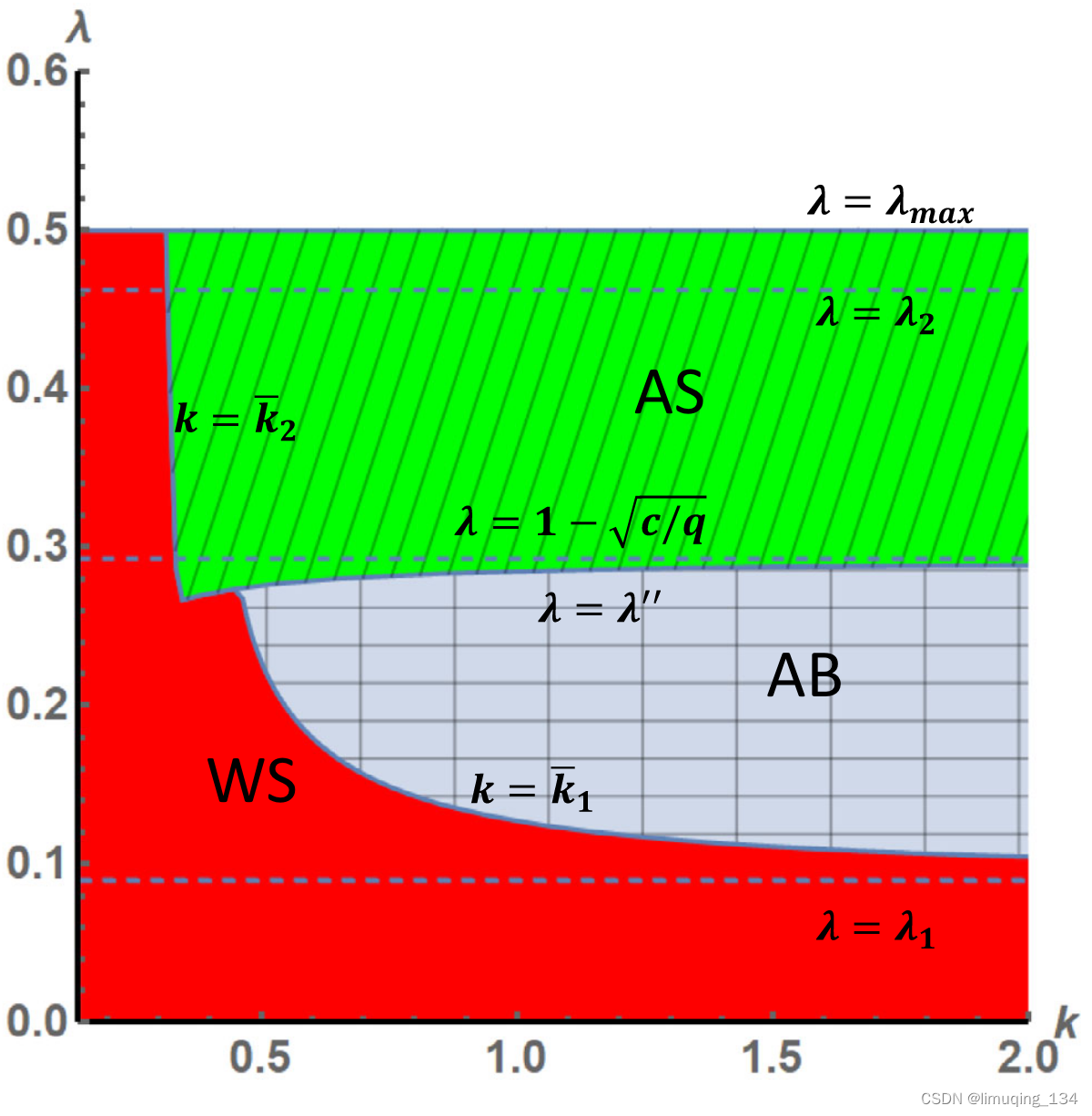
利大于弊:物联网技术对电子商务渠道的影响
For Better or For Worse: Impacts of IoT Technology in e-Commerce Channel 物联网技术使用传感器和其他联网设备来手机和共享数据,并且被视为一种可以为供应链成员带来巨大的机会的突破性技术。本文的研究背景是:一个提供物联网基础设备的电子商务平…...
)
Python 元组详解(tuple)
文章目录 1 概述1.1 性质1.2 下标1.3 切片 2 常用方法2.1 访问:迭代、根据下标2.2 删除:del2.3 运算符:、*2.4 计算元组中元素个数:len()2.5 返回元组中元素最大值:max()2.6 返回元组中元素最小值:min()2.7…...

Redis部署-主从模式
目录 单点问题 主从模式 解析主从模式 配置redis主从模式 info replication命令查看复制相关的状态 断开复制关系 安全性 只读 传输延迟 拓扑结构 数据同步psync replicationid offset psync运行流程 全量复制流程 无硬盘模式 部分复制流程 积压缓冲区 实时复…...

全栈冲刺 之 一天速成MySQL
一、为什么使用数据库 数据储存在哪里? 硬盘、网盘、U盘、光盘、内存(临时存储) 数据持久化 使用文件来进行存储,数据库也是一种文件,像excel ,xml 这些都可以进行数据的存储,但大量数据操作…...

服务器运行train.py报错解决
在服务器配置完虚拟环境以及安装完各种所需库后,发现报错Traceback (most recent call last): File "/root/yolov5-master/yolov5-master/train.py", line 48, in <module> import val as validate # for end-of-epoch mAP File "/root/yolov5…...

Flutter开发type ‘Future<int>‘ is not a subtype of type ‘int‘ in type cast错误
文章目录 问题描述错误源码 问题分析解决方法修改后的代码 问题描述 今天有个同事调试flutter程序时报错,问我怎么解决,程序运行时报如下错误: type ‘Future’ is not a subtype of type ‘int’ in type cast 错误源码 int order Databas…...
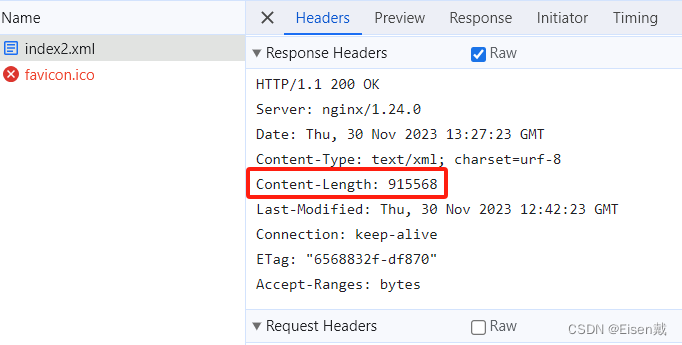
Nginx(十二) gzip gzip_static sendfile directio aio 组合使用测试(2)
测试10:开启gzip、sendfile、aio、directio1m,关闭gzip_static,请求/index.js {"time_iso8601":"2023-11-30T17:20:5508:00","request_uri":"/index.js","status":"200","…...

hls实现播放m3u8视频将视频流进行切片 HLS.js简介
github官网GitHub - video-dev/hls.js: HLS.js is a JavaScript library that plays HLS in browsers with support for MSE.HLS.js is a JavaScript library that plays HLS in browsers with support for MSE. - GitHub - video-dev/hls.js: HLS.js is a JavaScript library …...
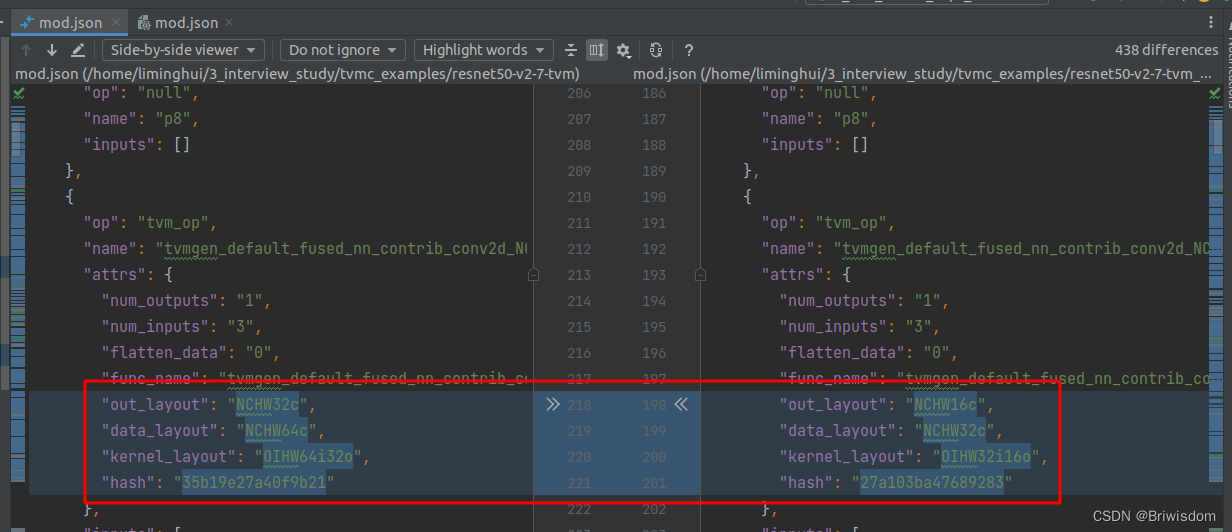
Ubuntu20.04部署TVM流程及编译优化模型示例
前言:记录自己安装TVM的流程,以及一个简单的利用TVM编译模型并执行的示例。 1,官网下载TVM源码 git clone --recursive https://github.com/apache/tvmgit submodule init git submodule update顺便完成准备工作,比如升级cmake版本…...
)
华为OD机试真题-两个字符串间的最短路径问题-2023年OD统一考试(C卷)
题目描述: 给定两个字符串,分别为字符串A与字符串B。例如A字符串为ABCABBA,B字符串为CBABAC可以得到下图m*n的二维数组,定义原点为(0, 0),终点为(m, n),水平与垂直的每一条边距离为1,映射成坐标系如下图。 从原点(0, 0)到(0, A)为水平边,距离为1,从(0, A)到(A, C)为垂…...

python try-except
相比于直接raise ValueError,使用try-except可以使程序在发生异常后仍然能够运行。 在try的部分中,当遇到第一个Error,就跳转到except中寻找对应类型的error,后续代码不再执行,如果try中有多个Error,注意顺…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
