MIT线性代数笔记-第23讲-微分方程,exp(At)
目录
- 23.微分方程, e x p ( A t ) exp(At) exp(At)
- 用矩阵求解微分方程
- 矩阵指数
- 二阶常微分方程
- 打赏
23.微分方程, e x p ( A t ) exp(At) exp(At)
用矩阵求解微分方程
例: { d u 1 d t = − u 1 + 2 u 2 d u 2 d t = u 1 − 2 u 2 \left \{ \begin{matrix} \dfrac{du_1}{dt} = -u_1 + 2u_2 \\ \dfrac{du_2}{dt} = u_1 - 2u_2 \end{matrix} \right. ⎩ ⎨ ⎧dtdu1=−u1+2u2dtdu2=u1−2u2,其中 u 1 , u 2 u_1 , u_2 u1,u2是 t t t的两个不同函数且 u 1 ( 0 ) = 1 , u 2 ( 0 ) = 0 u_1(0) = 1 , u_2(0) = 0 u1(0)=1,u2(0)=0
令 A = [ − 1 2 1 − 2 ] , u ⃗ = [ u 1 u 2 ] A = \begin{bmatrix} -1 & 2 \\ 1 &-2 \end{bmatrix} , \vec{u} = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} A=[−112−2],u=[u1u2],则有 d u ⃗ d t = A u ⃗ , u ⃗ ( 0 ) = [ 1 0 ] \dfrac{d \vec{u}}{dt} = A \vec{u} , \vec{u}(0) = \begin{bmatrix} 1 \\ 0 \end{bmatrix} dtdu=Au,u(0)=[10]
先求 A A A的特征向量和特征值,因为 A A A已经是一个奇异矩阵,所以 A A A有一个特征值为 λ 1 = 0 \lambda_1 = 0 λ1=0,又主对角线元素和为 − 3 -3 −3,所以另一个特征值为 λ 2 = − 3 \lambda_2 = -3 λ2=−3,两个特征值分别对应特征向量 x 1 ⃗ = [ 2 1 ] , x 2 ⃗ = [ 1 − 1 ] \vec{x_1} = \begin{bmatrix} 2 \\ 1 \end{bmatrix} , \vec{x_2} = \begin{bmatrix} 1 \\ -1 \end{bmatrix} x1=[21],x2=[1−1]
求出特征值和特征向量后便可以得到方程的两个特解 e λ 1 t x 1 ⃗ , e λ 2 t x 2 ⃗ e^{\lambda_1 t} \vec{x_1} , e^{\lambda_2 t} \vec{x_2} eλ1tx1,eλ2tx2,可以验证一下
将 u ⃗ = e λ 1 t x 1 ⃗ \vec{u} = e^{\lambda_1 t} \vec{x_1} u=eλ1tx1代入得: d u ⃗ d t = d e λ 1 t x 1 ⃗ d t = λ 1 e λ 1 t x 1 ⃗ = e λ 1 t λ 1 x 1 ⃗ = e λ 1 t A x 1 ⃗ = A e λ 1 t x 1 ⃗ \dfrac{d \vec{u}}{dt} = \dfrac{de^{\lambda_1 t} \vec{x_1}}{dt} = \lambda_1 e^{\lambda_1 t} \vec{x_1} = e^{\lambda_1 t} \lambda_1 \vec{x_1} = e^{\lambda_1 t} A \vec{x_1} = A e^{\lambda_1 t} \vec{x_1} dtdu=dtdeλ1tx1=λ1eλ1tx1=eλ1tλ1x1=eλ1tAx1=Aeλ1tx1, e λ 2 t x 2 ⃗ e^{\lambda_2 t} \vec{x_2} eλ2tx2同理
但是这两个特解仅仅满足了方程成立,并不一定满足 u ⃗ ( 0 ) = [ 1 0 ] \vec{u}(0) = \begin{bmatrix} 1 \\ 0 \end{bmatrix} u(0)=[10],不过容易证得这两个特解的任意线性组合也是方程的解,而且这两个特解线性无关,无论给出的 u ⃗ ( t 0 ) \vec{u}(t_0) u(t0)是什么均可以表示
所以设 u ⃗ = c 1 e λ 1 t x 1 ⃗ + c 2 e λ 2 t x 2 ⃗ \vec{u} = c_1 e^{\lambda_1 t} \vec{x_1} + c_2 e^{\lambda_2 t} \vec{x_2} u=c1eλ1tx1+c2eλ2tx2,将 u ⃗ ( 0 ) = [ 1 0 ] \vec{u}(0) = \begin{bmatrix} 1 \\ 0 \end{bmatrix} u(0)=[10]代入得: [ 1 0 ] = c 1 e 0 [ 2 1 ] + c 2 e 0 [ 1 − 1 ] \begin{bmatrix} 1 \\ 0 \end{bmatrix} = c_1 e^{0} \begin{bmatrix} 2 \\ 1 \end{bmatrix} + c_2 e^{0} \begin{bmatrix} 1 \\ -1 \end{bmatrix} [10]=c1e0[21]+c2e0[1−1],解得: c 1 = c 2 = 1 3 c_1 = c_2 = \dfrac{1}{3} c1=c2=31
因而 u ⃗ = 1 3 [ 2 1 ] + 1 3 e − 3 t [ 1 − 1 ] \vec{u} = \dfrac{1}{3} \begin{bmatrix} 2 \\ 1 \end{bmatrix} + \dfrac{1}{3} e^{-3t} \begin{bmatrix} 1 \\ -1 \end{bmatrix} u=31[21]+31e−3t[1−1]
将 u 1 , u 2 u_1 , u_2 u1,u2视作两个容器,将 t t t视作时间,由 u ⃗ ( 0 ) = [ 1 0 ] \vec{u}(0) = \begin{bmatrix} 1 \\ 0 \end{bmatrix} u(0)=[10]可知刚开始 u 1 u_1 u1中有 1 1 1的货物, u 2 u_2 u2中没有货物,但是随着 t t t的增大,即时间的流逝,由于 u 1 ′ < 0 , u 2 ′ > 0 u_1^{'} < 0 , u_2^{'} > 0 u1′<0,u2′>0, u 1 u_1 u1中的货物渐渐流向了 u 2 u_2 u2
可以发现当 t → + ∞ t \to +\infty t→+∞时, e − 3 t → 0 e^{-3t} \to 0 e−3t→0,所以 u ⃗ → 1 3 [ 2 1 ] \vec{u} \to \dfrac{1}{3} \begin{bmatrix} 2 \\ 1 \end{bmatrix} u→31[21],即 u ⃗ \vec{u} u收敛于 1 3 [ 2 1 ] \dfrac{1}{3} \begin{bmatrix} 2 \\ 1 \end{bmatrix} 31[21],此时称 1 3 [ 2 1 ] \dfrac{1}{3} \begin{bmatrix} 2 \\ 1 \end{bmatrix} 31[21]为 u ⃗ \vec{u} u的稳态
证明稳态存在的条件为所有特征值的实部均为非负数:
若特征值为实数, lim t → + ∞ e a t = { 1 , a = 0 0 , a < 0 \lim_{t \to +\infty} e^{at} = \left \{ \begin{matrix} 1 , a = 0 \\ 0 , a < 0 \end{matrix} \right. limt→+∞eat={1,a=00,a<0
若特征值为复数, e ( a + b i ) t = e a t ⋅ e b t i = e a t ( c o s b t + i s i n b t ) e^{(a + bi)t} = e^{at} \cdot e^{bti} = e^{at} (cos\ bt + i\ sin\ bt) e(a+bi)t=eat⋅ebti=eat(cos bt+i sin bt),想要当 t → + ∞ t \to +\infty t→+∞时该项对 u ⃗ \vec{u} u的影响不会无限增大,就要让 ∣ e a t ( c o s b t + i s i n b t ) ∣ |e^{at} (cos\ bt + i\ sin\ bt)| ∣eat(cos bt+i sin bt)∣趋于稳定,而 ∣ c o s b t + i s i n b t ∣ = 1 |cos\ bt + i\ sin\ bt| = 1 ∣cos bt+i sin bt∣=1,所以只要让 e a t e^{at} eat趋于稳定,那么又回到了特征值为实数的情况,所以 a ≤ 0 a \le 0 a≤0即可
综上, R e λ ≤ 0 Re\ \lambda \le 0 Re λ≤0即可
-
容易证得所有特征值的实部均为负数时,稳态为 0 ⃗ \vec{0} 0
-
考虑 A A A为二阶方阵时,满足什么 u ⃗ \vec{u} u才能有稳态,设 A = [ a b c d ] A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} A=[acbd],其实不用求出特征值就可以判断
若特征值均为复数,因为 a + d = λ 1 + λ 2 a + d = \lambda_1 + \lambda_2 a+d=λ1+λ2且 λ 1 , λ 2 \lambda_1 , \lambda_2 λ1,λ2为共轭复数,所以只需满足 a + d ≤ 0 a + d \le 0 a+d≤0即可
若特征值均为实数,此时 { λ 1 + λ 2 ≤ 0 λ 1 ⋅ λ 2 ≥ 0 \left \{ \begin{matrix} \lambda_1 + \lambda_2 \le 0 \\ \lambda_1 \cdot \lambda_2 \ge 0 \end{matrix} \right. {λ1+λ2≤0λ1⋅λ2≥0与稳态存在的条件等价,而 a + d = λ 1 + λ 2 , ∣ A ∣ = λ 1 ⋅ λ 2 a + d = \lambda_1 + \lambda_2 , |A| = \lambda_1 \cdot \lambda_2 a+d=λ1+λ2,∣A∣=λ1⋅λ2,所以只要满足 { a + d ≤ 0 ∣ A ∣ ≥ 0 \left \{ \begin{matrix} a + d \le 0 \\ |A| \ge 0 \end{matrix} \right. {a+d≤0∣A∣≥0即可
当特征值均为复数时,因为两个特征值为共轭复数,所以 ∣ A ∣ = λ 1 ⋅ λ 2 ≥ 0 |A| = \lambda_1 \cdot \lambda_2 \ge 0 ∣A∣=λ1⋅λ2≥0恒成立
综上只需满足 { a + d ≤ 0 ∣ A ∣ ≥ 0 \left \{ \begin{matrix} a + d \le 0 \\ |A| \ge 0 \end{matrix} \right. {a+d≤0∣A∣≥0即可
矩阵指数
A A A表示了 u ⃗ \vec{u} u各个元素之间的耦合方式,求 A A A的特征值和特征向量即为解耦,接下来换一种解耦思路
设 u ⃗ = S v ⃗ \vec{u} = S \vec{v} u=Sv,代入得: S d v ⃗ d t = A S v ⃗ S \dfrac{d \vec{v}}{dt} = AS \vec{v} Sdtdv=ASv,左右同时乘 S − 1 S^{-1} S−1得: d v ⃗ d t = S − 1 A S v ⃗ = Λ v ⃗ \dfrac{d \vec{v}}{dt} = S^{-1} AS \vec{v} = \Lambda \vec{v} dtdv=S−1ASv=Λv
这样就转化为了关于 v ⃗ \vec{v} v的方程,又因为 Λ \Lambda Λ为对角阵,所以 v ⃗ \vec{v} v各个元素之间不存在耦合,因而 v n = c n ⋅ e λ n t v_n = c_n \cdot e^{\lambda_n t} vn=cn⋅eλnt,将 v n ( 0 ) v_n(0) vn(0)代入得: v n = v n ( 0 ) ⋅ e λ n t v_n = v_n(0) \cdot e^{\lambda_n t} vn=vn(0)⋅eλnt,所以 v ⃗ = e Λ t v ⃗ ( 0 ) \vec{v} = e^{\Lambda t} \vec{v}(0) v=eΛtv(0),所以 u ⃗ = S v ⃗ = S e Λ t v ⃗ ( 0 ) = S e Λ t S − 1 u ⃗ ( 0 ) = e A t u ⃗ ( 0 ) \vec{u} = S \vec{v} = S e^{\Lambda t} \vec{v}(0) = S e^{\Lambda t} S^{-1} \vec{u}(0) = e^{At} \vec{u}(0) u=Sv=SeΛtv(0)=SeΛtS−1u(0)=eAtu(0),是不是看不懂?没关系,现在就来解释
引入矩阵指数,即底数为 e e e,指数为矩阵
e x e^x ex的麦克劳林公式为 e x = 1 + x + x 2 2 ! + x 3 3 ! + ⋯ + x n n ! + ⋯ e^x = 1 + x + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \cdots + \dfrac{x^n}{n!} + \cdots ex=1+x+2!x2+3!x3+⋯+n!xn+⋯
指数为矩阵时也一样,即 e x = I + A + A 2 2 ! + A 3 3 ! + ⋯ + A n n ! + ⋯ e^x = I + A + \dfrac{A^2}{2!} + \dfrac{A^3}{3!} + \cdots + \dfrac{A^n}{n!} + \cdots ex=I+A+2!A2+3!A3+⋯+n!An+⋯
拓展: 这用到了一个经典的麦克劳林级数 e x = ∑ 0 + ∞ x n n ! e^x = \sum_{0}^{+\infty} \dfrac{x^n}{n!} ex=∑0+∞n!xn,其实另一个经典的麦克劳林级数 1 1 − x = ∑ 0 + ∞ x n \dfrac{1}{1 - x} = \sum_{0}^{+\infty} x^n 1−x1=∑0+∞xn也对矩阵适用,即 ( I − A ) − 1 = I + A + A 2 + ⋯ + A n + ⋯ (I - A)^{-1} = I + A + A^2 + \cdots + A^n + \cdots (I−A)−1=I+A+A2+⋯+An+⋯,当 A A A的所有特征值的绝对值都小于 1 1 1(如果特征值为复数,则模小于 1 1 1)时,这可以很方便的用来求矩阵的逆的近似值
证明当 A A A为对角阵时 e i , i A = e a i , i : e^A_{i , i} = e^{a_{i , i}}: ei,iA=eai,i:
对于对角阵有 A i , i k = a i , i k A^k_{i , i} = a_{i , i}^k Ai,ik=ai,ik,所以在用 A A A代入麦克劳林公式时, A A A的主对角线上的元素都分别代入了一次麦克劳林公 式,那么自然会变为 e e e的幂
所以 v ⃗ = [ e λ 1 t 0 ⋯ 0 0 e λ 2 t ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ e λ n t ] v ⃗ ( 0 ) = e Λ t v ⃗ ( 0 ) \vec{v} = \begin{bmatrix} e^{\lambda_1 t} & 0 & \cdots & 0 \\ 0 & e^{\lambda_2 t} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & e^{\lambda_n t} \end{bmatrix} \vec{v}(0)= e^{\Lambda t} \vec{v}(0) v= eλ1t0⋮00eλ2t⋮0⋯⋯⋱⋯00⋮eλnt v(0)=eΛtv(0)
证明 e A t = S e Λ t S − 1 e^{At} = S e^{\Lambda t} S^{-1} eAt=SeΛtS−1:
e A t = I + A t + ( A t ) 2 2 ! + ( A t ) 3 3 ! + ⋯ + ( A t ) n n ! + ⋯ = I + S Λ S − 1 t + S Λ 2 S − 1 t 2 2 ! + ⋯ + S Λ n S − 1 t n n ! + ⋯ = S [ I + Λ t + ( Λ t ) 2 2 ! + ⋯ + ( Λ t ) n n ! + ⋯ ] S − 1 = S e Λ t S − 1 \begin{aligned} e^{At} & = I + At + \dfrac{(At)^2}{2!} + \dfrac{(At)^3}{3!} + \cdots + \dfrac{(At)^n}{n!} + \cdots \\ & = I + S \Lambda S^{-1} t + \dfrac{S \Lambda^2 S^{-1} t^2}{2!} + \cdots + \dfrac{S \Lambda^n S^{-1} t^n}{n!} + \cdots \\ & = S [I + \Lambda t + \dfrac{(\Lambda t)^2}{2!} + \cdots + \dfrac{(\Lambda t)^n}{n!} + \cdots] S^{-1} \\ & = S e^{\Lambda t} S^{-1} \end{aligned} eAt=I+At+2!(At)2+3!(At)3+⋯+n!(At)n+⋯=I+SΛS−1t+2!SΛ2S−1t2+⋯+n!SΛnS−1tn+⋯=S[I+Λt+2!(Λt)2+⋯+n!(Λt)n+⋯]S−1=SeΛtS−1
想要让 e A t → O e^{At} \to O eAt→O,那么就需要 e Λ t → O e^{\Lambda t} \to O eΛt→O,即 e λ t → 0 e^{\lambda t} \to 0 eλt→0,即 R e λ < 0 Re\ \lambda < 0 Re λ<0
二阶常微分方程
对于一个二阶常微分方程 y ′ ′ + b y ′ + k y = 0 y^{''} + b y^{'} + ky = 0 y′′+by′+ky=0,令 u ⃗ = [ y ′ y ] \vec{u} = \begin{bmatrix} y^{'} \\ y \end{bmatrix} u=[y′y],则 u ⃗ ′ = [ y ′ ′ y ′ ] \vec{u}^{'} = \begin{bmatrix} y^{''} \\ y^{'} \end{bmatrix} u′=[y′′y′]
所以 u ⃗ ′ = [ − b − k 1 0 ] u ⃗ \vec{u}^{'} = \begin{bmatrix} -b & -k \\ 1 & 0 \end{bmatrix} \vec{u} u′=[−b1−k0]u,设 A = [ − b − k 1 0 ] A = \begin{bmatrix} -b & -k \\ 1 & 0 \end{bmatrix} A=[−b1−k0],这样又可以利用矩阵求解
对于更高阶的微分方程也可以使用类似的方法
那样 u ⃗ , u ⃗ ′ \vec{u} , \vec{u}^{'} u,u′为 n n n阶向量, A A A为 n n n阶方阵且 A = [ _ _ ⋯ _ _ 1 0 ⋯ 0 0 0 1 ⋯ 0 0 ⋮ ⋮ ⋱ ⋮ ⋮ 0 0 ⋯ 1 0 ] A = \begin{bmatrix} \_ & \_ & \cdots & \_ & \_ \\ 1 & 0 & \cdots & 0 & 0\\ 0 & 1 & \cdots & 0 & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & 0\end{bmatrix} A= _10⋮0_01⋮0⋯⋯⋯⋱⋯_00⋮1_00⋮0 ,所以 0 0 0一定不是 A A A的特征值
最后还是要注意,本章所讲的内容仅对 A A A可对角化时有效,不是所有方阵都可以
打赏
制作不易,若有帮助,欢迎打赏!


相关文章:

MIT线性代数笔记-第23讲-微分方程,exp(At)
目录 23.微分方程, e x p ( A t ) exp(At) exp(At)用矩阵求解微分方程矩阵指数二阶常微分方程 打赏 23.微分方程, e x p ( A t ) exp(At) exp(At) 用矩阵求解微分方程 例: { d u 1 d t − u 1 2 u 2 d u 2 d t u 1 − 2 u 2 \left \{ \b…...
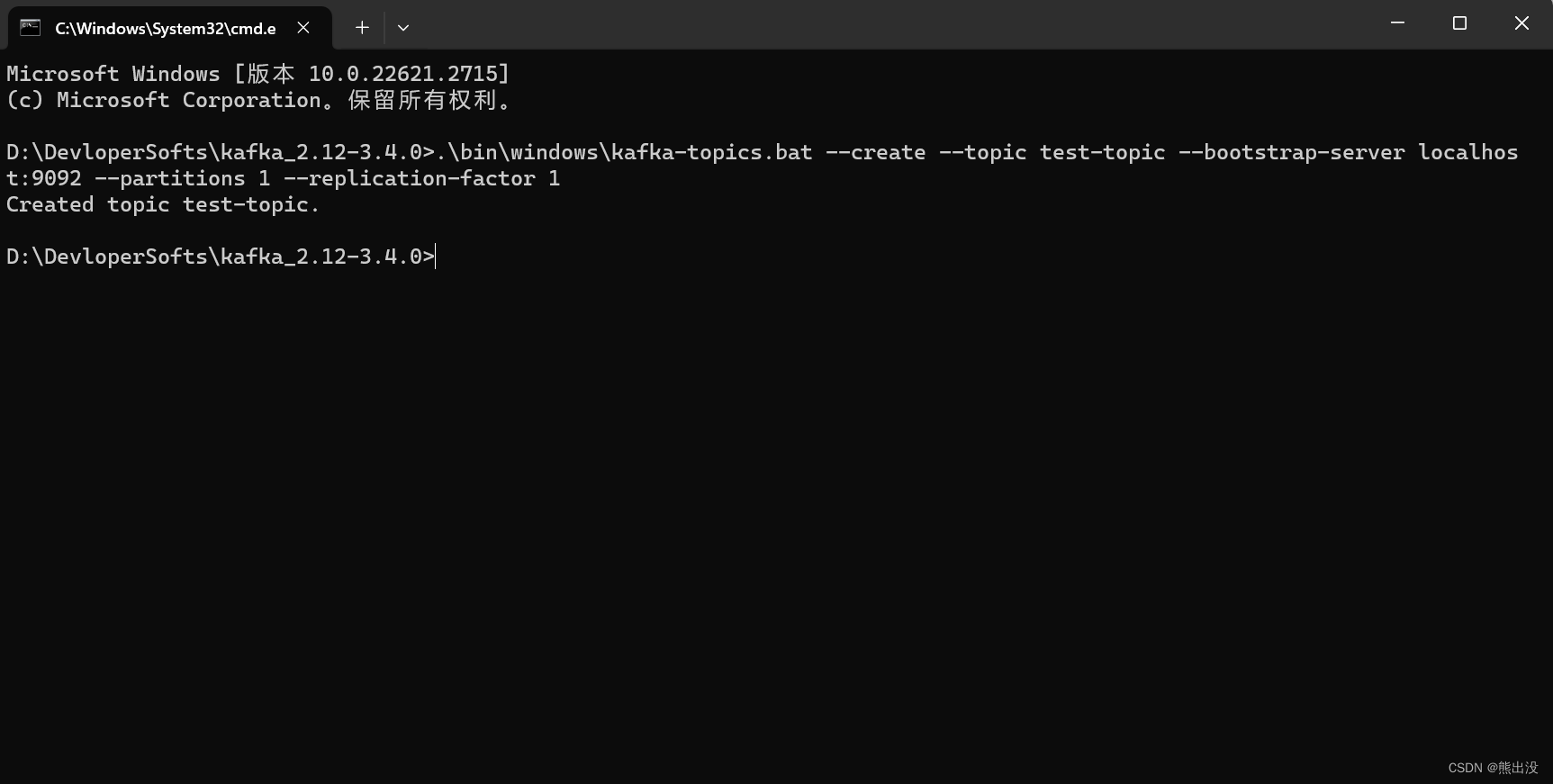
windows下安装配置kafka
一、安装zookeeper 在使用Kafka之前,通常需要先安装和配置ZooKeeper。ZooKeeper是Kafka的依赖项之一,它用于协调和管理Kafka集群的状态。 ZooKeeper是一个开源的分布式协调服务,它提供了可靠的数据存储和协调机制,用于协调分布式…...

TV遥控器模拟鼠标键
需求 : tv上部分app不支持光标选中,如亚马逊,插上鼠标不方便,即可以用遥控器模拟鼠标滚动和点击 1.拦截上下左右键 在WMS::PhoneWindowManager::interceptKeyBeforeQueueing中监听上下左右左右键,进行拦截。 Overrid…...
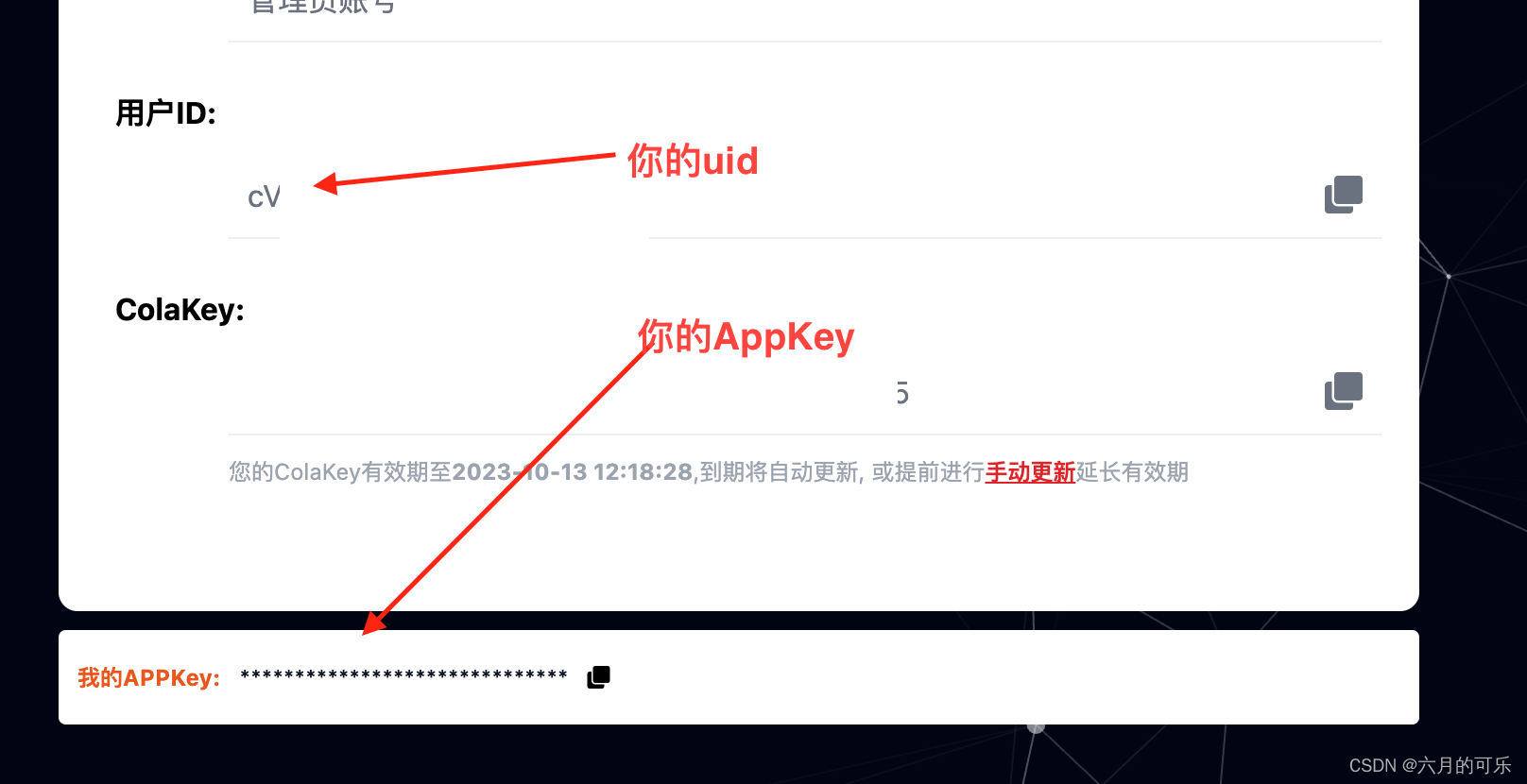
检测判断IP合法性API接口
检测判断IP合法性API接口 一、检测判断IP合法性API接口二、使用步骤1、接口2、请求参数3、请求参数示例4、接口 返回示例 三、 如何获取appKey和uid1、申请appKey:2、获取appKey和uid 四、重要说明 一、检测判断IP合法性API接口 一款免费的帮助你检测判断IP合法性API接口 二、…...
)
Linux swatch命令教程:如何监控系统活动(附案例详解和注意事项)
Linux swatch命令介绍 Swatch,全称为Simple Watcher,是一个简单的监视器,设计用于监控系统活动。为了使Swatch有用,它需要一个配置文件,该文件包含要查找的模式和在找到每个模式时要执行的操作。 Linux swatch命令适…...
训练的开源大型语言模型(LLM))
加州大学伯克利分校研究人员推出Starling-7B:一款通过人工智能反馈强化学习(RLAIF)训练的开源大型语言模型(LLM)
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
)
腾讯面试真题(C语言)
一.题目 求123...n,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。 二.题目剖析 首先题目要求不能用乘除,那么(首相末项)*项数/2就不能用,其次不…...

JavaScript 函数
JavaScript 函数 函数就是封装起来可以被重复使用的代码块 函数的优点 使代码更加简洁方便代码的修改和维护使程序运行更加高效 函数的封装(创建 声明)和调用 封装 通过function关键字封装 function 函数名(参数) {函数体:被封装的代码 }匿名函数 将一个函数直接赋值给一…...
数据结构 | 查漏补缺之DFS、BFS、二次探测再散列法、完全二叉树、深度计算
目录 DFS&BFS 哈希表-二次探测再散列法 完全二叉树&深度计算 排序 快速排序-挖坑法 插入、选择、冒泡、区别 DFS&BFS 哈希表-二次探测再散列法 完全二叉树&深度计算 排序 快速排序-挖坑法 插入、选择、冒泡、区别 插入从第一个元素开始,…...

用python实现单链表的基础操作
1 问题 用python实现单链表的基础操作:插入,删除,遍历,判空,清空链表,求长度,获取元素,判断元素是否存在。 2 方法 解决问题的步骤采用如下方式: 使用函数和类的方法来实…...
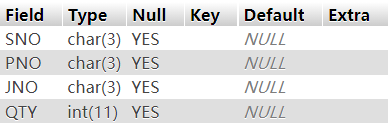
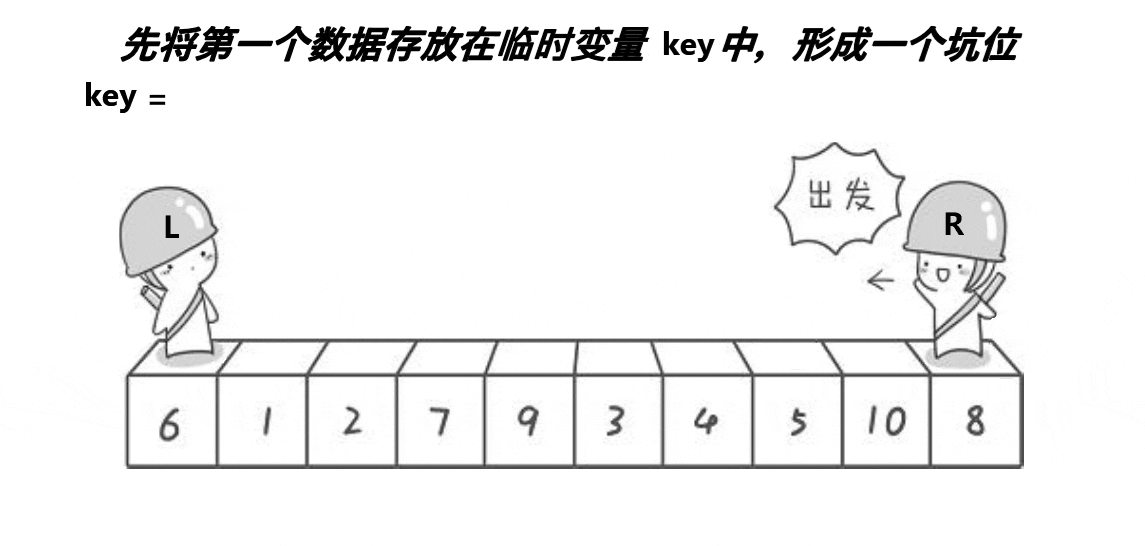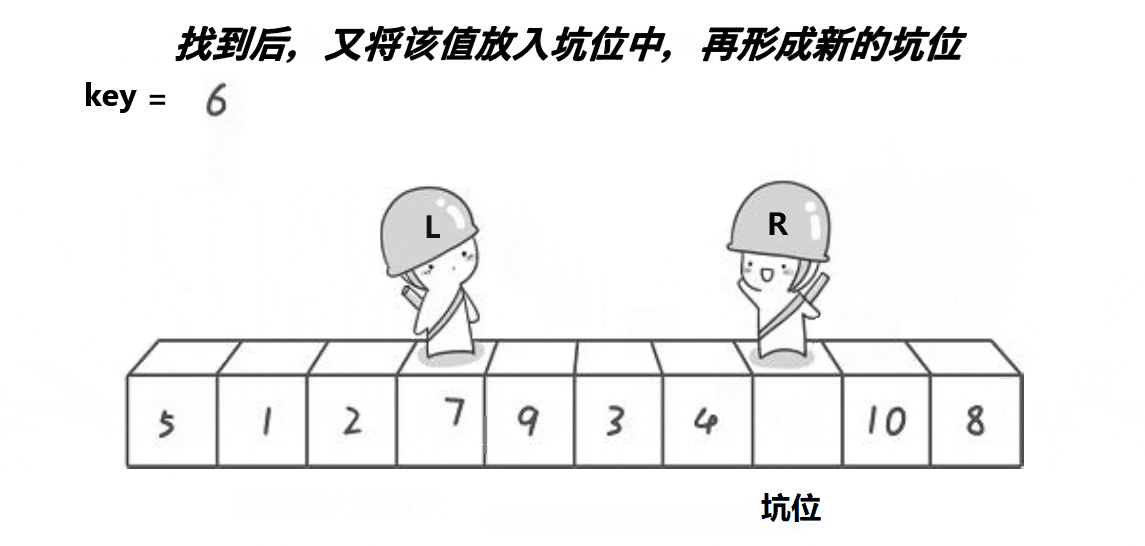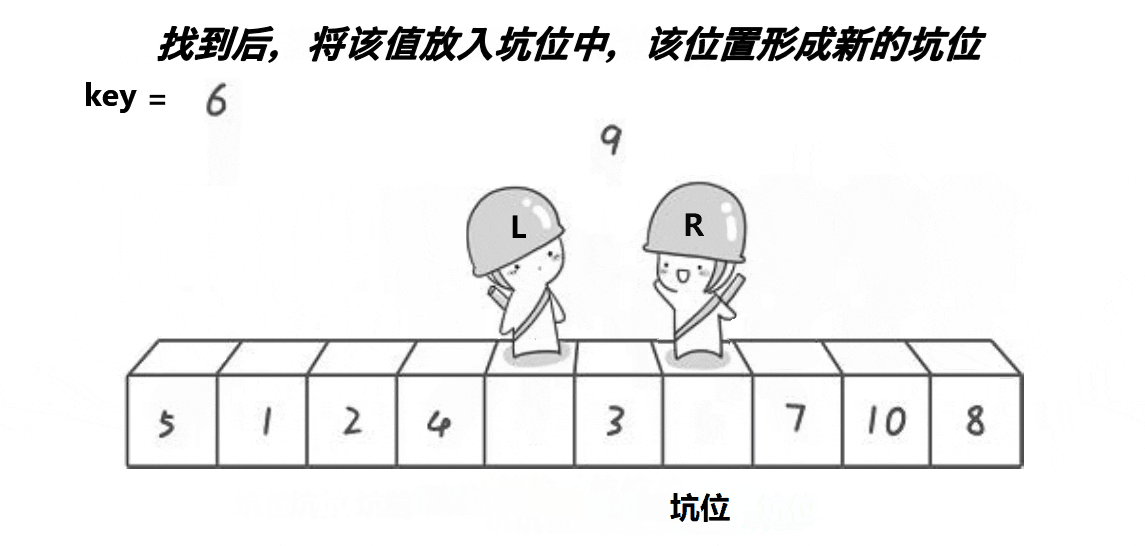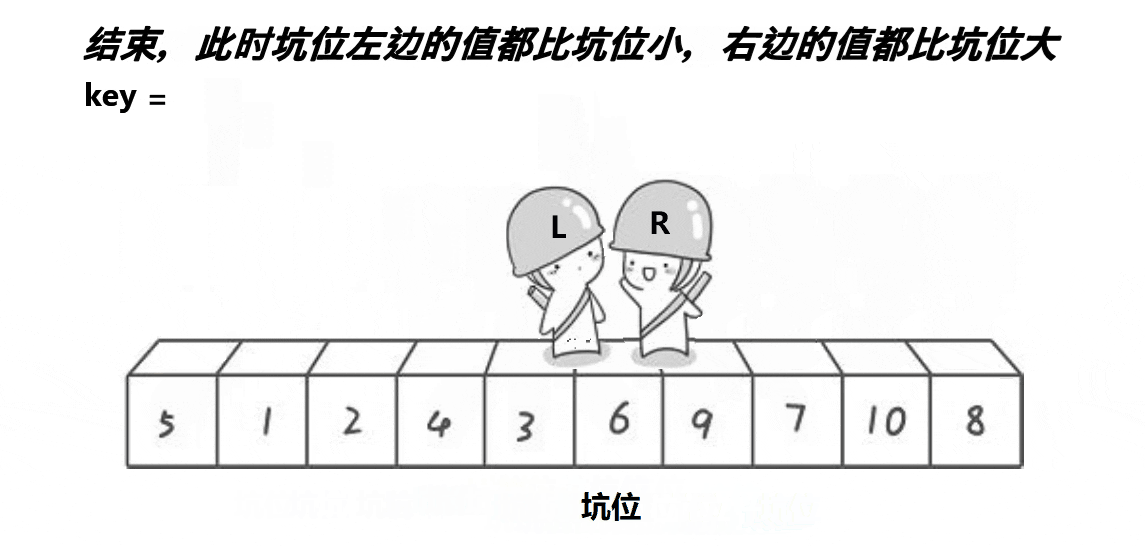
[头歌系统数据库实验] 实验3 MySQL的DDL语言
目录 第1关:将P表中的所有红色零件的重量增加6 第2关:把P表中全部红色零件的颜色改成蓝色 第3关:将SPJ表中由S5供给J4的零件P6改为由S3供应 第4关:将SPJ表中所有天津供应商的QTY属性值减少11(用子查询方式&#x…...

系统运维安全之病毒自检及防护
一、前言 Linux勒索病毒(Linux ransomware)是一种最令人恶心的计算机恶意病毒,它以侵入Linux系统,捆绑文件并要求支付赎金才能释放文件为主要目的,破坏用户的数据,造成数据讹诈。Linux勒索病毒它们的存在已…...
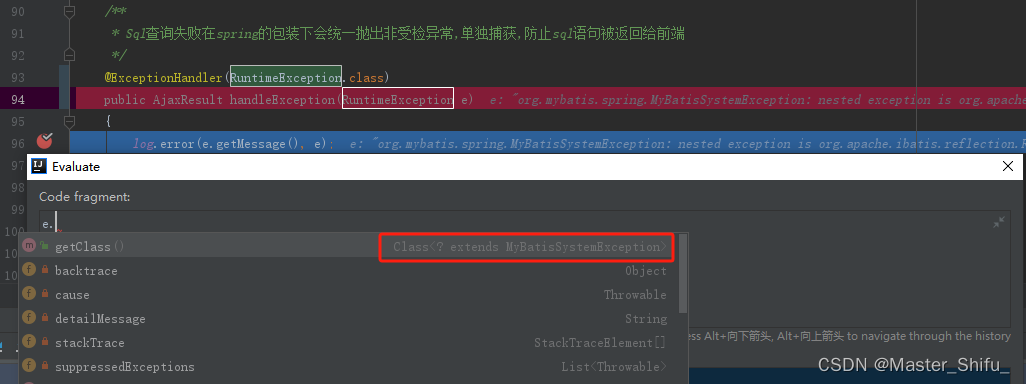
Mabatis处理异常屏蔽SQL返回前端全局异常捕获处理
文章目录 Mabatis处理异常屏蔽SQL返回前端全局异常捕获处理结论1 java异常体系2 Spring框架异常处理3 定位Spring框架转化为哪种unchecked异常3.1 捕获RuntimeException定位Spring框架转化抛出的异常类3.2 进一步查看包名判断3.3 识别MyBatisSystemException下级实现3.3 识别My…...
黑豹程序员-java发邮件,发送内容支持html,带多附件的案例
介绍 发邮件mail是常见的软件功能,下面利于spring和java的mail库实现发送内容支持html,带多附件的案例 开启SMTP邮件发送协议 谁提供的SMTP邮件服务,就找谁开启。QQ邮箱类似。 依赖 <!--Java MAil 发送邮件API--><dependency&g…...

[LeetCode] 15. 三数之和
15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 **注意:**答案中不可以包含重复…...
Android Chips(标签)
目录 一、流式布局标签发展历程 二、类型及使用 2.1 Chip.Action(默认值) 2.2 Chip.Entry 2.3 Chip.Filter 2.4 Chip.Choice 三、常用事件 3.1 OnClickListener 3.2 OnCheckedChangeListener 3.3 OnCloseIconClickListener 四、ChipGroup 4.1 ChipGroup Chip.Choi…...
飞行汽车开发原理(上)
前言 小节的安排是由浅入深,要按顺序读;有电路知识基础的同学可跳到“计算机电路”一节开始。因为知识点之间有网状依赖,没办法按分类来讲。 为了避免过于深入、越讲越懵,很多描述仅为方便理解、不求严谨。 半导体特性 导体&a…...

22、pytest多个参数化的组合
官方实例 # content of test_multi_parametrie.py import pytestpytest.mark.parametrize("x",[0,1]) pytest.mark.parametrize("y",[2,3]) def test_foo(x,y):print("{}-{}".format(x,y))pass解读与实操 要获得多个参数化参数的所有组合&…...

【网络奇缘】- 如何自己动手做一个五类|以太网|RJ45|网络电缆
🌈个人主页: Aileen_0v0🔥系列专栏: 一见倾心,再见倾城 --- 计算机网络~💫个人格言:"没有罗马,那就自己创造罗马~" 本篇文章关于计算机网络的动手小实验---如何自己动手做一个网线, 也是为后面的物理层学习进…...

【从零开始学习JVM | 第三篇】类的生命周期(高频面试)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。 在本文中,我们将深入探讨类的生命周期,从类加载到…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
