【数据结构】二叉树的实现
目录
- 1. 前言
- 2. 二叉树的实现
- 2.1 创建一棵树
- 2.2 前序遍历
- 2.2.1 分析
- 2.2.2 代码实现
- 2.2.3 递归展开图
- 2.3 中序遍历
- 2.3.1 分析
- 2.3.2 代码实现
- 2.3.3 递归展开图
- 2.4 后序遍历
- 2.4.1 分析
- 2.4.2 代码实现
- 2.4.3 递归展开图
- 2.5 求节点个数
- 2.5.1 分析
- 2.5.2 代码实现
- 2.6 求叶子节点个数
- 2.6.1 分析
- 2.6.2 代码实现
- 2.7 求树高度
- 2.7.1 分析
- 2.7.2 代码实现
- 2.8 求第K层节点的个数
- 2.8.1 分析
- 2.8.2 代码实现
1. 前言
在前面的博客中写了有关二叉树的介绍,那这次来写关于用C语言来实现与二叉树有关的一些操作。
与之前链表和顺序表不同的是,这里不实现增删查改。
2. 二叉树的实现
2.1 创建一棵树
直接手动创建一棵树,也就是直接malloc所有的节点。
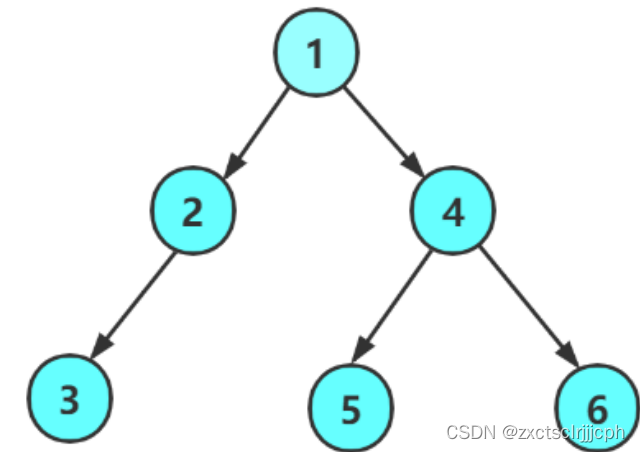
直接创建6个节点,然后让node1的数据直接是1,让node2的数据直接是2,依次下去。
然后直接让node1的left = node2,它的right = node4;就按照上面的图来构建。
代码如下:
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}TreeNode;TreeNode* CreateTree()
{TreeNode* node1 = (TreeNode*)malloc(sizeof(TreeNode));assert(node1);TreeNode* node2 = (TreeNode*)malloc(sizeof(TreeNode));assert(node2);TreeNode* node3 = (TreeNode*)malloc(sizeof(TreeNode));assert(node3);TreeNode* node4 = (TreeNode*)malloc(sizeof(TreeNode));assert(node4);TreeNode* node5 = (TreeNode*)malloc(sizeof(TreeNode));assert(node5);TreeNode* node6 = (TreeNode*)malloc(sizeof(TreeNode));assert(node6);node1->data = 1;node2->data = 2;node3->data = 3;node4->data = 4;node5->data = 5;node6->data = 6;node1->left = node2;node1->right = node4;node2->left = node3;node2->right = NULL;node3->left = NULL;node3->right = NULL;node4->left = node5;node4->right = node6;node5->left = NULL;node5->right = NULL;node6->left = NULL;node6->right = NULL;
}
但是这个代码局限性太大,已经是写固定了的代码,不好再修改,下面这种会好一些。
不用管空。
想要其它形状的可以修改代码,做一定的增加或者就行。
代码如下:
TreeNode* BuyTreeNode(int x)
{TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));assert(node);node->data = x;node->left = NULL;node->right = NULL;return node;
}TreeNode* CreateTree()
{TreeNode* node1 = BuyTreeNode(1);TreeNode* node2 = BuyTreeNode(2);TreeNode* node3 = BuyTreeNode(3);TreeNode* node4 = BuyTreeNode(4);TreeNode* node5 = BuyTreeNode(5);TreeNode* node6 = BuyTreeNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}
2.2 前序遍历
2.2.1 分析
前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。

就实现这颗树的前序遍历。
先根,然后左子树,再右子树,初学时把NULL也带上,方便理解。
也就是下面这样。

先访问根,然后找左子树,左子树又得拆成根和左子树,一直到空。使用递归来实现。
2.2.2 代码实现
void PrevOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}
结果和分析的一样:
2.2.3 递归展开图
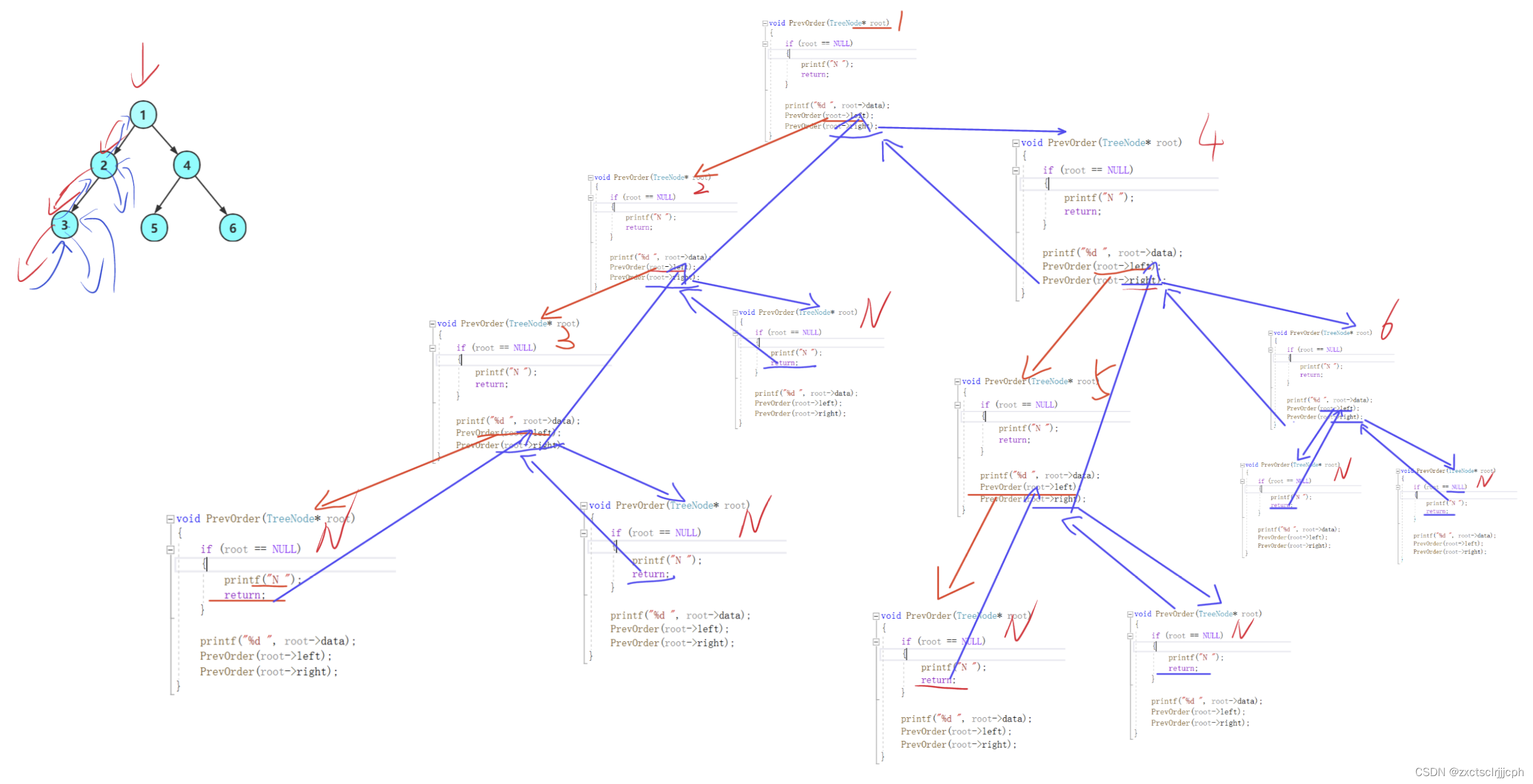
2.3 中序遍历
2.3.1 分析
中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
同样以上面那棵树为例子。
先左子树,再根,再右子树。

这里遇到根先不是NULL,先走它的左子树,是空就打印返回。
2.3.2 代码实现
void InOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
结果与分析的是一样的:

2.3.3 递归展开图
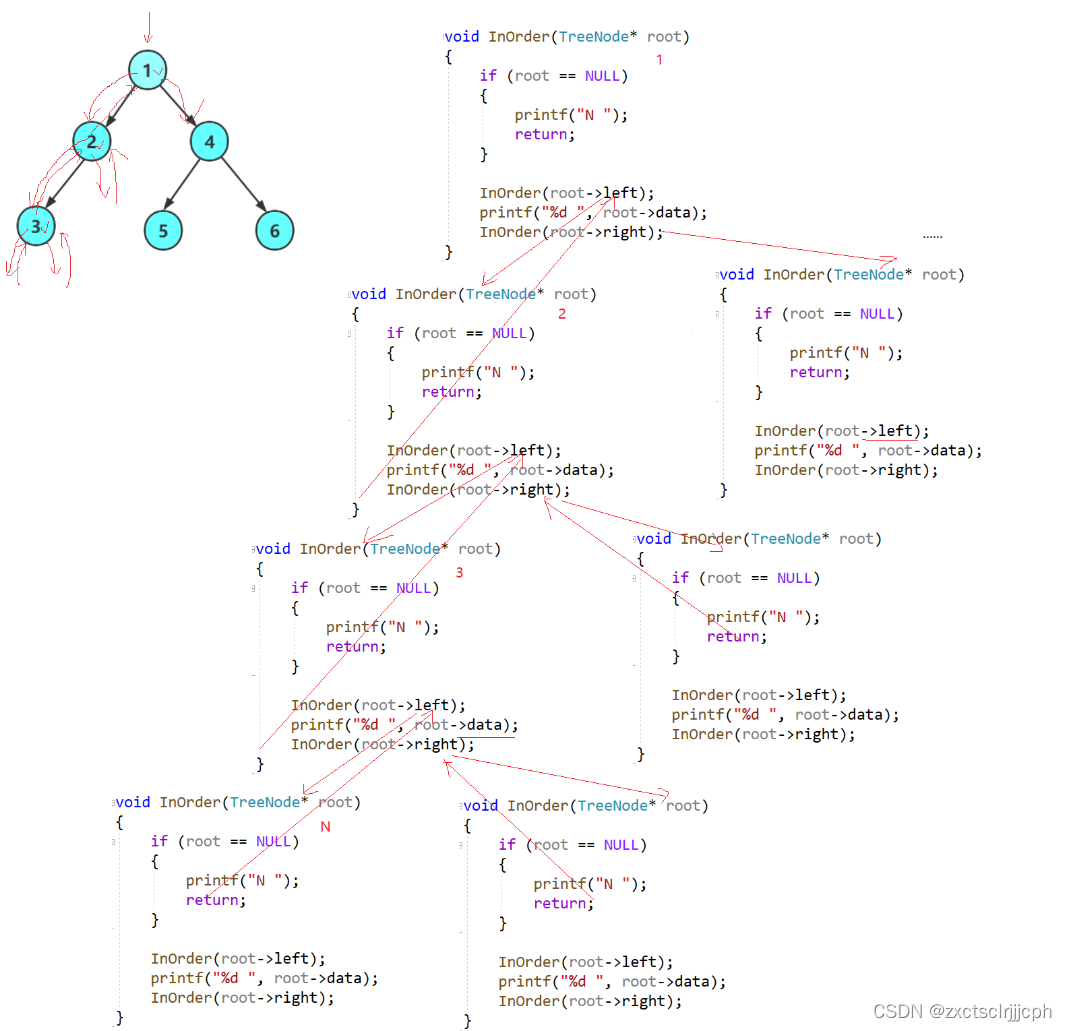
2.4 后序遍历
2.4.1 分析
.后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
同样是以上面那棵树为例子,它的后序遍历就是:

先访问它的左子树,然后右子树,最后才是根。
要当左右都为空时才访问第一个节点。
2.4.2 代码实现
void PostOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}
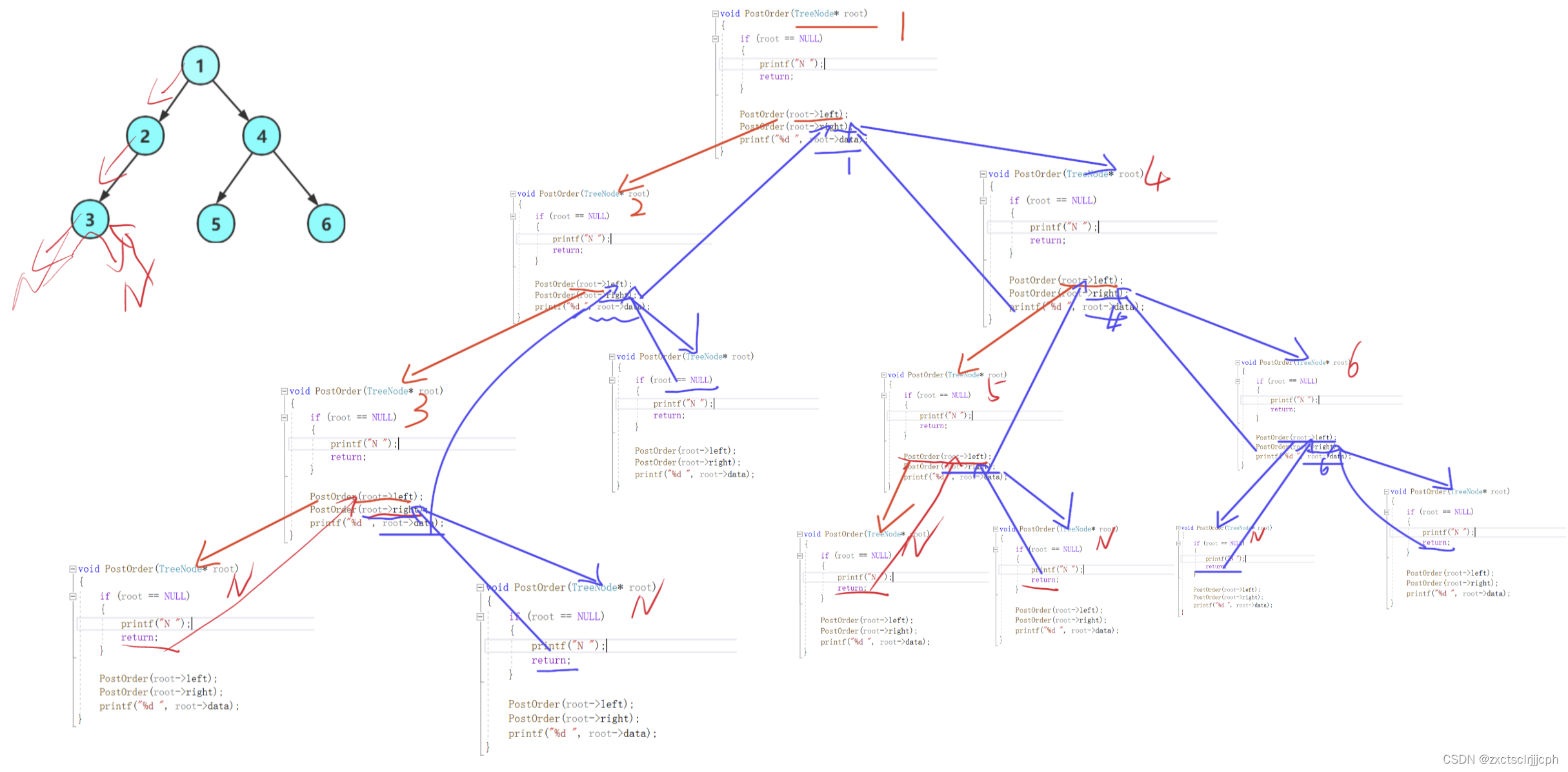
递归展开方式也是一样的
2.4.3 递归展开图
2.5 求节点个数
2.5.1 分析
只要节点不为空,就加加,然后再调用左子树,右子树。
用全局的size,每次调用前先置空一些。
局部的使用不了,因为不能置空,再调用一次就会再上次的基础上累计。

同样是这课树节点数为6。
2.5.2 代码实现
int size = 0;
void TreeSize(TreeNode* root)
{if (root == NULL)return;++size;TreeSize(root->left);TreeSize(root->right);
}int main()
{ TreeNode* root = CreateTree();size = 0;TreeSize(root);printf("TreeSize:%d\n", size);return 0;
}

还有另一种实现:把树拆成左子树加右子树加1.
代码如下:
int TreeSize(TreeNode* root)
{return root == NULL ? 0 :TreeSize(root->left) +TreeSize(root->right) + 1;
}
结果还是一样的。

采用的就是分治法
2.6 求叶子节点个数
2.6.1 分析
先得判断一下树是不是空树,不是才能就行进行。
不是空树,而且左右节点都为空,就是叶子节点,就返回1;
不是空,也不是叶子节点就采用分治,树的节点就等于左右叶子节点的和。


同样是这棵树,叶子节点就是3.
2.6.2 代码实现
int TreeLeafSize(TreeNode* root)
{// 空 返回0if (root == NULL)return 0;// 不是空,是叶子 返回1if (root->left == NULL&& root->right == NULL)return 1;// 不是空 也不是叶子 分治=左右子树叶子之和return TreeLeafSize(root->left) +TreeLeafSize(root->right);
}
int main()
{TreeNode* root = CreateTree();printf("TreeLeafSize:%d\n", TreeLeafSize(root));return 0;
}和分析的一样叶子节点个数就是3.
2.7 求树高度
2.7.1 分析
先要判断一下树是不是空树,是就为0。
不是空树,就要判断一下左子树和右子树那个更高,然后高的那个就加1。

同样以这棵树计算,这棵树的高度就是3
2.7.2 代码实现
int TreeHeight(TreeNode* root)
{if (root == NULL)return 0;int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}int main()
{TreeNode* root = CreateTree();printf("TreeHeight:%d\n", TreeHeight(root));return 0;
}
int TreeHeight(TreeNode* root)
{if (root == NULL)return 0;return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
}
这里使用fmax返回大的数,需要包一个头文件<math.h>
结果也是一样的。
2.8 求第K层节点的个数
2.8.1 分析
同样采用分治。
如果是空树就返回0;
如果不为空,k=1,第一层就返回1;
如果不为空,且k>1,就返回左子树的k-1层加上右子树的k-1层。
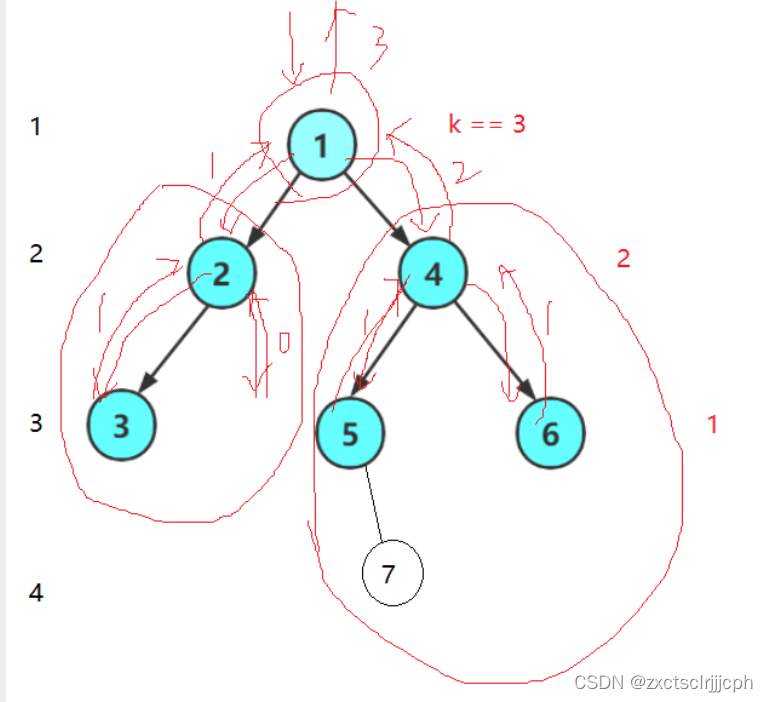
同样以这棵树计算,k>1就说明再第一层的下面。这棵树的第三层的节点数就是,第二层的左加第二层的右;第二层的左又转化成第一层的左加第一层的右,为空就返回0。
2.8.2 代码实现
int TreeLevelK(TreeNode* root, int k)
{assert(k > 0);if (root == NULL)return 0;if (k == 1)return 1;return TreeLevelK(root->left, k - 1)+ TreeLevelK(root->right, k - 1);
}
int main()
{TreeNode* root = CreateTree();printf("TreeLevelK:%d\n", TreeLevelK(root, 3));return 0;
}
结果如下:
有问题请指出,大家一起进步!
相关文章:

【数据结构】二叉树的实现
目录 1. 前言2. 二叉树的实现2.1 创建一棵树2.2 前序遍历2.2.1 分析2.2.2 代码实现2.2.3 递归展开图 2.3 中序遍历2.3.1 分析2.3.2 代码实现2.3.3 递归展开图 2.4 后序遍历2.4.1 分析2.4.2 代码实现2.4.3 递归展开图 2.5 求节点个数2.5.1 分析2.5.2 代码实现 2.6 求叶子节点个数…...

振弦采集仪在土体与岩体监测中的可靠性与精度分析
振弦采集仪在土体与岩体监测中的可靠性与精度分析 振弦采集仪是一种用于土体和岩体监测的重要设备,它可以通过测量振动信号来获取土体或岩体的力学参数,如应力、应变、弹性模量等。而振弦采集仪的可靠性和精度是影响其应用效果的关键因素。 首先&#x…...

C语言进阶之路-指针、数组等混合小boss篇
目录 一、学习目标: 二、指针、数组的组合技能 引言 指针数组 语法 数组指针 三、勇士闯关秘籍 四、大杂脍 总结 一、学习目标: 知识点: 明确指针数组的用法和特点掌握数组指针的用法和特点回顾循环等小怪用法和特点 二、指针、数…...

【矩阵论】Chapter 7—Hermite矩阵与正定矩阵知识点总结复习
文章目录 1 Hermite矩阵2 Hermite二次型3 Hermite正定(非负定矩阵)4 矩阵不等式 1 Hermite矩阵 定义 设 A A A为 n n n阶方阵,如果称 A A A为Hermite矩阵,则需满足 A H A A^HA AHA,其中 A H A^H AH表示 A A A的共轭转…...

Golang语言基础之切片
概述 数组的长度是固定的并且数组长度属于类型的一部分,所以数组有很多的局限性 func arraySum(x [3]int) int{sum : 0for _, v : range x{sum sum v}return sum } 这个求和函数只能接受 [3]int 类型,其他的都不支持。 切片 切片(Slic…...

SpringCloud-服务消费者Fegin调用时无法获取异常信息
一、前言 假设有以下需求: 服务消费者A调用服务提供者B往MySQL新增一条人员信息服务提供者做了一个逻辑判断:若无该人员信息则新增,若已存在该人员信息,则返回给消费者异常状态码及异常信息:“请勿添加重复数据” 问…...
re:invent 2023 Amazon Q 初体验
授权声明:本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 Developer Centre,知乎,自媒体平台,第三方开发者媒体等亚马逊云科技官方渠道 前言 亚马逊云科技在2023 re:Invent全球大会上宣布推出 Amazon…...
认知觉醒(四)
认知觉醒(四) 第三节 耐心:得耐心者得天下 20世纪八九十年代,金庸的武侠小说风靡全国。如今,虽然几十年过去了,金庸先生也已与世长辞,但他留下的作品依然广受欢迎,被奉为经典。如此成就,自然…...
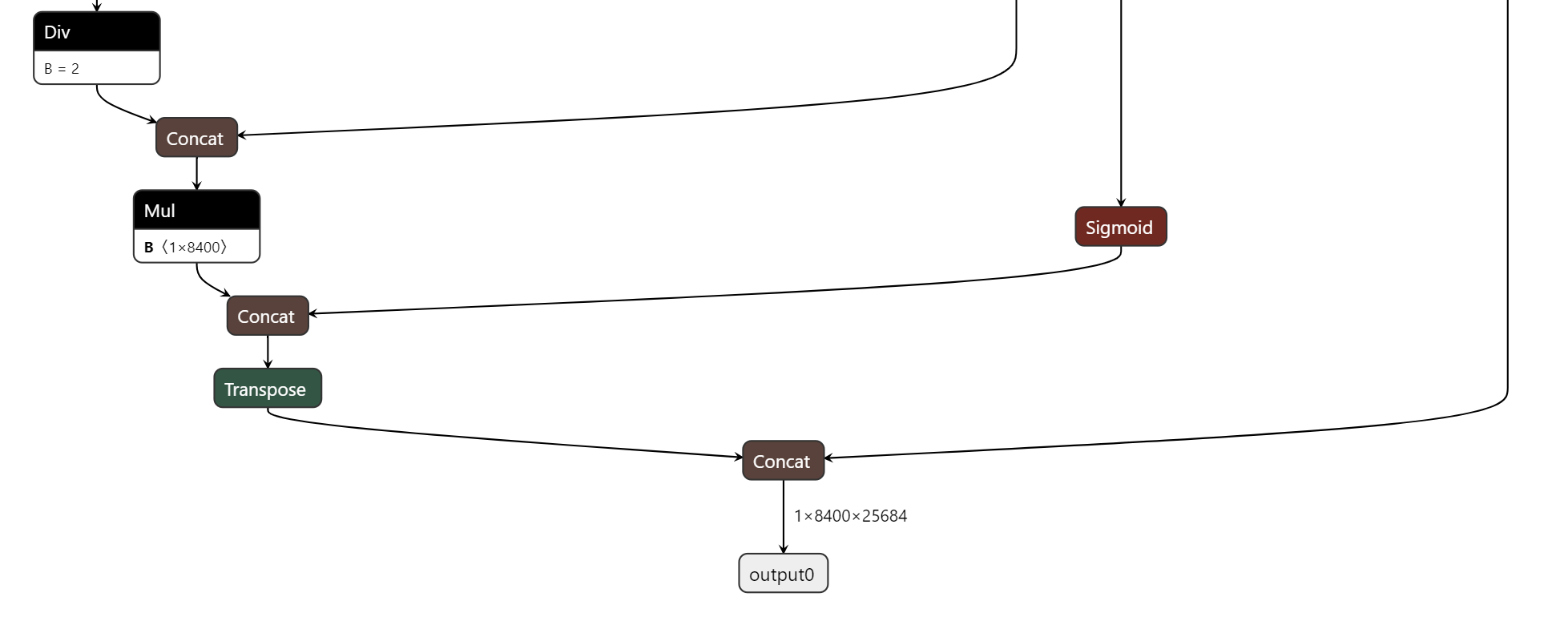
AI模型部署 | onnxruntime部署YOLOv8分割模型详细教程
本文首发于公众号【DeepDriving】,欢迎关注。 0. 引言 我之前写的文章《基于YOLOv8分割模型实现垃圾识别》介绍了如何使用YOLOv8分割模型来实现垃圾识别,主要是介绍如何用自定义的数据集来训练YOLOv8分割模型。那么训练好的模型该如何部署呢?…...

模拟电路学习笔记(一)之芯片篇(持续更新)
模拟电路学习笔记(一)之芯片篇(持续更新) 1.CD4047BE芯片 CD4047是一种包含高电压的多谐振荡器,该器件的操作可以在两种模式下完成,分别是单稳态和非稳态。CD4047需要一个外部电阻器和电容器来决定单稳态…...

如何利用CentOS7+docker+jenkins+gitee部署springboot+vue前后端项目(保姆教程)
博主介绍:Java领域优质创作者,博客之星城市赛道TOP20、专注于前端流行技术框架、Java后端技术领域、项目实战运维以及GIS地理信息领域。 🍅文末获取源码下载地址🍅 👇🏻 精彩专栏推荐订阅👇🏻…...

qt 5.15.2 主窗体事件及绘制功能
qt 5.15.2 主窗体事件及绘制功能 显示主窗体效果图如下所示: main.cpp #include "mainwindow.h"#include <QApplication>int main(int argc, char *argv[]) {QApplication a(argc, argv);MainWindow w;w.setFixedWidth(600);w.setFixedHeight(6…...

(2)(2.4) TerraRanger Tower/Tower EVO(360度)
文章目录 前言 1 安装传感器并连接 2 通过地面站进行配置 3 参数说明 前言 TeraRanger Tower 可用于在 Loiter 和 AltHold 模式下进行目标规避。传感器的最大可用距离约为 4.5m。 TeraRanger Tower EVO 可用于在 Loiter 和 AltHold 模式下进行目标规避。传感器的最大可用…...

Redis_主从复制、哨兵模式、集群模式详解
Redis的主从复制 为什么Redis要引入主从复制?what? 在这里博主为小伙伴们简单的做下解释,可以了解一下 实际生产环境下,单机的redis服务器是无法满足实际的生产需求的。 第一,单机的redis服务器很容易发生单点故障&am…...
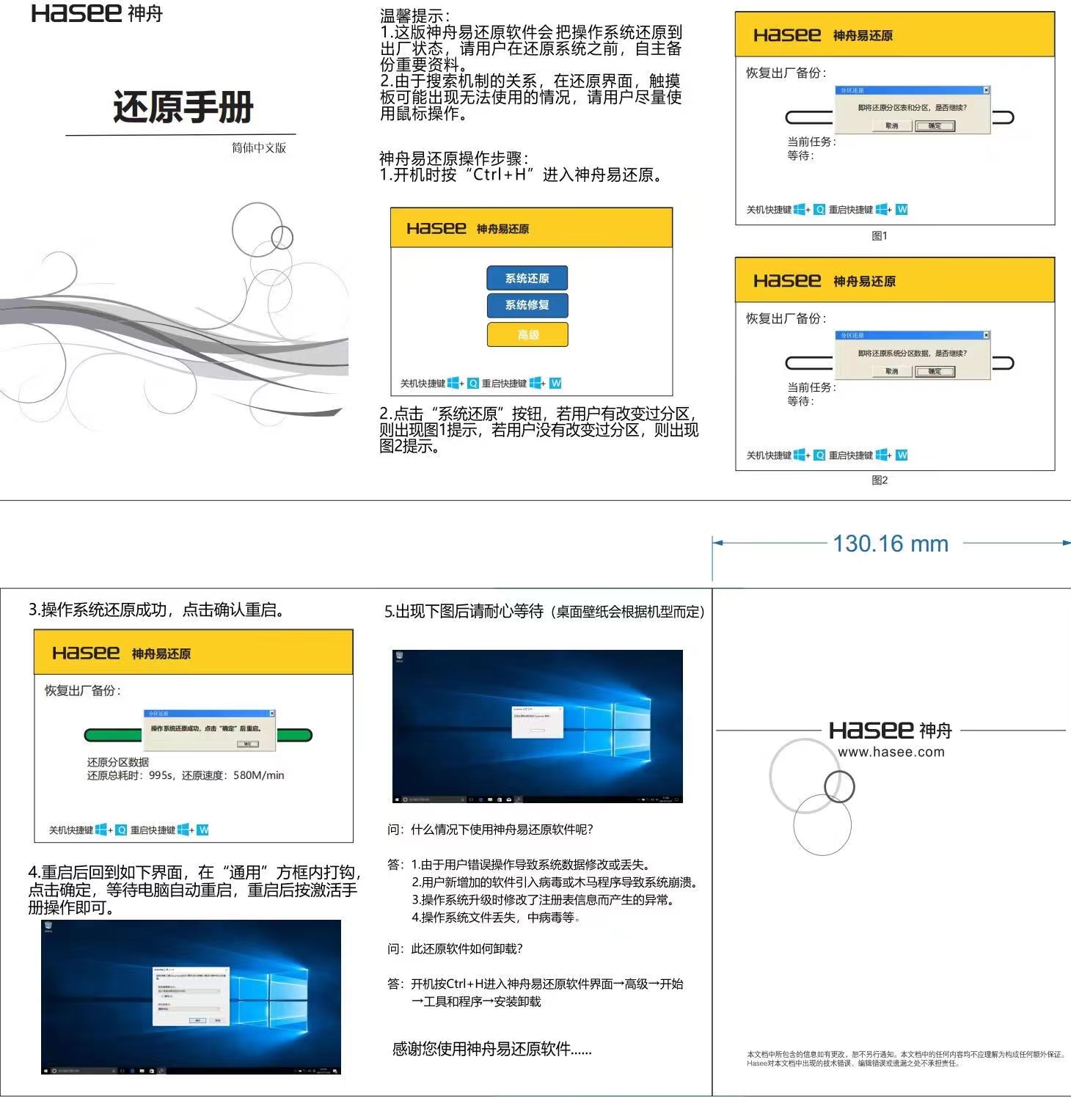
关于神舟-战神TA5NS系统重装问题
加装固态卡在log处无法开机问题 下面是我的步骤 1.按f7选择pe安装系统,然后发现卡在战神log处不转动 2.下载驱动 TA5NS驱动地址 下载RAID驱动(如果没有私信我,我网盘里有),拷到u盘中,然后进入pe系统里面…...
前端大文件上传webuploader(react + umi)
使用WebUploader还可以批量上传文件、支持缩略图等等众多参数选项可设置,以及多个事件方法可调用,你可以随心所欲的定制你要的上传组件。 分片上传 1.什么是分片上传 分片上传,就是将所要上传的文件,按照一定的大小,将…...
数据库常用sql命令)
人大金仓(kingbase)数据库常用sql命令
一. 字段 1. 添加 alter table book add column book_id varchar not null, book_title varchar(10) default ;2. 删除 alter table book drop book_id, book_title;// 外键时 alter table book drop book_id, book_title cascade;3. 修改类型 alter table book alter colu…...

HashMap相关专题
前置知识:异或运算 异或运算介绍 异或有什么神奇之处(应用)? (1)快速比较两个值 (2)我们可以使用异或来使某些特定的位翻转,因为不管是0或者是1与1做异或将得到原值的相…...

threejs WebGLRenderer 像素比对画布大小的影响
官方文档 - WebGLRenderer .setPixelRatio ( value : number ) : undefined 设置设备像素比。通常用于避免HiDPI设备上绘图模糊 .setSize ( width : Integer, height : Integer, updateStyle : Boolean ) : undefined 将输出canvas的大小调整为(width, height)并考虑设备像素比…...
 与 RocketMQTemplate.syncSend() 方法详解)
RocketMQTemplate.send() 与 RocketMQTemplate.syncSend() 方法详解
Apache RocketMQ 是一款强大的分布式消息中间件,与 Spring Boot 集成后,通过 RocketMQTemplate 提供了多种方法来发送消息。其中,send() 和 syncSend() 是两个常用的发送消息方法,本文将深入探讨它们的区别以及详细解释这两个方法…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
