WeakMap
WeakMap简介
作为es6一种新的数据结构,他是一种键值对的集合。与Map最大的区别有两个
1. 是其中的键必须是对象或非全局注册的符号。
全局注册的符号
const s1 = Symbol.for('mySymbol')
非全局注册的符号
const s1 = Symbol('mySymbol')
了解Symbol.for
2. 不会创建对它的键的强引用
不会像变量一样随着作用域的销毁而被清除就是强引用
一个对象作为 WeakMap 的键存在,不会阻止该对象被垃圾回收。当该对象的所有强引用都销毁时,该对象的弱引用也随之自动被清除。那么就会在 WeakMap 中相应的值便成为了进行垃圾回收的候选对象,只要它们没有其他的引用存在。
我们使用Map做下简单对比
let map = new Map()
let key = { name: 1 }
map.set(key, '我的键是一个对象')
key = null
setTimeout(() => {console.log(map) //无论延迟多久,map里面的键值对都会存在
}, 10000);
let wMap = new WeakMap()
let key2 = { name: 1 }
wMap.set(key2, '我的键是一个对象')
key2 = null
setTimeout(() => {console.log(wMap) //会被浏览器的回收机制回收(测试edge浏览器十秒回收),WeakMap里面的键值对已经清空。
}, 10000);
可以看到在使用Map创建的对象里,即使key对象和map对象已经没有任何地方使用,甚至我们将key设置为了null,但是在内存里,{name: 1}依旧会存在,因为在map对象中的键依旧对它有着强引用的关系。
而我们使用的WeakMap创建的对象,当我们将key2设置为bull后,因为wMap的键是弱引用的关系,所以该键值会直接被垃圾回收机制回收,该键值对会直接被清除。
常见方法
delete
删除任何与 key 关联的值。删除之后,WeakMap.prototype.has(key) 将会返回 false。
get
返回与 key 关联的值,如果不存在则返回 undefined。
has
返回一个布尔值,断言某个值是否已经与 WeakMap 对象中的 key 关联。
set
给 WeakMap 对象中的 key 设置 value。返回该 WeakMap 对象。
应用场景
-
Vue 3 的响应式系统使用了 Proxy 对象来拦截对响应式对象的访问,然后在内部使用 WeakMap 来跟踪对象与其对应的副作用(例如渲染函数或侦听器)。这样,当响应式对象发生变化时,Vue 3 可以根据这些依赖关系自动进行更新。
通过 WeakMap,Vue 3 实现了一种弱引用关系,这意味着如果一个对象不再被其他地方引用,它将被垃圾回收机制自动回收,同时也会自动清理相应的依赖关系。 -
WeakMap还常常被用来保存对象的私有数据。这是因为WeakMap的键不可遍历,所以我们可以利用这个特性来存储一些只有特定代码能够访问的数据。

上面是一个人们经常拿来说明WeakMap应用场景的一个方法,但实际上描述并不完全正确。
实际上WeakMap 方式定义私有属性的主要作用是保护属性的名称,防止和其他实例的同名属性发生冲突。但不能保证属性的值不被修改。使用getPrivateVal方法外还可以直接使用privateData.get(obj)的方式进行访问甚至对值进行修改。
- 曾经看到使用WeakMap进行栈的模拟实现
let Stack = (function(){let items = new WeakMap()class Stack {constructor () {items.set(this, [])}pop () { // 出栈return items.get(this).pop()}push (v) { // 入栈items.get(this).push(v)}peek () { // 获取当前栈顶return items.get(this)[items.get(this).length - 1]}size () { // 栈长度return items.get(this).length}isEmpty () { // 栈是否为空return items.get(this).length === 0}clear () { // 清空栈items.get(this).length = 0}}return Stack
})()
相关文章:

WeakMap
WeakMap简介 作为es6一种新的数据结构,他是一种键值对的集合。与Map最大的区别有两个 1. 是其中的键必须是对象或非全局注册的符号。 全局注册的符号 const s1 Symbol.for(mySymbol) 非全局注册的符号 const s1 Symbol(mySymbol)了解Symbol.for 2. 不会创建对它…...
获取网络ppt资源
背景: 某度上有很多优质的PPT资源和文档资源,但是大多数需要付费才能获取。对于一些经济有限的用户来说,这无疑是个遗憾,因为我们更倾向于以免费的方式获取所需资源。 解决方案: 然而,幸运的是&am…...
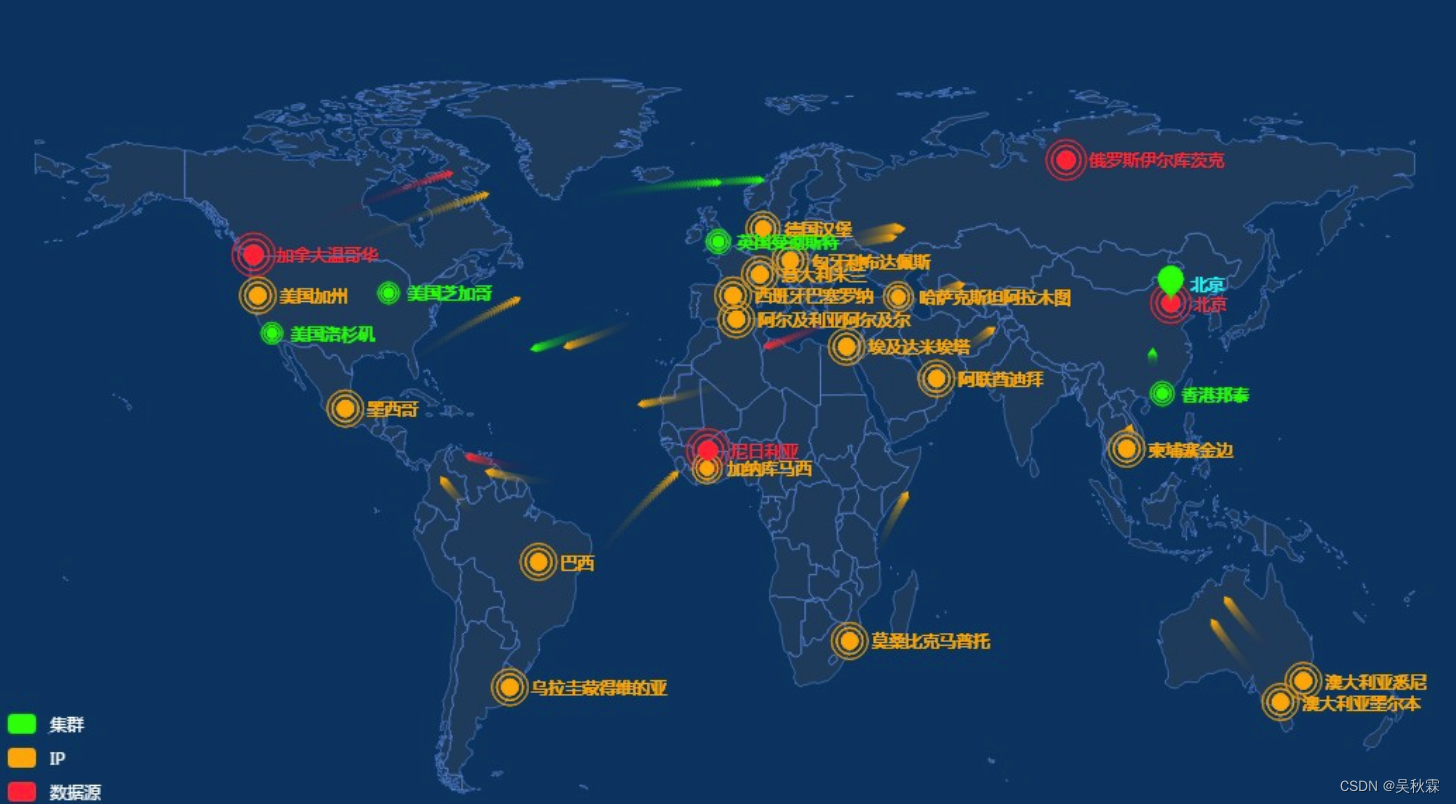
从0到1构建智能分布式大数据爬虫系统
文章目录 1. 写在前面2. 数据获取挑战3. 基础架构4. 爬取管理5. 数据采集6. 增量与去重设计 【作者主页】:吴秋霖 【作者介绍】:Python领域优质创作者、阿里云博客专家、华为云享专家。长期致力于Python与爬虫领域研究与开发工作! 【作者推荐…...
)
C语言速通笔记(41-62)
40.十六进制转义字符:\x6d才是合法的,前面的0不能写,而且 x 是小写 41.字符型和整型是近亲:两个具有很大的相似之处,所有的字符都有一个它对应的整形数 据的 ASCLL 的数值。如 char a 65 % …...
Python 调用企业微信群机器人发送消息及文件
Python 操作企业微信群机器人。 企业微信群创建机器人 : 安装 requests json : pip install requests pip install json发送消息(markdown) import requests import json# 企业微信机器人发送文字 def send_markdown (message, …...

数据结构:链表应用:第6关:链表的分解
任务描述 本关任务:利用单链表A表示一个非零整数序列,把A分解为两个具有相同结构的链表B和C,其中B表的结点为A表中值小于零的结点,而C表的结点为A表中值大于零的结点。要求空间复杂度为O(1),链表B和C均利用链表A的结点…...
与留一法(Leave-One-Out))
10折交叉验证(10-fold Cross Validation)与留一法(Leave-One-Out)
概念: 交叉验证法,就是把一个大的数据集分为 k个小数据集,其中 k − 1 个作为训练集,剩下的 1 个作为测试集,在训练和测试的时候依次选择训练集和它对应的测试集。这种方法也被叫做 k 折交叉验证法(k-fold…...
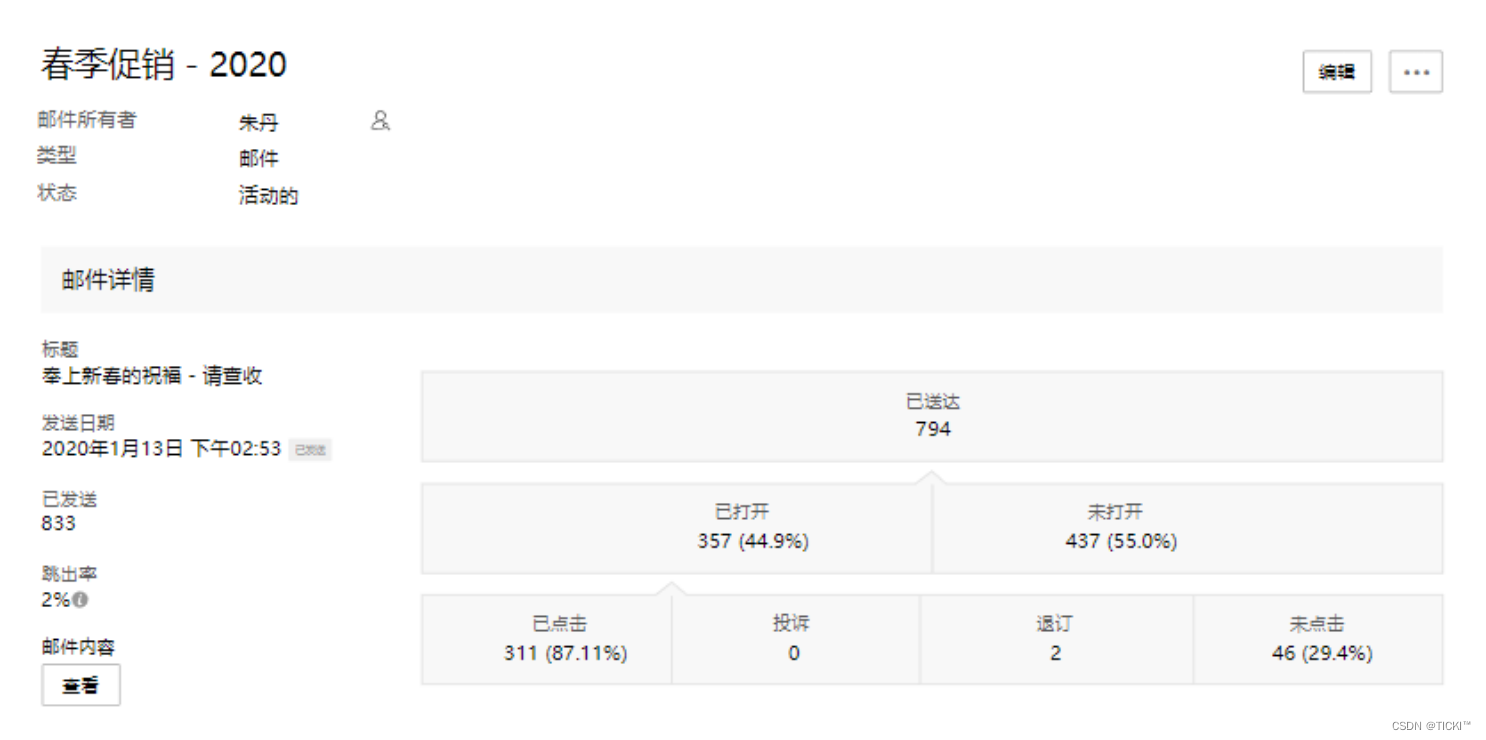
中小企业:理解CRM与ERP系统的区别与联系,提升业务效能
许多中小型企业正面临着客户递增,市场营销,货存流通等递增数据整合的困扰。这个时候需要根据自身企业的实际情况去选择适合自己的系统。那么,中小企业使用CRM系统和erp系统的区别是什么? 一、含义和目标区别 CRM系统旨在帮助企业…...
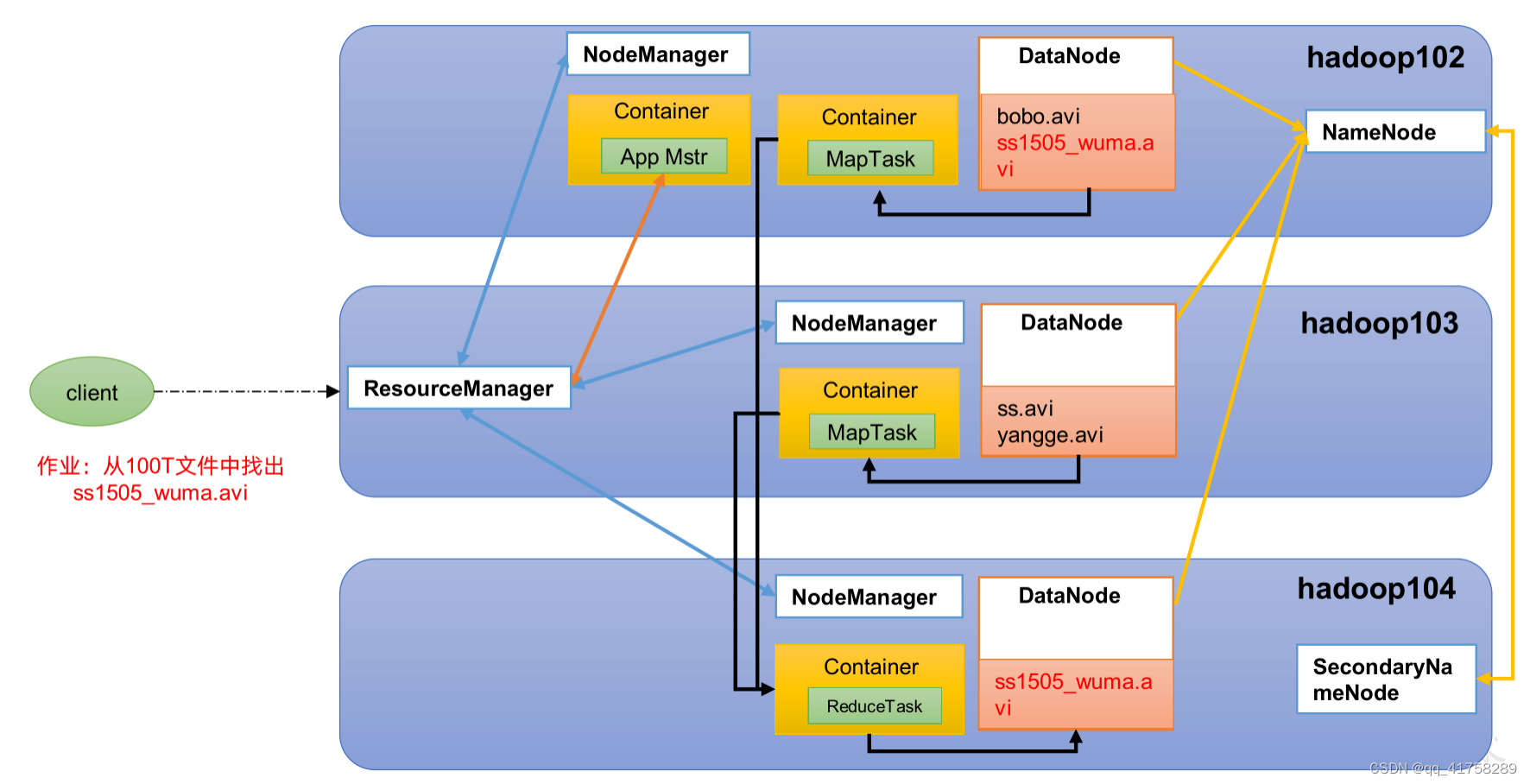
01数仓平台 Hadoop介绍与安装
Hadoop概述 Hadoop 是数仓平台的核心组件。 在 Hadoop1.x 时代,Hadoop 中的 MapReduce 同时处理业务逻辑运算和资源调度,耦合性较大。在 Hadoop2.x 时代,增加了 Yarn。Yarn 只负责资源的调度,MapReduce 只负责运算。Hadoop3.x 在…...

网络编程HTTP协议进化史
一、Http报文格式 具有约定格式的数据块 请求报文 request 状态行:本次请求的请求方式(post get)资源路径url http 协议的版本号,中间用空格划分 本次请求的请求方式(post get)资源路径url http 协议…...

第17章 匿名函数
第17.1节 匿名函数的基本语法 [捕获列表](参数列表) mutable(可选) 异常属性 -> 返回类型 { // 函数体 }语法规则:lambda表达式可以看成是一般函数的函数名被略去,返回值使用了一个 -> 的形式表示。唯一与普通函数不同的是增加了“捕获列表”。 …...

JVM虚拟机:JVM参数之标配参数
本文重点 本文我们将学习JVM中的标配参数 标配参数 从jdk刚开始就有的参数,比如: -version -help -showversion...

UEC++ 探索虚幻5笔记(捡金币案例) day12
吃金币案例 创建金币逻辑 之前的MyActor_One.cpp,直接添加几个资源拿着就用 //静态网格UPROPERTY(VisibleAnywhere, BlueprintReadOnly)class UStaticMeshComponent* StaticMesh;//球形碰撞体UPROPERTY(VisibleAnywhere, BlueprintReadWrite)class USphereCompone…...

Docker 安装 Redis 挂载配置
1. 创建挂载文件目录 mkdir -p /home/redis/config mkdir -p /home/redis/data # 创建配置文件:docker容器中默认不包含配置文件 touch /home/redis/config/redis.conf2. 书写配置文件 # Redis 服务器配置# 绑定的 IP 地址,默认为本地回环地址 127.0.0…...
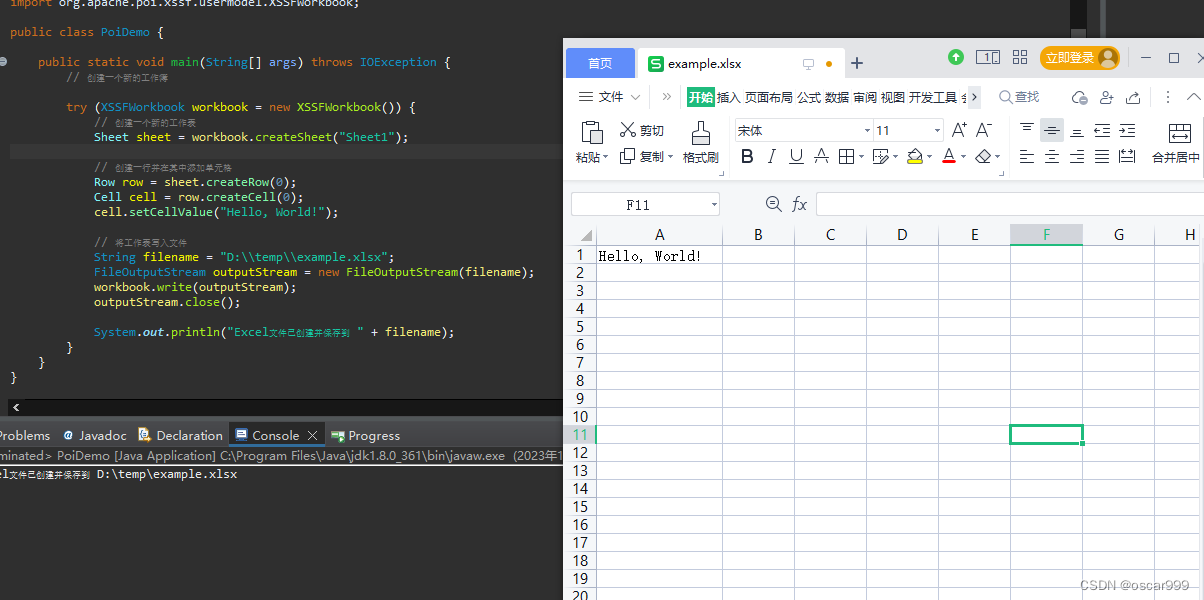
Java操作Excel之 POI介绍和入门
POI是Apache 提供的一个开源的Java API,用于操作Microsoft文档格式,如Excel、Word和PowerPoint等。POI是Java中处理Microsoft文档最受欢迎的库。 截至2023/12, 最新版本时 POI 5.2.5。 JDK版本兼容 POI版本JDK版本4.0及之上版本> 1.83.…...

麒麟v10 数据盘初始化 gpt分区
麒麟v10 数据盘初始化 gpt分区 1、查看磁盘 lsblk2 、分区 parted2.1、 设置磁盘分区形式2.2、 设置磁盘的计量单位为磁柱2.3、 分区2.4、 查看分区 3、分区格式化4、 挂载磁盘4.1、新建挂载目录4.2、挂载磁盘4.3、查看挂载结果 5、设置开机自动挂载磁盘分区5.1、 查询磁盘分区…...

php时间和centos时间不一致
PHP 时间和 CentOS 操作系统时间不一致的问题通常是由于时区设置不同造成的。解决这个问题可以通过以下几个步骤: 检查 CentOS 系统时间: 你可以通过在终端运行命令 date 来查看当前的系统时间和时区。 配置 CentOS 的时区: 如果系统时间不正…...

软件工程 复习笔记
目录 概述 软件的定义,特点和分类 软件的定义 软件的特点 软件的分类 软件危机的定义和表现形式 软件危机 表现形式 软件危机的产生原因及解决途径 产生软件危机的原因 软件工程 概念 软件工程的研究内容和基本原理 内容 软件工程的基本原理 软件过程…...
SpringBoot_02
Web后端开发_07 SpringBoot_02 SpringBoot原理 1.配置优先级 1.1配置 SpringBoot中支持三种格式的配置文件: application.propertiesapplication.ymlapplication.yaml properties、yaml、yml三种配置文件,优先级最高的是properties 配置文件优先级…...

实验报告-实验四(时序系统实验)
软件模拟电路图 说明 SW:开关,共六个Q1~Q3:输出Y0~Y3:输出 74LS194 首先,要给S1和S0高电位,将A~D的数据存入寄存器中(如果开始没有存入数据,那么就是0000在里面移位,不…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
