C++ day56 两个字符串的删除操作 编辑距离
题目1:583 两个字符串的删除操作
题目链接:两个字符串的删除操作
对题目的理解
返回使两个单词word1和word2相同的最少删除多少个元素,两个单词至少包含一个字母,且仅包含小写字母
思路1:这道题与昨天的不同子序列很相似,只是有一点不同,不同子序列是使用s字符串去匹配t字符串,而本题可以对word1进行删减得到word2,也可以用word2删减获得word1,经过一系列删除操作,最终两个单词相等就可以了。
思路2:本题其实就是求word1和word2达到最长公共子序列时,使用两个单词的长度之和减去最长公共子序列的长度的2倍。
动态规划(思路1)
动规五部曲
1)dp数组及下标i的含义
dp[i][j]:以i-1结尾的word1和以j-1结尾的word2达到word1和word2相同的最少操作次数
2)递推公式
还是考虑两种情况,当前子串word1结尾的字符与子串word2结尾的字符相等和不等的情况
i)结尾的字符相等,即word1[i-1]==word2[j-1],因为已经相等了,这两个字符就不会改变操作的次数,那么此时就不用考虑这两个字符了,(模拟将这两个字符删除),则当前的结果与这两个字符的前面的字符结尾(word1[i-1],word2[j-1])的结果相同,即dp[i][j] = dp[i-1][j-1]
ii)结尾的字符不等,因为word1[i-1]和word2[j-1]两个字符不等,所以考虑删除元素,这又可以分为3种情况,
删除word1[i-1] ,也就是不考虑word1[i-1]这个元素了,那么在word1中没有这个元素了,则最终的结果应该是其前一个字符word1[i-2]与word2[j-1]进行比较,看是否相等,
即 dp[i][j]=dp[i-1][j]+1,因为删除一个元素,所以加1
删除word2[j-1] ,不考虑word2[j-1]这个元素了,那么在word2中就没有这个元素了,则最终的结果应该是word2子串的前一个字符word2[j-2]与word1[i-1]进行比较,看是否相等,
即dp[i][j]=dp[i][j-1],因为删除了一个元素,所以加1
删除word1[i-1]和word2[j-1],不考虑word1[i-1]和word2[j-1]这两个元素了,那么在word1和word2中就没有这两个元素了,最终就是word2子串的前一个字符word2[i-2]与word1子串的前一个字符word1[i-2]进行比较 ,即 dp[i][j]=dp[i-1][j-1]+2,因为删除了2个元素,所以加2
dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+2)
3)dp数组初始化

根据递推公式,第一行,第一列都要进行初始化,即dp[i][0] dp[0][j]都需要进行初始化
根据dp数组定义 dp[i][0]代表以i-1结尾的word1和以-1结尾的word2相同的最小操作次数,word2以-1结尾,说明word2是空串,那么要想达到两个子串相等,说明word1需要删除i个元素,需要最少操作i次,所以dp[i][0]=i
同理,dp[0][j]代表以-1结尾的word1和以j-1结尾的word2相同的最小操作次数,word1是空串,此时要想让两个子串相等,word1也需要变为空串,需要将word2中的元素全部删除才可以,即删除j个元素,最少操作j次 ,所以dp[0][j]=j
4)遍历顺序
根据递推公式,从左到右遍历,从上到下遍历
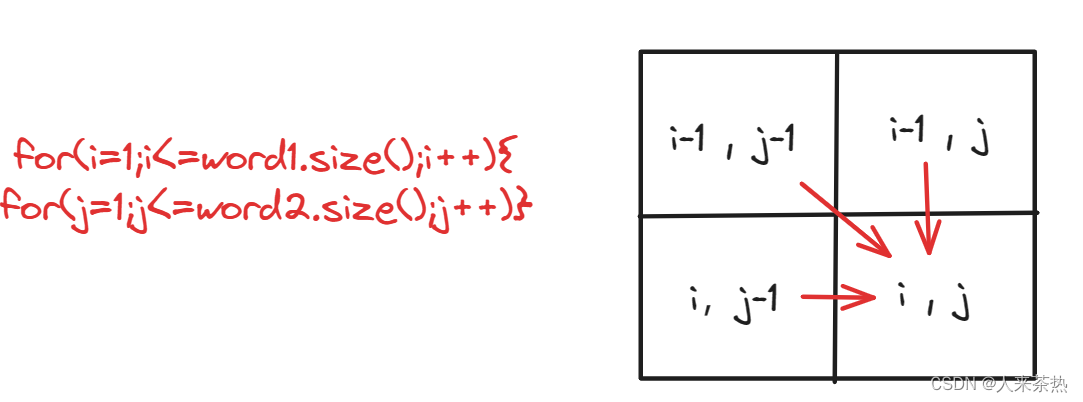
5)打印dp数组
代码,注意定义dp数组的时候,一定要word1.size()+1,一定要加1,因为dp数组的定义是以i-1结尾,最终要遍历到最后一个元素word1.size()-1的时候,才是dp数组的最后一个元素word1.size()减去1为结尾
class Solution {
public:int minDistance(string word1, string word2) {//定义dp数组vector<vector<int>> dp(word1.size()+1,vector<int>(word2.size()+1));//初始化dp数组for(int i=0;i<word1.size();i++) dp[i][0]=i;for(int j=0;j<word2.size();j++) dp[0][j]=j;for(int i=1;i<=word1.size();i++){for(int j=1;j<=word2.size();j++){if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1];else dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+2));}}return dp[word1.size()][word2.size()];}
};上面的代码会出现如下错误

根据出现的错误,将其对应的各个dp数组打印出来,发现dp[0][1]以及dp[1][0]仍是0,并没有初始化成1,所以初始化这里出现了问题

就是因为在初始化的时候,没有将dp[word1.size()][0]和dp[0][word2.size()]初始化
注意初始化数组时,因为是初始化整个dp[i][j],所以将dp[i][0]和dp[0][j]整个进行初始化,所以,i从0到word1.size()都要初始化 ,j从0到word2.size()都要初始化,注意初始化时,一定要使得i<=word1.size(),j<=word2.size(),等号不能丢掉,否则就会在案例出现的时候出现错误
因此,将代码修改如下:
class Solution {
public:int minDistance(string word1, string word2) {//定义dp数组vector<vector<int>> dp(word1.size()+1,vector<int>(word2.size()+1));//初始化dp数组for(int i=0;i<=word1.size();i++) dp[i][0]=i;for(int j=0;j<=word2.size();j++) dp[0][j]=j;for(int i=1;i<=word1.size();i++){for(int j=1;j<=word2.size();j++){if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1];else dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+2));}}return dp[word1.size()][word2.size()];}
};- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
流程图
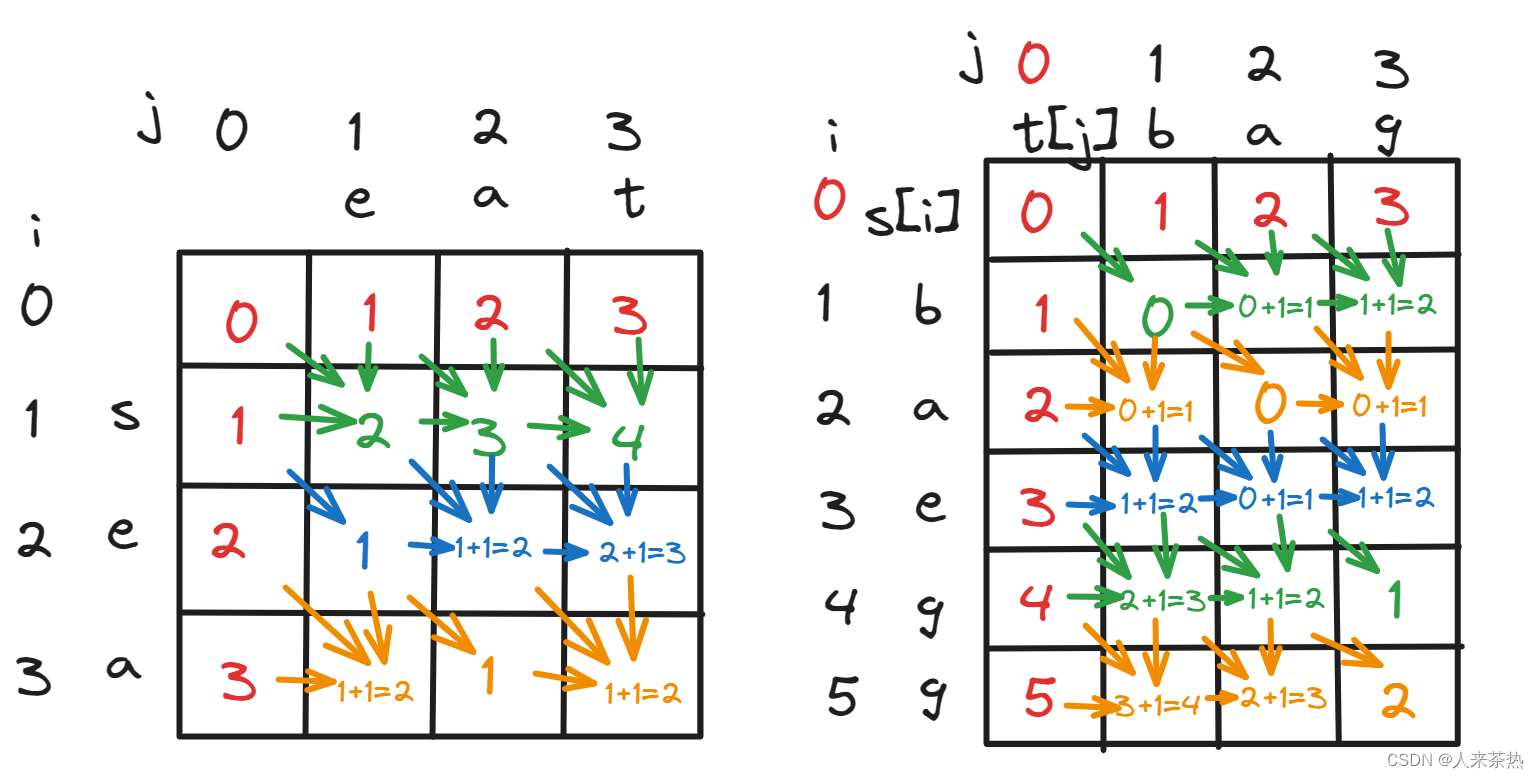
动态规划(思路2)
思路2:本题也可以在求最长公共子序列的基础上进行求解,将word1和word2的最长公共子序列的长度求出来,然后使用word1和word2的长度之和减去2倍的公共子序列的长度,即为所求。
流程
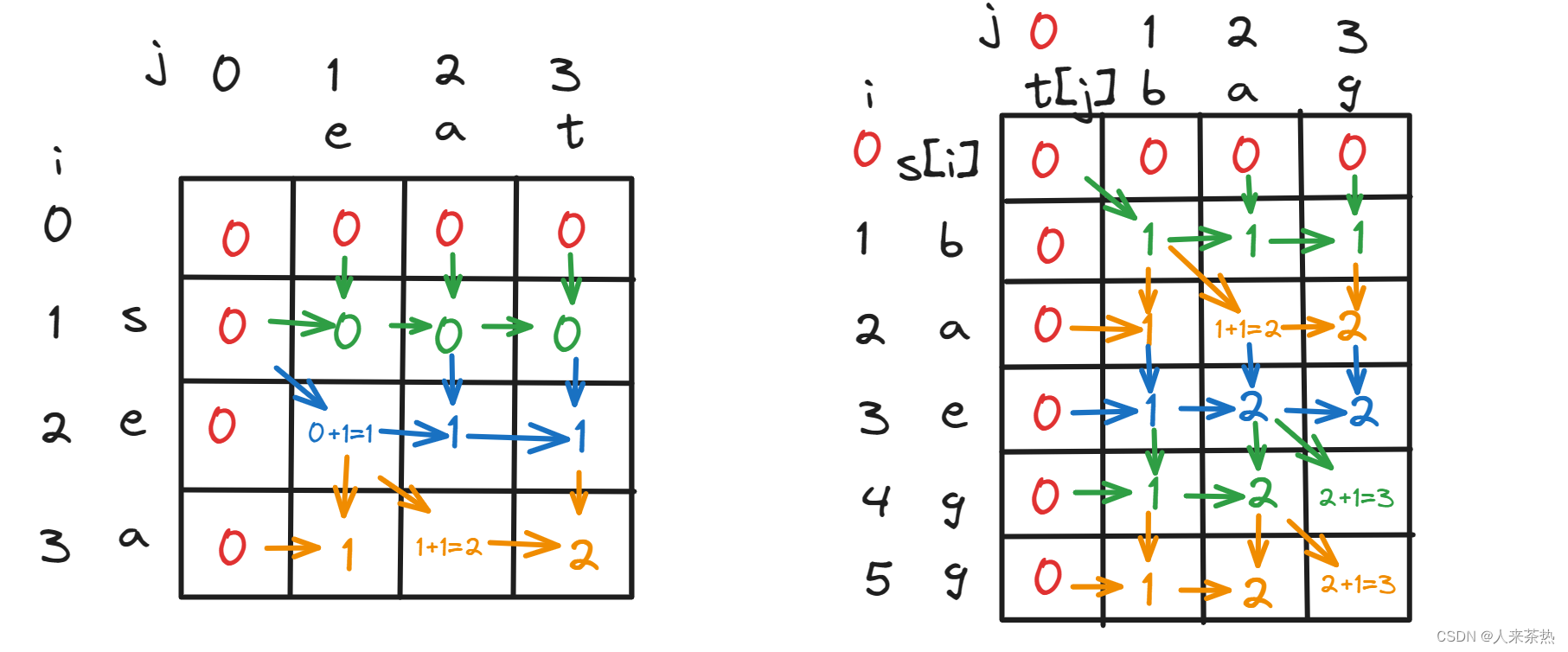
代码
class Solution {
public:int minDistance(string word1, string word2) {//定义并初始化dp数组vector<vector<int>> dp(word1.size()+1,vector<int>(word2.size()+1,0));for(int i=1;i<=word1.size();i++){for(int j=1;j<=word2.size();j++){if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]); }}int result = word1.size()+word2.size()-2*dp[word1.size()][word2.size()];return result;}
};- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
题目2:72 编辑距离
题目链接:编辑距离
对题目的理解
返回将单词word1转换成word2使用最少的操作数,两个单词的长度大于等于0,且均由小写字母组成,操作包括插入一个字符,删除一个字符以及替换一个字符
动态规划
动规五部曲
1)dp数组及下标i的定义
dp[i][j]:以下标i-1结尾的word1和以下标j-1结尾的word2相同的最少操作次数
2)递推公式
还是分为两种情况,两个元素相等以及两个元素不等的情况
1)两个元素word1[i-1]和word2[j-1]相等,则不考虑这两个元素,因为已经相等了,所以不需要对二者进行操作,只需要考虑前面的word1[i-2]和word2[j-2]就行,dp[i][j]=dp[i-1][j-1]
2)两个元素word1[i-1]和word2[j-1]不相等,则需要对元素进行删减以及替换的操作,所以这又可以分为3种情况
i)只考虑word1[i-1],只对这个元素进行操作,当word1[i-1]不等于word2[j-1]时,将word1[i-1]删除,那么此时对于word1而言,就是以word1[i-2]为结尾的子串与word2[j-1]为结尾的子串的最小操作次数的基础上进行操作(删除)加1,因此,dp[i][j]=dp[i-1][j]+1 加1是因为进行了一个删除操作
ii)只考虑word2[j-1],只对这个元素进行操作,当word1[i-1]不等于word2[j-1]时,将word2[j-1]删除,那么对于word2而言,只剩下以word2[j-2]为结尾的子串与word1[i-1]为结尾的子串的最小操作次数的基础上进行操作(删除)加1,dp[i][j]=dp[i][j-1]+1 加1是因为进行了一个删除操作
注:word2添加一个元素,相当于word1删除一个元素,例如 word1 = "ad" ,word2 = "a",word1删除元素'd' 和 word2添加一个元素'd',变成word1="a", word2="ad", 最终的操作数是一样!
iii)如果word1[i-1]不等于word2[j-1],要使得这两个位置对应的元素相等(dp[i][j]=dp[i-1][j-1],这个等式是word[i-1]和word[j-1]相等的情况,但是此时是要让这两个元素相等,所以需要考虑这两个元素在原来以word1[i-2]为结尾的子串和以word2[j-2]为结尾的子串相同进行操作的基础上加上一个替换的操作就ok),只需要dp[i][j]=dp[i-1][j-1]+1 加1是因为进行了一次替换操作
dp[i][j]= min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+1)
3)dp数组初始化
根据递推公式,第一行和第一列需要初始化,
根据dp数组的定义,dp[i][0]表示以下标i-1为结尾的word1和以下标-1为结尾的word2相同的最少操作次数,而以下标-1为结尾的word2是一个空串,要想使得这两个串的长度相等,那么word1至少需要操作i次,因为word1中含有i个元素
dp[0][j]表示以下标-1为结尾的word1和以下标j-1为结尾的word2相同的最少操作次数,而以下标01结尾的word1是一个空串,要想使得word1和word2的长度相等,那么word2至少需要操作j次,因为word2中含有j个元素
因此初始化如下
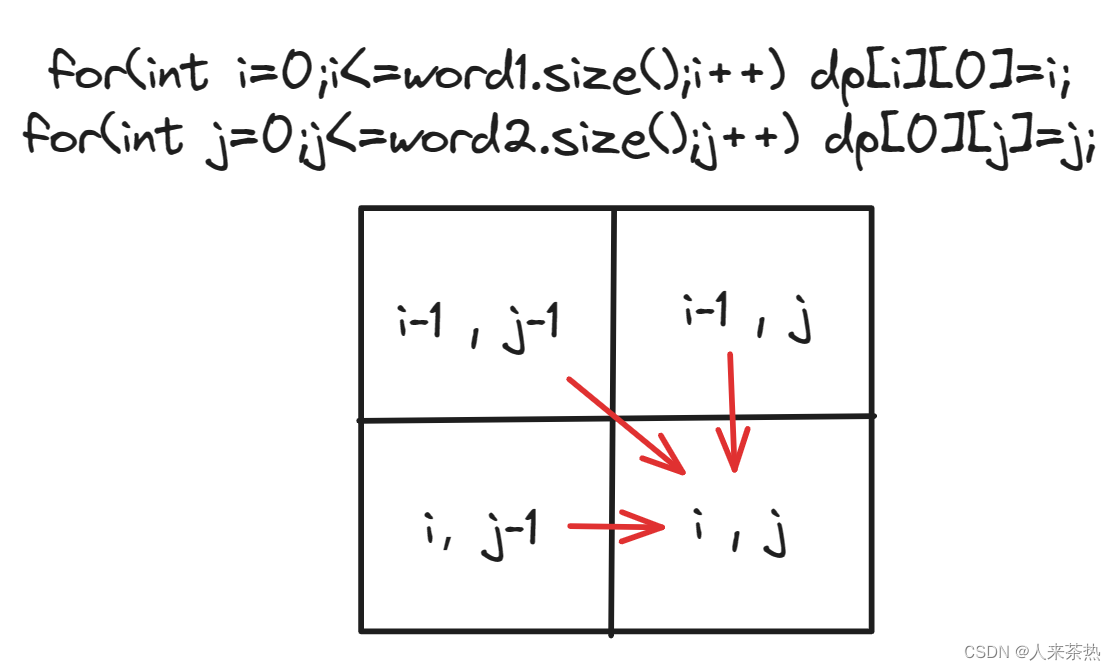
注意for循环中一定要是小于等于,一定要有等于,这样才能确保dp数组中的最后一个边界值,即dp[word1.size()][0]和dp[0][word2.size()]初始化了,如果只写小于的话,这组元素就会被落掉,相当于dp[word1.size()][0]和dp[0][word2.size()]没有进行初始化,默认为0
4)遍历顺序
根据递推公式,从左往右遍历,从上到下遍历
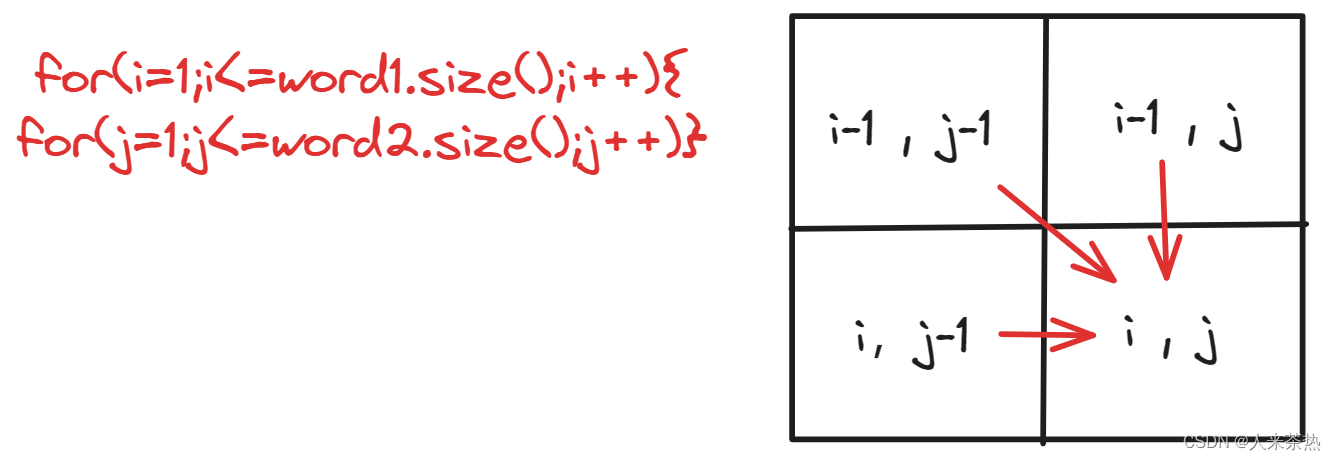
5)打印dp数组
最终的结果在dp[word1.size()][word2.size()]中
代码
class Solution {
public:int minDistance(string word1, string word2) {//定义dp数组vector<vector<int>> dp(word1.size()+1,vector<int>(word2.size()+1));//初始化dp数组for(int i=0;i<=word1.size();i++) dp[i][0]=i;for(int j=0;j<=word2.size();j++) dp[0][j]=j;for(int i=1;i<=word1.size();i++){for(int j=1;j<=word2.size();j++){if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1];else dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+1));}}return dp[word1.size()][word2.size()];}
};- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
代码流程
删减元素
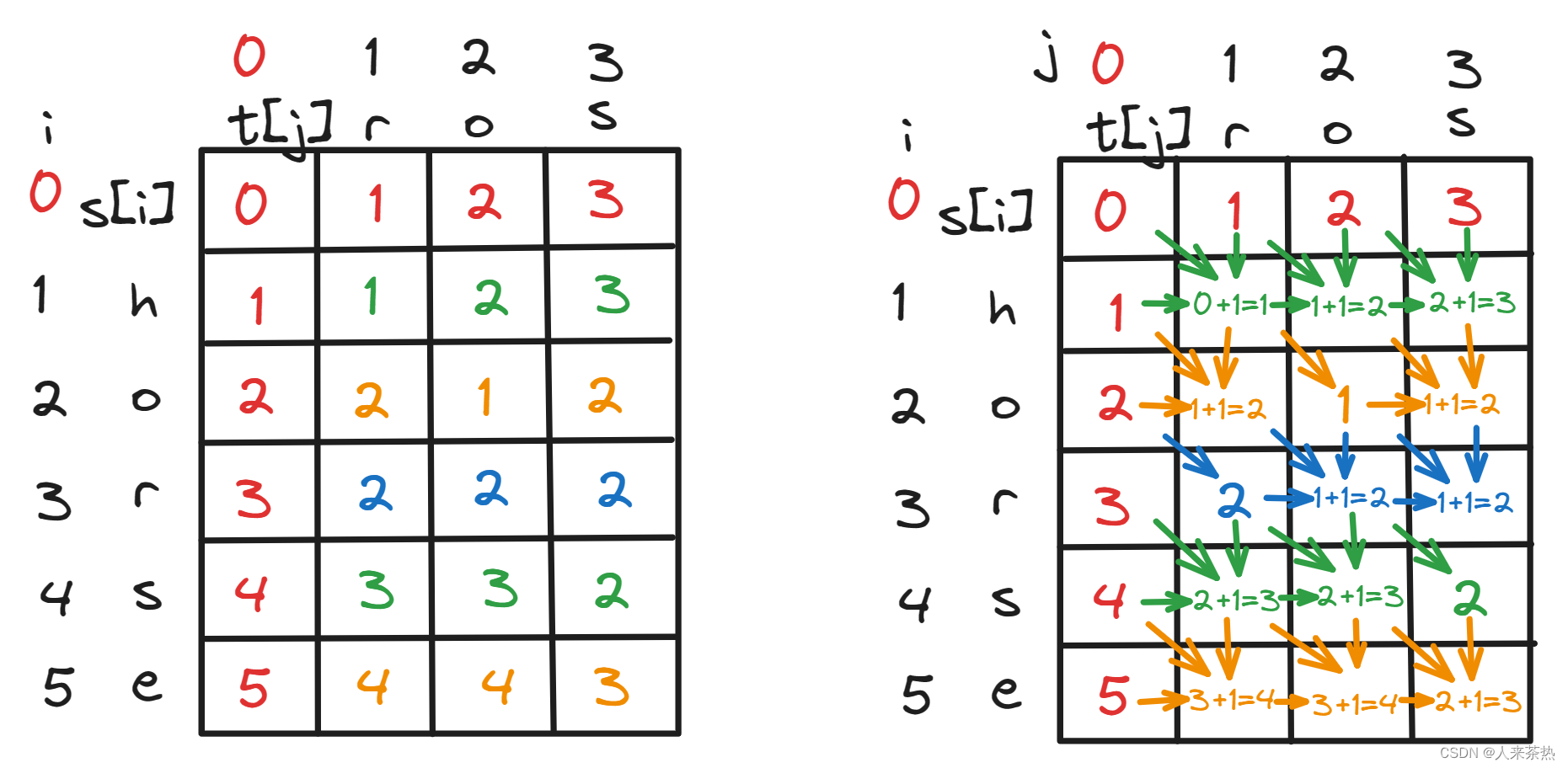
添加元素
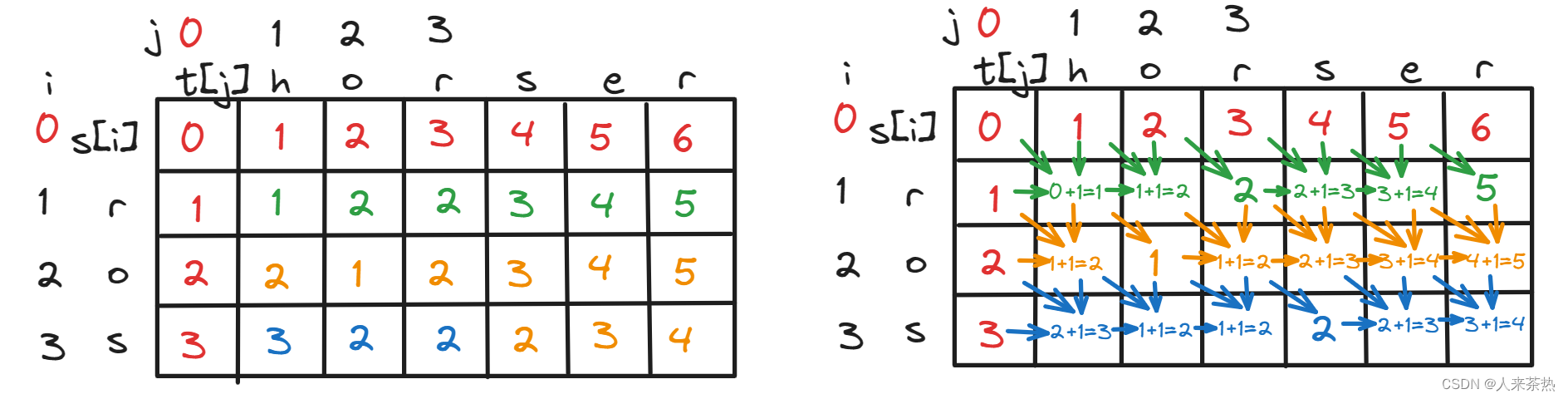
相关文章:

C++ day56 两个字符串的删除操作 编辑距离
题目1:583 两个字符串的删除操作 题目链接:两个字符串的删除操作 对题目的理解 返回使两个单词word1和word2相同的最少删除多少个元素,两个单词至少包含一个字母,且仅包含小写字母 思路1:这道题与昨天的不同子序列…...
Android studio中如何生成jar包?
文章目录 需求背景目录结构gradle结构makeJar的语法解析 执行makeJar 任务拿到jar包 需求背景 别部门做C语言开发的同学开发了一个库,需要给我们Android端去调用。 我们拿到源码,首先需要做的是通过CMake去把C源码编译链接成动态库。 当然静态库也行&am…...

【2】基于多设计模式下的同步异步日志系统-设计模式
6. 相关技术知识补充 6.1 不定参函数 在初学C语⾔的时候,我们都⽤过printf函数进⾏打印。其中printf函数就是⼀个不定参函数,在函数内部可以根据格式化字符串中格式化字符分别获取不同的参数进⾏数据的格式化。 ⽽这种不定参函数在实际的使⽤中也⾮常…...
第十五届蓝桥杯模拟赛B组(第二期)C++
前言: 第一次做蓝桥模拟赛的博客记录,可能有很多不足的地方,现在将第十五届蓝桥杯模拟赛B组(第二期)的题目与代码与大家进行分享,我是用C做的,有好几道算法题当时自己做的也是一脸懵,…...
企业ERP软件定制开发要注意|app小程序搭建
企业ERP软件定制开发要注意|app小程序搭建 企业ERP软件定制开发是一项复杂而且关键的任务,它需要深入理解企业的需求和流程,并且以此为基础进行设计和开发。以下是一些关于企业ERP软件定制开发的注意事项。 首先,我们必须确保在进行定制开发之…...

系统架构设计-权限模块的设计
系统架构-权限模块的设计 如何评估一个研发人员技术水平,在大部分的情况下不是看其完成业务代码的好坏,更多的时候还是需要看这个研发人员从零构建一个完整项目的能力,在大公司中这样的机会可能相对较少,大部分的时间里都是对现有…...
IDEA切换Python虚拟环境
前言 因为之前一直使用的IDEA开发,换到VSCODE之后各种不习惯,特别是DEBUG的操作,特别难受,因此决心换回IDEA 环境配置 已有项目调整 进入Project 选择SDKs,新建Python 配置Conda以及虚拟环境 有就选择一个虚拟环境…...

《opencv实用探索·十一》opencv之Prewitt算子边缘检测,Roberts算子边缘检测和Sobel算子边缘检测
1、前言 边缘检测: 图像边缘检测是指在图像中寻找灰度、颜色、纹理等变化比较剧烈的区域,它们可能代表着物体之间的边界或物体内部的特征。边缘检测是图像处理中的一项基本操作,可以用于人脸识别、物体识别、图像分割等多个领域。 边缘检测…...
prime靶机打靶记录
靶机下载地址 https://download.vulnhub.com/prime/Prime_Series_Level-1.rar nmap搜索目标 使用nmap -sn 192.168.41.0/24找到目标靶机192.168.41.136 扫描端口,因为是靶机,所以速率直接调了10000 扫出来两个端口22和80,进行详细的扫描 没…...

树莓派,linux换清华源
清华源网址 https://mirrors.tuna.tsinghua.edu.cn/help/raspbian/ 更换软件源 鉴于国内网络环境下载各大镜像,软件包速度慢的问题,需要更换软件源,以防下载慢,且在本教程中,统一更换为清华源。 2.3.1 更换树莓派软…...
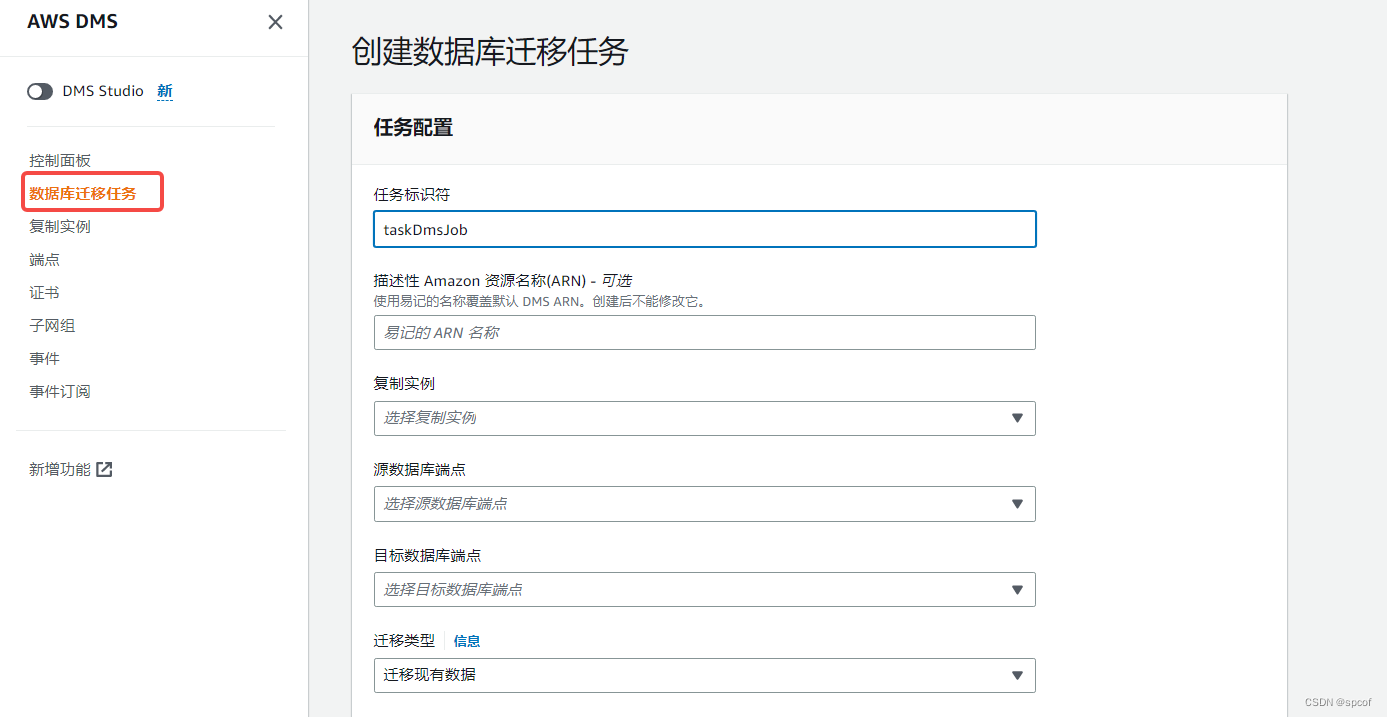
公有云迁移研究——AWS DMS
大纲 1 什么是DMS2 DMS的作用3 DMS在迁移的时候都做些什么4 在使用DMS的时候我们需要做些什么5 操作5.1 创建两个数据库终端节点5.2 创建迁移任务 6 可能遇到的问题7 总结 在本地机房或其他云往AWS上做迁移时,往往会遇到数据库迁移的任务。如果数据量不是特别大&…...

一起学docker系列之十七Docker Compose 与手动操作的比较与优势分析
目录 1 前言2 不使用 Docker Compose2.1 启动 MySQL 容器2.2 启动 Redis 容器2.3 启动微服务容器 3 使用 Docker Compose4 使用 Docker Compose 的优势5 结语参考地址 1 前言 在当今容器化应用的开发与部署中,容器编排工具的选择对于简化流程、提高效率至关重要。本…...

IP地址定位不准确的情况研究
在互联网的浩瀚海洋中,每一台连接到网络的设备都被赋予了一个独特的标识符,这就是IP地址。它就像是我们在线身份的一部分,帮助我们与他人进行通信,获取信息,以及享受各种网络服务。然而,由于各种原因&#…...
武汉凯迪正大KDZD5289硫化曲线测试仪(电脑无转子硫化仪)
电脑无转子硫化仪 硫化时间测试仪 硫化曲线仪 硫化曲线测试仪 武汉凯迪正大KDZD5289产品概述 KDZD5289硫化曲线测试仪(电脑无转子硫化仪)采用电脑控制进口温控仪进行准确控温,计算机适时进行数据处理并可进行统计、分析、存储对比等ÿ…...

Topic和Partition
作用 主题作为消息的一级分类, 分区是对二级分类。分区是Kafka可伸缩性和水平扩展的关键, 也是多副本机制保证可用性的基础。分区可以有一到多个副本, 每个副本对应1个日志文件, 每个日志文件对应1到多个日志分段。每个日志分段又可以细分为日志文件, 索引文件和快照文件。 创…...

算法通关村第十四关|黄金挑战|数据流的中位数
数据流的中位数 原题:力扣295. 设计一种数据结构可以支持添加整数和返回中位数的操作。 之前写过找中间用两个堆,这道题就可以使用一个大顶堆和一个小顶堆。 大顶堆存储比较小的元素,小顶堆存储比较大的元素。 class MedianFinder {Prio…...
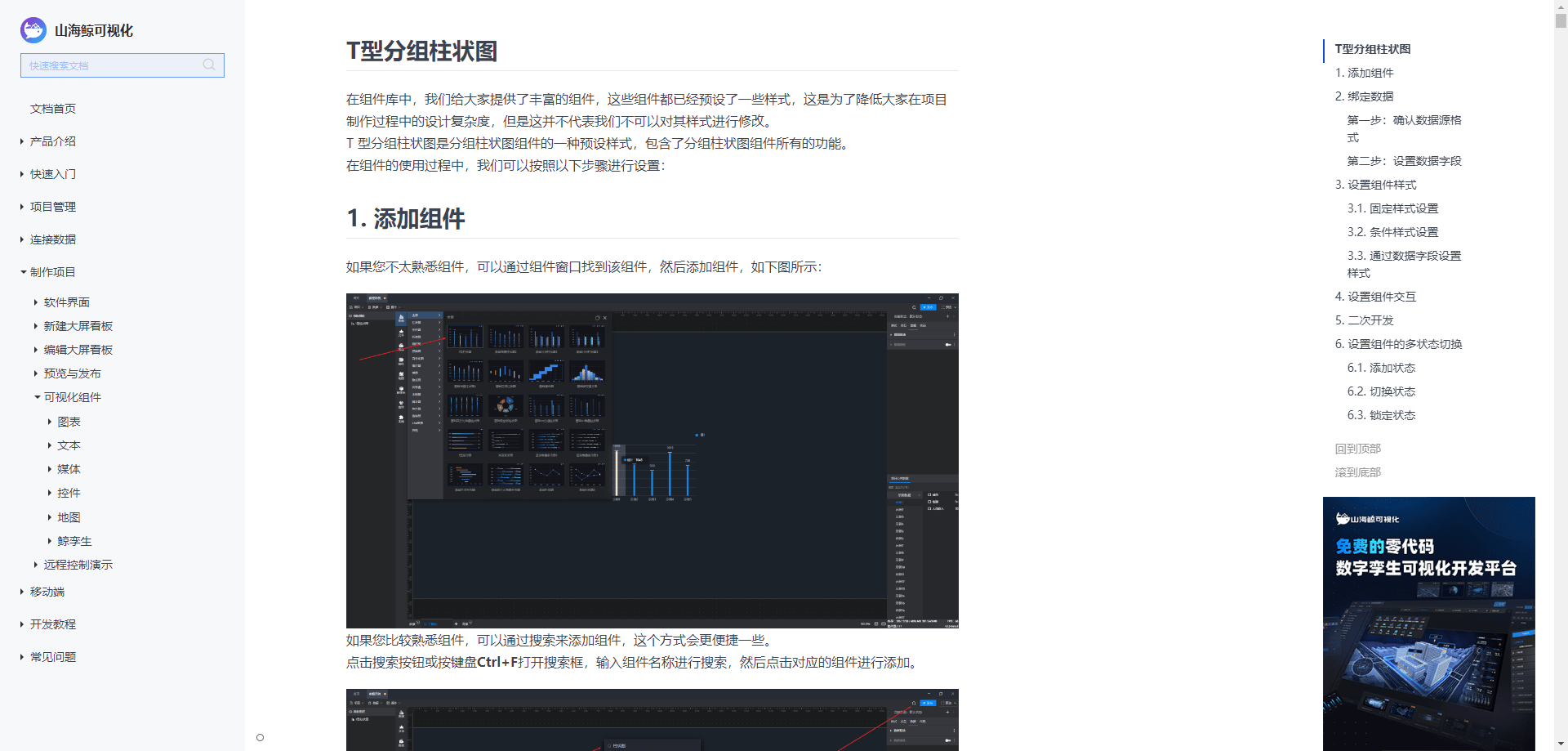
挑选数据可视化工具:图表类型、交互功能与数据安全
作为一名数据分析师,我经常需要使用各种数据可视化工具来将数据以直观、清晰的方式呈现出来,以便更好地理解和分析。在市面上的众多可视化工具中,我根据实际需求和项目特点进行选择。本文将从以下几个角度对市面上的数据可视化工具进行对比&a…...

华纳云:有效解决服务器宕机的办法
服务器宕机可能是由多种原因引起的,包括硬件故障、软件问题、网络问题等。以下是一些简单的解决服务器宕机问题的办法: 检查硬件连接: 确保服务器的所有硬件连接正常。检查电源线、网络连接、存储设备连接等,确保没有松动或断开的…...

坦克大战-部分
通过键盘操控坦克移动,转弯,射击 消灭所有敌人可以过关 23个类,3个gif图片 wsad控制移动 j射击 砖墙限制移动,可以打穿;铁墙,限制移动,不能打穿;水&#x…...

OracleRac跨网段修改Public IP/VIP/Private IP/Scan IP
本验证于测试环境,生产操作需谨慎 现为测试环境,机器有且仅有两个网卡存在,需求修改Public IP/VIP/Private IP/Scan IP,把Public IP/VIP/Scan IP的网段改为Private IP的网段,Private IP于Public IP网段互换。 先停掉两…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...
