代码随想Day24 | 回溯法模板、77. 组合
理论基础
回溯法和递归不可分割,回溯法是一种穷举的方法,通常需要剪枝来降低复杂度。回溯法有一个选择并退回的过程,可以抽象为树结构,回溯法的模板如下:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}77. 组合
这道题是回溯的经典题目,按照递归三步走:
参数:
在这里要定义两个全局变量,一个用来存放符合条件单一结果,一个用来存放符合条件结果的集合。函数里一定有两个参数,既然是集合n里面取k个数,那么n和k是两个int型的参数。
然后还需要一个参数,为int型变量startIndex,这个参数用来记录本层递归的中,集合从哪里开始遍历(集合就是[1,...,n] )。
回溯函数结束条件:
path这个数组的大小如果达到k,说明我们找到了一个子集大小为k的组合了,此时用result二维数组,把path保存起来,并终止本层递归。
单层搜索的过程
回溯法的搜索过程就是一个树型结构的遍历过程,在如下图中,可以看出for循环用来横向遍历,递归的过程是纵向遍历。

如此我们才遍历完图中的这棵树。for循环每次从startIndex开始遍历,然后用path保存取到的节点i。可以看出backtracking(递归函数)通过不断调用自己一直往深处遍历,总会遇到叶子节点,遇到了叶子节点就要返回。backtracking的下面部分就是回溯的操作了,撤销本次处理的结果。
此外:比较重要的剪枝部分:
可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。
如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了。注意代码中i,就是for循环里选择的起始位置。
for (int i = startIndex; i <= n; i++) {
优化过程如下:
-
已经选择的元素个数:path.size();
-
还需要的元素个数为: k - path.size();
-
在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
最终详细代码如下:
class Solution
{
public:vector<int> path;vector<vector<int>> res;void backTracking(int n, int k, int startindex) {//endif (path.size() == k) {res.push_back(path);return;}// backtrackingfor (int i = startindex; i <= n - (k - path.size()) + 1; i++) {path.push_back(i);backTracking(n, k, i + 1);path.pop_back();}}vector<vector<int>> combine(int n, int k) {backTracking(n, k, 1);return res;}
};相关文章:

代码随想Day24 | 回溯法模板、77. 组合
理论基础 回溯法和递归不可分割,回溯法是一种穷举的方法,通常需要剪枝来降低复杂度。回溯法有一个选择并退回的过程,可以抽象为树结构,回溯法的模板如下: void backtracking(参数) {if (终止条件) {存放结果;return;}…...

搜索与回溯算法②
求0-9的数字可以组成的所有k 位数。 def backtrack(start, path, k, n, results):"""核心函数。:param start: 下一个添加的数字的起始位置:param path: 当前构建的路径,代表一个组合:param k: 组合中所需的数字个数:param n: 可选数字的最大值:par…...
Centos图形化界面封装OpenStack Ubuntu镜像
目录 背景 环境 搭建kvm环境 安装ubuntu虚机 虚机设置 系统安装 登录虚机 安装cloud-init 安装cloud-utils-growpart 关闭实例 删除细节信息 删除网卡细节 使虚机脱离libvirt纳管 结束与验证 压缩与转移 验证是否能够正常运行 背景 一般的镜像文件在上传OpenSt…...

使用Jmeter进行http接口测试怎么做?
前言: 本文主要针对http接口进行测试,使用Jmeter工具实现。 Jmter工具设计之初是用于做性能测试的,它在实现对各种接口的调用方面已经做的比较成熟,因此,本次直接使用Jmeter工具来完成对Http接口的测试。 一、开发接…...

创建腾讯云存储桶---上传图片--使用cos-sdk完成上传
创建腾讯云存储桶—上传图片 注册腾讯云账号https://cloud.tencent.com/login 登录成功,选择右边的控制台 点击云产品,选择对象存储 创建存储桶 填写名称,选择公有读,私有写一直下一步,到创建 选择安全管理&#…...
12.3_黑马MybatisPlus笔记(上)
目录 02 03 04 05 06 07 编辑 thinking:system.out::println?编辑 thinking:list.of? 08 thinking:RequestParam和 ApiParam注解使用? thinking:RequestParam 和PathVariable的区别? 编辑 编…...

智能优化算法应用:基于寄生捕食算法无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于寄生捕食算法无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于寄生捕食算法无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.寄生捕食算法4.实验参数设定5.算法结果6.参考…...

全息图着色器插件:Hologram Shaders Pro for URP, HDRP Built-in
8个新的Unity全息图着色器,具有故障效果,扫描线,网格线,和更多其他效果!与所有渲染管线兼容。 软件包添加了一系列的全息图着色器到Unity。从基本的全息图与菲涅耳亮点,先进的全息图与两种故障效应,扫描线,文体点阵和网格线全息图! 特色全息效果 Basic-支持菲涅耳发光照…...

Python Opencv实践 - 简单的AR项目
这个简单的AR项目效果是,通过给定一张静态图片作为要视频中要替换的目标物品,当在视频中检测到图片中的物体时,通过单应矩阵做投影,将视频中的物体替换成一段视频播放。这个项目的所有素材来自自己的手机拍的视频。 静态图片&…...

Java不可变集合
Java不可变集合 不可变集合:也就是不可以被修改的集合 创建不可变集合的应用场景 ●如果某个数据不能被修改,把它防御性地拷贝到不可变集合中是个很好的实践。 ●当集合对象被不可信的库调用时,不可变形式是安全的。 简单理解࿱…...

openGauss学习笔记-146 openGauss 数据库运维-备份与恢复-配置文件的备份与恢复
文章目录 openGauss学习笔记-146 openGauss 数据库运维-备份与恢复-配置文件的备份与恢复146.1 背景信息146.2 前置条件146.3 操作步骤146.4 示例 openGauss学习笔记-146 openGauss 数据库运维-备份与恢复-配置文件的备份与恢复 146.1 背景信息 在openGauss使用过程中&#x…...

一文读懂中间件
前言:在程序猿的日常工作中, 经常会提到中间件,然而大家对中间件的理解并不一致,导致了一些不必要的分歧和误解。“中间件”一词被用来描述各种各样的软件产品,在不同文献中有着许多不同的中间件定义,包括操…...

【编程基础心法】「设计模式系列」让我们一起来学编程界的“兵法”设计模式(序章)
一起来学编程界的“兵法”设计模式(序章) 设计模式是什么设计模式的概念设计模式的分类创建型模式(5种)结构型模式(7种)行为型模式(11种) 设计模式应用场景工厂模式的实现及应用单例…...

技术阅读周刊第第8️⃣期
技术阅读周刊,每周更新。 历史更新 20231103:第四期20231107:第五期20231117:第六期20231124:第七期 Prometheus vs. VictoriaMetrics (VM) | Last9 URL: https://last9.io/blog/prometheus-vs-victoriametrics/?refd…...

HTML程序大全(2):通用注册模版
一、正常情况效果 二、某项没有填写的效果 三、没有勾选同意项的效果 四、代码 <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title>注册</title><style>body {font-family: Arial, sans-serif;background-color…...

【循环结构 for、break、continue高级用法】
在 C++ 中,for 循环是一种常用的循环结构,它用于重复执行代码块直到满足指定的条件。for 循环的基础用法相对简单,而高级用法则涉及更复杂的控制结构和技术。让我们探讨这些用法,并通过一些示例来加深理解。 文章目录 基础用法高级用法实战示例注意事项结合 break 和 conti…...
JAVA网络编程——BIO、NIO、AIO深度解析
I/O 一直是很多Java同学难以理解的一个知识点,这篇帖子将会从底层原理上带你理解I/O,让你看清I/O相关问题的本质。 1、I/O的概念 I/O 的全称是Input/Output。虽常谈及I/O,但想必你也一时不能给出一个完整的定义。搜索了谷哥欠,发…...

Linux高级系统编程-3 进程
概念 进程与程序的区别 程序:一个可执行文件, 占磁盘空间,是静态的 进程:一个程序运行的过程, 占内存,动态的。 单道程序和多道程序 单道程序设计: 所有进程一个一个排队执行。若 A 阻塞, B 只能等待࿰…...
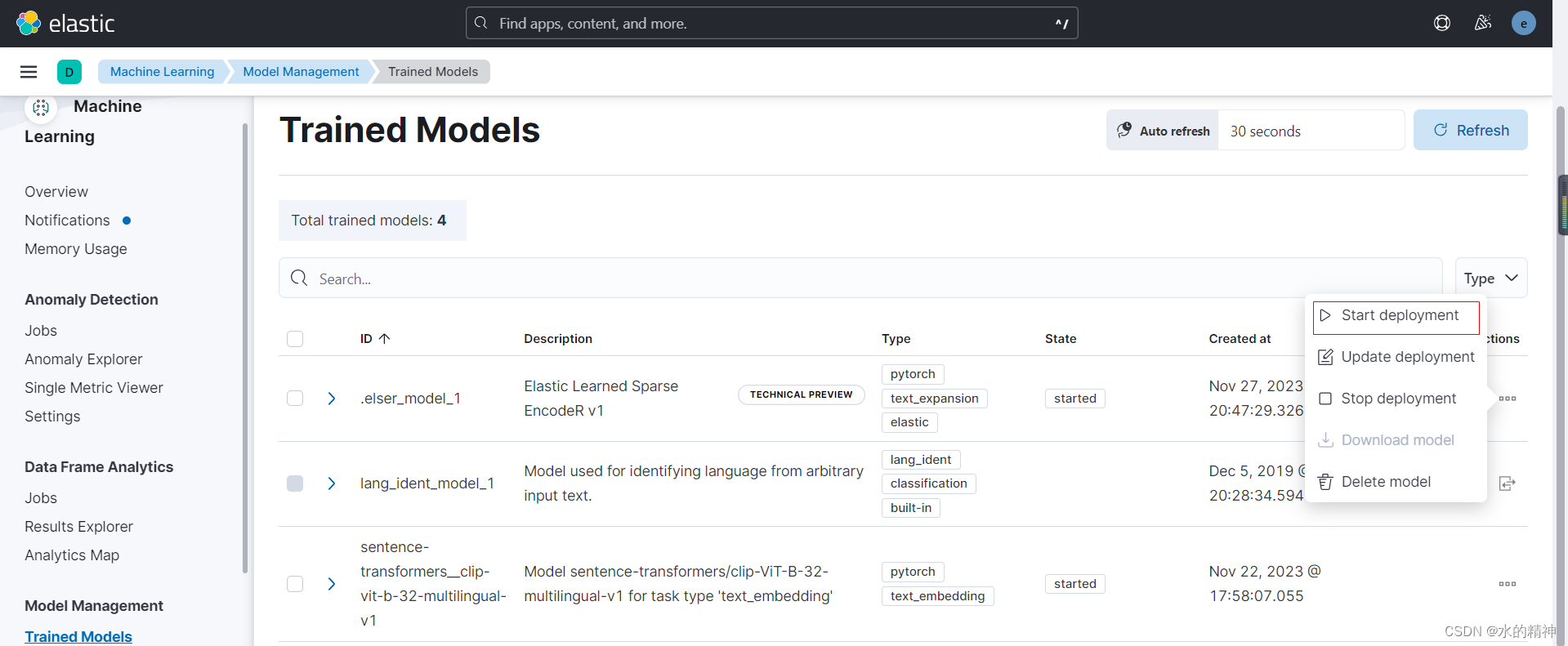
ES-ELSER 如何在内网中离线导入ES官方的稀疏向量模型(国内网络环境下操作方法)
ES官方训练了稀疏向量模型,用来支持语义检索。(目前该模型只支持英文) 最好是以离线的方式安装。在线的方式,在国内下载也麻烦,下载速度也慢。还不如用离线的方式。对于一般的生产环境,基本上也是网络隔离的…...

Excel 使用技巧
Excel 使用技巧 注意: excel 中设计计算的字符尽量使用英文。 拼接两段文字(字符串拼接) 方法一 在需要计算的单元格上,键入 点击 A1(点击需要拼接的单元格) & C1(点击需要拼接的单元格) 举例: 姓名栏想要拼接 姓 和 名 两列点击姓名这一…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
