代码随想录算法训练营第四十二天 _ 动态规划_01背包问题、416.分割等和子集。
学习目标:
动态规划五部曲:
① 确定dp[i]的含义
② 求递推公式
③ dp数组如何初始化
④ 确定遍历顺序
⑤ 打印递归数组 ---- 调试
引用自代码随想录!
60天训练营打卡计划!
学习内容:
二维数组处理01背包问题
- 听起来思路很简单,但其实一点也不好实现。
- 动态规划五步曲:
① 确定dp[i][j]的含义 : 任取[0, i]的物品后放进容量为j的背包 所能放的 最大价值
② 求递推公式 : dp[i][j] = max(dp[i-1][j] , dp[i-1][ j - weight[i] ] + value[i])
Ⅰ 不放物品 i : dp[i-1][j]
Ⅱ 放物品 i : dp[i-1][j - weight[i]] + value[i]
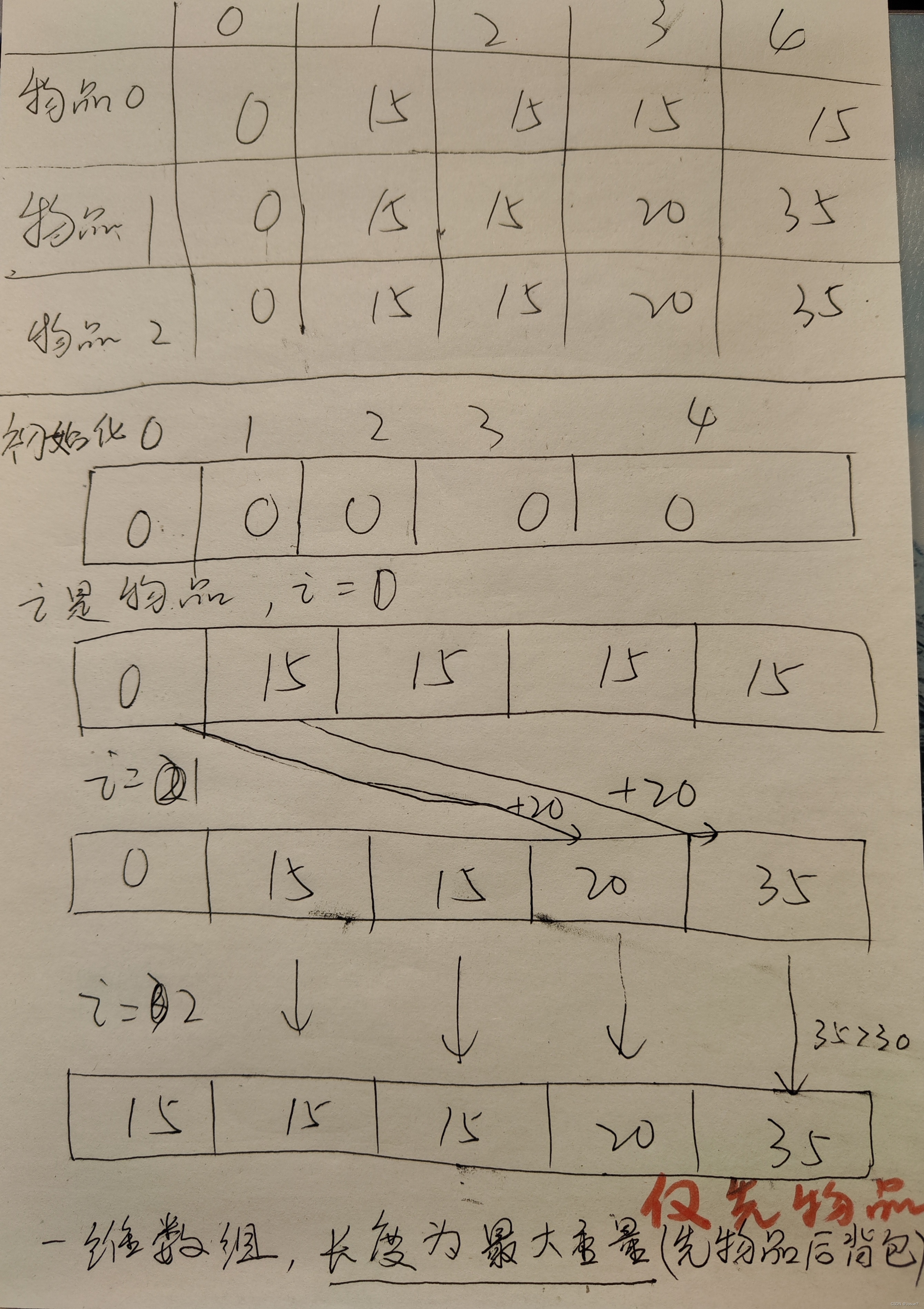
③ dp数组如何初始化 : 按下表的第一行和第一列赋值,其中箭头都是继承来的值,画圈的表示自己取得了最大值。
④ 确定遍历顺序 : 先物品后背包(行) / 先背包后物品(列)
import java.util.Scanner;public class Main {public static void main(String[] args) {//m,n分别代表物品种类和背包容量int itemSize = 0,bagSize = 0;Scanner sc = new Scanner(System.in);//获取itemSize和bagSize的值itemSize = sc.nextInt();bagSize = sc.nextInt();//初始化对应的重量数组和价值数组int[] weight = new int[itemSize];int[] value = new int[itemSize];//这两个都是物品的属性,大小只和物品数量有关for(int i = 0;i < itemSize;i++){weight[i] = sc.nextInt();}for (int i = 0;i < itemSize;i++){value[i] = sc.nextInt();}// int[] weight = {1,3,4};// int[] value = {15,20,30};// int bagSize = 4;testWeightBagProblem(weight,value,bagSize);}/*** 动态规划获得结果* @param weight 物品的重量* @param value 物品的价值* @param bagSize 背包的容量*/public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){int itemSize = weight.length;// dp数组的含义是:在[0,i]件物品中选择是否放入背包 的 最大价值int[][] dp = new int[itemSize][bagSize+1];// 初始化dp数组,默认都为0.// 只放一件物品时的初始化for(int j = weight[0]; j < bagSize+1; j++){dp[0][j] = value[0];}// 正常的为dp数组赋值,依赖左上位置的其他的dp值for(int i = 1; i < itemSize; i++){// j是背包容量for(int j = 1; j < bagSize+1; j++){// 如果容量不够放入新的物品,则从上一行继承if(j < weight[i]) dp[i][j] = dp[i-1][j];// 如果容量可以放入新的物品,则从上一行的左侧继承elsedp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i]);}}System.out.println(dp[itemSize-1][bagSize]);// 打印dp数组// for (int i = 0; i < goods; i++) {// for (int j = 0; j <= bagSize; j++) {// System.out.print(dp[i][j] + "\t");// }// System.out.println("\n");// }}
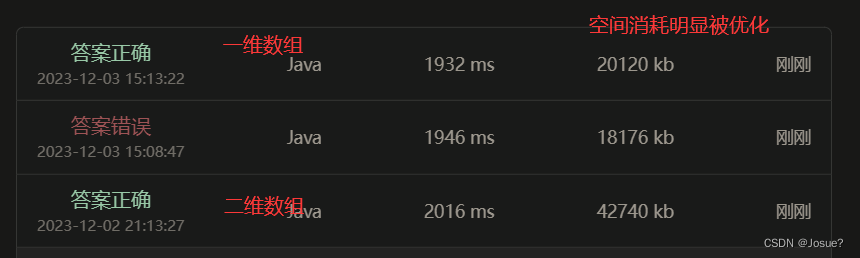
}一维数组处理01背包问题
- 动态规划五步曲:
① 确定dp[j]的含义 : 任取物品放进容量为j的背包 所能放的 最大价值
② 求递推公式 : dp[j] = max(dp[j] , dp[j - weight[i]] + value[i])
Ⅰ 不放物品 i : dp[j]
Ⅱ 放物品 i : dp[j - weight[i]] + value[i]
③ dp数组如何初始化 : 初始值全部附0,长度为容量的长度加1(j+1)
④ 确定遍历顺序 : 必须先物品后背包(行),且便利背包大小时,必须使用倒序的顺序遍历。(为了防止一个物品被使用多次,倒叙遍历时相同的物品仅能被取用一次)
import java.util.Scanner;public class Main {public static void main(String[] args) {//m,n分别代表物品种类和背包容量int itemSize = 0,bagSize = 0;Scanner sc = new Scanner(System.in);//获取itemSize和bagSize的值itemSize = sc.nextInt();bagSize = sc.nextInt();//初始化对应的重量数组和价值数组int[] weight = new int[itemSize];int[] value = new int[itemSize];//这两个都是物品的属性,大小只和物品数量有关for(int i = 0;i < itemSize;i++){weight[i] = sc.nextInt();}for (int i = 0;i < itemSize;i++){value[i] = sc.nextInt();}// int[] weight = {1,3,4};// int[] value = {15,20,30};// int bagSize = 4;testWeightBagProblem(weight,value,bagSize);}/*** 动态规划获得结果* @param weight 物品的重量* @param value 物品的价值* @param bagSize 背包的容量*/public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){// 创建dp一维数组int goods = weight.length; // 获取物品的数量int[] dp = new int[bagSize + 1];// 初始化dp数组// 创建数组后,其中默认的值就是0// 填充dp数组for (int i = 0; i < goods; i++) {// 必须使用倒叙遍历背包大小for (int j = bagSize; j > 0; j--) {// 防止越界错误if (j < weight[i]) {dp[j] = dp[j];} else {dp[j] = Math.max(dp[j] , dp[j-weight[i]] + value[i]);}}}System.out.print(dp[bagSize]);// 打印dp数组// System.out.print(dp[goods-1][bagSize] + "\n");// for (int i = 0; i < goods; i++) {// for (int j = 0; j <= bagSize; j++) {// System.out.print(dp[i][j] + "\t");// }// System.out.println("\n");// }}
}
416.分割等和子集
该题目可以等效为一个重量和价值相等的01背包问题,所以使用一维的数组就可。
- 因为题目问的是可不可以分为两个等和子集,没有问具体应该怎么分。
- 动态规划五步曲:
① 确定dp[j]的含义 : 容量为j的背包的最大价值
② 求递推公式 : dp[j] = max(dp[j], dp[j-nums[i]] + nums[i])
③ dp数组如何初始化 : 全部为零
④ 确定遍历顺序 : 先遍历物品,再倒叙遍历背包。 - 实现的特别巧妙,将该问题视为一个重量和价值相等的01背包问题,将目标和作为背包的重量,只要背包重量最大时能达到目标和的价值,即找到了一组数满足目标,那么此时该数组就可以分为等和的子集。
class Solution {public boolean canPartition(int[] nums) {int total = 0;for(int num :nums){total += num;}if(total % 2 == 1) return false;// target就是背包的最大重量int target = total / 2;int[] dp = new int[target+1];// 初始化:数组定义的时候已经被全部赋值0// 递推函数for(int i = 0; i < nums.length; i++){for(int j = target; j >= 0; j--){if(j < nums[i]) dp[j] = dp[j];else{dp[j] = Math.max(dp[j], dp[j - nums[i]]+nums[i]);}}}// 因为target是整除2得到的,所以只要能找到一组数使其和为target// 剩下的数的和也是targetif(dp[target] == target) return true;else return false;}
}
学习时间:
- 上午两个半小时,整理文档半小时。
相关文章:

代码随想录算法训练营第四十二天 _ 动态规划_01背包问题、416.分割等和子集。
学习目标: 动态规划五部曲: ① 确定dp[i]的含义 ② 求递推公式 ③ dp数组如何初始化 ④ 确定遍历顺序 ⑤ 打印递归数组 ---- 调试 引用自代码随想录! 60天训练营打卡计划! 学习内容: 二维数组处理01背包问题 听起来…...

市场上好用的aspera替代方案,你知道哪些
Aspera作为一个高速文件传输方案曾经非常受欢迎,但是其昂贵的价格却限制了许多用户的选择,因此市场上出现了众多Aspera替代方案,本文将会介绍市场上最好的Aspera替代方案。 最近几年,网络传输已成为现代商业运作中必不可少的一部…...

Stm32_串口的帧(不定长)数据接收
目录标题 前言1、串口中断接收固定帧头帧尾数据1.1、任务需求1.2、实现思路1.3、程序源码: 2、串口中断接收用定时器来判断帧结束3、串口中断接收数据空闲中断3.1、串口的空闲中断3.2、实现思路3.3、程序源码 4、串口的空闲中断DMA转运4.1、DMA简介4.2、DMA模式4.3、…...

L0、Linux常用命令
一、防火墙: 在 Linux 中,关闭防火墙可以使用不同的命令,这取决于你所使用的防火墙软件。在一些常见的 Linux 发行版中,防火墙可能是 iptables 或 firewalld两种: centos6使用iptables作为默认防火墙;cento…...

Golang实践录:读取toml配置
本文对 toml 文件进行解析。 下载 对于toml格式文件,golang 有很多库可以解释 yaml 文件,如toml、viper。由于 viper 可解析格式较多,本文采用该库。 toml语法规则 toml语法规则在官方中文文档上有说明,这里直接使用。 TOML 是…...
超大规模集成电路设计----基于阵列的可编程逻辑(七)
本文仅供学习,不作任何商业用途,严禁转载。本篇文章绝大部分资料来自中国科学院段成华教授PPT 超大规模集成电路设计----基于阵列的可编程逻辑(七) 7.1 引言7.1.1.回顾7.1.2. 数字逻辑系列Digital Logic Families7.1.3.从定制到半…...

深入探索FastAPI单元测试:使用TestClient轻松测试你的API
原文:深入探索FastAPI单元测试:使用TestClient轻松测试你的API-51CTO.COM 当使用FastAPI进行单元测试时,一个重要的工具是TestClient类。TestClient类允许我们模拟对FastAPI应用程序的HTTP请求,并测试应用程序的响应。这使我们能…...

基于ssm小型企业办公自动化系统论文
摘 要 互联网发展至今,无论是其理论还是技术都已经成熟,而且它广泛参与在社会中的方方面面。它让信息都可以通过网络传播,搭配信息管理工具可以很好地为人们提供服务。针对小型企业办公信息管理混乱,出错率高,信息安全…...

CasADi - 最优控制开源 Python/MATLAB 库
系列文章目录 文章目录 系列文章目录前言一、介绍1.1 CasADi 是什么?1.2 帮助与支持1.3 引用 CasADi1.4 阅读本文档 二、获取与安装三、符号框架3.1 符号 SX3.1.1 关于命名空间的说明3.1.2 C 用户注意事项 3.2 DM3.3 符号 MX3.4 SX 和 MX 混合使用3.5 稀疏类3.5.1 获…...

Java中使用String字符串的注意事项
引言 介绍字符串在Java中的重要性和普遍性,以及本文将讨论的注意事项。 1. 字符串是不可变的 解释Java中字符串是不可变的概念,即一旦创建,字符串对象的值就不能被修改。强调在对字符串进行操作时应当创建新的字符串对象而不是修改原有的对…...
离线数仓构建案例一
数据采集 日志数据(文件)到Kafka 自己写个程序模拟一些用户的行为数据,这些数据存在一个文件夹中。 接着使用flume监控采集这些文件,然后发送给kafka中待消费。 1、flume采集配置文件 监控文件将数据发给kafka的flume配置文件…...

nginx优雅如何优雅的接管【跨域配置】
跨域问题太常见了,这里不做详细赘述。文章主要想说一下,如何统一管理和更好的来管理 跨域配置 跨域的常见配置有两种 后台代码设置和网关设置 1、后台代码设置 以springboot为例代码如下(水一下文章长度...) Configuration pu…...

远离危险的购买手机的渠道
今年上半年从淘宝特价版上面的官方旗舰店买了一个oppo手机,第一次买我打算不要了,所以就退了回去,过了几天我又觉得还是买一个比较好,所以就又买了一个,型号我绝不说了700-1000z这个价位的手机带个高通骁龙芯片的&…...

外包干了2个多月,技术明显有退步了。。。。。
先说一下自己的情况,本科生,19年通过校招进入武汉某软件公司,干了接近4年的功能测试,今年国庆,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...

【Java项目管理工具】Maven
Maven 文章目录 Maven一、简介二、安装和配置三、GAVP四、IDEA Maven Java Web工程五、插件、命令、生命周期六、依赖配置七、构建配置八、依赖传递与依赖冲突九、Maven工程继承和聚合关系9.1 工程继承关系9.2 工程聚合关系 十、Maven私服10.1 Nexus下载安装10.2 Nexus上的各种…...
solidity案例详解(六)服务评价合约
有服务提供商和用户两类实体,其中服务提供商部署合约,默认诚信为true,用户负责使用智能合约接受服务及评价,服务提供商的评价信息存储在一个映射中,可以根据服务提 供商的地址来查找评价信息。用户评价信息,…...

使用kubeadm搭建高可用的K8s集群
文章目录 1. 安装要求2. 准备环境3. 所有master节点部署keepalived3.1 安装相关包和keepalived3.2配置master节点3.3 启动和检查 4. 部署haproxy4.1 安装4.2 配置4.3 启动和检查 5. 所有节点安装Docker/kubeadm/kubelet5.1 安装Docker5.2 添加阿里云YUM软件源5.3 安装kubeadm&a…...
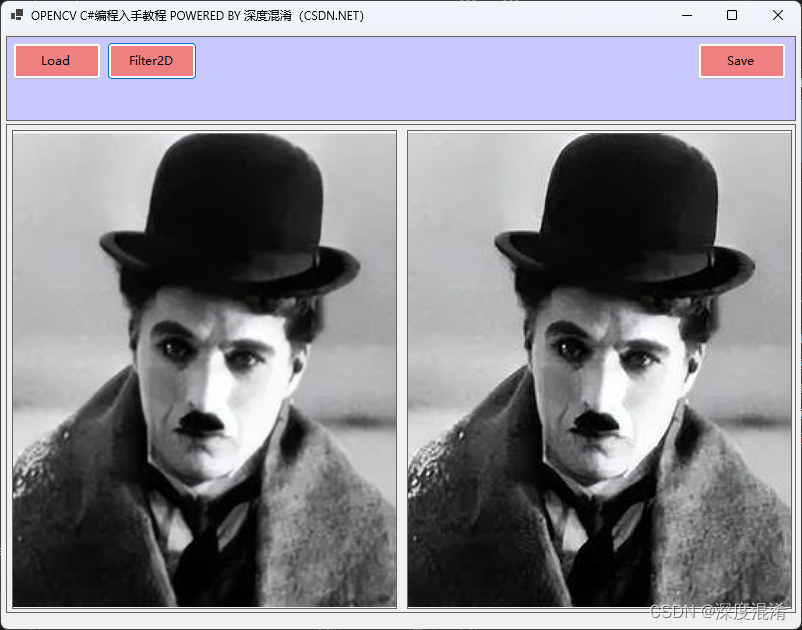
C#图像处理OpenCV开发指南(CVStar,07)——通用滤波(Filter2D)的实例代码
1 函数定义 void Filter2D (Mat src, Mat dst, int ddepth, InputArray kernel, Point anchor Point(-1,-1), double delta 0, int borderType BORDER_DEFAULT ) 1.1 原型 #include <opencv2/imgproc.hpp> Convolves an image wit…...

c++函数模板STL详解
函数模板 函数模板语法 所谓函数模板,实际上是建立一个通用函数,其函数类型和形参类型不具体指定,用一个虚拟的类型来代表。这个通用函数就称为函数模板。 凡是函数体相同的函数都可以用这个模板来代替,不必定义多个函数…...

Java利用UDP实现简单群聊
一、创建新项目 首先新建一个新的项目,并按如下操作 二、实现代码 界面ChatFrame类 package 群聊; import javax.swing.*; import java.awt.*; import java.awt.event.*; import java.net.InetAddress; public abstract class ChatFrame extends JFrame { p…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...
