Spatial Data Analysis(六):空间优化问题
Spatial Data Analysis(六):空间优化问题
使用pulp库解决空间优化问题:
pulp是一个用于优化问题的Python库。它包含了多种优化算法和工具,可以用于线性规划、混合整数线性规划、非线性规划等问题。Pulp提供了一个简单的方式来定义优化问题,包括变量、约束和目标函数,并且可以使用多种求解器进行求解。Pulp也提供了可视化工具来展示优化问题的结果。Pulp是一个开源项目,可以在GitHub上获取它的源代码。
空间优化(一):p-中值问题
这个问题需要p设施的位置,同时最小化服务所有需求的总加权距离。
每个节点都有一个关联的权重,表示该节点的需求量。
目标函数: 最小化所有设施和需求节点的需求加权总和。
决策变量: 将设施放置在何处以及哪个设施位置为哪些需求节点提供服务
限制:
- 每个节点由 1 个设施提供服务
- 仅当某个位置存在设施时,节点才可以由该设施提供服务。
- 我们必须放置p设施
- 每个节点要么是一个设施,要么不是。
pip install -q pulp
from pulp import *
import numpy as np
import geopandas as gp
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt
#read a sample shapefile
georgia_shp = gp.read_file("https://raw.githubusercontent.com/Ziqi-Li/GEO4162C/main/data/georgia/G_utm.shp")
georgia_shp.shape
(172, 18)
创建一个需求和一个设施变量,表示每个需求和设施的索引。
需求节点:所有县
facility:设施将建在一些选定的县之上
#create a demand and a facilities variable, indicating the indices of each demand and facility.
#demand node: all counties
#facility: Facilities will be built on top of some chosen countiesdemand = np.arange(0,172,1)
facilities = np.arange(0,172,1)
计算距离矩阵d_ij(n×n)
#Calculate a distance matrix d_ij (n by n)
coords = list(zip(georgia_shp.centroid.x,georgia_shp.centroid.y))d = cdist(coords,coords)
每个县(hi)的需求是总人口
#the demand for each county (h_i) is the total populatoion
h = georgia_shp.TotPop90.values
声明设施变量;生成的变量名称为:X_1,X_2,…
# declare facilities variables;the resulting variable names are: X_1,X_2,...
X = LpVariable.dicts('X_%s',(facilities),cat='Binary')# declare demand-facility pair variables; the resulting variable names are Y_0_1, Y_0_2,...
Y = LpVariable.dicts('Y_%s_%s', (demand,facilities),cat='Binary')
要放置的设施数量
#Number of facilities to place
p = 3 #change this and re-run the code.#Create a new problem
prob = LpProblem('P_Median', LpMinimize)
目标函数:最小化所有设施和需求节点的加权需求距离总和
(h_i: i 处的需求;d_ij: i 和 j 之间的距离)
“for”循环用于迭代序列
# Objective function: Minimizing weighted demand-distance summed over all facilities and demand nodes
# (h_i: demand at i; d_ij: distance between i and j)
# A "for" loop is used for iterating over a sequenceprob += sum(sum(h[i] * d[i][j] * Y[i][j] for j in facilities) for i in demand)
这个约束表明我们必须精确放置 p 个设施
# This constraint indicates we must place exactly p facilitiesprob += sum([X[j] for j in facilities]) == p
这一约束意味着需求节点 i 只能由一个设施提供服务
# This constraint implies that a demand node i can only be serviced by one facilityfor i in demand:prob += sum(Y[i][j] for j in facilities) == 1
这个约束意味着需求节点 i
仅当 j 处有设施时才能由 j 处的设施提供服务
它隐式地消除了 X[j] = 0 但 Y[i][j] = 1 时的情况
(节点 i 由 j 提供服务,但 j 处没有设施)
# This constraint implies that that demand node i
# can be serviced by a facility at j only if there is a facility at j
# It implicitly removes situation when X[j] = 0 but Y[i][j] = 1
# (node i is served by j but there is no facility at j)for i in demand:for j in facilities:prob += Y[i][j] <= X[j]
%%time# Solve the above problem
prob.solve()print("Status:", LpStatus[prob.status])
Status: Optimal
CPU times: user 1.35 s, sys: 64 ms, total: 1.42 s
Wall time: 11.5 s
# The minimized total demand-distance. The unit is person * meter (total distance travelled)
print("Objective: ",value(prob.objective))
Objective: 469538765110.4489
# Print the facility node.
rslt=[]
for v in prob.variables():subV = v.name.split('_')if subV[0] == "X" and v.varValue == 1:rslt.append(int(subV[1]))print('Facility Node: ', subV[1])
Facility Node: 126
Facility Node: 30
Facility Node: 82
# Get the geomerty of the facility nodes.
fac_loc = georgia_shp.iloc[rslt,:]
fac_loc
| AREA | PERIMETER | G_UTM_ | G_UTM_ID | AREANAME | Latitude | Longitud | TotPop90 | PctRural | PctBach | PctEld | PctFB | PctPov | PctBlack | X | Y | AreaKey | geometry | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 126 | 7.315030e+08 | 117190.0 | 130 | 128 | GA, Crisp County | 31.92540 | -83.77159 | 20011 | 48.4 | 10.0 | 12.47 | 0.30 | 29.0 | 40.66 | 805648.4 | 3537103 | 13081 | POLYGON ((787012.250 3547615.750, 820243.312 3... |
| 30 | 1.385270e+09 | 274218.0 | 32 | 31 | GA, Fulton County | 33.78940 | -84.46716 | 648951 | 4.2 | 31.6 | 9.63 | 4.13 | 18.4 | 49.92 | 733728.4 | 3733248 | 13121 | POLYGON ((752606.688 3785970.500, 752835.062 3... |
| 82 | 9.179670e+08 | 121744.0 | 84 | 84 | GA, Jenkins County | 32.78866 | -81.96042 | 8247 | 53.8 | 7.7 | 13.10 | 0.21 | 27.8 | 41.51 | 970465.7 | 3640263 | 13165 | POLYGON ((989566.750 3653155.750, 981378.062 3... |
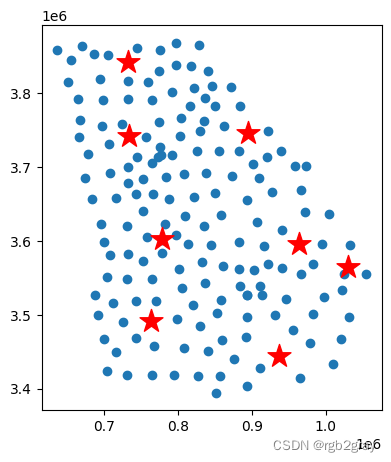
#Plot the faclities (stars) on top of the demand map.
fig, ax = plt.subplots(figsize=(5,5))georgia_shp.centroid.plot(ax=ax,markersize=georgia_shp.TotPop90/1000)#markersize is proportional to the population
fac_loc.centroid.plot(ax=ax,color="red",markersize=300,marker="*")

空间优化(二):集合覆盖问题
在此模型中,设施可以为距设施给定覆盖距离 Dc 内的所有需求节点提供服务。 问题在于放置最少数量的设施,以确保所有需求节点都能得到服务。 我们假设设施没有容量限制。
pip install -q pulp
from pulp import *
import numpy as np
import geopandas as gp
from scipy.spatial.distance import cdistimport matplotlib.pyplot as plt
#read a sample shapefile
georgia_shp = gp.read_file("https://raw.githubusercontent.com/Ziqi-Li/GEO4162C/main/data/georgia/G_utm.shp")
georgia_shp.shape
(172, 18)
创建一个需求和一个设施变量,表示每个需求和设施的索引。
需求节点:所有县
facility:我们可以在一些县建造设施
#create a demand and a facilities variable, indicating the indices of each demand and facility.
#demand node: all counties
#facility: we could build facilities in some countiesdemand = np.arange(0,172,1)
facilities = np.arange(0,172,1)
计算距离矩阵d_ij(n×n)
#Calculate a distance matrix d_ij (n by n)
coords = list(zip(georgia_shp.centroid.x,georgia_shp.centroid.y))
d = cdist(coords,coords)
阈值覆盖距离
# Threshold coverage distance
Dc = 100000 #100km coverage, change this and re run the code.
创建一个变量,指示节点 i 是否可以被设施 j 覆盖。
#Creata a variable (alpha in the lecture slide pg.28), indicating whether a node i can be covered by facility j.
a = np.zeros(d.shape)
a[d <= Dc] = 1
a[d > Dc] = 0
声明设施变量 Xj
# declare facilities variables Xj
X = LpVariable.dicts('X_%s',(facilities),cat='Binary')
创建一个最小化问题
#Create an minimization problem
prob = LpProblem('Set_Covering', LpMinimize)
目标函数:我们要最小化放置设施的数量
# Objective function: we want to minimize the number of placed facilities
prob += sum([X[j] for j in facilities])
该约束意味着每个需求节点 i 需要至少由设施服务
# This constraint implies every demand node i needs to be served by at least facility
for i in demand:prob += sum(a[i][j]*X[j] for j in facilities) >= 1%%time
# Solve the above problem
prob.solve()print("Status:", LpStatus[prob.status])
Status: Optimal
CPU times: user 22.5 ms, sys: 1.05 ms, total: 23.6 ms
Wall time: 66.4 ms
# The minimal number of facilities with the defiened coverage.
print("Objective: ",value(prob.objective))
Objective: 8.0
# Print the facility nodes.
rslt = []
for v in prob.variables():subV = v.name.split('_')if subV[0] == "X" and v.varValue == 1:rslt.append(int(subV[1]))print('Facility Node: ', subV[1])
Facility Node: 102
Facility Node: 120
Facility Node: 145
Facility Node: 150
Facility Node: 30
Facility Node: 38
Facility Node: 9
Facility Node: 97
# Get the geomerty of the facility nodes.
fac_loc = georgia_shp.iloc[rslt,:]
#Plot the faclities (stars) on top of the demand map.
fig, ax = plt.subplots(figsize=(5,5))georgia_shp.centroid.plot(ax=ax)
fac_loc.centroid.plot(ax=ax,color="red",markersize=300,marker="*")
<Axes: >
相关文章:

Spatial Data Analysis(六):空间优化问题
Spatial Data Analysis(六):空间优化问题 使用pulp库解决空间优化问题: pulp是一个用于优化问题的Python库。它包含了多种优化算法和工具,可以用于线性规划、混合整数线性规划、非线性规划等问题。Pulp提供了一个简单…...

PHP短信接口防刷防轰炸多重解决方案三(可正式使用)
短信接口盗刷轰炸:指的是黑客利用非法手段获取短信接口的访问权限,然后使用该接口发送大量垃圾短信给目标用户 短信验证码轰炸解决方案一(验证码类解决)-CSDN博客 短信验证码轰炸解决方案二(防止海外ip、限制ip、限制手机号次数解决)-CSDN博客 PHP短信…...
C#大型LIS检验信息系统项目源码
LIS系统,一套医院检验科信息系统。它是以数据库为核心,将实验仪器与电脑连接成网,基础功能包括病人样本登录、实验数据存取、报告审核、打印分发等。除基础功能外,实验数据统计分析、质量控制管理、人员权限管理、试剂出入库等功能…...
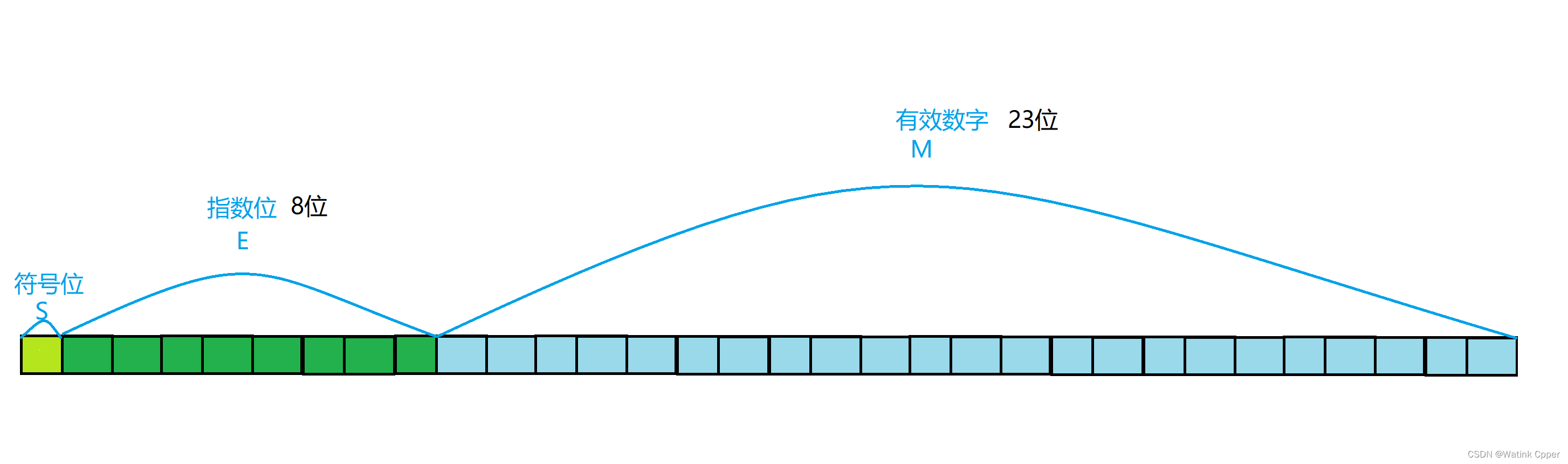
【C语言】数据在内存中的存储
目录 练笔 整型数据的存储: char 型数据——最简单的整型 整型提升: 推广到其他整形: 大小端: 浮点型数据的存储: 存储格式: 本篇详细介绍 整型数据,浮点型数据 在计算机中是如何储存的。…...
Java聊天程序(一对一)简单版
我们首先要完成服务端,不然出错,运行也要先运行服务端,如果不先连接服务端,就不监听,那客户端不知道连接谁 服务端 import java.awt.BorderLayout; import java.awt.event.ActionEvent; import java.awt.event.Actio…...

Linux下超轻量级Rust开发环境搭建:一、安装Rust
Rust语言在国内逐步开始流行,但开发环境的不成熟依然困扰不少小伙伴。 结合我个人的使用体验,推荐一种超轻量级的开发环境:Rust Helix Editor。运行环境需求很低,可以直接在Linux终端里进行代码开发。对于工程不是太过庞大的Rus…...

定义一个学生类,其中有3个私有数据成员学号、姓名、成绩,以及若于成员。 函数实现对学生数据的赋值和输出。
#include <stdio.h> // 定义学生类 typedef struct Student { int stuNum; // 学号 char name[20]; // 姓名,假设最长为20个字符 float score; // 成绩 } Student; // 初始化学生信息 void initializeStudent(Student *student, int num, const…...
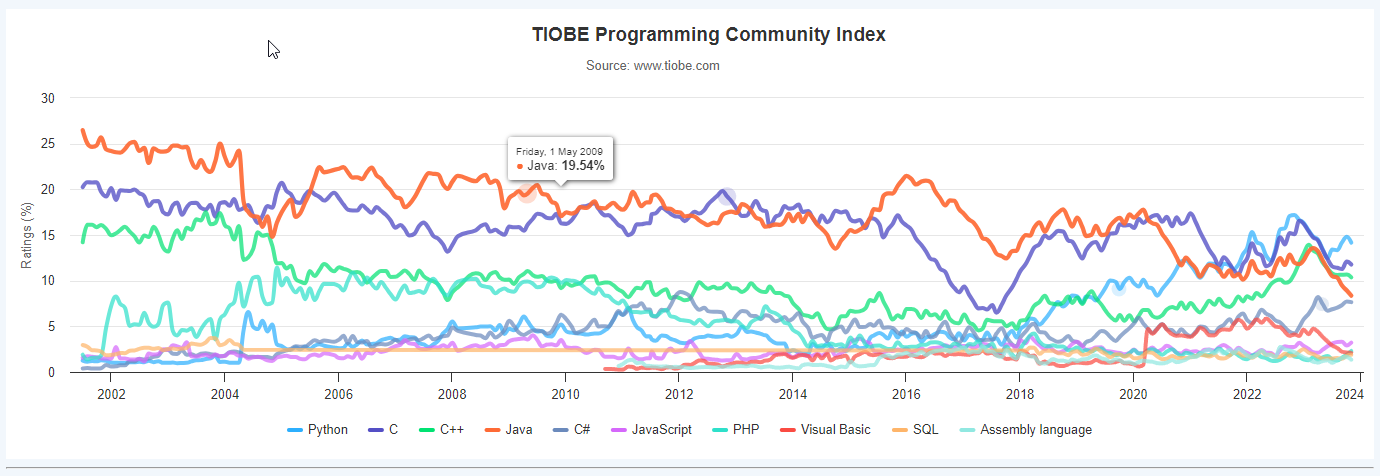
1.2 C语言简介
一、为什么要讲C语言 C语言是编程界的长青藤,可以查看语言排名发现,虽然现在语言很多,但是C语言一直占有一定地址 来源网站:https://www.tiobe.com/tiobe-index/ 在系统、嵌入式、底层驱动等领域存在一定的唯一性(C语…...

小白学Java之数组问题——第三关黄金挑战
内容1.数组中出现次数超过一般的数字2.数组中出现一次的数字3.颜色分类问题 1.数组中出现次数超过一半的数字 这是剑指offer中的一道题目,数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。 例如:输入如下所示的一个长度为9…...
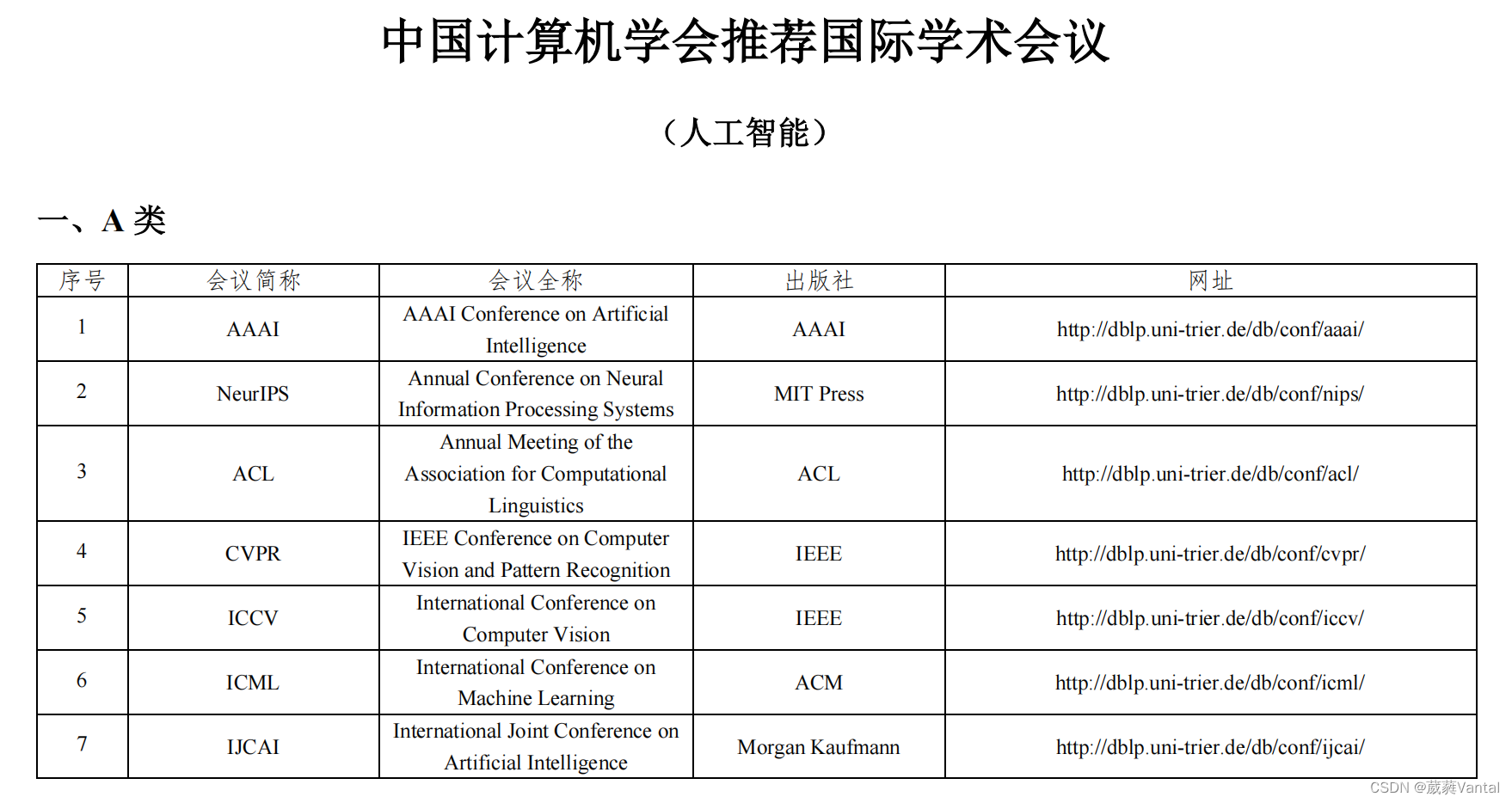
各大期刊网址
1.NeurIPS,全称Annual Conference on Neural Information Processing Systems, 是机器学习领域的顶级会议,与ICML,ICLR并称为机器学习领域难度最大,水平最高,影响力最强的会议! NeurIPS是CCF 推…...

使用autodl服务器,在A40显卡上运行, Yi-34B-Chat-int4模型,并使用vllm优化加速,显存占用42G,速度18 words/s
1,演示视频 https://www.bilibili.com/video/BV1gu4y1c7KL/ 使用autodl服务器,在A40显卡上运行, Yi-34B-Chat-int4模型,并使用vllm优化加速,显存占用42G,速度18 words/s 2,关于A40显卡…...
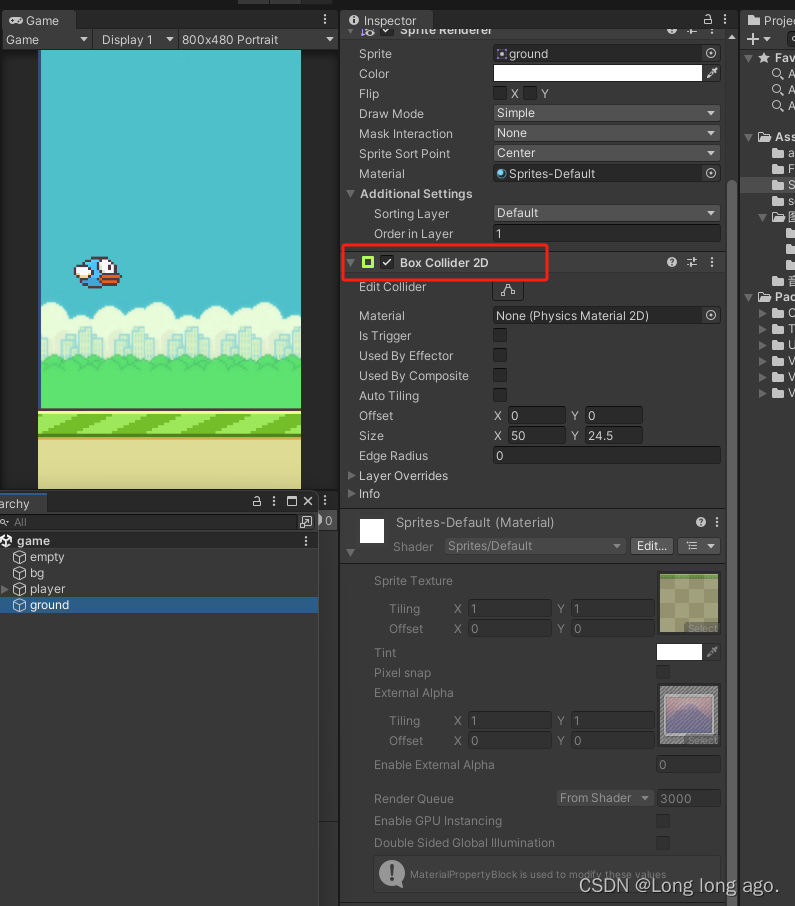
unity 2d 入门 飞翔小鸟 下坠功能且碰到地面要停止 刚体 胶囊碰撞器 (四)
1、实现对象要受重力 在对应的图层添加刚体 改成持续 2、设置胶囊碰撞器并设置水平方向 3、地面添加盒状碰撞器 运行则能看到小鸟下坠并落到地面上...
速达软件任意文件上传漏洞复现
简介 速达软件专注中小企业管理软件,产品涵盖进销存软件,财务软件,ERP软件,CRM系统,项目管理软件,OA系统,仓库管理软件等,是中小企业管理市场的佼佼者,提供产品、技术、服务等信息,百万企业共同选择。速达软件全系产品存在任意文件上传漏洞,未经身份认证得攻击者可以通过此漏…...

Name or service not knownstname
Name or service not knownstname Hadoop 或 Spark 集群启动时 报错 Name or service not knownstname 原因时因为 workers 文件在windows 使用图形化工具打开过 操作系统类型不对引发的 在Linux系统上删除 workers 文件 使用 vim 重新编辑后分发即可...
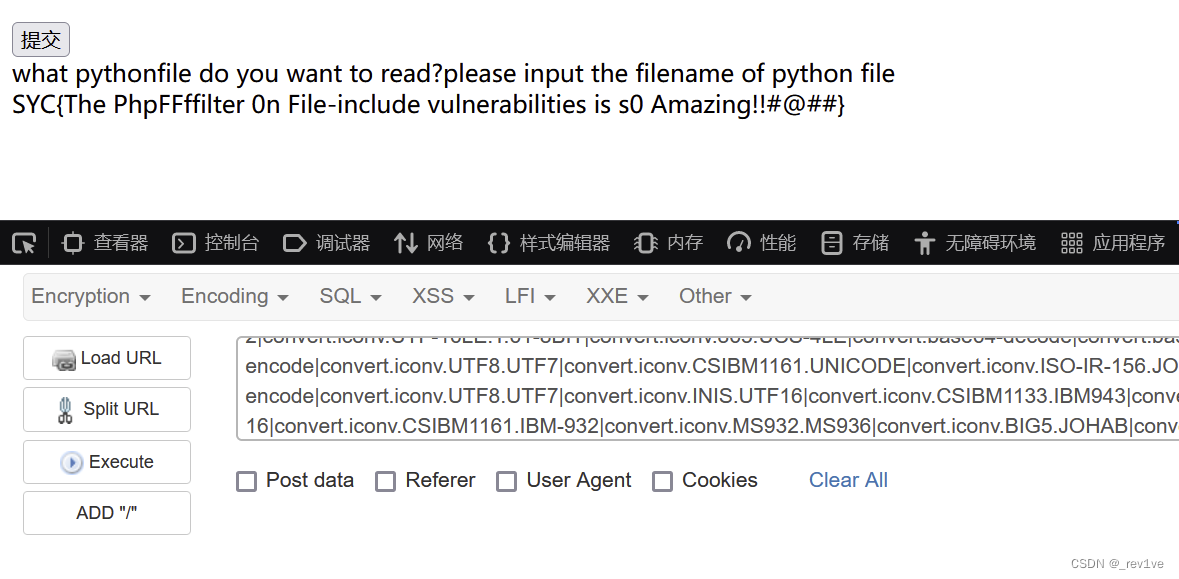
[Geek Challenge 2023] web题解
文章目录 EzHttpunsignn00b_Uploadeasy_phpEzRceezpythonezrfi EzHttp 按照提示POST传参 发现密码错误 F12找到hint,提示./robots.txt 访问一下,得到密码 然后就是http请求的基础知识 抓包修改 最后就是 我们直接添加请求头O2TAKUXX: GiveMeFlag 得到…...

【recrutment / Hiring / Job / Application】
Interviewee I), objected/targeted job/position1.1) Azure 平台运维工程师(comms&social)1.1.1), comms communication and social, for talk, content1.1.2) Cloud computing1.1.3) 拥有ITI/MCSE/RHCE相关认证或Azure认证(如Az204/Az304 have/own…...
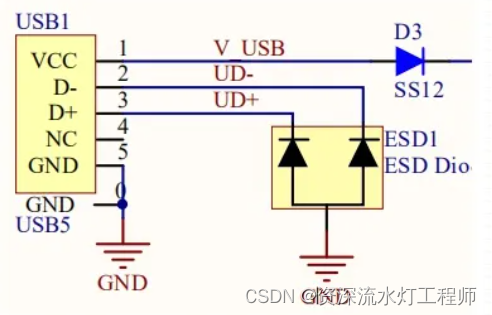
二极管:ESD静电保护二极管
一、什么是ESD二极管 ESD二极管与 TVS二极管原理是一样的,也是为了保护电,但ESD二极管的主要功能是防止静电。 静电防护的前提条件就要求其电容值要足够地低,一般在1PF-3.5PF之间最好,主要应用于板级保护。 二、什么是静电 静…...

【根据数组元素生成随机颜色函数】
const colorOptions ["#f50","#2db7f5","#87d068","#108ee9",];const getRandomColor () > {const randomIndex Math.floor(Math.random() * colorOptions.length);return colorOptions[randomIndex];}; 时小记,终有…...
鸿蒙一出,android开发处境再受重创
华为宣布其自研操作系统鸿蒙HarmonyOSNEXT开发者预览版将不再兼容安卓系统,这一消息引起了广泛关注和热议。这一决策标志着华为正式告别安卓,摆脱了外部的制约,开始着手打造一个全新的生态系统。 鸿蒙系统4发布一个月,截至目前&a…...

ruoyi+Hadoop+hbase实现大数据存储查询
前言 有个现实的需求,数据量可能在100亿条左右。现有的数据库是SQL Server,随着采集的数据不断的填充,查询的效率越来越慢(现有的SQL Server查询已经需要数十秒钟的时间),看看有没有优化的方案。 考虑过S…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...
