当前位置： 首页 > news >正文

计算两个结构的差

news 2025/12/4 6:57:06

平面上有6个点，以6a1的方式运动

1

1

1

1

-

-

-

1

-

-

-

1

现在有一个点逃逸，剩下的5个点将如何运动？

2

2

2

3

-

-

-

3

-

-

-

3

将6a1的6个点减去1个点，只有两种可能，或者变成5a2，或者变成5a3，二者比例是1：1

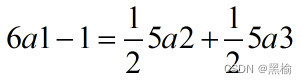
所以这平面上的6个点，在一个点飞出的瞬间，剩下的5个点运动方式只能有两种可能。

算第二种可能，如果同时飞出2个点

4a7

2a3

1

1

1

-

1

-

1

1

-

1

-

-

=

-

1

-

+

-

-

-

-

1

-

1

-

-

-

-

-

-

-

1

-

-

1

-

-

-

4a1

2a1

1

1

1

-

1

1

1

-

-

1

-

-

=

-

1

-

+

1

-

-

-

1

-

-

-

1

-

-

-

-

-

1

-

-

-

-

-

-

4a2

2a2

1

1

1

-

1

1

1

-

-

1

-

-

=

-

-

1

+

-

1

-

-

1

-

1

-

-

-

-

-

-

-

1

-

-

-

-

-

-

4a4

2a2

1

1

1

-

-

1

1

-

-

1

-

-

=

1

1

1

+

-

1

-

-

1

-

-

-

-

-

-

-

-

-

1

-

-

-

-

-

-

将6a1按照4+2的方式分解，有4种可能，占比为，

4a7

2a3

3

4a1

2a1

3

4a2

2a2

6

4a4

2a2

3

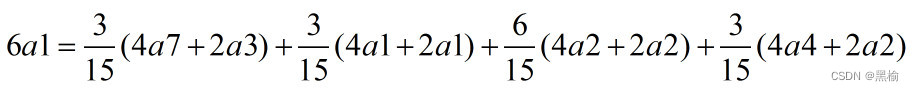
所以如果已知两个点按照2a2的方式飞出，

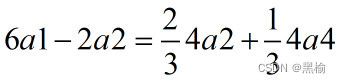
剩余的4个点，有2/3的可能按照4a2的方式运动，有1/3的可能按照4a4的方式运动。

假如一次飞出3个点

3a5

3a6

1

1

1

1

-

-

1

1

1

1

-

-

=

-

1

-

+

-

-

-

-

1

-

-

-

1

-

-

-

-

-

1

-

-

-

-

-

-

3a3

3a1

1

1

1

-

-

1

1

1

-

1

-

-

=

-

-

1

+

-

1

-

-

1

-

1

-

-

-

-

-

-

-

1

-

-

-

-

-

-

3a5

3a4

1

1

1

1

-

-

1

1

-

1

-

-

=

-

1

-

+

-

-

1

-

1

-

-

-

1

-

-

-

-

-

1

-

-

-

-

-

-

6a1按照3+3的方式分解有3种可能，占比为

3a5

3a6

1

3a3

3a1

6

3a5

3a4

3

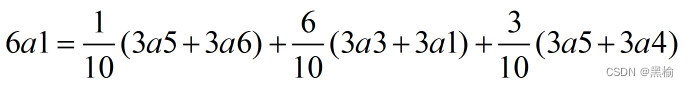
所以如果已知3个点按照3a5的方式飞出，

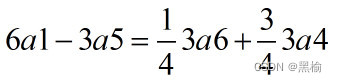
剩余的3个点有1/4的可能按照3a6的方式运动，有3/4的可能按照3a4的方式运动。是一个复合态。

所以如果有一个函数φ1把直线上的n个点，映射为平面上的一种运动方式比如结构x，而另一个函数φ2把平面上的m个点映射为平面上的另一种运动方式结构y，现在φ1和φ2之间作用的结果就取决于两个结构x，y，只要x和y是已知的φ1和φ2的作用结果就是可计算的，而不必知道φ1和φ2的解析式。

相关文章：

计算两个结构的差

平面上有6个点，以6a1的方式运动 1 1 1 1 - - - 1 - - - 1 现在有一个点逃逸，剩下的5个点将如何运动？ 2 2 2 3 - - - 3 - - - 3 将6a1的6个点减去1个点，只有两种可能，或者变成5a2&#xff0c…...

编程日记 2023/12/7 22:41:00

class037 二叉树高频题目-下-不含树型dp【算法】

class037 二叉树高频题目-下-不含树型dp【算法】 code1 236. 二叉树的最近公共祖先 // 普通二叉树上寻找两个节点的最近公共祖先 // 测试链接 : https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/ package class037;// 普通二叉树上寻找两个节点的最近…...

编程日记 2023/12/7 22:37:57

使用cpolar完成内网穿刺

cpolar官网上有一句评论：cpolar是用过最简单的内网穿刺工具！ 实际体验下来，cpolar确实是能够非常简单地实现内网穿刺 先说弊端，免费版的cpolar提供的穿刺地址，有效期为一天，进程连接数有限，如…...

编程日记 2023/12/7 22:35:55

git的使用:基础配置和命令行

前言 代码管理工具,任何开发都离不开的话题。 到了任何公司,第一件事肯定是配置个人的电脑。主要就是三点,配置对应的开发环境,配置各类开发工具和配置git等代码管理工具拉取代码。 这篇文章主要是git的配置和最常用(我指的是最常用)的命令行使用 git基础配置 git的安装 …...

编程日记 2023/12/7 22:30:51

若依微服务项目整合rocketMq

原文链接：ttps://mp.weixin.qq.com/s/IYdo_suKvvReqCiEKjCeHw 第一步下载若依项目 第二步安装rocketMq（推荐在linux使用docker部署比较快） 第二步新建一个生产者模块儿，再建一个消费者模块 第四步在getway模块中配置接口映射规…...

编程日记 2023/12/7 22:29:50

连接服务器的ssh终端自动断开解放方法

在Linux中，SSH连接在一段时间内没有活动时可能会自动断开，这是为了安全性考虑的一种默认行为，以防止未经授权的访问。这个时间限制通常由SSH服务器的配置决定。你可以通过以下几种方式来处理这个问题： 1.使用SSH配置文件&#xf…...

编程日记 2023/12/7 22:22:45

Windows+WSL开发环境下微服务注册（Consul)指定IP

Win11下安装一个WSL2，做开发环境，简直是爽到不要不要的，相当于既有Windows下的完善生态，又有linux的便利。特别是，在linux下运行的服务端口号，完全和windows是相通的，直接在windows下浏览访问&a…...

编程日记 2023/12/7 22:20:43

通过K8S安装人大金仓数据库

1. 离线下载镜像&#xff0c;请点击 2. 官网下载镜像 https://www.kingbase.com.cn/xzzx/index.htm&#xff0c;根据自己的需求下载对应版本。 3. K8S需要的yaml清单 cat > kingbase.yaml << EOF apiVersion: apps/v1 kind: Deployment metadata:name: kingbase-…...

编程日记 2023/12/7 22:19:41

正则表达式（3）：入门

正则表达式&#xff08;3&#xff09;&#xff1a;入门 小结 本博文转载自 从这篇文章开始&#xff0c;我们将介绍怎样在Linux中使用”正则表达式”&#xff0c;如果你想要学习怎样在Linux中使用正则表达式&#xff0c;这些文章就是你所需要的。 在认识”正则表达式”之前&am…...

编程日记 2023/12/7 22:18:40

《系统架构设计师教程（第2版）》第2章-计算机系统基础知识-01-计算机硬件

文章目录 1. 计算机系统概述2. 计算机硬件2.1 处理器（CPU）2.2 存储器2.2.1 概述2.2.2 按硬件结构分类2.2.3 按与处理器距离分2.3 总线(Bus)2.3.1 概念2.3.2 分类2.3.3 串行总线和并行总线2.4 接口2.4.1 概念2.4.2 常见接口2.5 外部设备1. 计算机系统概述 #mermaid-svg-IcU0sR…...

编程日记 2023/12/7 22:17:38

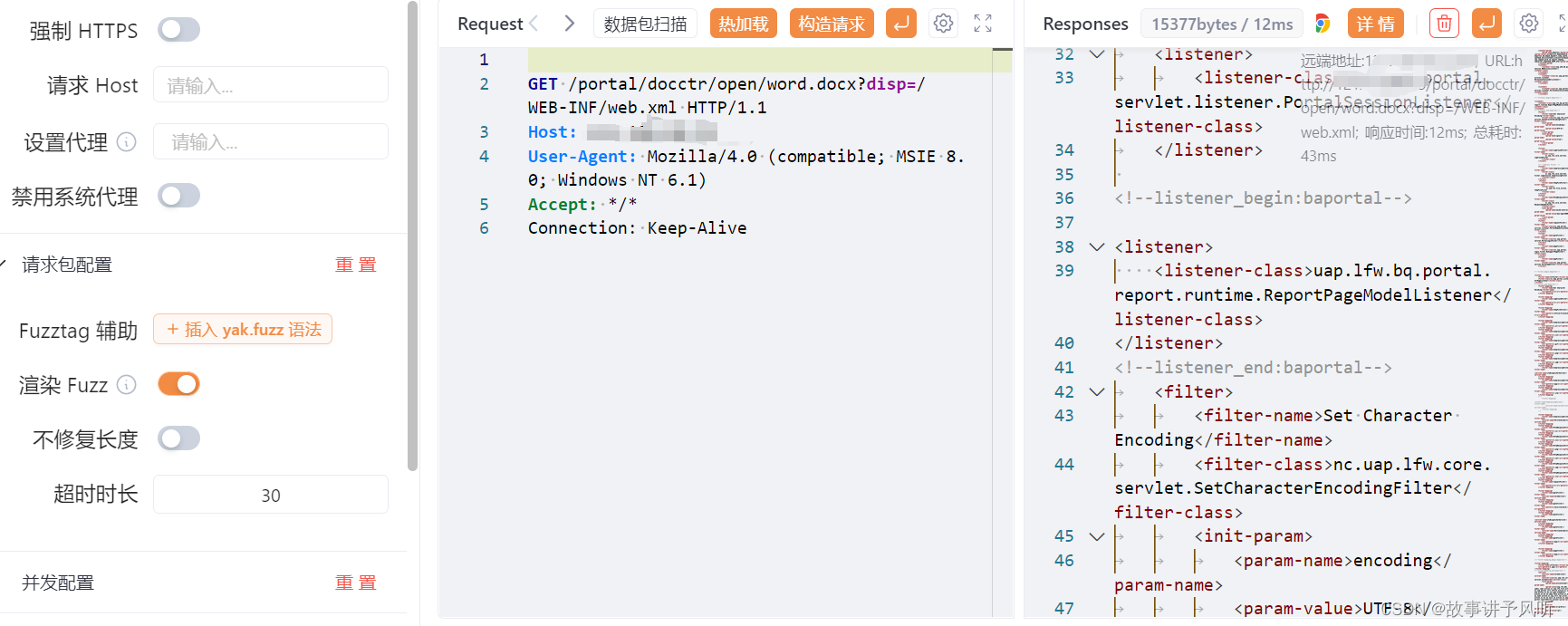
用友NC word.docx接口存在任意文件读取漏洞

声明 本文仅用于技术交流&#xff0c;请勿用于非法用途 由于传播、利用此文所提供的信息而造成的任何直接或者间接的后果及损失&#xff0c;均由使用者本人负责&#xff0c;文章作者不为此承担任何责任。 一、产品介绍 用友 NC Cloud&#xff0c;大型企业数字化平台&#xff…...

编程日记 2023/12/7 22:15:37

【离散数学】——期末刷题题库（等价关系与划分）

&#x1f383;个人专栏&#xff1a; &#x1f42c; 算法设计与分析&#xff1a;算法设计与分析_IT闫的博客-CSDN博客 &#x1f433;Java基础&#xff1a;Java基础_IT闫的博客-CSDN博客 &#x1f40b;c语言&#xff1a;c语言_IT闫的博客-CSDN博客 &#x1f41f;MySQL&#xff1a…...

编程日记 2023/12/7 22:12:34

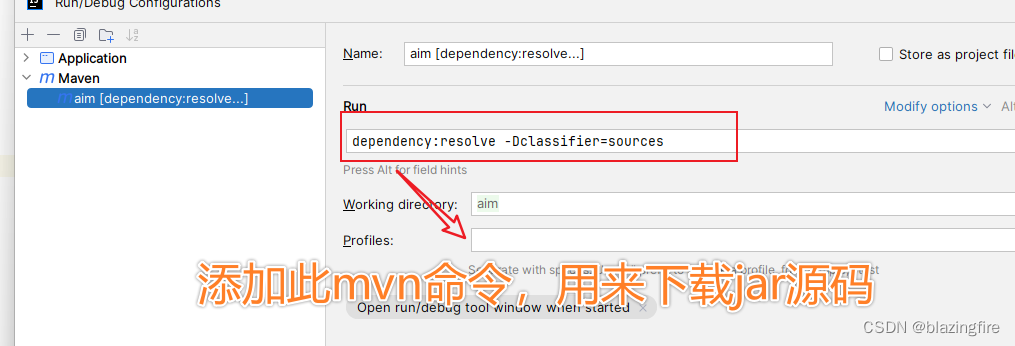
IDEA maven无法下载源代码处理

1、使用idea内置maven 在idea中新增一个mvn运行项,截图如下: 输入命令: dependency:resolve -Dclassifiersources 2、如果外部maven&#xff0c;不使用idea内部maven 在工程目录下命令行执行命令: mvn dependency:resolve -Dclassifiersources...

编程日记 2023/12/7 22:11:33

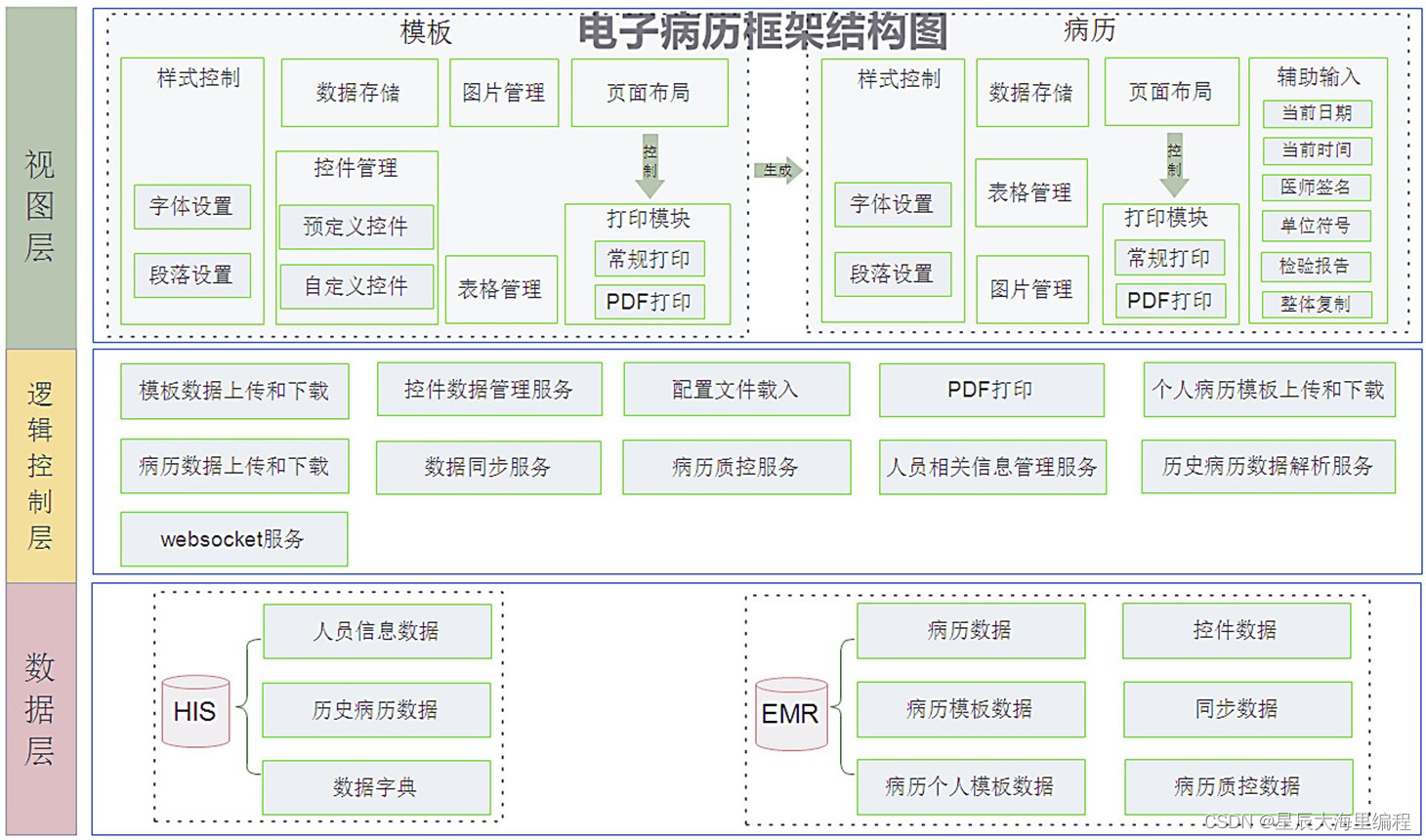
基于B/S架构的医院一体化电子病历编辑器源码

电子病历在线制作、管理和使用的一体化电子病历解决方案&#xff0c;通过一体化的设计&#xff0c;提供对住院病人的电子病历书写、保存、修改、打印等功能。电子病历系统将临床医护需要的诊疗资料以符合临床思维的方法展示。建立以病人为中心&#xff0c;以临床诊疗信息为主线…...

编程日记 2023/12/7 22:08:30

免费百度SEO优化工具,百度SEO优化排名工具

百度SEO关键词工具 让我们聚焦在百度SEO关键词工具上。对于任何想要在百度搜索引擎中脱颖而出的网站管理员而言&#xff0c;深入了解用户搜索习惯和关键词的选择是至关重要的。 百度SEO关键词工具不仅提供了免费的服务&#xff0c;而且功能强大。通过输入相关领域的关键词&…...

编程日记 2023/12/7 22:06:29

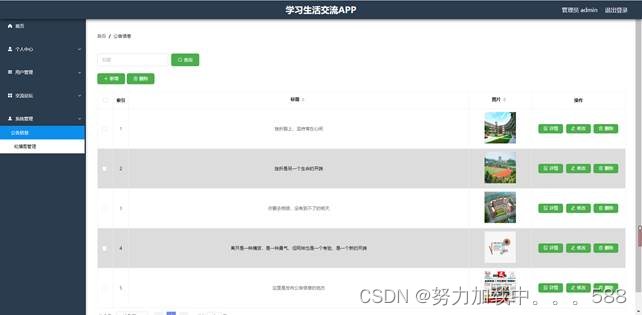
12.Java程序设计-基于Springboot框架的Android学习生活交流APP设计与实现

摘要 移动应用在日常生活中扮演着越来越重要的角色&#xff0c;为用户提供了方便的学习和生活交流渠道。本研究旨在设计并实现一款基于Spring Boot框架的Android学习生活交流App&#xff0c;以促进用户之间的信息分享、学术交流和社交互动。 在需求分析阶段&#xff0c;我们明…...

编程日记 2023/12/7 22:05:28

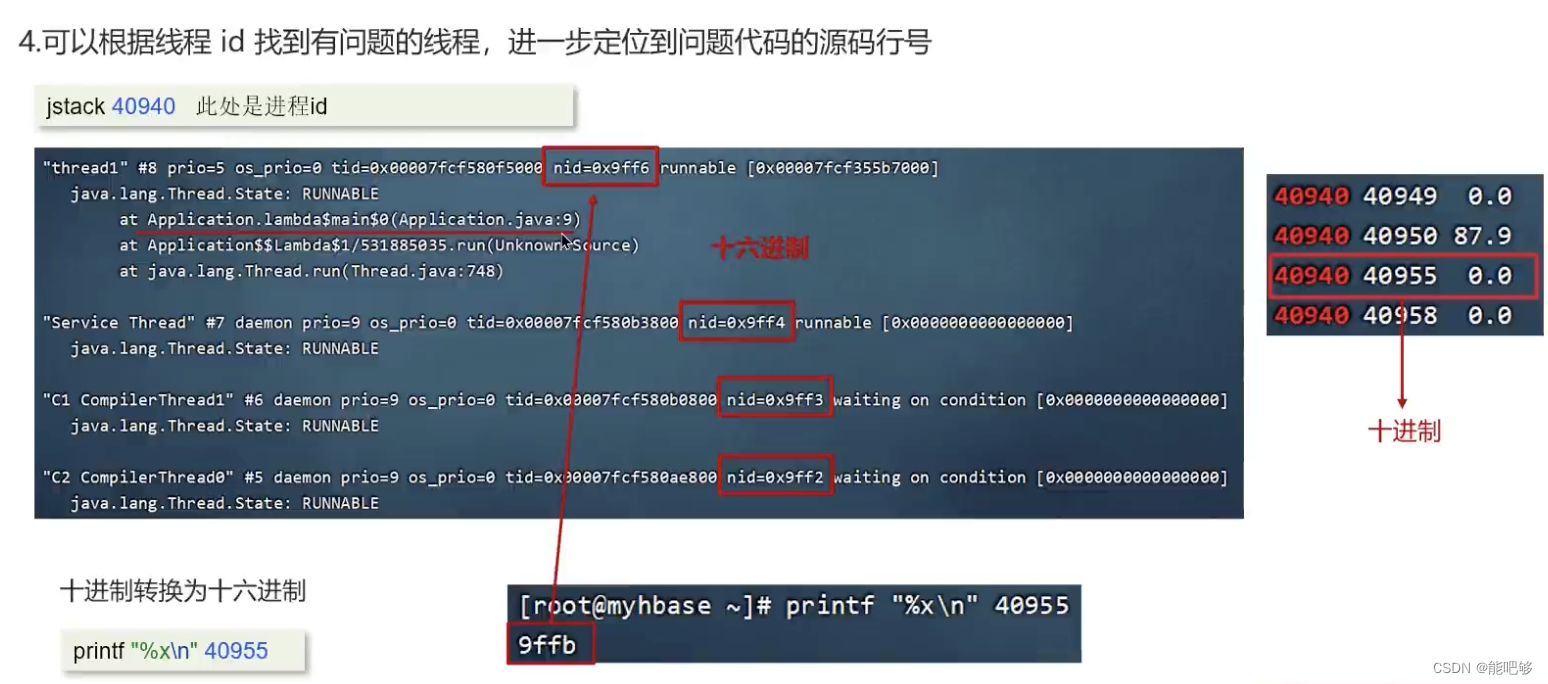
JVM虚拟机（已整理，已废弃）

# JVM组成 ## 简述程序计数器 线程私有&#xff0c;内部保存class字节码的行号。用于记录正在执行的字节码指令的地址。 线程私有-每个线程都有自己的程序计数器PC&#xff0c;用于记录当前线程执行哪个行号 ## 简述堆 ## 简述虚拟机栈 ## 简述堆栈区别 ## 方法内局部变量是…...

编程日记 2023/12/7 22:04:27

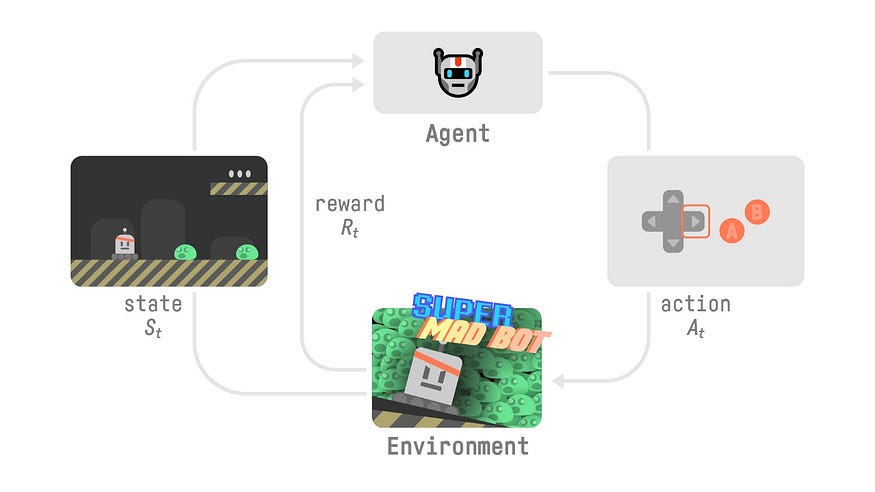
强化学习——简单解释

一、说明 最近 OpenAI 上关于 Q-star 的热议激起了我温习强化学习知识的兴趣。这是为强化学习 (RL) 新手提供的复习内容。 二、强化学习的定义 强化学习是人类和其他动物用来学习的学习类型。即&#xff0c;通过阅读房间来学习。&#xff08;从反馈中学习&#xff09;。让我解…...

编程日记 2023/12/7 22:01:25

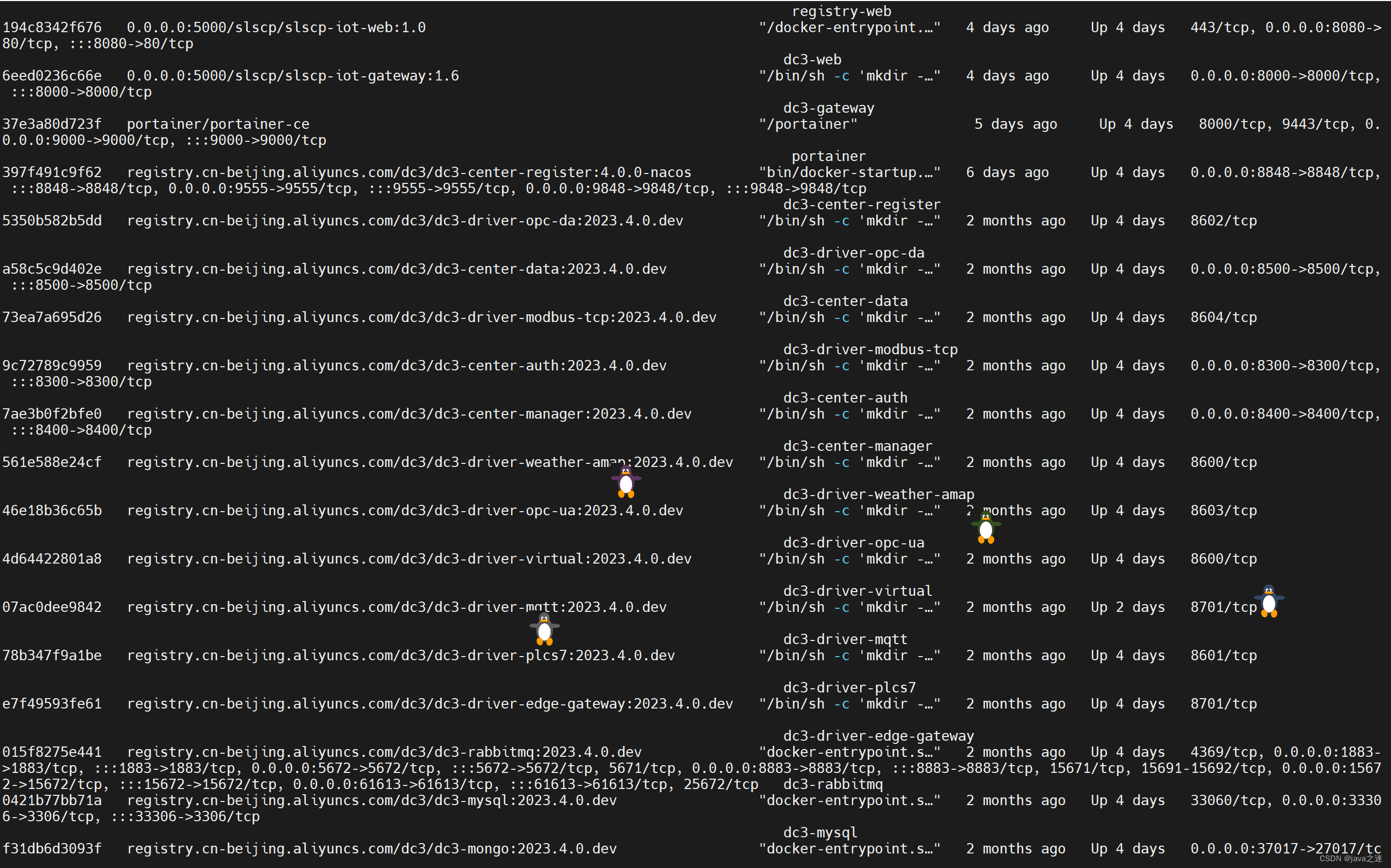
IoT DC3 是一个基于 Spring Cloud 全开源物联网平台 linux docker部署傻瓜化步骤

如有不了解可先参考我的另一篇文章本地部署:IoT DC3 是一个基于 Spring Cloud 的开源的、分布式的物联网(IoT)平台本地部署步骤 如有不了解可先参考我的另一篇文章本地部署: 1 环境准备: JDK 8 以上 docker 安装好 下载docker-compose-dev.yml 文件 执行基础环境docker安装 …...

编程日记 2023/12/7 22:00:24

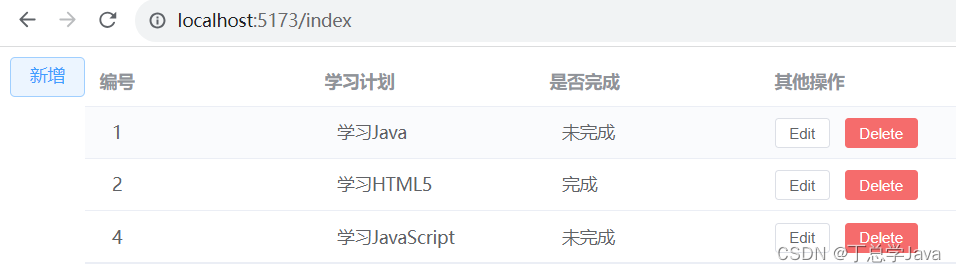
SSM项目实战-前端-在Index.vue中展示第一页数据

1、util/request.js import axios from "axios";let request axios.create({baseURL: "http://localhost:8080",timeout: 50000 });export default request 2、api/schedule.js import request from "../util/request.js";export let getSchedu…...

编程日记 2023/12/7 21:59:23

Python爬虫实战：研究MechanicalSoup库相关技术

一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库，专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力，提供了直观的 API，让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

编程新知 2025/10/10 18:13:55

Docker 离线安装指南

参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性&#xff0c;不同版本的Docker对内核版本有不同要求。例如&#xff0c;Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本&#xff0c;Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

编程新知 2025/12/3 17:54:20

C++初阶-list的底层

目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

编程新知 2025/11/25 12:53:08

css实现圆环展示百分比，根据值动态展示所占比例

代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

编程新知 2025/12/2 9:58:47

Admin.Net中的消息通信SignalR解释

定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

编程新知 2025/9/10 5:36:56

8k长序列建模，蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂

蛋白质结合剂&#xff08;如抗体、抑制肽&#xff09;在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上&#xff0c;高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术&#xff0c;但这类方法普遍面临资源消耗巨大、研发周期冗长…...

编程新知 2025/12/3 9:53:08

Docker 运行 Kafka 带 SASL 认证教程

Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明&#xff1a;server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

编程新知 2025/12/3 2:24:58

使用分级同态加密防御梯度泄漏

抽象 联邦学习 &#xff08;FL&#xff09; 支持跨分布式客户端进行协作模型训练&#xff0c;而无需共享原始数据&#xff0c;这使其成为在互联和自动驾驶汽车 &#xff08;CAV&#xff09; 等领域保护隐私的机器学习的一种很有前途的方法。然而&#xff0c;最近的研究表明&…...

编程新知 2025/12/4 3:58:47

vue3 字体颜色设置的多种方式

在Vue 3中设置字体颜色可以通过多种方式实现&#xff0c;这取决于你是想在组件内部直接设置&#xff0c;还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法&#xff1a; 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

编程新知 2025/10/6 20:49:11

cf2117E

原题链接&#xff1a;https://codeforces.com/contest/2117/problem/E 题目背景&#xff1a; 给定两个数组a,b&#xff0c;可以执行多次以下操作&#xff1a;选择 i (1 < i < n - 1)&#xff0c;并设置 或&#xff0c;也可以在执行上述操作前执行一次删除任意 和 。求…...

编程新知 2025/12/1 22:22:07