Oracle中mybatis批量更新报错ORA-00933:SQL命令未正确结束
项目场景:
最近在开发项目的过程中遇见了这个问题:Oracle中批量更新的时候报错 ORA-00933:SQL命令未正确结束
问题描述
mybatis批量更新报错ORA-00933:SQL命令未正确结束
<foreach item="item" index="index" collection="list" separator=";">update Aset ID=#{item.id}where NAME=#{item.name}
</foreach>
上边这个执行的时候报错ORA-00933:SQL命令未正确结束
原因分析:
oracle中数据库批量更新和mysql中的有些不一样,需要进行如下修改。
解决方案:
对上边的代码进行改变
- separator=“;” 这个里边一定要加分号,而不是逗号
- begin和end必须要成对出现 open=“begin” end=“;end;” 也就是为了补全语法
<foreach item="item" index="index" collection="list" open="begin" end=";end;" separator=";">update Aset ID=#{item.id}where NAME=#{item.name}
</foreach>
相关文章:

Oracle中mybatis批量更新报错ORA-00933:SQL命令未正确结束
项目场景: 最近在开发项目的过程中遇见了这个问题:Oracle中批量更新的时候报错 ORA-00933:SQL命令未正确结束 问题描述 mybatis批量更新报错ORA-00933:SQL命令未正确结束 <foreach item"item" index"index&q…...

Mysql综合案例练习<1>
MySql综合案例练习<1> 题目一题目二题目三题目四题目五题目六题目七题目八题目九题目十题目十一题目十二题目十三题目十四题目十五题目十六题目十七题目十八题目十九 题目一 创建数据库test01_library 创建表 books,表结构如下: CREATE DATABASE …...
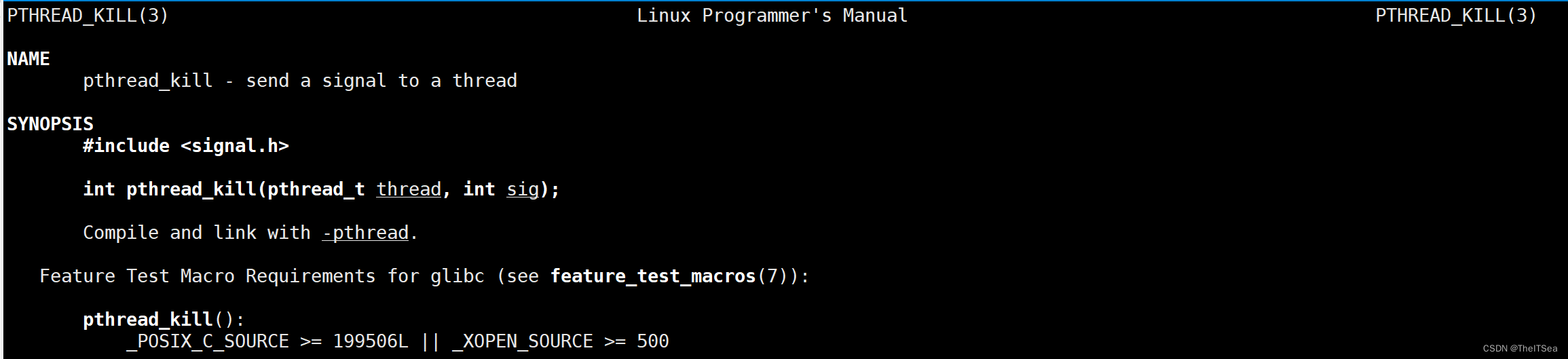
Linux系统编程:线程总结
线程的概念 基本概念 所谓线程,通俗的说就是一个正在运行的函数。 在Linux系统中,线程是程序运行的最小单位,也被视为进程内部的控制序列。同一进程下的多个线程共享进程的所有资源,包括进程环境变量、打开的文件描述符、信号量…...

activemq启动成功但web管理页面却无法访问
前提: 在linux启动activemq成功!本地能ping通linux 处理方案: 确定防火墙是否关闭, 有两种处理方案:第一种-关闭防火墙;第二种-暴漏8161和61616两个端口 netstat -lnpt查看8161和61616端口 注意…...

【Flink on k8s】- 0 - Flink kubernetes operator 快速入门与实战
完整的课程,请点击链接。 目录 一、你将收获 二、适用人群 三、课程介绍...

毕设:《基于hive的音乐数据分析系统的设计与实现》
文章目录 环境启动一、爬取数据1.1、歌单信息1.2、每首歌前20条评论1.3、排行榜 二、搭建环境1.1、搭建JAVA1.2、配置hadoop1.3、配置Hadoop环境:YARN1.4、MYSQL1.5、HIVE(数据仓库)1.6、Sqoop(关系数据库数据迁移) 三、hadoop配置内存四、导…...

PHP使用HTTP代码示例模板
PHP是一种广泛用于服务器端的编程语言,它提供了许多内置的函数和扩展,以便开发人员能够轻松地处理HTTP请求和响应。在PHP中,您可以使用以下代码示例模板来处理HTTP请求和生成HTTP响应。 php复制代码 <?php // 处理GET请求 if ($…...
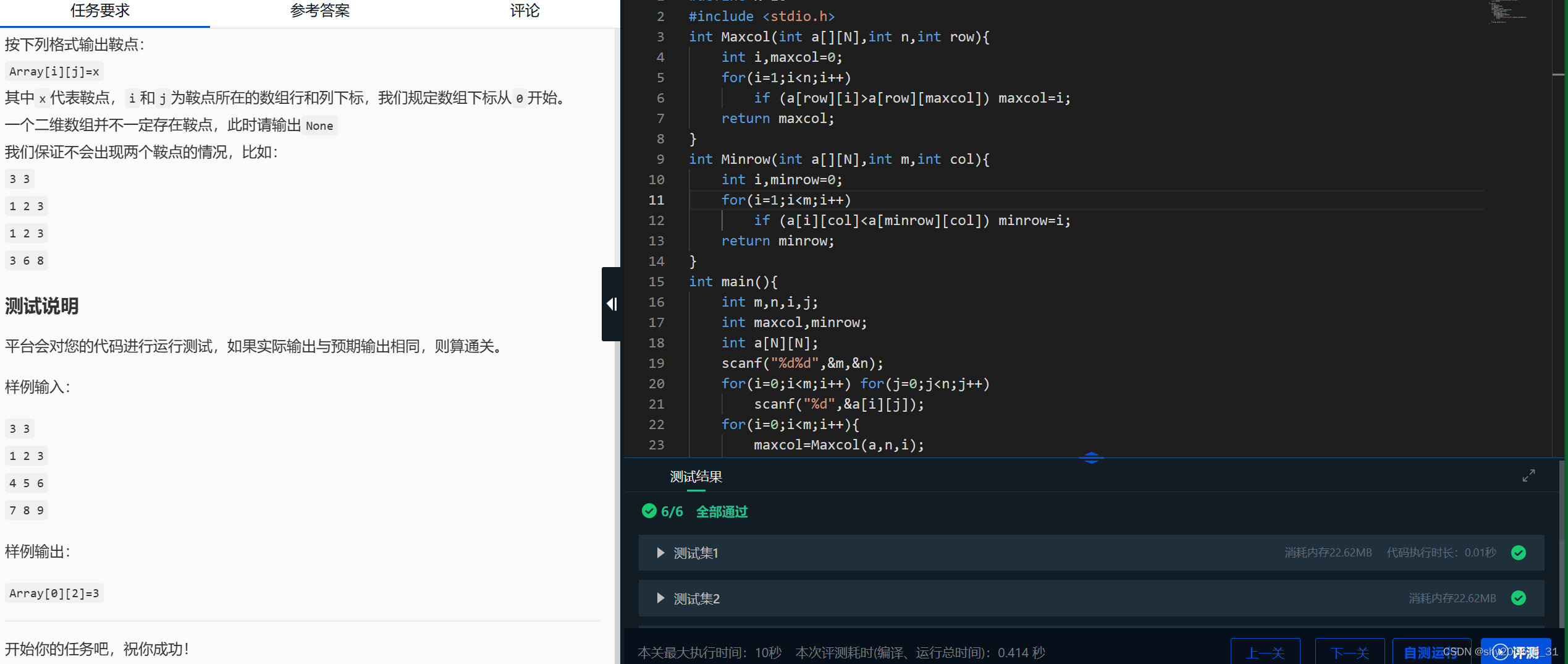
头歌题目-数组
任务描述 题目描述:找出具有m行n列二维数组Array的“鞍点”,即该位置上的元素在该行上最大,在该列上最小,其中1<m,n<10。 相关知识(略) 编程要求 输入 输入数据有多行,第一行有两个数m和n&#…...

C++ vector基本操作
目录 一、介绍 二、定义 三、迭代器 四、容量操作 1、size 2、capacity 3、empty 4、resize 5、reserve 总结(扩容机制) 五、增删查改 1、push_back & pop_back 2、find 3、insert 4、erase 5、swap 6、operator[] 一、介绍 vector…...
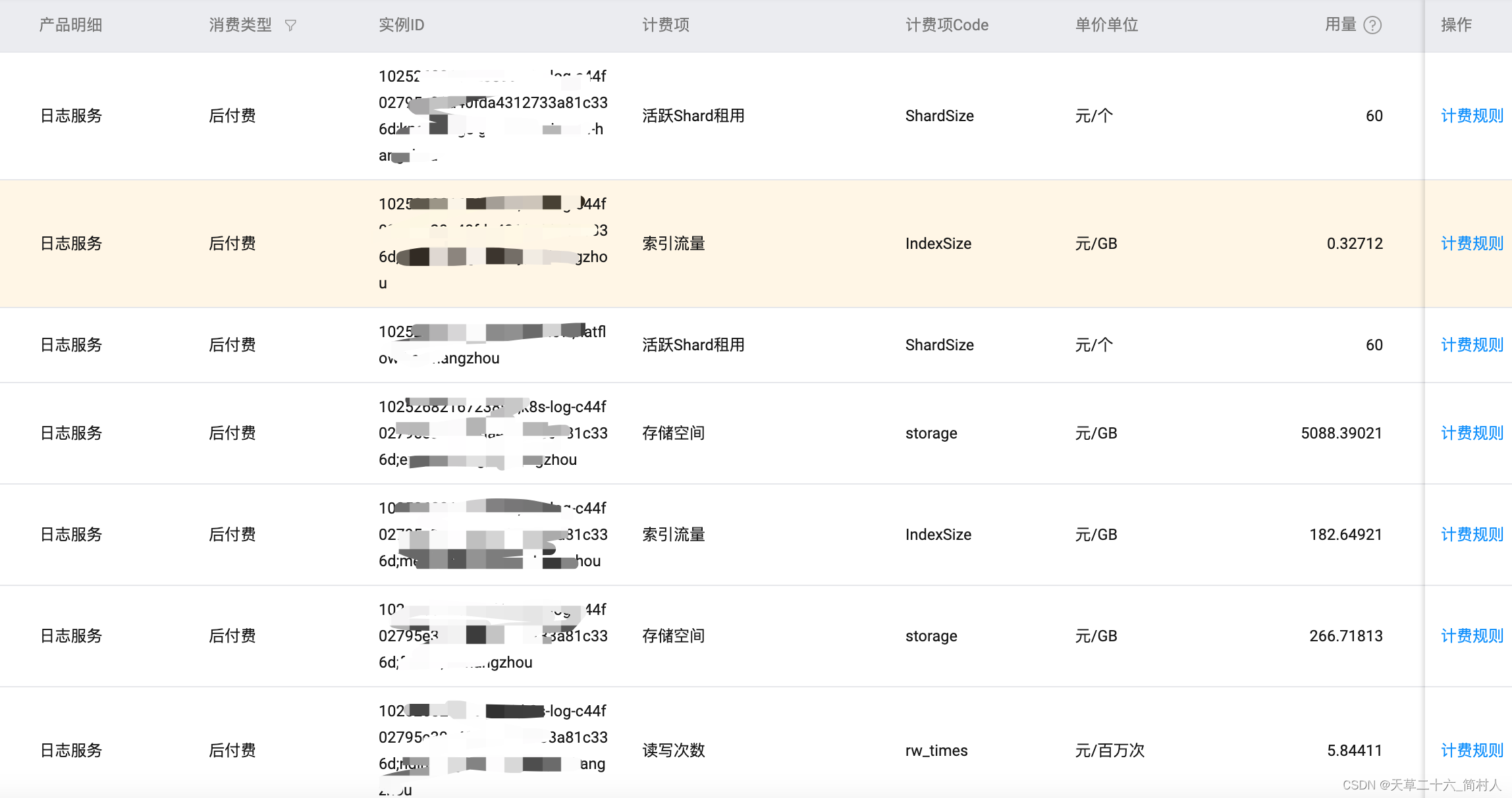
使用SLS日志服务采集Kong网关的日志
一、阿里云SLS 官方的接入文档已比较丰富了,本文不意重复说明此事。 站在使用的角度,以采集Kong的日志为示例,说明我们应该如何治理日志。 说白了,本文是想给你怎么省钱作一个建议,希望不会让你公司也“降本增笑”。…...
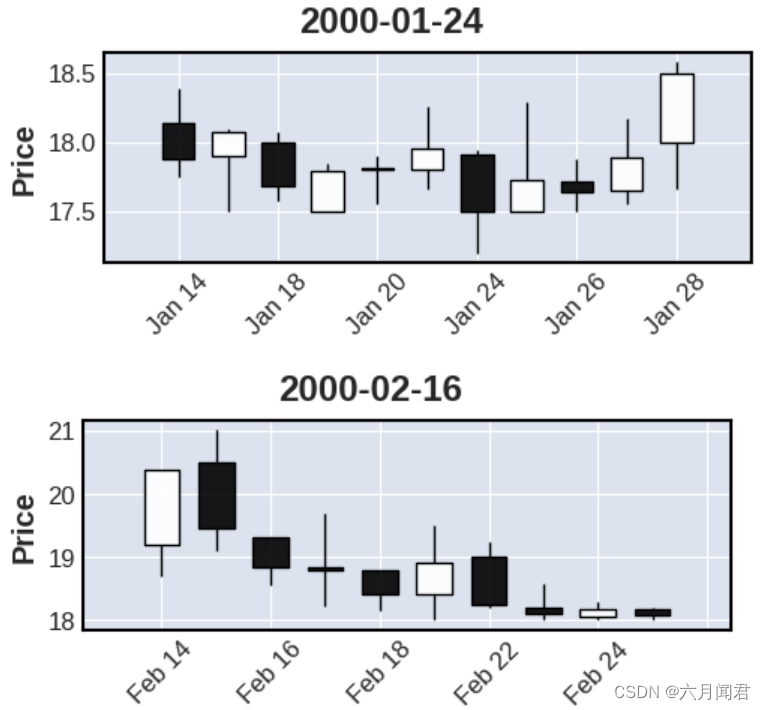
TA-Lib学习研究笔记(九)——Pattern Recognition (1)
TA-Lib学习研究笔记(九)——Pattern Recognition (1) 0.程序代码 形态识别的函数的应用,通过使用A股实际的数据,验证形态识别函数,用K线显示出现标志的形态走势,由于入口参数基本上…...
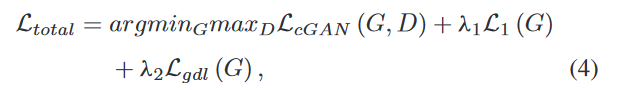
基于GAN的多尺度门合并多模态MRI图像合成
Multi-Modal MRI Image Synthesis via GAN With Multi-Scale Gate Mergence 基于GAN的多尺度门合并多模态MRI图像合成背景贡献实验方法生成器gate mergence (GM) strategy(门控融合策略)判别器 损失函数Thinking 基于GAN的多尺度门合并多模态MRI图像合成…...
浅谈https
1.网络传输的安全性 http 协议:不安全,未加密https 协议:安全,对请求报文和响应报文做加密 2.对称加密与非对称加密 2.1 对称加密 特点: 加解密使用 相同 秘钥 高效,适用于大量数据的加密场景 算法公开&a…...
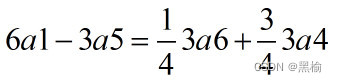
计算两个结构的差
平面上有6个点,以6a1的方式运动 1 1 1 1 - - - 1 - - - 1 现在有一个点逃逸,剩下的5个点将如何运动? 2 2 2 3 - - - 3 - - - 3 将6a1的6个点减去1个点,只有两种可能,或者变成5a2,…...

class037 二叉树高频题目-下-不含树型dp【算法】
class037 二叉树高频题目-下-不含树型dp【算法】 code1 236. 二叉树的最近公共祖先 // 普通二叉树上寻找两个节点的最近公共祖先 // 测试链接 : https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/ package class037;// 普通二叉树上寻找两个节点的最近…...
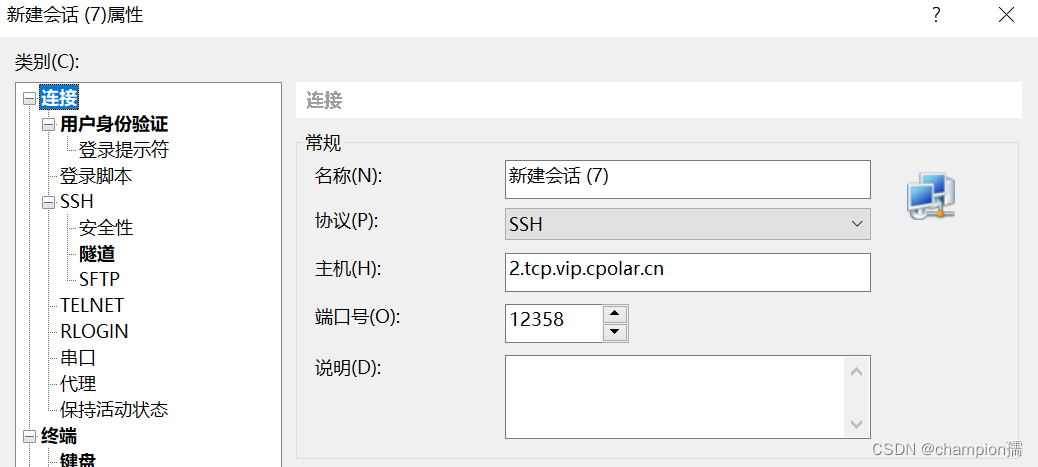
使用cpolar完成内网穿刺
cpolar官网上有一句评论:cpolar是用过最简单的内网穿刺工具! 实际体验下来,cpolar确实是能够非常简单地实现内网穿刺 先说弊端,免费版的cpolar提供的穿刺地址,有效期为一天,进程连接数有限,如…...

git的使用:基础配置和命令行
前言 代码管理工具,任何开发都离不开的话题。 到了任何公司,第一件事肯定是配置个人的电脑。主要就是三点,配置对应的开发环境,配置各类开发工具和配置git等代码管理工具拉取代码。 这篇文章主要是git的配置和最常用(我指的是最常用)的命令行使用 git基础配置 git的安装 …...
若依微服务项目整合rocketMq
原文链接:ttps://mp.weixin.qq.com/s/IYdo_suKvvReqCiEKjCeHw 第一步下载若依项目 第二步安装rocketMq(推荐在linux使用docker部署比较快) 第二步新建一个生产者模块儿,再建一个消费者模块 第四步在getway模块中配置接口映射规…...

连接服务器的ssh终端自动断开解放方法
在Linux中,SSH连接在一段时间内没有活动时可能会自动断开,这是为了安全性考虑的一种默认行为,以防止未经授权的访问。这个时间限制通常由SSH服务器的配置决定。你可以通过以下几种方式来处理这个问题: 1.使用SSH配置文件…...
指定IP)
Windows+WSL开发环境下微服务注册(Consul)指定IP
Win11下安装一个WSL2,做开发环境,简直是爽到不要不要的,相当于既有Windows下的完善生态,又有linux的便利。特别是,在linux下运行的服务端口号,完全和windows是相通的,直接在windows下浏览访问&a…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...
