【深度学习】一维数组的聚类
在学习聚类算法的过程中,学习到的聚类算法大部分都是针对n维的,针对一维数据的聚类方式较少,今天就来学习下如何给一维的数据进行聚类。
方案一:采用K-Means对一维数据聚类
Python代码如下:
- from sklearn.cluster import KMeans
- import numpy as np
- x = np.random.random(10000)
- y = x.reshape(-1,1)
- km = KMeans()
- km.fit(y)
核心的操作是y = x.reshape(-1,1),含义为将一维数据变成只有1列,行数不知道多少(-1代表根据剩下的维度计算出数组的另外一个shape属性值)。
方案二:采用一维聚类方法Jenks Natural Breaks
Jenks Natural Breaks(自然断点分类)。一般来说,分类的原则就是差不多的放在一起,分成若干类。统计上可以用方差来衡量,通过计算每类的方差,再计算这些方差之和,用方差和的大小来比较分类的好坏。因而需要计算各种分类的方差和,其值最小的就是最优的分类结果(但并不唯一)。这也是自然断点分类法的原理。另外,当你去看数据的分布时,可以比较明显的发现断裂之处,这些断裂之处和Jenks Natural Breaks方法算出来也是一致的。因而这种分类法很“自然”。
Jenks Natural Breaks和K Means在一维数据时,完全等价。它们的目标函数一样,但是算法的步骤不完全相同。K Means是先设定好K个初始随机点。而Jenks Breaks则是用遍历的方法,一个点一个点地移动,直到达到最小值。
Natural Breaks算法又有两种:
- Jenks-Caspall algorithm(1971),是Jenks和Caspall发明的算法。原理就如前所述,实现的时候要将每种分类情况都计算一遍,找到方差和最小的那一种,计算量极大。n个数分成k类,就要从n-1个数中找k-1个组合,这个数目是很惊人的。数据量较大时,如果分类又多,以当时的计算机水平根本不能穷举各种可能性。
- Fisher-Jenks algorithm(1977),Fisher(1958)发明了一种算法提高计算效率,不需要进行穷举。Jenks将这种方法引入到数据分类中。但后来者几乎只知道Jenks而不知Fisher了。
具体算法实现:
- Jenks-Caspall algorithm:https://github.com/domlysz/Jenks-Caspall.py
- Fisher-Jenks algorithm:https://github.com/mthh/jenkspy
和K-Means一样,使用Jenks Natural Breaks需要先确定聚类数量K值。常见的方法是:GVF(The Goodness of Variance Fit)。GVF,翻译过来是“方差拟合优度”,公式如下:
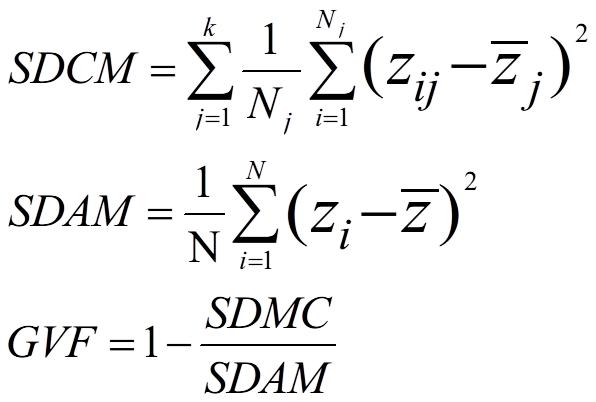
其中,SDAM是the Sum of squared Deviations from the Array Mean,即原始数据的方差;SDCM是the Sum of squared Deviations about Class Mean,即每一类方差的和。显然,SDAM是一个常数,而SDCM与分类数k有关。一定范围内,GVF越大,分类效果越好。SDCM越小,GVF越大,越接近于1。而SDCM随k的增大而大,当k等于n时,SDMC=0,GVF=1。
GVF用于判定不同分类数的分类效果好坏。以k和GVF做图可得:

随着k的增大,GVF曲线变得越来越平缓。特别是在红线处(k=5),曲线变得基本平坦(之前起伏较大,之后起伏较小),k(5)也不是很大,所以可以分为5类。一般来说,GVF>0.7就可以接受了,当然越高越好,但一定要考虑k不能太大。显然,这是一个经验公式,但总比没有好吧。
代码示例:
- from jenkspy import jenks_breaks
- import numpy as np
- def goodness_of_variance_fit(array, classes):
- # get the break points
- classes = jenks_breaks(array, classes)
- # do the actual classification
- classified = np.array([classify(i, classes) for i in array])
- # max value of zones
- maxz = max(classified)
- # nested list of zone indices
- zone_indices = [[idx for idx, val in enumerate(classified) if zone + 1 val] for zone in range(maxz)]
- # sum of squared deviations from array mean
- sdam = np.sum((array - array.mean()) 2)
- # sorted polygon stats
- array_sort = [np.array([array[index] for index in zone]) for zone in zone_indices]
- # sum of squared deviations of class means
- sdcm = sum([np.sum((classified - classified.mean()) 2) for classified in array_sort])
- # goodness of variance fit
- gvf = (sdam - sdcm) / sdam
- return gvf
- def classify(value, breaks):
- for i in range(1, len(breaks)):
- if value < breaks[i]:
- return i
- return len(breaks) - 1
- if name ‘main’:
- gvf = 0.0
- nclasses = 2
- array = np.random.random(10000)
- while gvf < .8:
- gvf = goodness_of_variance_fit(array, nclasses)
- print(nclasses, gvf)
- nclasses += 1
参考链接:
- https://en.wikipedia.org/wiki/Jenks_natural_breaks_optimization
- https://macwright.org/2013/02/18/literate-jenks.html
方案三:核密度估计Kernel Density Estimation
所谓核密度估计,就是采用平滑的峰值函数(“核”)来拟合观察到的数据点,从而对真实的概率分布曲线进行模拟。核密度估计更多详细内容,可以参考先前的Mean Shift聚类中的相关说明。
使用示例:
- import numpy as np
- from scipy.signal import argrelextrema
- import matplotlib.pyplot as plt
- from sklearn.neighbors.kde import KernelDensity
- a = np.array([10, 11, 9, 23, 21, 11, 45, 20, 11, 12]).reshape(-1, 1)
- kde = KernelDensity(kernel=‘gaussian’, bandwidth=3).fit(a)
- s = np.linspace(0, 50)
- e = kde.score_samples(s.reshape(-1, 1))
- plt.plot(s, e)
- plt.show()
- mi, ma = argrelextrema(e, np.less)[0], argrelextrema(e, np.greater)[0]
- print(“Minima:”, s[mi])
- print(“Maxima:”, s[ma])
- print(a[a < mi[0]], a[(a >= mi[0]) * (a <= mi[1])], a[a >= mi[1]])
- plt.plot(s[:mi[0] + 1], e[:mi[0] + 1], ‘r’,
- s[mi[0]:mi[1] + 1], e[mi[0]:mi[1] + 1], ‘g’,
- s[mi[1]:], e[mi[1]:], ‘b’,
- s[ma], e[ma], ‘go’,
- s[mi], e[mi], ‘ro’)
- plt.show()
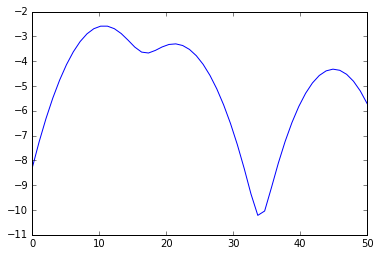
输出内容:
- Minima: [17.34693878 33.67346939]
- Maxima: [10.20408163 21.42857143 44.89795918]
- [10 11 9 11 11 12] [23 21 20] [45]

参考链接:
- https://en.wikipedia.org/wiki/Kernel_density_estimation
- http://scikit-learn.org/stable/auto_examples/neighbors/plot_kde_1d.html
- https://jakevdp.github.io/blog/2013/12/01/kernel-density-estimation/
相关文章:

【深度学习】一维数组的聚类
在学习聚类算法的过程中,学习到的聚类算法大部分都是针对n维的,针对一维数据的聚类方式较少,今天就来学习下如何给一维的数据进行聚类。 方案一:采用K-Means对一维数据聚类 Python代码如下: from sklearn.cluster im…...

100多种视频转场素材|专业胶片,抖动,光效电影转场特效PR效果预设
100多种 Premiere Pro 效果预设,包含:“胶片框架”、“胶片烧录”、“彩色LUT”、“相机抖动”、“电影Vignette”和“胶片颗粒”。非常适合制作复古风格的视频,添加独特的色彩。包括视频教程。 来自PR模板网:https://prmuban.com…...

http与apache
目录 1.http相关概念 2.http请求的完整过程 3.访问浏览器背后的原理过程 4.动态页面与静态页面区别 静态页面: 动态页面: 5.http协议版本 6.http请求方法 7.HTTP协议报文格式 8.http响应状态码 1xx:提示信息 2xx:成功…...
一、服务器准备
本案例使用VMware Workstation Pro虚拟机创建虚拟服务器来搭建Linux服务器集群,所用软件及版本如下: Centos7.7-64bit 1、三台虚拟机创建 第一种方式:通过iso镜像文件来进行安装(不推荐) 第二种方式:直接复制安装好的虚拟机文…...

区块链optimism主网节点搭建
文章目录 官方参考资料编译环境搭建编译Optimism Monorepo编译op-geth 执行下载数据快照生成op-geth和op-node通信密钥op-geth执行脚本 op-node执行脚本 启动日志op-gethop-node 本文是按照官方参考资料基于源码的方式成功搭建optimism主网节点。 官方参考资料 源码࿱…...
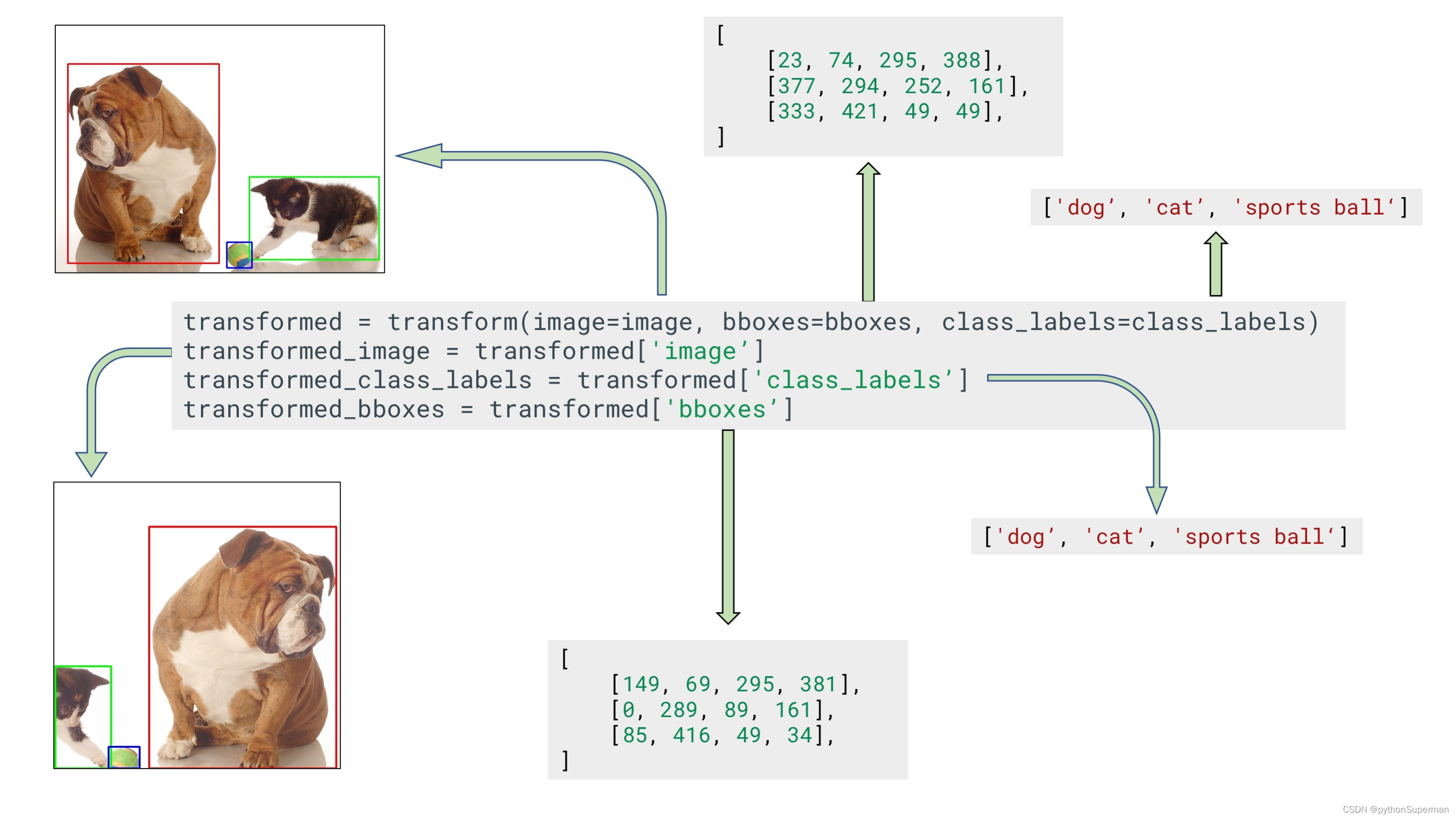
Bounding boxes augmentation for object detection
Different annotations formats Bounding boxes are rectangles that mark objects on an image. There are multiple formats of bounding boxes annotations. Each format uses its specific representation of bouning boxes coordinates 每种格式都使用其特定的边界框坐标…...
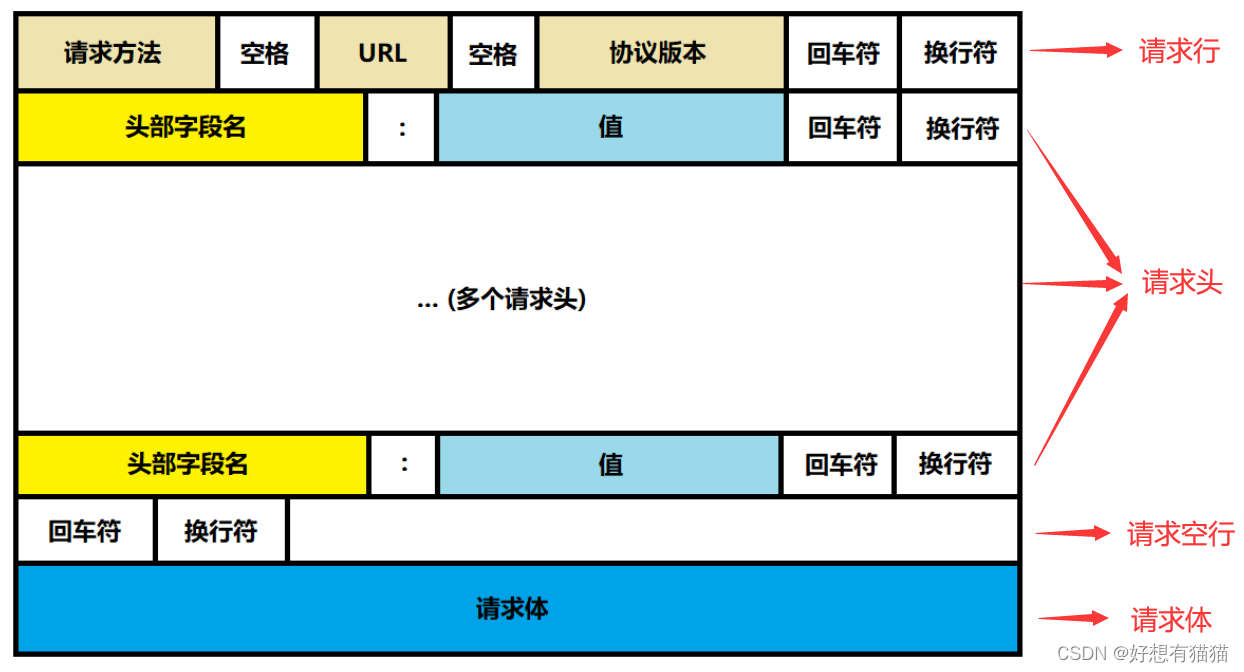
【计算机网络学习之路】HTTP请求
目录 前言 HTTP请求报文格式 一. 请求行 HTTP请求方法 GET和POST的区别 URL 二. 请求头 常见的Header 常见的额请求体数据类型 三. 请求体 结束语 前言 HTTP是应用层的一个协议。实际我们访问一个网页,都会像该网页的服务器发送HTTP请求,服务…...

java之字符串常用处理函数
在Java中,你可以使用Collections.sort()方法对字符串中的字符进行排序。这个方法会按照字母顺序对字符进行排序。 以下是一个例子: import java.util.Arrays; import java.util.Collections; public class Main { public static void main(…...

【XILINX】ERROR:Place:1136 - This design contains a global buffer instance
记录一个ISE软件使用过程中遇到的问题及解决方案。 芯片:spartan6 问题 ERROR:Place:1136 - This design contains a global buffer instance, , driving the net,>, that is driving the following (first 30) non-clock load pins. This is not a recommended…...
【文件上传系列】No.0 利用 FormData 实现文件上传、监控网路速度和上传进度(原生前端,Koa 后端)
利用 FormData 实现文件上传 基础功能:上传文件 演示如下: 概括流程: 前端:把文件数据获取并 append 到 FormData 对象中后端:通过 ctx.request.files 对象拿到二进制数据,获得 node 暂存的文件路径 前端…...

web前端之JavaScrip的笔试题
MENU Promise笔试题-02prototype和__proto__的笔试题JavaScript引用类型值值操和运算符优先级比较--笔试原型与原型链--笔试-05作用域-笔试事件队列-笔试题JavaScript之变量提升-笔试题JavaScript之原型链--笔试题 Promise笔试题-02 console.log(1); // 宏仁务 2 setTimeout(_…...

生活、工作常用API免费接口
身份证识别OCR:传入身份证照片,识别照片文字信息并返回,包括姓名、身份证号码、性别、民族、出生年月日、地址、签发机关及有效期。二维码识别OCR:对图片中的二维码、条形码进行检测和识别,返回存储的文字内容。银行卡…...

PHP使用mkcert本地开发生成HTTPS证书 PhpEnv集成环境
PHP使用mkcert本地开发生成HTTPS证书 PhpEnv集成环境 前言一、介绍 mkcert二、安装/使用 mkcert1. 安装2. 使用 总结 前言 本地开发时有些功能只有在 https 证书的情况下才能使用, 例如一些 Web API 一、介绍 mkcert Github地址 mkcert 是一个制作本地可信开发证书的简单工具。…...
DHTMLX Scheduler PRO 6.0.5 Crack
功能丰富的 JavaScript调度程序 DHTMLX Scheduler 是一个 JavaScript 日程安排日历,具有 10 个视图和可定制的界面,用于开发任何类型的日程安排应用程序。 DHTMLX JS 调度程序库的主要特性 我们的 JS 调度程序最需要的功能之一是时间轴视图。借助时间轴…...

AddressSanitizer和LeakSanitizer有什么区别
AddressSanitizer(ASan)和LeakSanitizer(LSan)都是用于内存错误检测的工具,它们的主要区别在于检测的问题类型和应用场景。 AddressSanitizer(ASan): ASan是一种用于检测内存错误的工具…...
-CoreDNS+ETCD实现DNS服务发现)
CoreDNS实战(二)-CoreDNS+ETCD实现DNS服务发现
1 引言 在前面的文章中讲了如何搭建一个内网的DNS服务,但是这里有个问题,mxsm-register.local表示局域网的注册中心域名,如果需要将每台部署了注册中心的IP地址写到CoreDNS的配置文件中。这样就需要每次都去修改 Corefile 配置文件。那有没有…...

B站缓存视频M4S合并MP4(js + ffmpeg )
文章目录 B站缓存视频转MP4(js ffmpeg )1、说明 2、ffmpeg2.1 下载地址2.2 配置环境变量2.3 测试2.4 转换MP4命令 3、处理程序 B站缓存视频转MP4(js ffmpeg ) 注意:这样的方式只用于个人之间不同设备的离线观看。请…...
学习IO的第四天
作业 : 使用两个子进程完成两个文件的拷贝,子进程1拷贝前一半内容,子进程2拷贝后一般内容,父进程用于回收两个子进程的资源 #include <head.h>int main(int argc, const char *argv[]) {int rd -1;if((rdopen("./01_test.c&quo…...
Linux:缓冲区的概念理解
文章目录 缓冲区什么是缓冲区?缓冲区的意义是什么?缓冲区的刷新方式 理解缓冲区用户缓冲区和内核缓冲区缓冲区在哪里? 本篇主要总结的是关于缓冲区的概念理解,以及再次基础上对文件的常用接口进行一定程度的封装 缓冲区 什么是缓…...

中山大学李华山、王彪课题组开发 SEN 机器学习模型,高精度预测材料性能
内容一览:了解全局晶体对称性并分析等变信息,对于预测材料性能至关重要,但现有的、基于卷积网络的算法尚且无法完全实现这些需求。针对于此,中山大学的李华山、王彪课题组,开发了一款名为 SEN 的机器学习模型ÿ…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...
