LeetCode435. Non-overlapping Intervals
文章目录
- 一、题目
- 二、题解
一、题目
Given an array of intervals intervals where intervals[i] = [starti, endi], return the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.
Example 1:
Input: intervals = [[1,2],[2,3],[3,4],[1,3]]
Output: 1
Explanation: [1,3] can be removed and the rest of the intervals are non-overlapping.
Example 2:
Input: intervals = [[1,2],[1,2],[1,2]]
Output: 2
Explanation: You need to remove two [1,2] to make the rest of the intervals non-overlapping.
Example 3:
Input: intervals = [[1,2],[2,3]]
Output: 0
Explanation: You don’t need to remove any of the intervals since they’re already non-overlapping.
Constraints:
1 <= intervals.length <= 105
intervals[i].length == 2
-5 * 104 <= starti < endi <= 5 * 104
二、题解
class Solution {
public:static bool cmp(vector<int>& a,vector<int>& b){return a[0] < b[0];}int eraseOverlapIntervals(vector<vector<int>>& intervals) {sort(intervals.begin(),intervals.end(),cmp);int res = 0;for(int i = 1;i < intervals.size();i++){if(intervals[i][0] < intervals[i-1][1]){res++;intervals[i][1] = min(intervals[i-1][1],intervals[i][1]);}}return res;}
};
相关文章:

LeetCode435. Non-overlapping Intervals
文章目录 一、题目二、题解 一、题目 Given an array of intervals intervals where intervals[i] [starti, endi], return the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping. Example 1: Input: intervals [[1,2]…...

ffmpeg 实现多视频轨录制到同一个文件
引言 在视频录制中,有时会碰到这样一个需求,将不同摄像头的画面写入到一个视频文件,这个叫法很多,有的厂家叫合流模式,有的叫多画面多流模式。无论如何,它们的实质都是在一个视频文件上实现多路不同分辨率视…...

vue3中子组件调用父组件的方法
<script lang"ts" setup>前提 父组件: 子组件: const emit defineEmits([closeson]) 在子组件的方法中使用: emit(closeson)...

使用OkHttp上传本地图片及参数
下面以一个例子来讲解在项目中如何使用OKHttp来对本地图片做个最简单的上传功能,基本上无封装,只需要简单调用便可(对于OKHttp的引入不再单独做介绍)。 1:构建上传图片附带的参数(params) Map…...
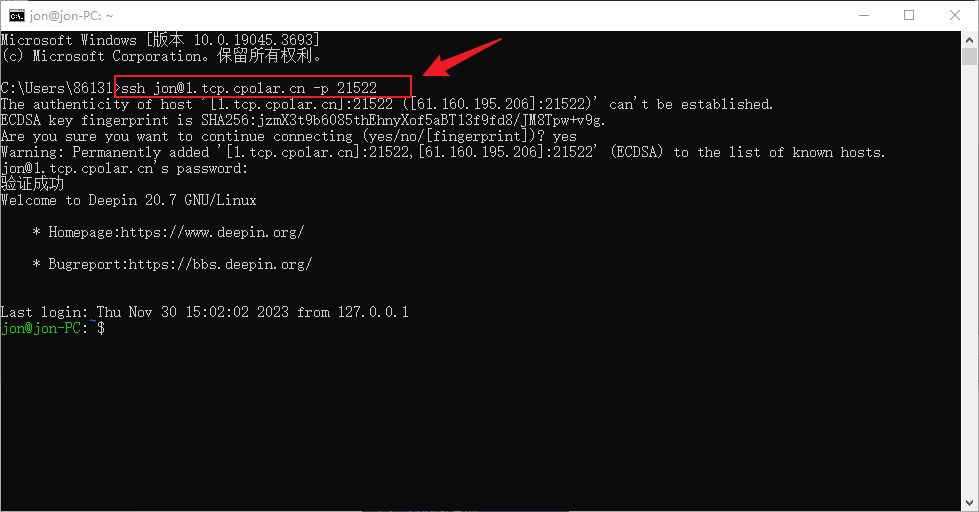
无公网IP环境如何SSH远程连接Deepin操作系统
文章目录 前言1. 开启SSH服务2. Deppin安装Cpolar3. 配置ssh公网地址4. 公网远程SSH连接5. 固定连接SSH公网地址6. SSH固定地址连接测试 前言 Deepin操作系统是一个基于Debian的Linux操作系统,专注于使用者对日常办公、学习、生活和娱乐的操作体验的极致࿰…...

不会代码(零基础)学语音开发(语音控制板载双继电器)
继电器的用途可广了,这个语音控制用处也特别广。继电器,它实际上是一种“自动开关”,用小电流去控制大电流运作,在电路中起着自动调节、安全保护、转换电路等作用。 在日常生活中,你插入汽车钥匙,车辆可以…...
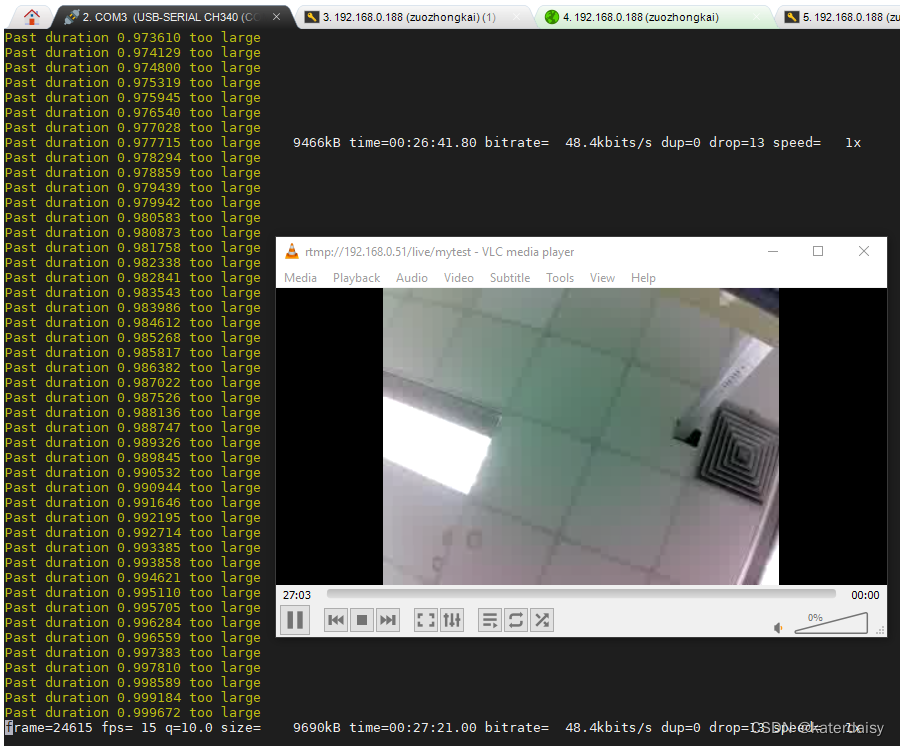
在imx6ull中加入ov5640模块
本来觉得是一件很简单的事情但是走了很多的弯路,记录一下调试过程。 先使用正点原子提供的出厂内核把摄像头影像调试出来,然后cat /dev/video1,看一下video1牵扯到哪些模块,可以看到需要ov5640_camera.ko和 mx6s_capture.ko这两个…...
Kafka中的auto-offset-reset配置
Kafka这个服务在启动时会依赖于Zookeeper,Kafka相关的部分数据也会存储在Zookeeper中。如果kafka或者Zookeeper中存在脏数据的话(即错误数据),这个时候虽然生产者可以正常生产消息,但是消费者会出现无法正常消费消息的…...

TCP/IP_整理起因
先分享一个初级的问题;有个客户现场,终端设备使用客户网络更新很慢,使用手机热点更新速度符合预期;网络部署情况如下: 前期花费了很大的精力进行问题排查对比,怀疑是客户网络问题(其他的客户现…...

CG-0A 电子水尺水导电测量原理应用于道路积水监测
CG-0A 电子水尺水导电测量原理应用于道路积水监测产品概述 本产品是一种采用微处理器芯片为控制器,内置通讯电路的数字式水位传感器,具备高的可靠性及抗干扰性能。适用于江、河、湖、水库及蓄水池、水渠等处的水位测量使用。 本产品采用了生产工艺技术…...

openEuler JDK21 部署 Zookeeper 集群
zookeeper-jdk21 操作系统:openEuler JDK:21 主机名IP地址spark01192.168.171.101spark02192.168.171.102spark03192.168.171.103 安装 1. 升级内核和软件 yum -y update2. 安装常用软件 yum -y install gcc gcc-c autoconf automake cmake make \zl…...

前端——html拖拽原理
文章目录 ⭐前言⭐draggable属性💖 api💖 单向拖动示例💖 双向拖动示例 ⭐总结⭐结束 ⭐前言 大家好,我是yma16,本文分享关于 前端——html拖拽原理。 vue3系列相关文章: vue3 fastapi 实现选择目录所有文…...
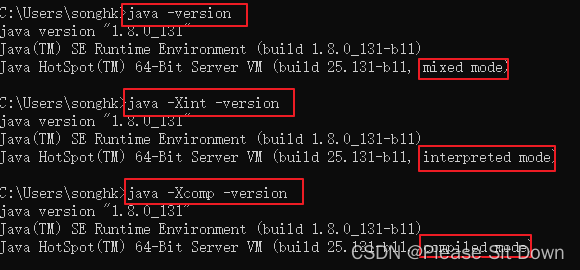
JVM 执行引擎篇
机器码、指令、汇编语言 机器码 各种用二进制编码方式表示的指令,叫做机器指令码。开始,人们就用它采编写程序,这就是机器语言。机器语言虽然能够被计算机理解和接受,但和人们的语言差别太大,不易被人们理解和记忆&a…...

js中数组对象去重的方法
前端面试题库 (面试必备) 推荐:★★★★★ 地址:前端面试题库 最近工作中需要用到数组对象去重的方法,我是怎么想也没想出来,今天稍微研究了一下,总算找到了2种方法。分享一下&…...

【送书活动四期】被GitHub 要求强制开启 2FA 双重身份验证,我该怎么办?
记得是因为fork了OpenZeppelin/openzeppelin-contracts的项目,之后就被GitHub 要求强制开启 2FA 双重身份验证了,一拖再拖,再过几天帐户操作将受到限制了,只能去搞一下了 目录 2FA是什么为什么要开启 2FA 验证GitHub 欲在整个平台…...
)
GO设计模式——13、享元模式(结构型)
目录 享元模式(Flyweight Pattern) 享元模式的核心角色: 优缺点 使用场景 注意事项 代码实现 享元模式(Flyweight Pattern) 享元模式(Flyweight Pattern)它通过共享对象来减少内存使用和提…...
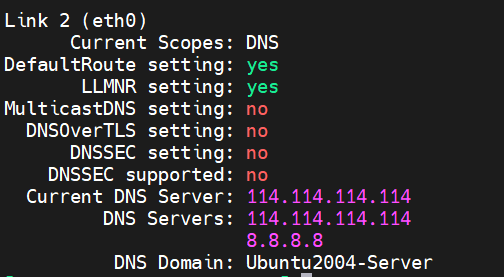
Linux 网络协议
1 网络基础 1.1 网络概念 网络是一组计算机或者网络设备通过有形的线缆或者无形的媒介如无线,连接起来,按照一定的规则,进行通讯的集合( 缺一不可 )。 5G的来临以及IPv6的不断普及,能够进行联网的设备将会是越来越多(…...
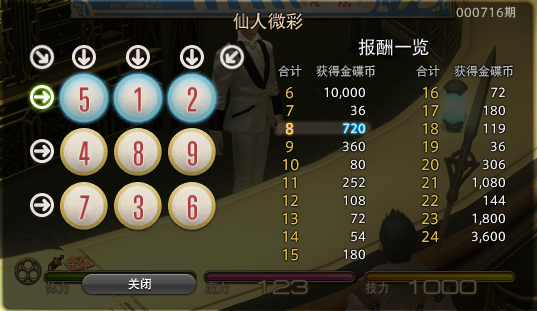
【C语言】7-32 刮刮彩票 分数 20
7-32 刮刮彩票 分数 20 全屏浏览题目 切换布局 作者 DAI, Longao 单位 杭州百腾教育科技有限公司 “刮刮彩票”是一款网络游戏里面的一个小游戏。如图所示: 每次游戏玩家会拿到一张彩票,上面会有 9 个数字,分别为数字 1 到数字 9…...
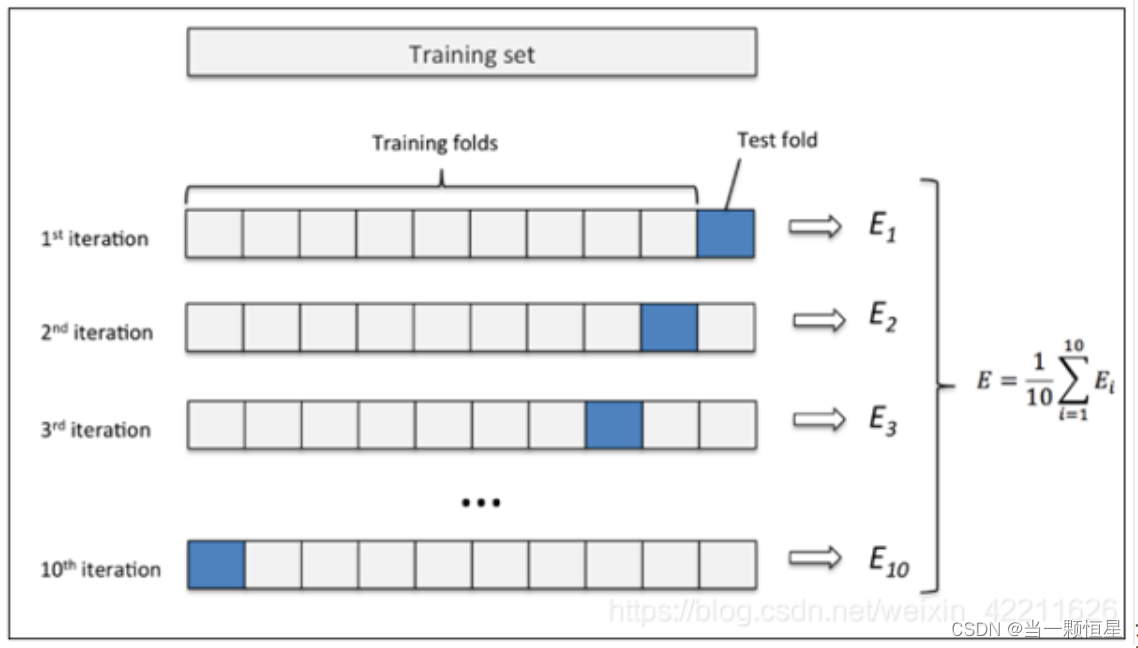
交叉验证以及scikit-learn实现
交叉验证 交叉验证既可以解决数据集的数据量不够大问题,也可以解决参数调优的问题。 主要有三种方式: 简单交叉验证(HoldOut检验)、k折交叉验证(k-fold交叉验证)、自助法。 本文仅针对k折交叉验证做详细解…...

css实现头部占一定高度,内容区占剩余高度可滚动
上下布局: <div class"container"><header class"header">头部内容</header><div class"content">内容区域</div> </div>.container {display: flex;flex-direction: column;height: 100vh; /*…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
