excel做预测的方法集合
一. LINEST函数
首先,一元线性回归的方程:
y = a + bx
相应的,多元线性回归方程式:
y = a + b1x1 + b2x2 + … + bnxn
这里:
- y - 因变量即预测值
- x - 自变量
- a - 截距
- b - 斜率
LINEST的可以返回回归方程的 截距(a) 和 斜率(b) 和其他回归统计值。
(1)LINEST 函数语法
LINEST(known_y's, [known_x's], [const], [stats])
- known_y's (必须) 因变量,单行/单列
- known_x's (必须) 自变量,单行/单列
- const(可选) :
- TRUE[默认]:正常计算截距 a
- FALSE:强制截距 a = 0,此时回归方程 y = bx
- stats(可选) :
- TRUE:返回统计值
- FALSE[默认]:不返回统计值,只返回斜率和截距
注意 LINEST 函数返回值为数组,需要使用数组三键 CTRL + SHIFT + ENTER
使用SLOPE得到的斜率结果与LINEST 函数是一样的
(2)LINEST 返回的回归统计值
当LINEST函数参数 stats = TRUE,此时返回值包含统计值:

如果回归模型为多元线性方程: 
LINEST函数返回值顺序:

最后三行,从第三列开始返回值为#NA,可以通过 IFERROR 函数进行嵌套以消除
二. LINEST 使用举例
(1)一元线性回归: 
【例1】广告投入与雨伞的销量

这里:
- Advertising 是自变量 x (B2:B13),Umbrellas sold 是因变量 y (C2:C13)
- 选中单元格 E2:F2 输入 = LINEST(C2:C13, B2:B13),
CTRL + SHIFT + ENTER - 这里 0.526 是斜率,-4.994 是截距
- 回归方程为: y=−4.994+0.526∗x
- 预测:如果投入广告为 $50,预测雨伞的销量为:
-4.994 + 0.526*50 = 21.3
a)通过函数获取回归方程斜率
=SLOPE(C2:C13,B2:B13)
=INDEX(LINEST(C2:C13,B2:B13),1)
LINEST (C2:C13,B2:B13) 返回值为 1 行 2 列的数组
b)通过函数获取回归方程截距
=INTERCEPT(C2:C13,B2:B13)
=INDEX(LINEST(C2:C13,B2:B13),2)
函数对比:

(2)2. 多元线性回归: 
【例2】广告投入,下雨量与雨伞的销量

如果存在两个或更多的自变量 ,�1,�2... ,那么这些自变量必须位于相邻列,整体作为 LINEST 函数 的参数 known_x's .
注意,对于多元线性回归, LINEST函数以逆序的形式返回的 「斜率」,从右往左分别为
对于例2:
- Rainfall 是自变量 X1 (B2:B13),Advertising 是自变量 X2 (C2:C13),Umbrellas sold 是因变量 y (D2:D13)。
- 选中单元格 F2:H2 输入 = LINEST(D2:D13, B2:C13),
CTRL + SHIFT + ENTER - 这里 0.309 是斜率 b2 ,0.186 是斜率 b1 ,-10.739是截距
- 回归方程为: y=−10.739+0.186x1+0.309x2
- 预测:如果投入广告为 $50,当月平均降雨量为 100 mm,预测雨伞的销量为:-10.739 + 0.186 * 100 + 0.309 *50 = 23.31
(3)使用LINEST 函数进行一元线性回归预测
在一元线性回归的应用中,LINEST 除了可以直接返回 斜率 b 以及截距 a 之外,通过结合函数SUM / SUMPRODUCT 可以实现给定自变量 (X) 预测因变量 (y)。
回到例1, 当10月(Oct) 广告支出为 $50,此时预测雨伞销量为:
= SUM(LINEST(C2:C10, B2:B10)*{50,1})

实际应用时,对于给定的自变量(x) ,一般放在单元格中,同时相邻单元格输入 1。
例如,下图 E2 输入自变量 x,F2 输入常量 1,单元格 G2 代表计算的预测值 y,通过:
- SUMPRODUCT (使用
ENTER)
= SUMPRODUCT(LINEST(C2:C10, B2:B10)*(E2:F2))
- SUM(使用
CTRL + SHIFT + ENTER)
= SUM(LINEST(C2:C10, B2:B10)*(E2:F2))

(4) 使用LINEST 函数进行多元线性回归预测
同样在多元线性回归的应用中,LINEST 也可以结合函数SUM / SUMPRODUCT 可以实现给定多个自变量 ( X1,X2... ) 预测因变量 (y)。
回到例2, 当广告支出为 $50 ( X2 ),下雨量为100 ( X1),此时预测雨伞的销量为:
= SUM(LINEST(D2:D10, B2:C10)*{50,100,1})

注意,对于多元线性回归, LINEST函数以逆序的形式返回的 「斜率」,从右往左分别为。因此在如上函数中常数数组顺序为{50,100,1} 分别代表

实际应用时,对于给定的多个自变量(x) ,放在相邻单元格中,同时最后单元格输入 1。
例如,下图 F2 输入自变量 X2 ,G2 输入自变量 X1 ,H2 输入常量 1,单元格 I2 代表计算的预测值 y,通过:
- SUMPRODUCT (使用
ENTER)
= SUMPRODUCT(LINEST(C2:C10, B2:B10)(F2:H2))
- SUM (使用
CTRL + SHIFT + ENTER)
= SUM(LINEST(C2:C10, B2:B10)(F2:H2))

(5)使用LINEST 进行线性回归的统计值
前面关于LINEST函数的语法中,只要参数 stats = TRUE 函数会返回回归统计值。
对于例2, 若要返回回归统计值:
= LINEST(D2:D13, B2:C13, TRUE, TRUE)
这里列 B 和列 C 分别代表两个自变量,因此选择 3 行(2个斜率一个截距) 5 列的区域 [F2:H6],同时输入如上公式

对于LINEST返回值包含 #NA 错误,可以使用嵌套 IFERROR 函数,如下: = IFERROR(LINEST(D2:D13, B2:C13, TRUE, TRUE), "")
下图解释了LINEST函数返回统计值的含义:

简单介绍除斜率和截距外的其他返回值:

三. 5 个关于LINEST函数的知识点

四. LINEST 函数报错处理
- LINEST 返回值只有斜率值,此时应检查公式是否为数组公式输,即是否使用 CTRL + SHIFT + ENTER 输入
- REF!错误,检查参数 known_x's 和参数 known_y's 是否大小一致
- VALUE 错误
- 检查 参数 known_x's 和参数 known_y's 是否包含空单元格,文本值,文本型数值
- 检查参数 const 或 stat 输入值非 FALSE / TRUE
相关文章:

excel做预测的方法集合
一. LINEST函数 首先,一元线性回归的方程: y a bx 相应的,多元线性回归方程式: y a b1x1 b2x2 … bnxn 这里: y - 因变量即预测值x - 自变量a - 截距b - 斜率 LINEST的可以返回回归方程的 截距(a) 和 斜…...
12月8日作业
使用手动连接,将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中,在自定义的槽函数中调用关闭函数;将登录按钮使用qt5版本的连接到自定义的槽函数中,在槽函数中判断u界面上输入的账号是否为"admin",…...

RefCell 数据类型
内部可变性(interior mutability)是RUST的设计模式之一,它允许你在只持有不可变引用的前提下对数据进行修改。为了能改变数据,内部可变性模式在它的数据结构中使用了unsafe(不安全)代码来绕过RUST正常的可变…...

[oeasy]python0002_终端_CLI_GUI_编程环境_游戏_真实_元宇宙
回忆 上次 了解了 python 语言的特点 历史悠久功能强大深受好评已成趋势 3大主流操作系统 macwindowslinux 我们 选择 linux 作为基础系统 为什么选择 黑乎乎的命令行界面呢?🤔 GUI vs CLI 个人电脑 用图标和菜单组成 图形界面(GUI) Graphic User I…...
微服务1 springcloud学习笔记P1-P40
b微服务技术栈_哔哩哔哩_bilibili 文档资料: 链接:https://pan.baidu.com/s/1P_Ag1BYiPaF52EI19A0YRw?pwdd03r 提取码:d03r 一 了解微服务技术 二 Eureka (1) Eureka配置 (2) 注册user-service (3) 总结 Ribbon 负载均衡 (1) 流程 三 nacos配置管理…...
【页面】表格展示
展示 Dom <template><div class"srch-result-container"><!--左侧--><div class"left"><div v-for"(item,index) in muneList" :key"index" :class"(muneIndexitem.mm)?active:"click"pa…...
-综合练习题-10道经典题目)
天池SQL训练营(六)-综合练习题-10道经典题目
如果你还没有学习过SQL训练营的以下知识,请查阅主页博文学习: Task 1 SQL基础:初识数据库与SQL-安装与基本介绍等 Task 2 SQL基础:查询与排序-select、运算符、聚合分组查询等 Task 3 SQL进阶:复杂查询方法-视图、子查…...

某校园报名sign解密
某校园报名sign解密 定位 看了下确实是md5标准算法,接下来就看下加密的明文了 最后分开看了下, sign md5(用户名 活动id 10位时间戳 keys)...

2024年安防视频监控行业将面临4大机遇和挑战
当前安防监控市场处于快速发展的阶段,市场不仅有传统的视频监控、门禁系统等单一功能的设备,还涌现出了一系列集成多种安防功能的综合系统。随着人工智能技术的发展,安防监控设备不仅可以对场所进行实时监控,还可以通过图像识别、…...

搞懂HashTable, HashMap, ConcurrentHashMap 的区别,看着一篇就足够了!!!
🛩️🛩️🛩️ 今天给大家分享的是 HashTable, HashMap, ConcurrentHashMap之间的区别,也是自己学习过程中的总结。 清风的CSDN博客 🛩️🛩️🛩️希望我的文章能对你有所帮助,有不足的…...

PostgreSQL 技术内幕(十二) CloudberryDB 并行化查询之路
随着数据驱动的应用日益增多,数据查询和分析的量级和时效性要求也在不断提升,对数据库的查询性能提出了更高的要求。为了满足这一需求,数据库引擎不断经历创新,其中并行执行引擎是性能提升的重要手段之一,逐渐成为数据…...

Vue学习计划-Vue2--Vue核心(七)生命周期
抛出问题:一进入页面就开启一个定时器,每隔1秒count就加1,如何实现 示例: <body> <div id"app">{{ n }}<button click"add">执行</button> </div><script>let vm new …...
———HBuilder的下载与使用(详细步骤))
前端知识笔记(三十四)———HBuilder的下载与使用(详细步骤)
一、HBuilder IDE的下载 HBuilder下载官网地址: 在地址栏中直接输入https://www.dcloud.io 或者直接点击下面的链接 DCloud - HBuilder、HBuilderX、uni-app、uniapp、5、5plus、mui、wap2app、流应用、HTML5、小程序开发、跨平台App、多端框架 进入官网&#x…...

stl容器
大部分容器的size的复杂度如下: std::vector: 时间复杂度为(1). std::deque: 时间复杂度为 O(1). 双端队列 std::list: 时间复杂度为 O(1)(C11 及以后的版本)。 std::forward_list: 时间复…...
android https 证书过期
有的时候 我们android https 证书过期 ,或者使用明文等方式去访问服务器 可能会碰到类似的 问题 : javax.net.ssl.SSLHandshakeException: Chain validation failed java.security.cert.CertPathValidatorException: Response is unreliable: its validi…...
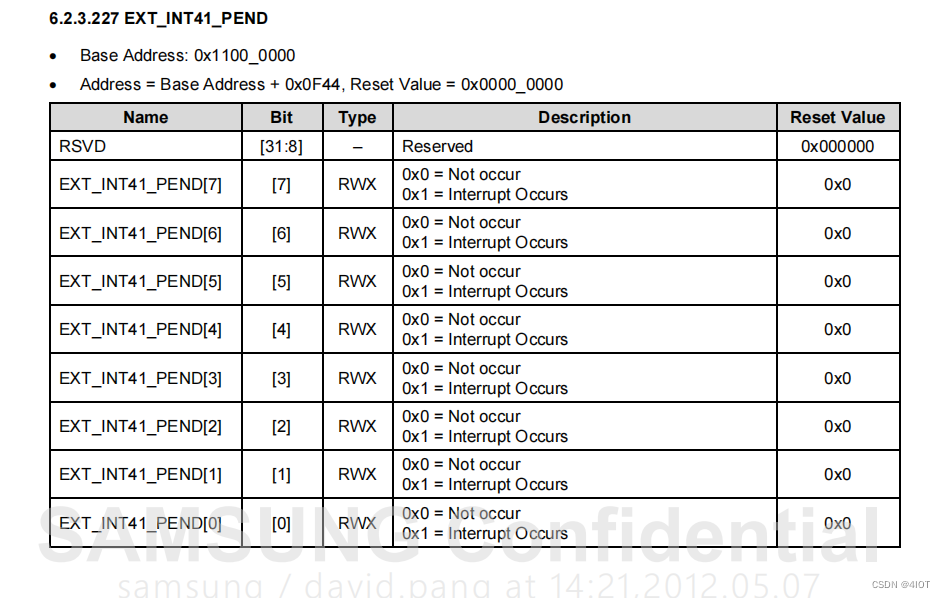
lv11 嵌入式开发 中断控制器14
目录 1 中断控制器 编辑 2 Exynos4412下的中断控制器 2.1 概述 2.2 特征 编辑 2.3 中断状态 2.4 中断类型 2.5 中断控制器GIC中断表 3 中断控制器寄存器详解 3.1 ICDDCR(Interrupt Controller Distributor Control Register) 3.2 ICDISER…...

IDEA 出现问题:Idea-操作多次commit,如何合并为一个并push解决方案
❤️作者主页:小虚竹 ❤️作者简介:大家好,我是小虚竹。2022年度博客之星评选TOP 10🏆,Java领域优质创作者🏆,CSDN博客专家🏆,华为云享专家🏆,掘金年度人气作…...
)
贝蒂的捣蛋小游戏~(C语言)
引言: 前面贝蒂已经给大家介绍了选择,循环结构~,今天贝蒂就基于这两种结构,为大家讲解一种捣蛋小游戏的设计思路和方法哦。 1.游戏要求 游戏要求: 1. 电脑⾃动⽣成1~100的随机数 2. 玩家猜数字,猜数字的过…...

c# 判断是否连接公网
有一个需求,软件需要在连接公网的状态下才能使用,否则弹出提示 我们判断一下网络不通情况 1.系统未开启网络:例如关掉了WIFI,拔掉网线 2.网络已连接无internet:连接了路由器,但路由器未连接外网 对于以上…...
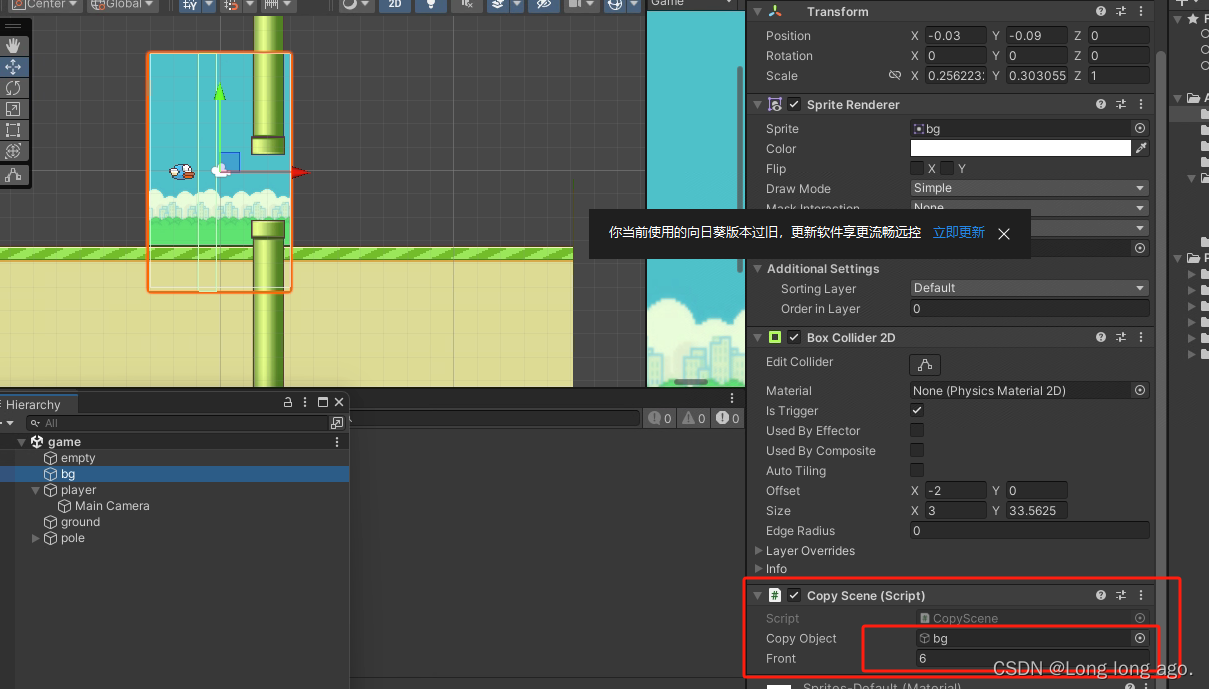
unity 2d 入门 飞翔小鸟 场景延续(八)
1、新建c#脚本如下 代码,在前方生成生成自身图片并3s后销毁自身,在碰撞物体后小鸟死亡后不删除自身 using System.Collections; using System.Collections.Generic; using UnityEngine;public class CopyScene : MonoBehaviour { //要复制的对象public…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
