蛮力法最大值连续子序问题
概念:
在一个给定的整数数组中找到一个连续的子序列,使得子序列的元素之和最大
思路:
-
遍历所有可能的子序列,计算它们的和。
-
在每次计算过程中,记录当前最大的子序列和。
-
返回最大的子序列和作为结果。
代码:
#include <iostream>
#include <climits>// 计算给定数组的最大连续子序列之和
int maxSubarraySum(int arr[], int size) {int maxSum = INT_MIN; // 最大和初始化为整型最小值// 遍历所有可能的子序列for (int i = 0; i < size; i++) {int currentSum = 0;for (int j = i; j < size; j++) {currentSum += arr[j]; // 将当前元素添加到当前子序列和中if (currentSum > maxSum) {maxSum = currentSum; // 更新最大和}}}return maxSum; // 返回最大和
}int main() {int arr[] = {-2, -3, 4, -1, -2, 1, 5, -3};int size = sizeof(arr) / sizeof(arr[0]); // 计算数组大小int maxSum = maxSubarraySum(arr, size); // 调用函数计算最大和std::cout << "Maximum sum of a subarray: " << maxSum << std::endl; // 输出结果return 0;
}
相关文章:

蛮力法最大值连续子序问题
概念: 在一个给定的整数数组中找到一个连续的子序列,使得子序列的元素之和最大 思路: 遍历所有可能的子序列,计算它们的和。 在每次计算过程中,记录当前最大的子序列和。 返回最大的子序列和作为结果。 代码: #include <iostream> #…...

多功能智能遥测终端机 5G/4G+北斗多信道 视频采集传输
计讯物联多功能智能遥测终端机,全网通5G/4G无线通信、弱信号地区北斗通信,多信道自动切换保障通信联通,丰富网络接口及行业应用接口,支持水利、环保、工业传感器、控制终端、智能终端接入,模拟量/数字量/信号量采集&am…...
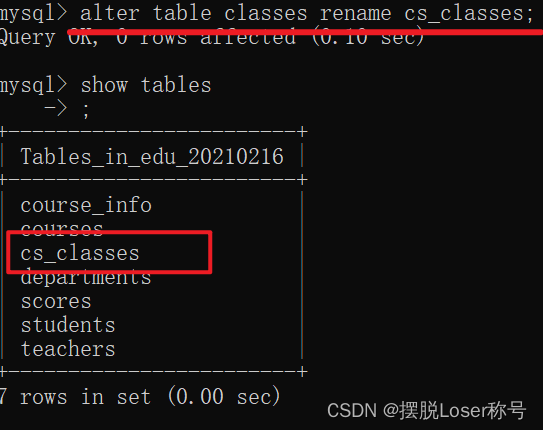
1.查看表的基本结构,表的详细结构和修改表名
查看表的基本结构,表的详细结构和修改表名 1.查看数据表基本结构 有强迫症或健忘症的小伙伴们在建好数据库和表以后,通常会怀疑自己刚才是不是敲错了,怎么办?如果不是使用图形界面是不是就没法查看啦? 不存在的,这就…...

Mybatis实用教程之XML实现动态sql
系列文章目录 1、mybatis简介及数据库连接池 2、mybatis中selectOne的使用 3、mybatis简单使用 4、mybatis中resultMap结果集的使用 Mybatis实用教程之XML实现动态sql 系列文章目录前言1. 动态条件查询2. 动态更新语句3. 动态插入语句4、其他标签的使用 前言 当编写 MyBatis 中…...
)
混合App开发实现页面跳转(更新中)
util.js /*** 这个函数被用来获取 URL 中的查询参数,并将它们以对象(键值对)的形式返回* param {string} url* returns {object} oParams*/ export function getUrlQuery(url null) {let sUrl url || window.location.href;let oParams {…...

【FPGA】Verilog:BCD 加法器的实现
0x00 XOR 运算在 2 的补码加减法中的应用 2 的补码加减法的特点是,当从某个数中减去负数时,将其转换为正数的加法来计算,并将减去正数的情况转换为负数的加法来计算,从而将所有减法运算转换为加法运算。在这种情况下,…...
机器学习第15天:GBDT模型
☁️主页 Nowl 🔥专栏《机器学习实战》 《机器学习》 📑君子坐而论道,少年起而行之 文章目录 GBDT模型介绍 Boosting 残差 GBDT的缺点 python代码实现 代码 模型参数解释 结语 GBDT模型介绍 GBDT(Gradient Boos…...

STM32F407-14.3.9-01输出比较模式
输出比较模式 此功能用于控制输出波形,或指示已经过某一时间段。 当捕获/比较寄存器与计数器之间相匹配时,输出比较功能: ● 将为相应的输出引脚分配一个可编程值,该值由输出比较模式(TIMx_CCMRx 寄存器中的 OCxM⑦…...
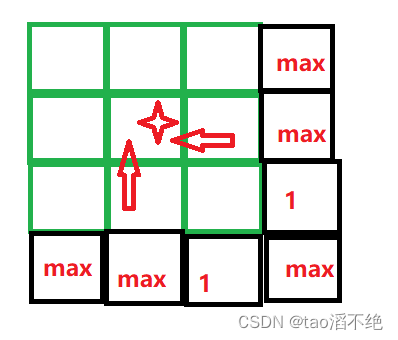
LeetCode题:174. 地下城游戏
目录 一、题目要求 二、解题思路 (1)状态表示 (2)状态转移方程 (3)初始化dp表 (4)填表顺序 (5)返回值 三、代码 一、题目要求 174. 地下城游戏 恶魔们…...
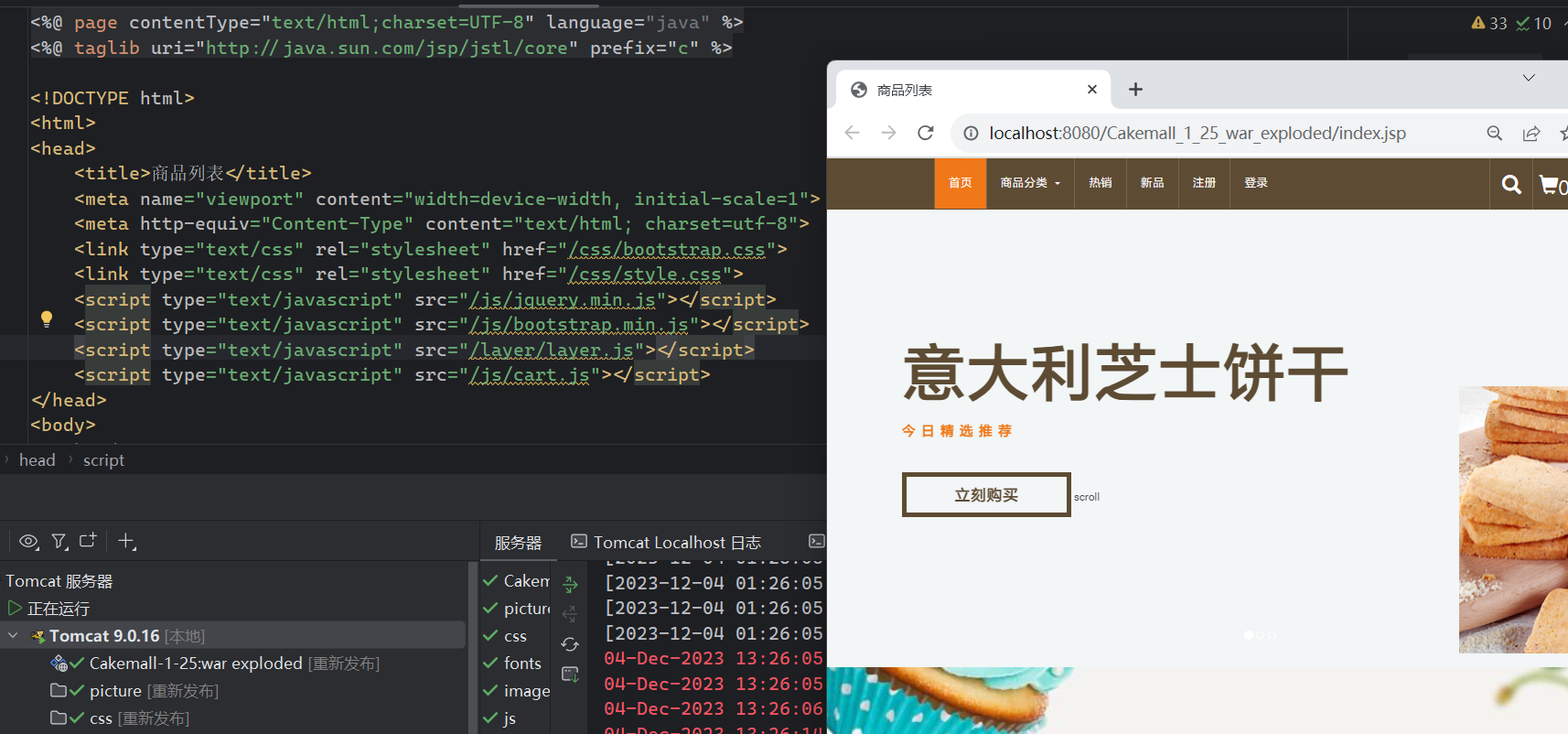
CSS、JS文件无法正确加载至页面问题与解决
目录 1. 问题出现 2. 分析与解决 3. 总结 1. 问题出现 自己在写项目是时候,想启动浏览器查询首页面index.jsp的显示效果 预期效果应该是下面这样的: 但是实际上是这样的: 意思也就是说可能是关于CSS、JS相关的引入方面出了问题ÿ…...
ftp的服务安装配置
安装 yum install -y vsftpd # 是否安装成功 rpm -qa | grep vsftpd # 是否开机启动 systemctl list-unit-files | grep vsftpd # 开机启动 systemctl enable vsftpd.service # ftp端口 netstat -antup | grep ftp # 状态 service vsftpd status service vsftpd start service…...
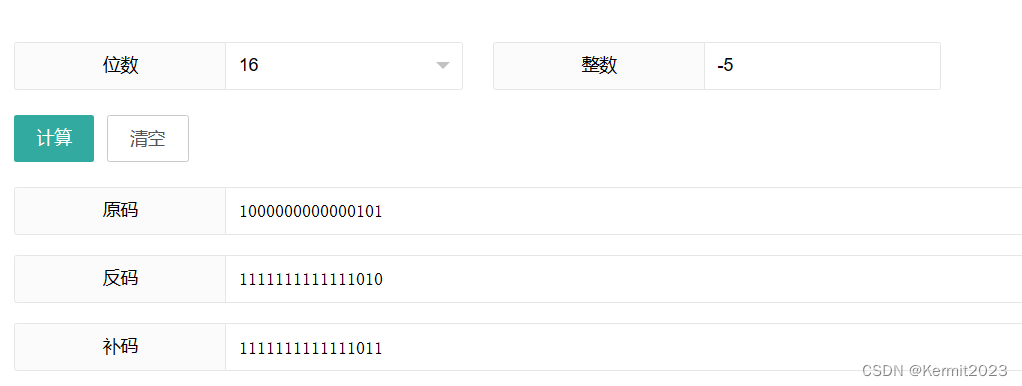
原码,补码,反码(极简版)
原码补码反码 都有符号位,0表示正数,1表示负数 正数 正数的原码,补码,反码都相同 负数 负数的原码,最高位是1,其余的用正常二进制表示 负数的反码,对原码进行符号位不变,其余位…...

uniapp监听wifi连接状态
在uniapp中检测WiFi连接状态可以使用uni的API进行操作。 uni.onNetworkStatusChange((res) > { console.log(res)uni.getConnectedWifi({success: function(res) {console.log(已连接WIFI, res);},fail: function(err) {console.log(未连接WIFI, err);}}); }) 此函数将返回…...
)
2023年总结和2024年展望(以ue为主攻)
2023年就要过去了,总结下: 先说好的地方 1,pbr材质集成到了osg中,加上直接光和间接光。终于知道pbr咋回事了。光线追踪的视频也跟着敲了一个。 2,得到了认可。拿到了半年奖,leader让我明年和架构师一起进行…...

南京大学计算机学院面试准备
该内容是我面试南京大学计算机学院保研的时候的准备题目,最后是面试的时候问到的问题。 目录 1. 自我介绍2. 进程和线程的区别3. 循环引用4. 操作系统怎么利用多核?5. 英文介绍二叉搜索树6. 英文介绍二叉搜索树的时间复杂度7. 介绍 stackover flow8. 什…...
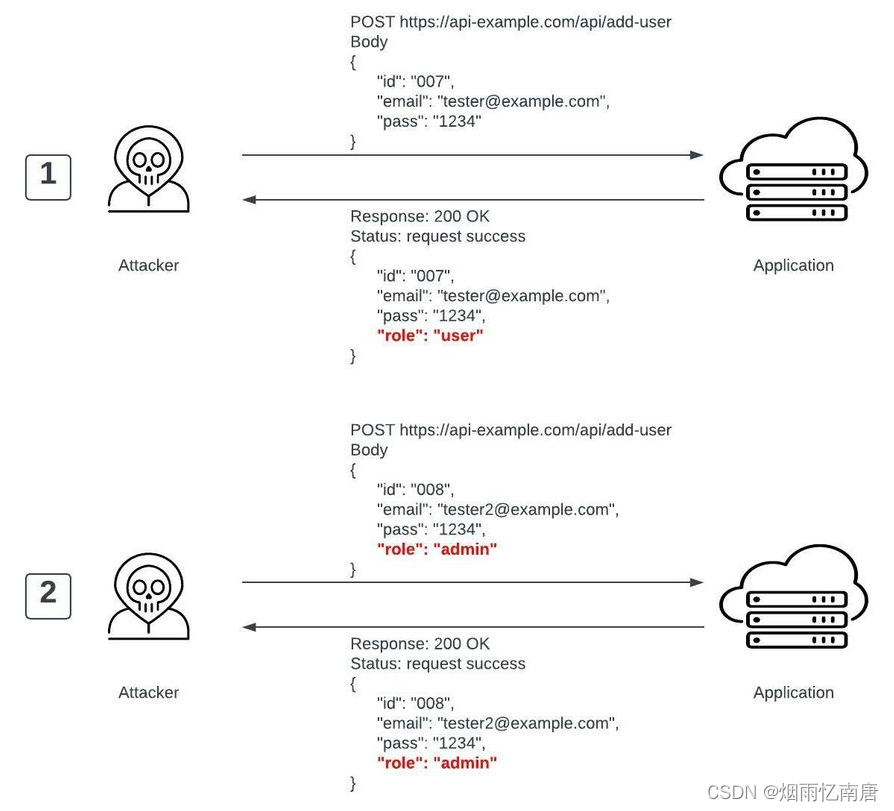
API成批分配漏洞介绍与解决方案
一、API成批分配漏洞介绍 批量分配:在API的业务对象或数据结构中,通常存在多个属性,攻击者通过篡改属性值的方式,达到攻击目的。比如通过设置user.is_admin和user.is_manager的值提升用户权限等级;假设某API的默认接口…...

跨网文件摆渡系统:安全、可控的数字传输桥梁
在企业高度信息化的时代,数据的流通与共享已经成为企业、组织乃至个人之间不可或缺的沟通方式。然而,在数据流通的过程中,我们经常会遇到各种难题和挑战,尤其是当涉及到不同网络环境之间的文件传输。这不仅需要保证文件的安全性&a…...

线程池的原理和基本使用~
线程池的基本原理: 无论是之前在JavaSE基础中,我们学习过的常量池,还是在操作数据库时,我们学习过数据库连接池,以及接下来要学习的线程池,均是一种池化思想,其目的就是为了提高资源的利用率&a…...
PyTorch2.0环境搭建
一、安装python并配置环境变量 1、打开python官网,下载并安装 Welcome to Python.org 下载 寻找版本:推荐使用3.9版本,或其他表中显示为安全(security)的版本 安装:(略) 2、配置环…...

figma 基础使用 —— 常用方法
一、 导入组件 分成两种方式 (1)离线的包导入(iOS 常用组件.fig 直接拖拽到figma最近网页) (2)在插件市场下载https://www.figma.com/community 二、figma中使用标尺 快捷键:shift R 三、插件…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
