当前位置： 首页 > news >正文

ALTERNET STUDIO 9.1 Crack

news 2026/2/8 7:49:46

ALTERNET STUDIO 9.1 发布

宣布 AlterNET Studio 9.1 版本今天上线。AlterNET Studio 9.0 是一个中期更新，重点是改进我们所有的组件库。

以下是 AlterNET Studio 9.1 的发布亮点：

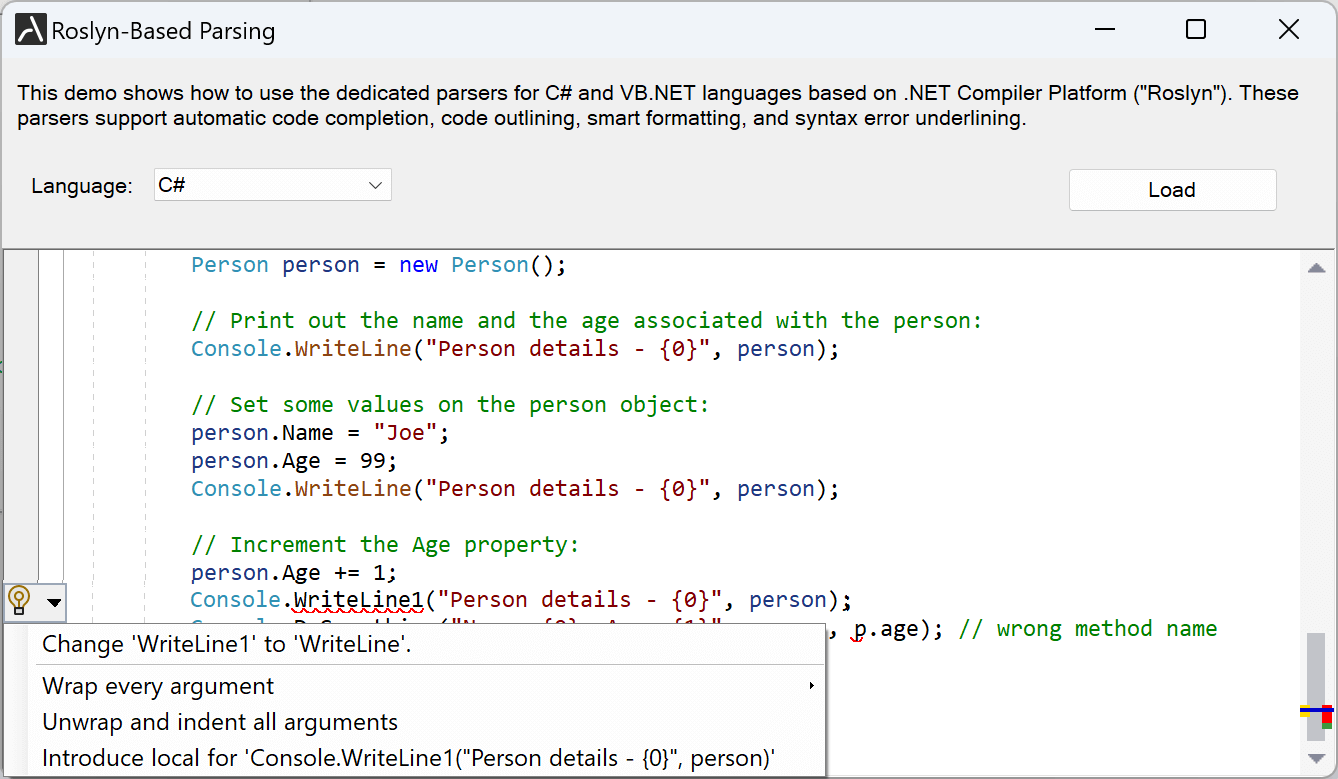
Roslyn C# 和 Visual Basic 解析器现在支持代码修复/代码重构。

代码修复允许用户修复某些类型的错误，例如实现接口、修复拼写错误或在使用列表中添加缺少的名称空间，而代码重构则有助于修改代码以使其更易于维护、理解和扩展，但不改变其行为。当代码修复/代码重构可用于代码中的当前位置时，代码编辑器会显示一个特殊的代码操作图像，用户可以单击该图像并从弹出菜单中选择适当的代码操作。

代码修复和代码重构

Python 和 IronPython 的改进

IronPython 脚本编写器和脚本调试器现在支持 IronPython 3.4。由于 IronPython 3 和 IronPython 2 并非 100% 兼容，因此我们添加了一个可与 IronPython 2 配合使用的NuGet包。

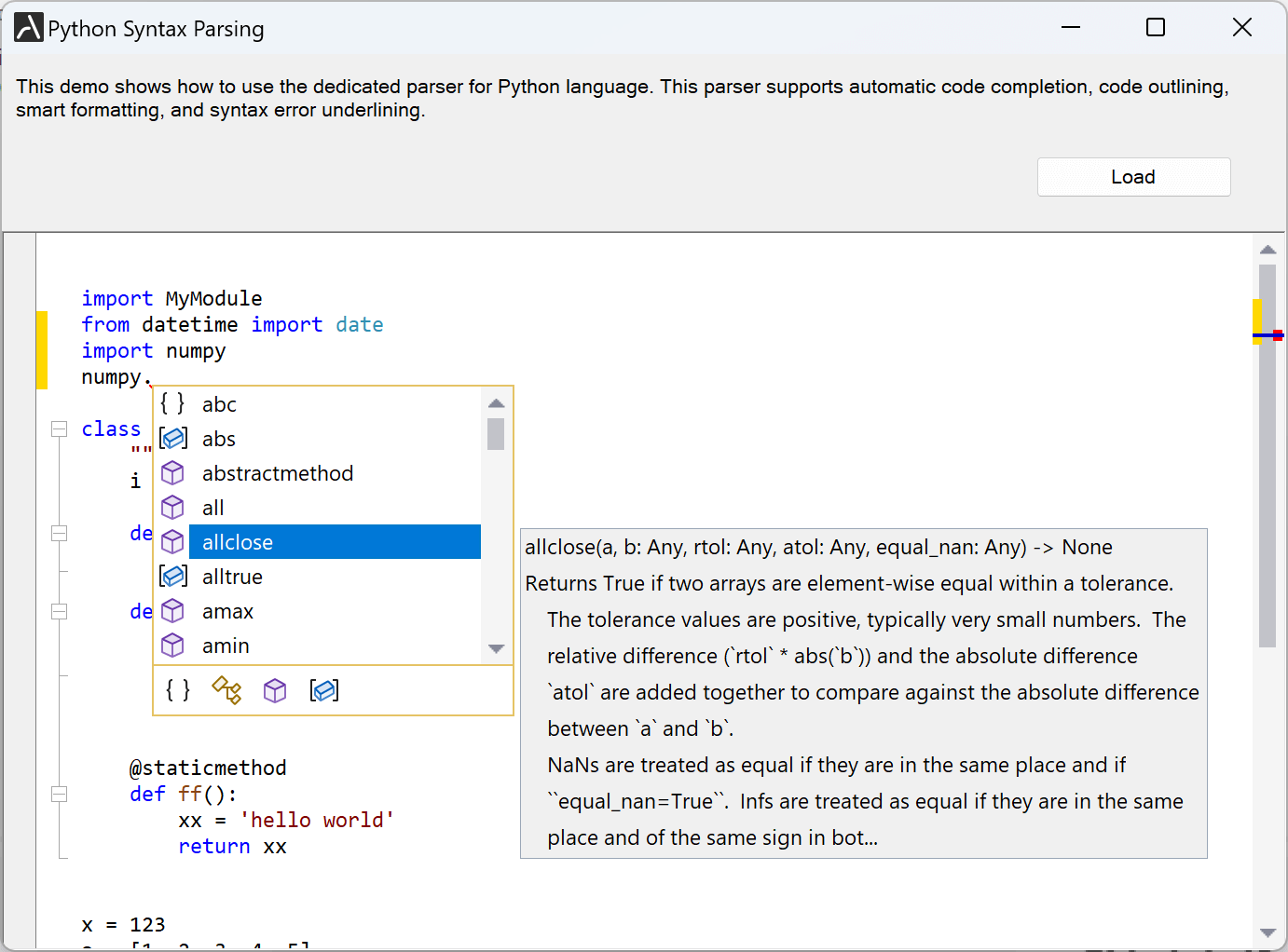
我们还为我们的高级 Python 解析器实现了第三方包的代码补全，例如 NumPy。

用于 NumPy 的 Python IntelliSense

脚本编写器改进

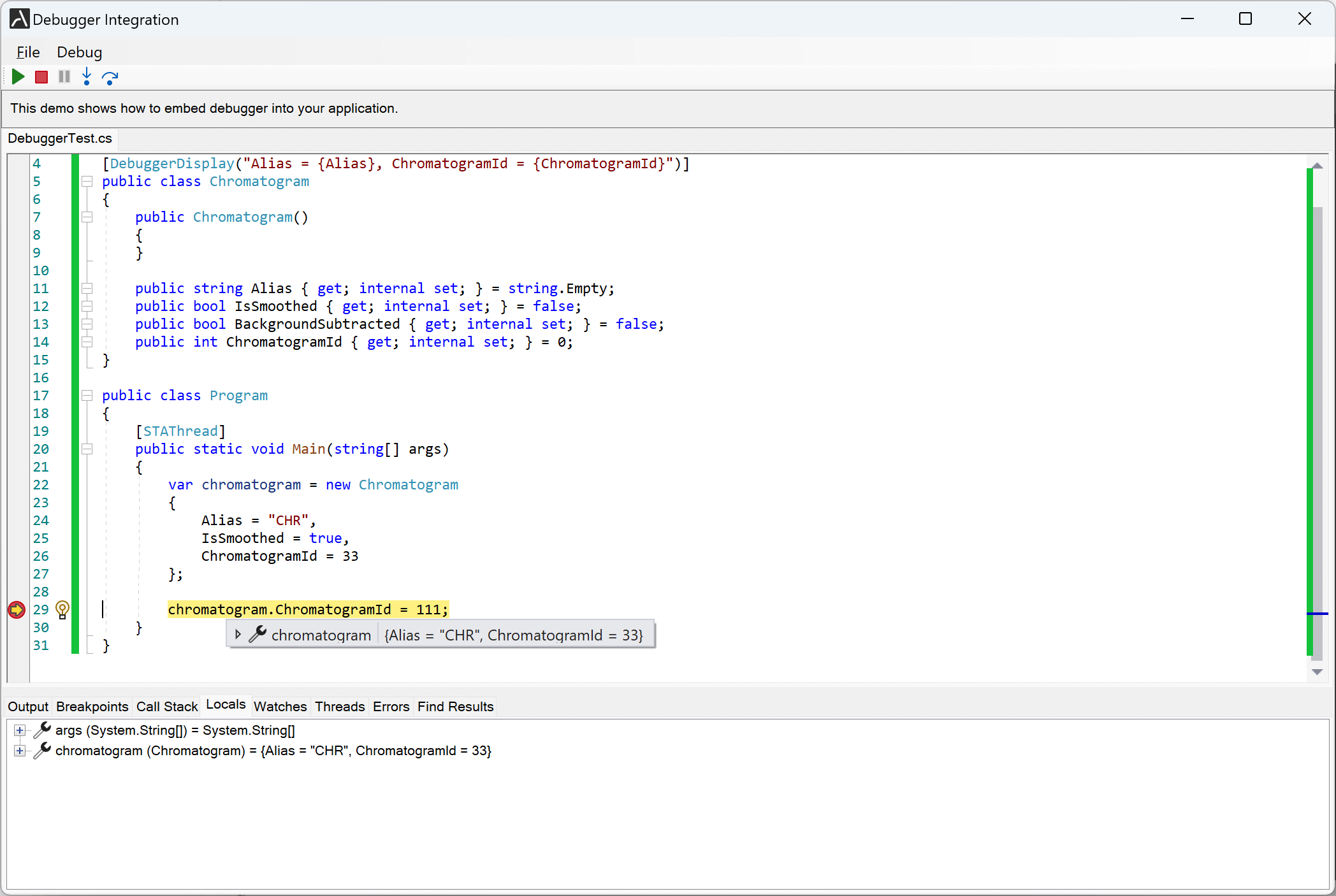
我们现在支持 DebuggerDisplay 属性，该属性为调试器工具提示和监视提供用户定义的信息。

调试器显示属性

表单设计器的改进
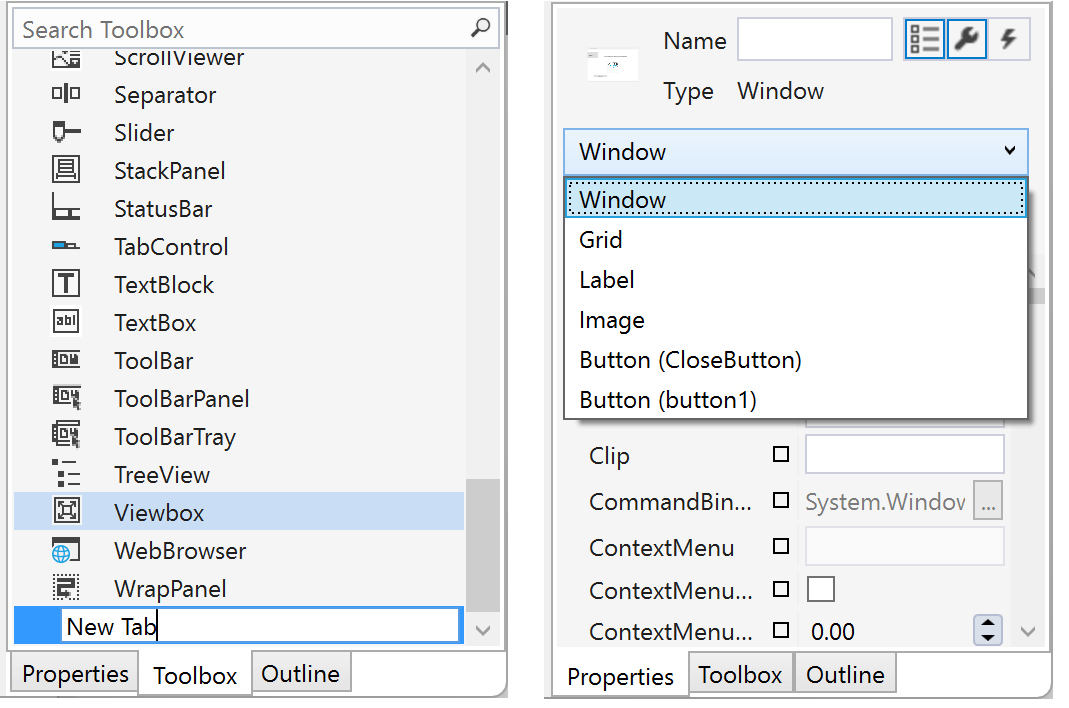
我们添加了一个组件列表，它提供了一种简单的方法来选择表单上的组件以及工具箱项目和类别的就地编辑。

工具箱编辑

阿尔特网工作室
用于代码编辑、脚本编写和用户界面设计的 Windows 窗体和 WPF .NET 组件库。

AlterNET Studio 允许您通过代码编辑、脚本执行和用户界面设计功能来扩展 Windows 窗体或 WPF .NET 应用程序。

代码编辑器
代码编辑器与 Visual Studio 文本编辑器的大部分功能相匹配，最适合 C#、Visual Basic、TypeScript、JavaScript、Python 和 XML 代码编写。

脚本程序
Scripter 允许用户执行 C#、VisualBasic、TypeScript、JavaScript、Python 和 IronPython 脚本，并为脚本调试提供功能齐全的调试引擎。

表单设计师
表单设计器是一个代表设计界面的图形控件，它提供了一种快速便捷的方式来创建图形用户界面。

备用网用户界面
AlterNET UI 是一个跨平台库，用于开发在 Windows、macOS 和 Linux 上运行的轻量级 .NET 桌面应用程序。
  
AlterNET UI 提供了一个 UI 框架和一组标准控件，例如 Text Box、Label、CheckBox、Button、Image、TreeView、ListView 等。AlterNET UI 使用 C# 编写并构建在 .NET Framework 上。它使用类似 XAML 的方法来定义用户界面和布局，允许 .NET 开发人员立即使用他们的技能来创建跨平台或本机 macOS/Linux 应用程序。

 

相关文章：

ALTERNET STUDIO 9.1 Crack

ALTERNET STUDIO 9.1 发布 宣布 AlterNET Studio 9.1 版本今天上线。AlterNET Studio 9.0 是一个中期更新，重点是改进我们所有的组件库。 以下是 AlterNET Studio 9.1 的发布亮点： Roslyn C# 和 Visual Basic 解析器现在支持代码修复/代码重构。 代码修复…...

编程日记 2023/12/8 23:12:02

基于Java技术的选课管理系统设计与实现

末尾获取源码 开发语言：Java Java开发工具：JDK1.8 后端框架：SSM 前端：采用JSP技术开发 数据库：MySQL5.7和Navicat管理工具结合 服务器：Tomcat8.5 开发软件：IDEA / Eclipse 是否Maven项目&#x…...

编程日记 2023/12/8 23:11:01

在UBUNTU上使用Qemu和systemd-nspawn搭建RISC-V轻量级用户模式开发环境

参考链接 使用Qemu和systemd-nspawn搭建RISC-V轻量级用户模式开发环境 - 知乎 安装Qemu sudo apt updatesudo apt -y install qemu-user-binfmt qemu-user-static systemd-container sudo apt -y install zstd 配置环境 RISCV_FILEarchriscv-2023-10-09.tar.zstwget -c ht…...

编程日记 2023/12/8 23:10:00

JAVA使用POI向doc加入图片

JAVA使用POI向doc加入图片 前言 刚来一个需求需要导出一个word文档，文档内是系统某个界面的各种数据图表，以图片的方式插入后导出。一番查阅资料于是乎着手开始编写简化demo,有关参考poi的文档查阅 Apache POI Word(docx) 入门示例教程 网上大多数是XXX…...

编程日记 2023/12/8 23:08:59

反向传播算法

反向传播算法的数学解释 反向传播算法是深度学习中用于训练神经网络的核心算法。它通过计算损失函数相对于网络权重的梯度来更新权重，从而最小化损失。 反向传播的基本原理 反向传播算法基于链式法则，它按层反向传递误差，从输出层开始&…...

编程日记 2023/12/8 23:05:55

记录 | ubuntu降低内核版本的方法

降低 ubuntu 内核，比如降低到 4.15 版本，下载对应 4.15.0.128 内核离线安装，网址： http://archive.ubuntu.com/ubuntu/pool/main/l/linux/， 根据实际选择下载，我这里选择，安装的话采用 dpkg -i …...

编程日记 2023/12/8 23:00:52

MX6ULL学习笔记 (八) platform 设备驱动实验

前言： 什么是 Linux 下的 platform 设备驱动 Linux下的字符设备驱动一般都比较简单，只是对IO进行简单的读写操作。但是I2C、SPI、LCD、USB等外设的驱动就比较复杂了，需要考虑到驱动的可重用性，以避免内核中存在大量重复代码&…...

编程日记 2023/12/8 22:58:51

初识Linux：权限（2）

目录 权限 用户（角色） 文件权限属性 文件的权限属性： 有无权限的区别： 身份匹配： 拥有者、所属组的修改： 八进制的转化： 文件的类型： x可执行权限为什么不能执行&#xf…...

编程日记 2023/12/8 22:57:50

测试环境使用问题及其优化对策实践

1 背景及问题 G.J.Myers在<软件测试技巧>中提出&#xff1a;测试是为了寻找错误而运行程序的过程&#xff0c;一个好的测试用例是指很可能找到迄今为止尚未发现的错误的测试&#xff0c; 一个成功的测试是揭示了迄今为止尚未发现的错误的测试。 对于新手来说&#xff0…...

编程日记 2023/12/8 22:56:49

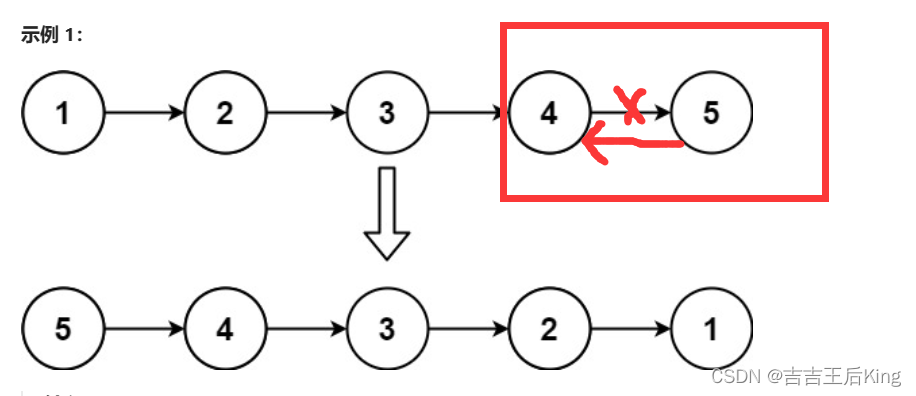
【力扣】206.反转链表

206.反转链表 这道题有两种解法&#xff0c;但不只有两种&#xff0c;嘿嘿。 法一&#xff1a;迭代法 就是按循序遍历将每一个指针的指向都给改了。比如说1——>2——>3改为null<——1<——2<——3这样。那这里以第二个结点为例&#xff0c;想一想。我想要指向…...

编程日记 2023/12/8 22:54:47

Python：核心知识点整理大全7-笔记

目录 4.2.5 遗漏了冒号 4.3 创建数值列表 4.3.1 使用函数 range() 4.3.2 使用 range()创建数字列表 结果如下&#xff1a; 4.3.3 对数字列表执行简单的统计计算 4.3.4 列表解析 4.4 使用列表的一部分 4.4.1 切片 4.4.2 遍历切片 4.4.3 复制列表 4.2.5 遗漏了冒号 fo…...

编程日记 2023/12/8 22:53:46

Hadoop学习笔记（HDP）-Part.15 安装HIVE

目录 Part.01 关于HDP Part.02 核心组件原理 Part.03 资源规划 Part.04 基础环境配置 Part.05 Yum源配置 Part.06 安装OracleJDK Part.07 安装MySQL Part.08 部署Ambari集群 Part.09 安装OpenLDAP Part.10 创建集群 Part.11 安装Kerberos Part.12 安装HDFS Part.13 安装Ranger …...

编程日记 2023/12/8 22:52:45

【力扣100】4.移动零

题目链接 我的题解&#xff1a; class Solution:def moveZeroes(self, nums: List[int]) -> None:"""Do not return anything, modify nums in-place instead."""# 思路是先计算共有几个0&#xff0c;然后remove几次&#xff0c;再末位加几个…...

编程日记 2023/12/8 22:50:43

Filebeat使用指南

Filebeat介绍主要优势主要功能配置日志的解析Kibana中设置日志解析安装步骤安装Filebeat安装监控通过prometheus监控 Filebeat和Logstash的主要区别 Filebeat介绍 Filebeat是使用Golang实现的轻量型日志采集器&#xff0c;也是Elasticsearch stack的一员。它可以作为一个agent…...

编程日记 2023/12/8 22:49:42

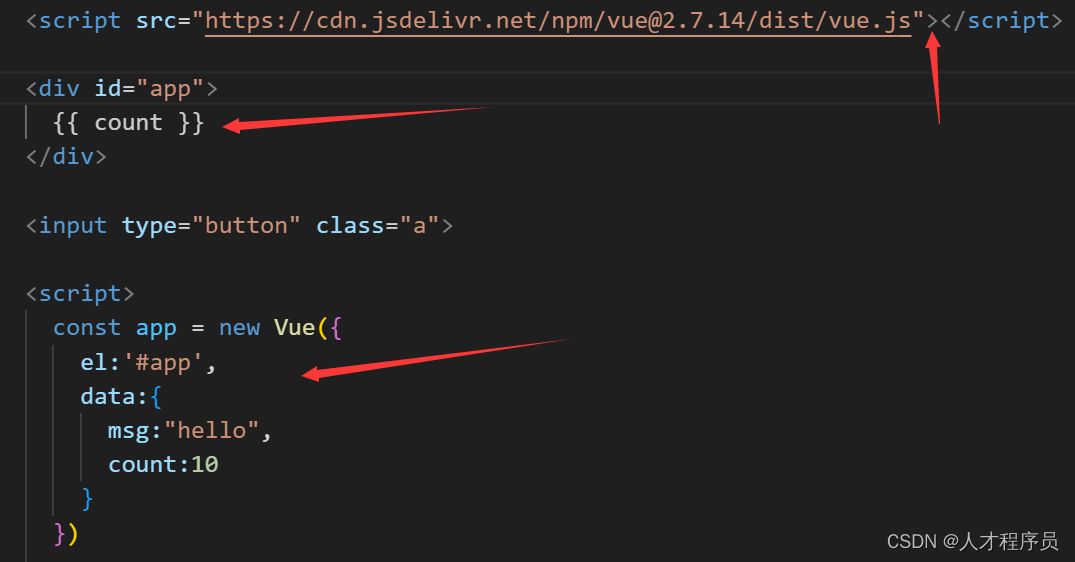
【Vue2】Vue的介绍与Vue的第一个实例

文章目录 前言一、为什么要学习Vue二、什么是Vue1.什么是构建用户界面2.什么是渐进式Vue的两种开发方式&#xff1a; 3.什么是框架 三、创建Vue实例四、插值表达式 {{}}1.作用&#xff1a;利用表达式进行插值&#xff0c;渲染到页面中2.语法3.错误用法 五、响应式特性1.什么是响…...

编程日记 2023/12/8 22:48:41

十五届蓝桥杯分享会（一）

注&#xff1a;省赛4月&#xff0c;决赛6月 一、蓝桥杯整体介绍 1.十四届蓝桥杯软件电子赛参赛人数&#xff1a;C 8w&#xff0c;java/python 2w&#xff0c;web 4k&#xff0c;单片机 1.8w&#xff0c;嵌入式/EDA5k&#xff0c;物联网 300 1.1设计类参赛人数&#xff1a;平…...

编程日记 2023/12/8 22:47:40

原生video设置控制面板controls显示哪些控件

之前我们学习了如何使用原生video播放视频 今天来一个进阶版的——设置控制面板controls显示哪些控件 先看一下当我们使用原生video时&#xff0c;controls属性为true时&#xff0c;相关代码如下&#xff1a; 正常的控制面板默认显示的控件有&#xff1a;播放、时间线、音量调…...

编程日记 2023/12/8 22:46:39

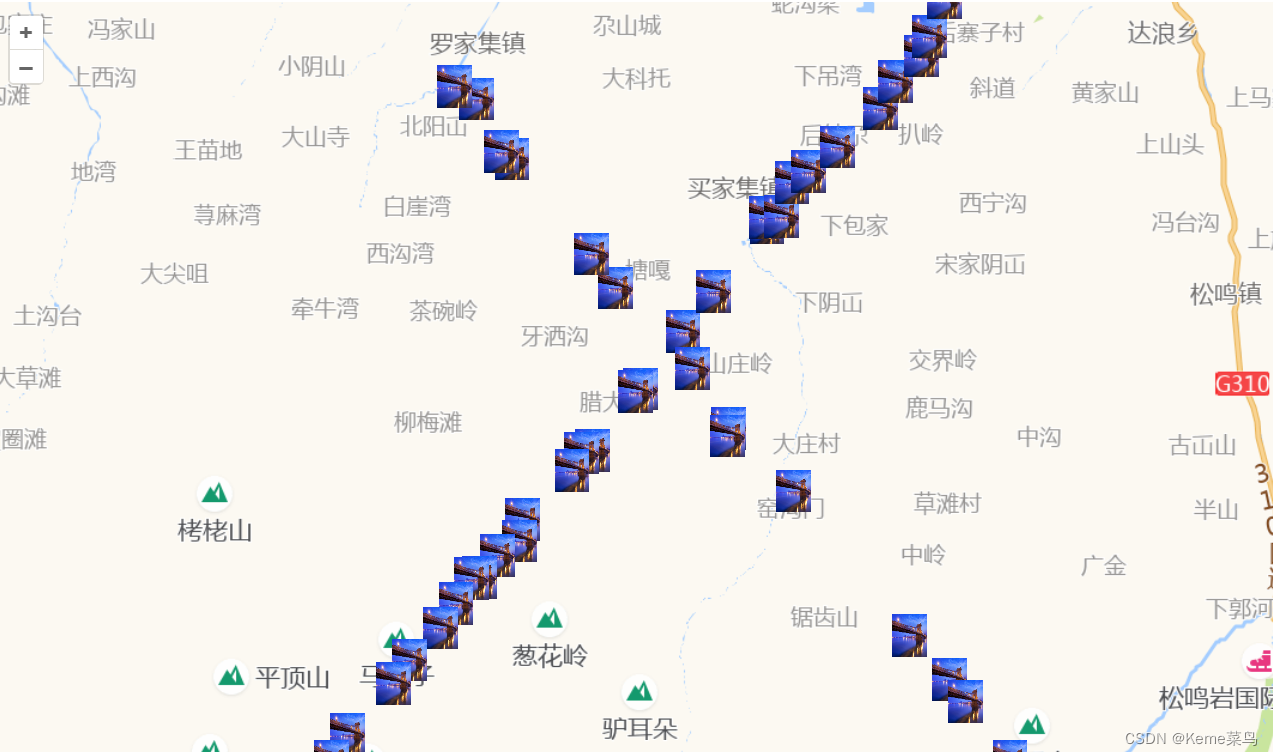
openlayers地图使用---跟随地图比例尺动态标绘大小的一种方式2

openlayers地图使用—跟随地图比例尺动态标绘大小的一种方式2 预期&#xff1a;随着地图比例尺放大缩小&#xff0c;地图上的标绘随着变化尺寸 思路&#xff1a;通过不断添加地图图层实现标绘的动态缩放 优点&#xff1a;标绘放大缩小非常流畅 缺点&#xff1a;标绘超过1000…...

编程日记 2023/12/8 22:44:37

C语言期末考试复习PTA数据类型及表达式-分支结构程序-循环结构-数组经典选择题

目录 第一章&#xff1a;C语言数据类型和表达式 第一题&#xff1a; 第二题&#xff1a; 第三题&#xff1a; 第四题&#xff1a; 第五题&#xff1a; 第六题&#xff1a; 第七题&#xff1a; 第八题&#xff1a; 第九题&#xff1a; 第二章&#xff1a;分支结构程序…...

编程日记 2023/12/8 22:41:36

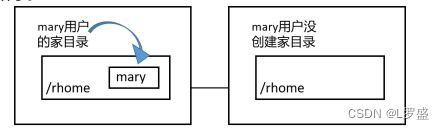
RHEL8_Linux访问NFS存储及自动挂载

本章主要介绍NFS客户端的使用 创建FNS服务器并通过NFS共享一个目录在客户端上访问NFS共享的目录自动挂载的配置和使用 1.访问NFS存储 前面介绍了本地存储&#xff0c;本章就来介绍如何使用网络上的存储设备。NFS即网络文件系统&#xff0c;所实现的是 Linux 和 Linux 之间的共…...

编程日记 2023/12/8 22:34:28

XCTF-web-easyupload

试了试php&#xff0c;php7&#xff0c;pht&#xff0c;phtml等&#xff0c;都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接&#xff0c;得到flag...

编程新知 2026/2/8 3:54:15

装饰模式（Decorator Pattern）重构java邮件发奖系统实战

前言 现在我们有个如下的需求&#xff0c;设计一个邮件发奖的小系统&#xff0c; 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式&#xff08;Decorator Pattern&#xff09;允许向一个现有的对象添加新的功能&#xff0c;同时又不改变其…...

编程新知 2026/2/8 4:37:00

Lombok 的 @Data 注解失效，未生成 getter/setter 方法引发的HTTP 406 错误

HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误&#xff0c;它们的含义、原因和解决方法都有显著区别。以下是详细对比&#xff1a; 1. HTTP 406 (Not Acceptable) 含义&#xff1a; 客户端请求的内容类型与服务器支持的内容类型不匹…...

编程新知 2026/2/1 20:49:03

智慧工地云平台源码，基于微服务架构+Java+Spring Cloud +UniApp +MySql

智慧工地管理云平台系统&#xff0c;智慧工地全套源码&#xff0c;java版智慧工地源码&#xff0c;支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求&#xff0c;提供“平台网络终端”的整体解决方案&#xff0c;提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

编程新知 2026/1/30 15:16:32

Frozen-Flask ：将 Flask 应用“冻结”为静态文件

Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是&#xff1a;将一个 Flask Web 应用生成成纯静态 HTML 文件&#xff0c;从而可以部署到静态网站托管服务上&#xff0c;如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

编程新知 2025/12/5 20:57:13

OkHttp 中实现断点续传 demo

在 OkHttp 中实现断点续传主要通过以下步骤完成&#xff0c;核心是利用 HTTP 协议的 Range 请求头指定下载范围&#xff1a; 实现原理 Range 请求头&#xff1a;向服务器请求文件的特定字节范围&#xff08;如 Range: bytes1024-&#xff09; 本地文件记录&#xff1a;保存已…...

编程新知 2025/12/12 0:56:22

k8s业务程序联调工具-KtConnect

概述 原理 工具作用是建立了一个从本地到集群的单向VPN&#xff0c;根据VPN原理&#xff0c;打通两个内网必然需要借助一个公共中继节点&#xff0c;ktconnect工具巧妙的利用k8s原生的portforward能力&#xff0c;简化了建立连接的过程&#xff0c;apiserver间接起到了中继节…...

编程新知 2026/2/1 4:14:14

学校时钟系统，标准考场时钟系统，AI亮相2025高考，赛思时钟系统为教育公平筑起“精准防线”

2025年#高考 将在近日拉开帷幕&#xff0c;#AI 监考一度冲上热搜。当AI深度融入高考&#xff0c;#时间同步 不再是辅助功能&#xff0c;而是决定AI监考系统成败的“生命线”。 AI亮相2025高考&#xff0c;40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕&#xff0c;江西、…...

编程新知 2026/2/3 2:10:25

Xen Server服务器释放磁盘空间

disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

编程新知 2025/11/19 6:04:18

处理vxe-table 表尾数据是单独一个接口，表格tableData数据更新后，需要点击两下，表尾才是正确的

修改bug思路&#xff1a; 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑&#xff1a;async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

编程新知 2026/1/25 6:16:49