有限差分法-差商公式及其Matlab实现
2.1 有限差分法
有限差分法 (finite difference method)是一种数值求解偏微分方程的方法,它将偏微分方程中的连续变量离散化为有限个点上的函数值,然后利用差分逼近导数,从而得到一个差分方程组。通过求解差分方程组,可以得到原偏微分方程的数值解。
有限差分法是一种历史悠久且十分成熟的数值方法,其基本思想可以追溯到18世纪。在20世纪上半叶,随着电子计算机的发展,有限差分法逐渐成为求解偏微分方程的重要方法之一。目前,有限差分法已广泛应用于各种科学工程领域,如物理、工程、地球科学、生物医学、金融等。
有限差分法的应用非常广泛,可以用于求解各种偏微分方程,如抛物型、双曲型和椭圆型偏微分方程。它的优点是简单易懂,容易实现,且精度可控。缺点是需要将连续变量离散化,因此离散化的精度会影响最终的数值解的精度。
在实际应用中,有限差分法通常与其他数值方法结合使用,如有限元法、边界元法、谱方法等。这些方法各有特点,可以针对不同的问题选择合适的方法求解。相关书籍众多。本专栏只介绍其简单的应用, 来帮助读者了解数值方法的发展过程。
2.1.1 有限差分法中的数值微分
数值微分是根据函数在一些离散点的值计算它在某点的 1 阶导数或高阶导数近似值的 方法。先从一个最简单的例子开始, 在区间 [ a , b ]
相关文章:

有限差分法-差商公式及其Matlab实现
2.1 有限差分法 有限差分法 (finite difference method)是一种数值求解偏微分方程的方法,它将偏微分方程中的连续变量离散化为有限个点上的函数值,然后利用差分逼近导数,从而得到一个差分方程组。通过求解差分方程组,可以得到原偏微分方程的数值解。 有限差分法是一种历史…...

高校就业信息管理系统
1引言 1.1编写目的 1.2背景 1.3定义 1.4参考资料 2程序系统的结构 3登录模块设计说明一 3.1程序描述 3.2功能 3.3性能 3.4输人项 3.5输出项 3.6算法 3.7流程逻辑 3.8接口 3.10注释设计 3.11限制条件 3.12测试计划 3.13尚未解决的问题 4注册模块设计说明 4.…...

【Java|golang】2373. 矩阵中的局部最大值
给你一个大小为 n x n 的整数矩阵 grid 。 生成一个大小为 (n - 2) x (n - 2) 的整数矩阵 maxLocal ,并满足: maxLocal[i][j] 等于 grid 中以 i 1 行和 j 1 列为中心的 3 x 3 矩阵中的 最大值 。 换句话说,我们希望找出 grid 中每个 3 x …...
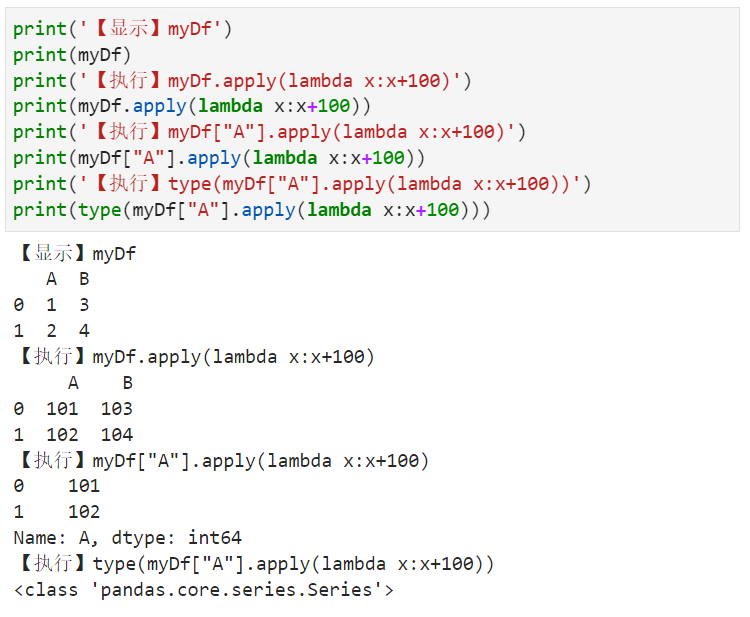
根据指定函数对DataFrame中各元素进行计算
【小白从小学Python、C、Java】【计算机等级考试500强双证书】【Python-数据分析】根据指定函数对DataFrame中各元素进行计算以下错误的一项是?import numpy as npimport pandas as pdmyDict{A:[1,2],B:[3,4]}myDfpd.DataFrame(myDict)print(【显示】myDf)print(myDf)print(【…...

【蓝桥杯集训·每日一题】AcWing 3502. 不同路径数
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴一、题目 1、原题链接 3502. 不同路径数 2、题目描述 给定一个 nm 的二维矩阵,其中的每个元素都是一个 [1,9] 之间的正整数。 从矩阵中的任意位置出发…...
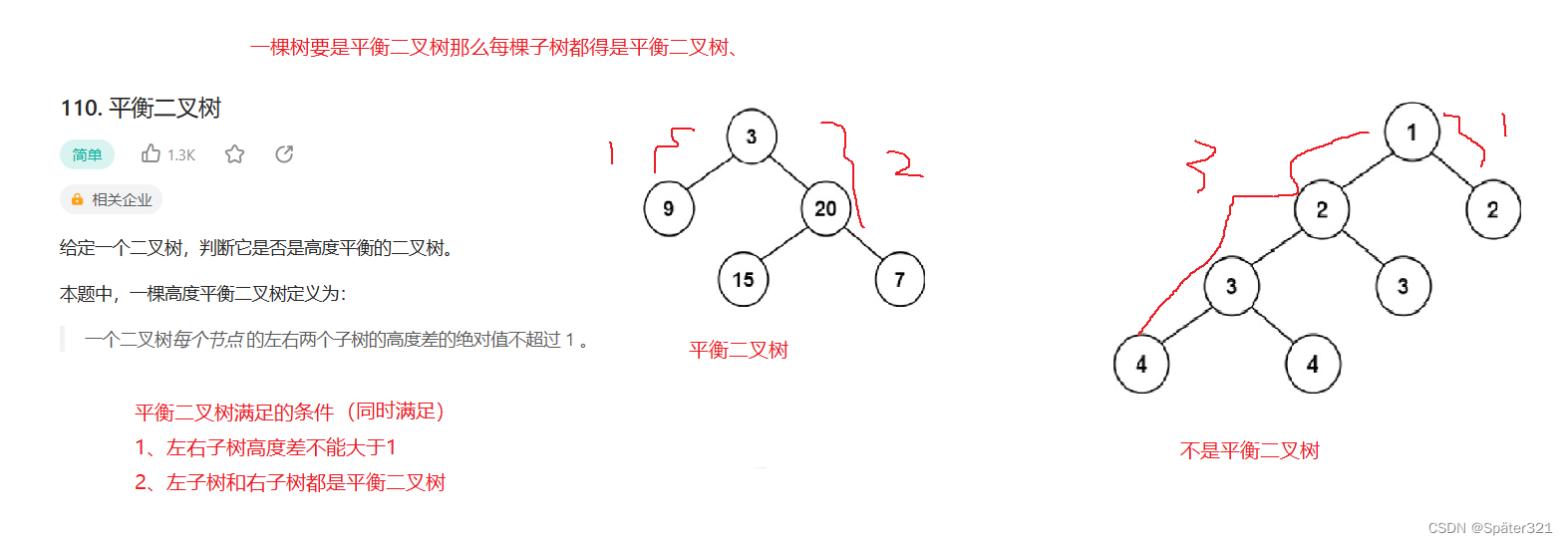
Java - 数据结构,二叉树
一、什么是树 概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点: 1、有…...
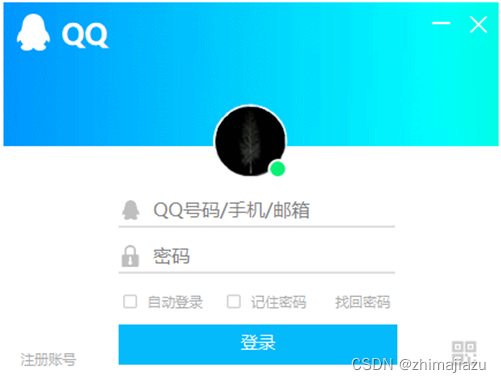
模拟QQ登录-课后程序(JAVA基础案例教程-黑马程序员编著-第十一章-课后作业)
【案例11-3】 模拟QQ登录 【案例介绍】 1.案例描述 QQ是现实生活中常用的聊天工具,QQ登录界面看似小巧、简单,但其中涉及的内容却很多,对于初学者练习Java Swing工具的使用非常合适。本案例要求使用所学的Java Swing知识,模拟实…...
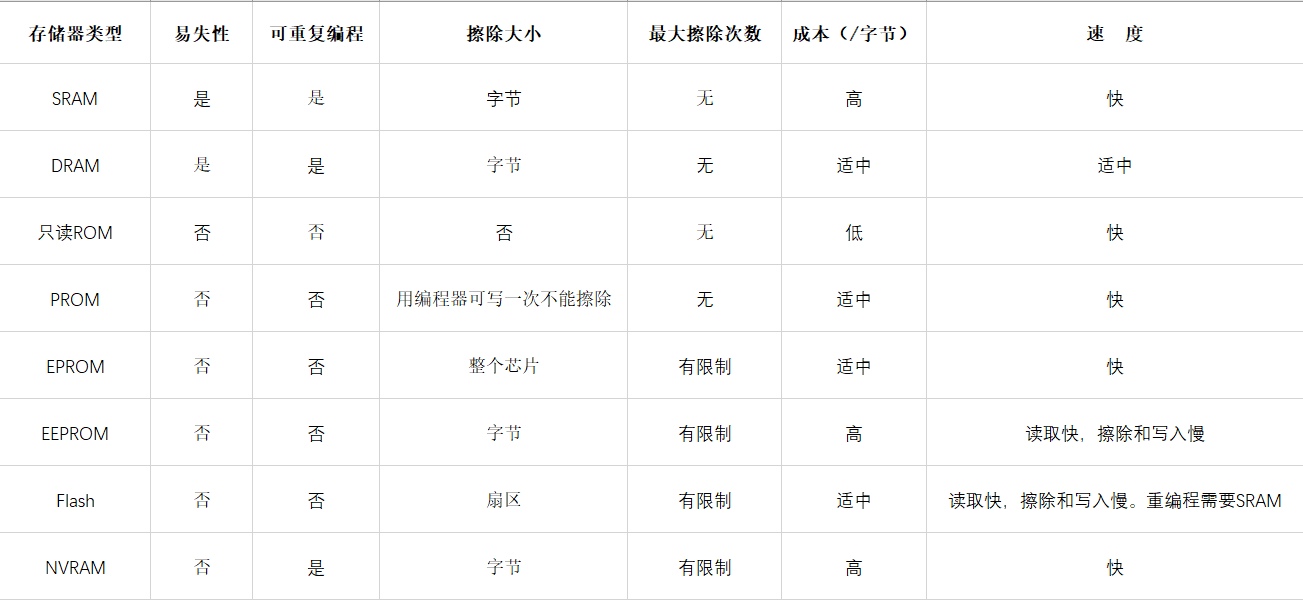
【壹】嵌入式系统硬件基础
随手拍拍💁♂️📷 日期: 2023.2.28 地点: 杭州 介绍: 日子像旋转毒马🐎,在脑海里转不停🤯 🌲🌲🌲🌲🌲 往期回顾 🌲🌲🌲…...
当参数调优无法解决kafka消息积压时可以这么做
今天的议题是:如何快速处理kafka的消息积压 通常的做法有以下几种: 增加消费者数增加 topic 的分区数,从而进一步增加消费者数调整消费者参数,如max.poll.records增加硬件资源 常规手段不是本文的讨论重点或者当上面的手段已经使…...
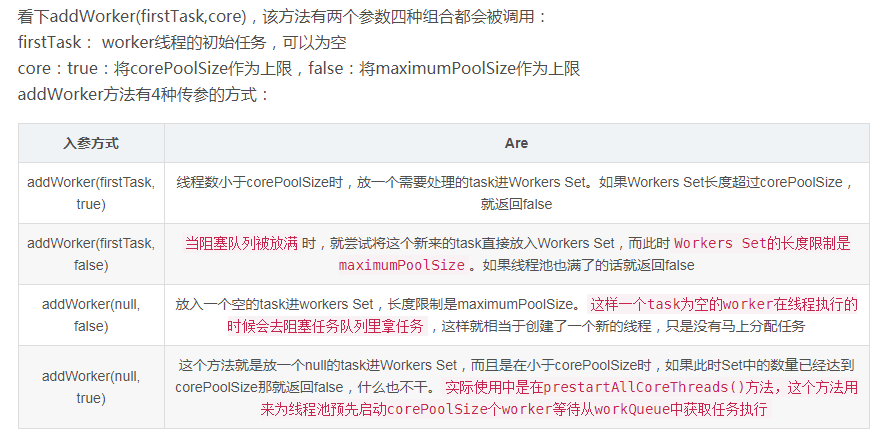
Java线程池源码分析
Java 线程池的使用,是面试必问的。下面我们来从使用到源码整理一下。 1、构造线程池 通过Executors来构造线程池 1、构造一个固定线程数目的线程池,配置的corePoolSize与maximumPoolSize大小相同, 同时使用了一个无界LinkedBlockingQueue存…...
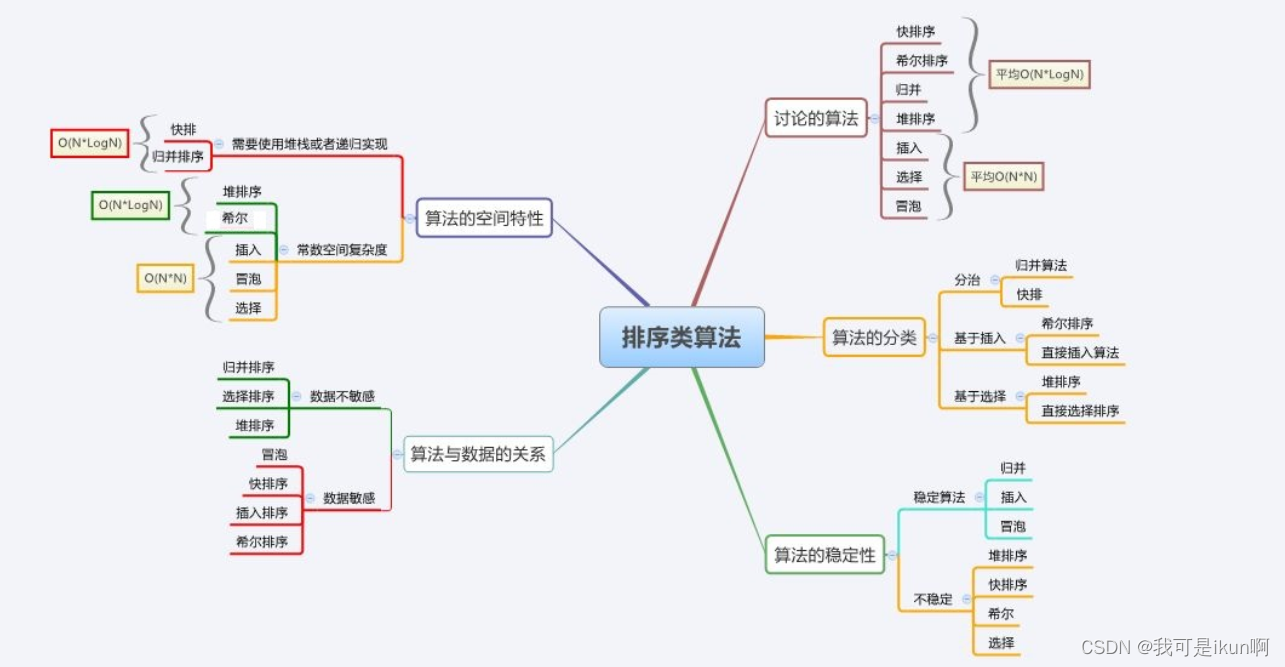
手撕八大排序(下)
目录 交换排序 冒泡排序: 快速排序 Hoare法 挖坑法 前后指针法【了解即可】 优化 再次优化(插入排序) 迭代法 其他排序 归并排序 计数排序 排序总结 结束了上半章四个较为简单的排序,接下来的难度将会大幅度上升&…...
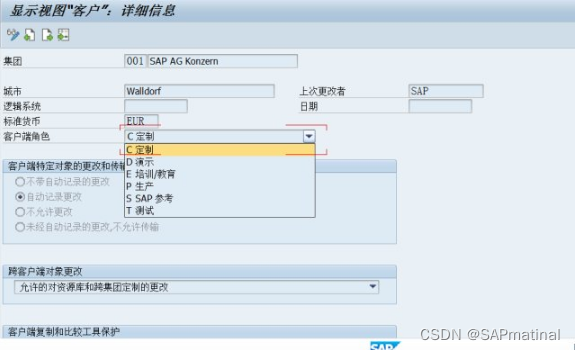
SAP 详细解析SCC4
事务代码:SCC4,选择一个客户端,点击进入,如图: 一、客户端角色 客户控制:客户的角色(生产性,测试,...) 此属性表示 R/3 系统中的客户端角色。其中可能包括…...
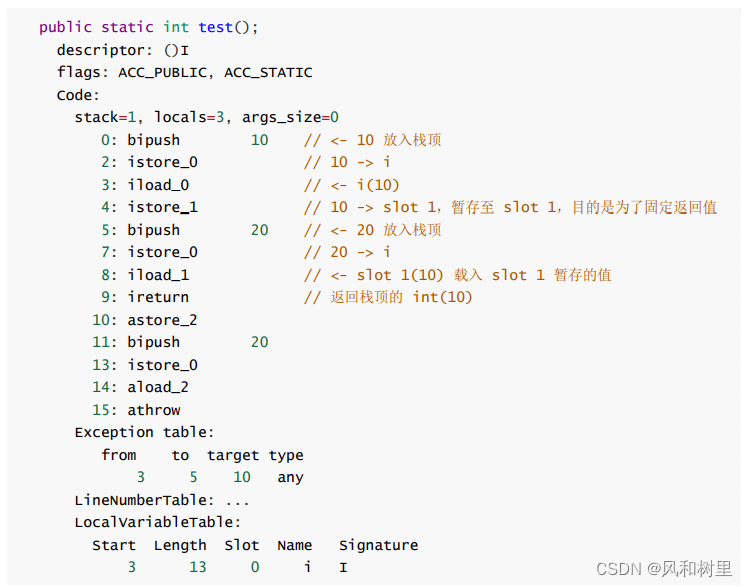
java异常分类和finally代码块中return语句的影响
首先看一下java中异常相关类的继承关系: 引用 1、分类 异常可以分为受查异常和非受查异常,Error和RuntimeException及其所有的子类都是非受查异常,其他的是受查异常。 两者的区别主要在: 受检的异常是由编译器(编译…...

【链表OJ题(二)】链表的中间节点
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:数据结构 🎯长路漫漫浩浩,万事皆有期待 文章目录链表OJ题(二)1. 链表…...
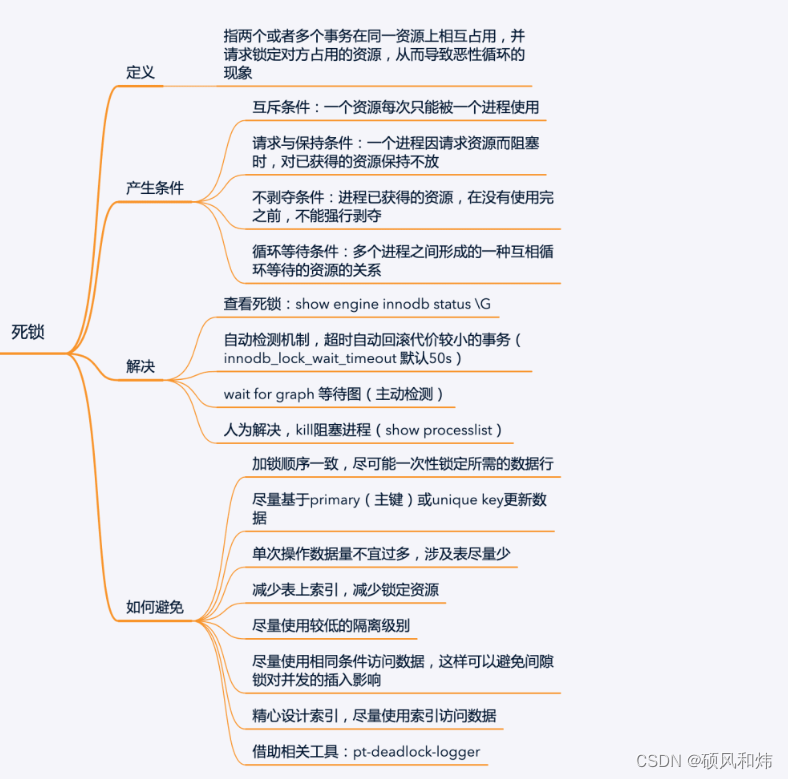
【强烈建议收藏:MySQL面试必问系列之并发事务锁专题】
一.知识回顾 上节课我们一起学习了MySQL面试必问系列之事务,没有学习的同学可以看一下上一篇文章,肯定对你会有帮助,学习过的同学肯定知道,上节课我们留了一个小尾巴,这个小尾巴是什么呢?就是没有详细展开…...
Linux下使用Makefile实现条件编译
在Linux系统下Makefile和C/C语言都有提供条件选择编译的语法,就是在编译源码的时候,可以选择性地编译指定的代码。这种条件选择编译的使用场合有好多,例如我们开发一个兼容标准版本与定制版本兼容的项目,那么,一些与需…...
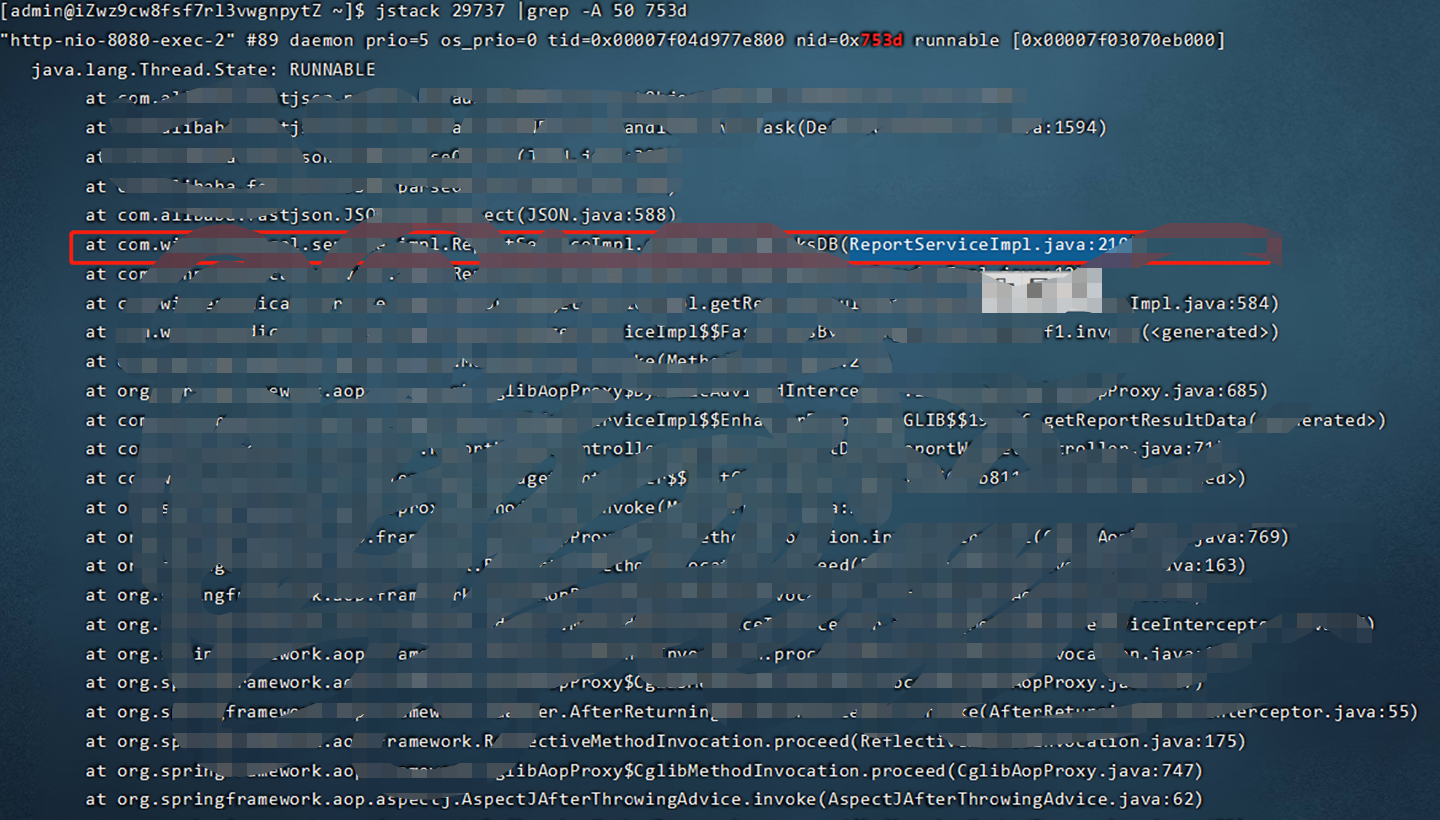
java 应用cpu飙升(超过100%)故障排查
前言害。。。昨天刚写完一份关于jvm问题排查相关的博客,今天线上项目就遇到了一个突发问题。现象是用户反映系统非常卡,无法操作。然后登录服务器查看发现cpu 一直100%以上。具体排查步骤:1,首先top命令查看服务器cpu等情况&#…...
光学设计软件Ansys的Lumerical 2023版本下载与安装使用
文章目录前言一、许可管理工具安装二、许可管理器配置三、Lumerical安装四、工具使用配置总结前言 Lumerical是一款功能强大的软件,用于设计和分析从组件到系统阶段的光子学和电磁学。这个版本的Lumerical改进了电子和光子学设计工具,用于复杂光子学&am…...
Java 异常
文章目录1. 异常概述2. JVM 的默认处理方案3. 异常处理之 try...catch4. Throwable 的成员方法5. 编译异常和运行异常的区别6. 异常处理之 throws7. 自定义异常8. throws 和 throw 的区别1. 异常概述 异常就是程序出现了不正常的情况。 ① Error:严重问题ÿ…...
JavaSE学习笔记day17
零、 复习昨日 File: 通过路径代表一个文件或目录 方法: 创建型,查找类,判断类,其他 IO 输入& 输出字节&字符 try-catch代码 一、作业 给定路径删除该文件夹 public static void main(String[] args) {deleteDir(new File("E:\\A"));}// 删除文件夹public s…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...

深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀”
深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀” 在JavaScript中,我们经常需要处理文本、数组、对象等数据类型。但当我们需要处理文件上传、图像处理、网络通信等场景时,单纯依赖字符串或数组就显得力不从心了。这时ÿ…...

【R语言编程——数据调用】
这里写自定义目录标题 可用库及数据集外部数据导入方法查看数据集信息 在R语言中,有多个库支持调用内置数据集或外部数据,包括studentdata等教学或示例数据集。以下是常见的库和方法: 可用库及数据集 openintro库 该库包含多个教学数据集&a…...

大模型智能体核心技术:CoT与ReAct深度解析
**导读:**在当今AI技术快速发展的背景下,大模型的推理能力和可解释性成为业界关注的焦点。本文深入解析了两项核心技术:CoT(思维链)和ReAct(推理与行动),这两种方法正在重新定义大模…...
