数据结构之插入排序
目录
前言
插入排序
直接插入排序
插入排序的时间复杂度
希尔排序
前言
在日常生活中,我们不经意间会遇到很多排序的场景,比如在某宝,某东上买东西,我们可以自己自定义价格是由高到低还是由低到高,再比如在王者某耀中的每个英雄的荣耀战力,都是由高到低进行排序的,这些场景都用到了排序,但是这些场景的底层都是用一个个排序算法来实现的,本期开始,我们就要学习数据结构中很重要的一个知识点-------排序。
几种常见的排序:
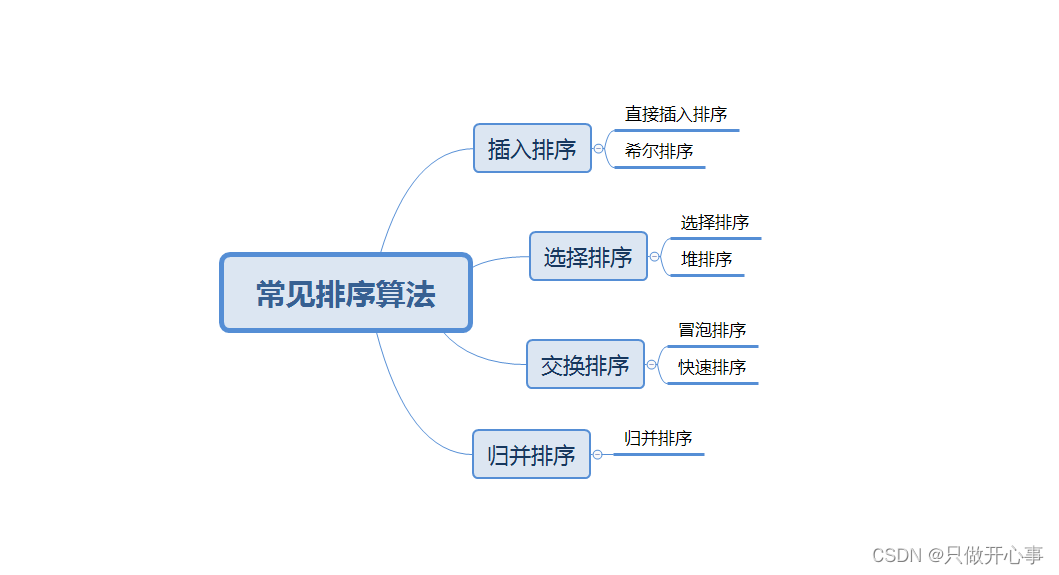
注:我们今后所有的排序都默认排升序。
本期我们主要讲解插入排序。
插入排序
直接插入排序
直接插入排序在现实生活中最常见的应用其实就是斗地主时,我们一般会将牌拍好序,然后根据自己的打法打牌,大家先仔细想想,再给牌整理时我们是怎样整理的呢?当我们摸到第一张牌时,此时它已经有序,我们摸第二张牌时,就会与第一张牌做比较,然后发生交换使之成为我们想要的顺序,当我们摸第三张牌时,我们又会与最后一张牌与倒数第二张牌进行比较,交换之后使牌的顺序成为我们想要的顺序,之后每摸一张牌,就按照此方法进行整理,最后就会得到一个有序的牌列。这就直接插入排序的一个比较常见的应用场景。在数据结构中,我们怎样实现直接插入排序呢?
要实现直接插入排序,我们可以先将直接插入排序分解为单趟排序,然后再让每趟排序组合成为整个排序。
单趟排序:
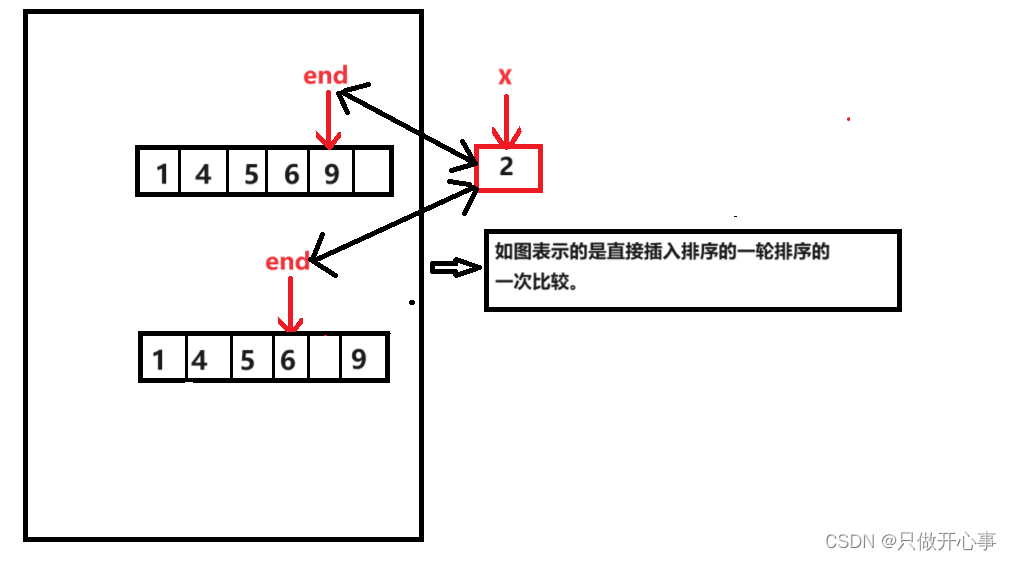
单趟排序的情景:我们要将一个元素插入一个有序数组之中。可以类比,我们摸了一张牌还没有插入手中的牌中,但是手中的牌肯定已经是一个有序的牌序列了。
单趟排序的算法思想:我们令有序的数组的最后一个元素的位置为end,要插入的元素为x。要将x插入一个有序数组,就得先让x与end位置上的元素进行比较,因为我们是排升序,所以如果x比a[end]小,就要把a[end]向后挪动一个位置,然后将end--,然后在让x与此时end位置上的元素a[end]进行比较,比较的原理同上,直到将x插入到合理的位置,那么怎样判断这样的一趟排序已经结束了呢?其实就是x比当前end位置上的元素要大,这是一个结束条件,还有就是x比有序数组所有的元素都要小,即就是要将x放在数组的第一个元素的位置上,此时end已经到了数组第一个元素位置的前一个位置之前,我们称此时end==-1,所以综上,一趟排序的结束标志就是x>a[end]或者end<0
单趟排序代码实现:
int end = size - 1;int x;while (end >= 0){if (a[end] > x){a[end + 1] = a[end];end--;}else {break;}}a[end + 1] = x;到了这里,我们单趟排序已经搞定了,但是上面我们已经说了,我们把整个插入排序分为了每趟排序,那么怎样将每趟排序合并成为直接插入排序呢?
每趟排序的关键点在于是把一个元素插入一个有序数组之中,其实对于一个数组而言,无论它是否是有序还是无序的,其第一个元素毋庸置疑肯定是有序的,这便是关键,我们可以从第一个与元素开始,把第一个元素当成一个有序数组,此时第二个元素就是要插入有序数组中的元素,那么此时第二哥元素插入由第一个元素组成的有序数组中就可以看成是一趟排序,这趟排序之后,第一个元素和第二个元素就组成了一个有序数组,第三个元素插入由第一个和第二个元素组成的有序数组就可以看成第二趟排序,由此依次进行多趟排序,那么整个数组的多趟排序就最终组成了直接插入排序。
直接插入排序完整代码:
void InsertSort(int* a, int size)
{assert(a);for(int end=0;end<size-1;end++){ int x = a[end + 1];while (end >= 0){if (a[end] > x){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = x;}
}
int main()
{int arr[] = { 10,9,8,7,6,5,4,3,2,1 };InsertSort(arr, sizeof(arr) / sizeof(int));for (int i = 0; i < sizeof(arr) / sizeof(int); i++){printf("%d ", arr[i]);}return 0;}运行截图如下:
注意:
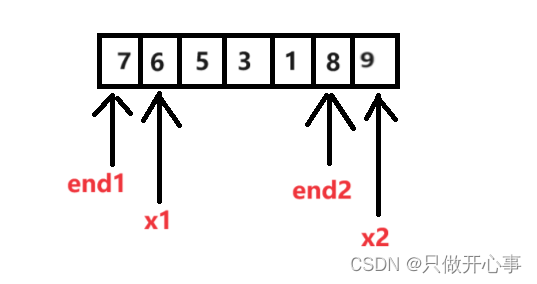
排序这里比较重要的就是边界的控制,对于直接插入排序而言,若数组的大小为size。end的初始值就是0,end的最终值就是size-2,x的初始位置就是1,x的最终位置就是size-1。
以上便是直接插入排序的整个过程。
插入排序的时间复杂度
最好:O(N),已经有序的数组,要插入的元素比end位置上的元素大,只用跟end位置上的元素比较一下。
最坏:O(N^2),逆序,要插入的元素比有序数组的所有元素都要小,跟end位置和end位置之前的所有元素都要比较一下。
稳定性:稳定。
希尔排序
希尔排序其实就是插入排序的进阶版,我们知道,一个数组越有序,直接插入排序的时间复杂度越低,希尔排序其实就是为了将一个无序的数组变得有序,使插入排序变得更加简单。
希尔排序如图:
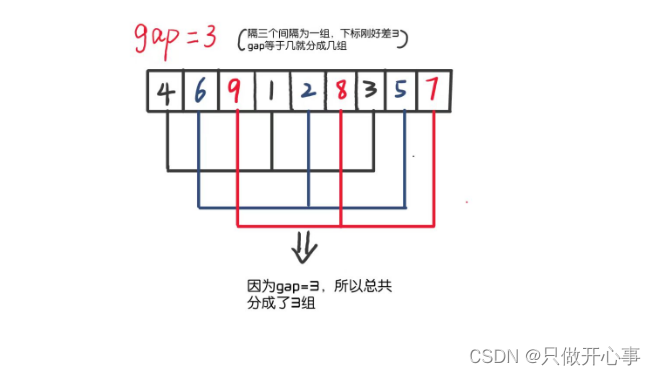
希尔排序的思想:先设置一个gap值,先把整个数组的元素分成gap组,即下标差gap的为一组,然后对每一组按照直接插入排序的思想进行排序,每一组的排序将完成一次预排序,每完成一次预排序,数组会变得比之前更加有序。我们再改变gap的值多次进行预排序,当gap==1时,就是直接插入排序,此时因为经历了多次预排序,整个数组已经变得有序,所以此时再用直接插入排序对整个数组完成最终的排序。
希尔排序的整体代码:
void ShellSort(int* a, int size)
{int gap = size;while (gap > 1){gap /= 2;//进行一趟预排序for (int i = 0; i < gap; i++){//进行每组排序for (int end = i; end < size - gap; end += gap){int x = a[end + gap];//进行单趟排序while (end >= 0){if (a[end] > x){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = x;}}}
}
int main()
{int arr[] = { 10,9,2,8,6,5,4,3,11,1 };ShellSort(arr, sizeof(arr) / sizeof(int));for (int i = 0; i < sizeof(arr) / sizeof(int); i++){printf("%d ", arr[i]);}return 0;
}运行截图如下:

当然,上述的方法是把三组的排序是分开的,每组自己排自己的,但是下面这种方法就是三种排序我们再一次排序中就全部排序完成,更为简洁,但是没有第一种好理解,可以理解为是第一种方法的进阶版本,但是这种进阶版本是我们经常使用的。
进阶版本代码如下:
void ShellSort(int* a, int size)
{int gap = size;while (gap > 1){gap /= 2;//进行一趟预排序,将多组排序在一次排序中就完成了,而不是按组进行排序for (int end = 0; end < size - gap; end++){int x = a[end + gap];//进行单趟排序while (end >= 0){if (a[end] > x){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = x;}}
}
int main()
{int arr[] = { 10,19,2,8,6,0,4,3,11,1 };ShellSort(arr, sizeof(arr) / sizeof(int));for (int i = 0; i < sizeof(arr) / sizeof(int); i++){printf("%d ", arr[i]);}return 0;
}以上便是希尔排序的整个过程。
希尔排序的时间复杂度
希尔排序的时间复杂度为:
1.最好:O(N),当整个数组为有序数组时,复杂度最小。排序算法的时间复杂度的天花板就是O(N)
2.最坏:总共分成了gap组,每组大概就是size/gap个元素,如果每组都逆序,那么每组的复杂度又是一个1+2+...+size/gap的等差数列,平均是O(N^1.3)。
稳定性:不稳定。
插入排序的内容就是这些,我们需要注意的仍然是算法中边界的控制,在编写代码时,我们可以自己画图去控制边界,这是一个很好的方法。
好了,本期的内容到此结束^_^
相关文章:

数据结构之插入排序
目录 前言 插入排序 直接插入排序 插入排序的时间复杂度 希尔排序 前言 在日常生活中,我们不经意间会遇到很多排序的场景,比如在某宝,某东上买东西,我们可以自己自定义价格是由高到低还是由低到高,再比如在王者某…...

2023年江西省“振兴杯”网络信息行业(信息安全测试员)职业技能竞赛 Write UP
文章目录 一、2023csy-web1二、2023csy-web2三、2023csy-web3四、2023csy-web4五、2023csy-misc1六、2023csy-misc2七、2023csy-crypto1八、2023csy-re1 一、2023csy-web1 该题提供一个web靶场,《伟大的挑战者》,分值:5分 web页面一直在播放c…...

【5G PHY】5G NR 如何计算资源块的数量?
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...

解决oracle.sql.TIMESTAMP序列化转换失败问题 及 J2EE13Compliant原理
目录 报错现象报错内容处理方法Oracle驱动源码总结 报错现象 oracle表中存在TIMESTAMP类型的列时,jdbc查出来做序列化时报错 报错内容 org.springframework.web.util.NestedServletException: Request processing failed; nested exception is org.springframewo…...
QQ2023备份
需要修改的路径(共3处) 这三处路径中,只有一处是需要修改的 QQPC端-主菜单-设置-基本设置-文件管理 点击上面的“”自定义“”,然后修改路径即可 修改路径后提示 然后等一会才会关干净QQ的相关进程,关闭后才会有自动…...
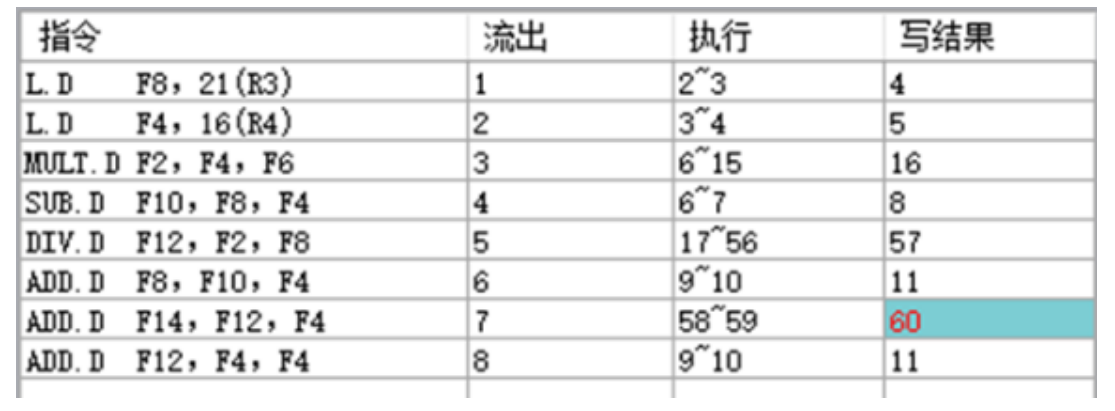
HNU计算机结构体系-实验2:CPU动态指令调度Tomasulo
文章目录 实验2 CPU动态指令调度Tomasulo一、实验目的二、实验说明三、实验内容问题1:问题2:问题3:问题4:问题5: 四、思考题问题1:问题2: 五、实验总结 实验2 CPU动态指令调度Tomasulo 一、实验…...

智慧城市是什么?为什么要建智慧城市?
智慧城市是一个通过现代科技手段推动城市管理和服务创新的概念。 具体来说,它利用信息技术和创新概念,将城市的各个系统和服务集成起来,以提升城市运行效率、优化城市管理和服务,改善市民的生活质量。 为什么要建智慧城市呢&…...
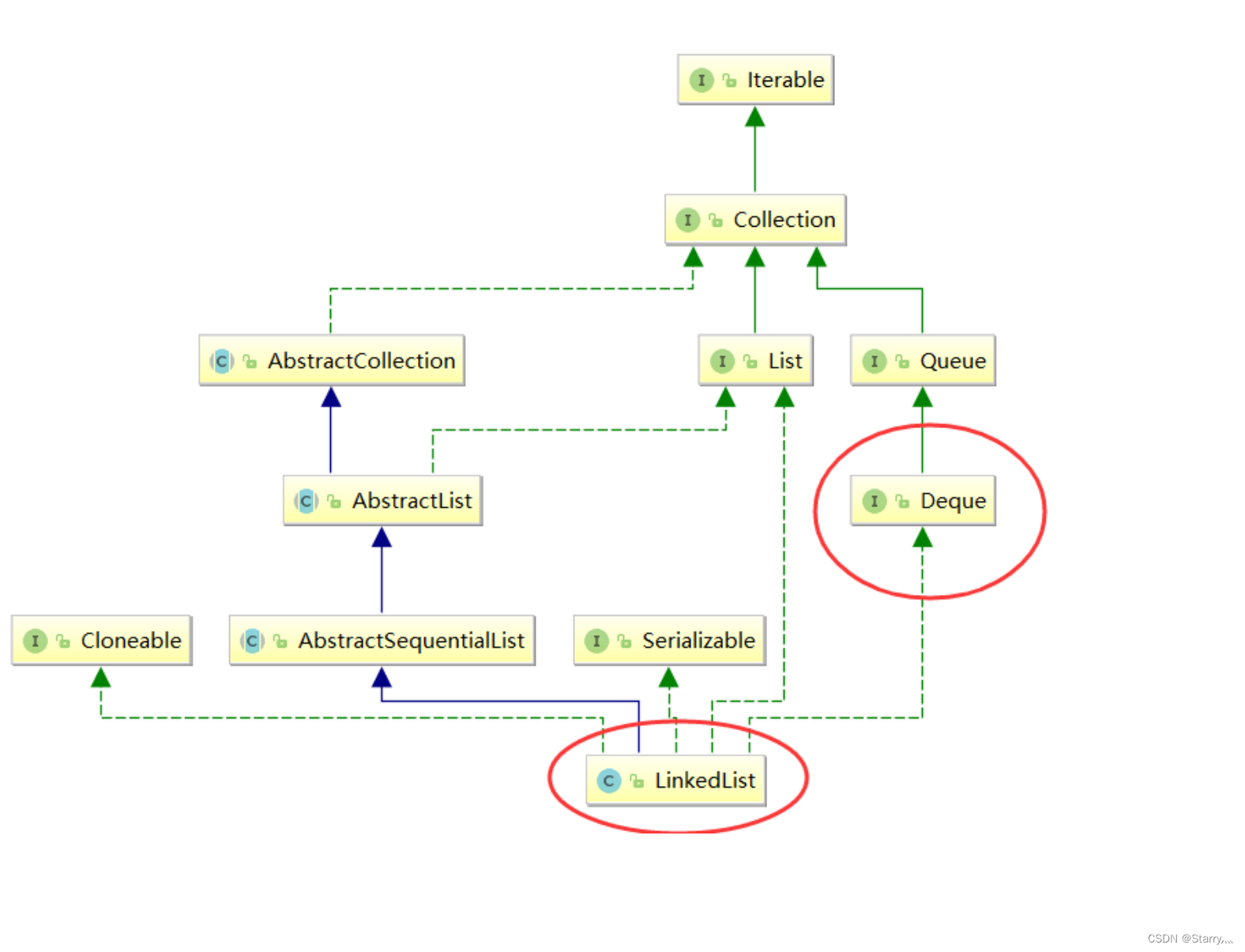
数据结构线性表-栈和队列的实现
1. 栈(Stack) 1.1 概念 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈 顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。 …...

IntelliJ IDEA 的 HTTP 客户端的高级用法
本心、输入输出、结果 文章目录 IntelliJ IDEA 的 HTTP 客户端的高级用法前言HTTP 请求对 gRPC 请求的支持对 GraphQL 和 WebSocket 请求的支持环境文件OpenAPI 补全用于持续集成的 HTTP 客户端 CLI花有重开日,人无再少年实践是检验真理的唯一标准IntelliJ IDEA 的 HTTP 客户端…...

代码随想录算法训练营第四十六天 _ 动态规划_198.打家劫舍、213.打家劫舍II、337.打家劫舍 III。
学习目标: 动态规划五部曲: ① 确定dp[i]的含义 ② 求递推公式 ③ dp数组如何初始化 ④ 确定遍历顺序 ⑤ 打印递归数组 ---- 调试 引用自代码随想录! 60天训练营打卡计划! 学习内容: 198.打家劫舍 动态规划五步曲&a…...

ffmpeg编译问题
利用ffmpeg实现一个播放器,ffmpeg提供动态库,但是编译链接的时候遇到下面的问题: ../ffmpegWidgetPlayer/videoplayerwidget.cpp:23: error: undefined reference to sws_freeContext(SwsContext*) ../ffmpegWidgetPlayer/videoplayerwidget.…...
-window、distinct、join等)
【flink番外篇】1、flink的23种常用算子介绍及详细示例(3)-window、distinct、join等
Flink 系列文章 一、Flink 专栏 Flink 专栏系统介绍某一知识点,并辅以具体的示例进行说明。 1、Flink 部署系列 本部分介绍Flink的部署、配置相关基础内容。 2、Flink基础系列 本部分介绍Flink 的基础部分,比如术语、架构、编程模型、编程指南、基本的…...

centos7做gitlab数据灾备项目地址指向问题
如果你在 CentOS 7 上使用 GitLab 时,它回复的数据指向了另一个服务器的地址,可能是因为配置文件中的一些设置不正确。 要解决这个问题,可以尝试以下几个步骤: 检查 GitLab 配置文件:打开 GitLab 的配置文件…...

leetcode:93. 复原 IP 地址
复原 IP 地址 中等 1.4K 相关企业 有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 ‘.’ 分隔。 例如:“0.1.2.201” 和 “192.168.1.1” 是 有效 IP 地址,但…...

玄子Share-CSS3 弹性布局知识手册
玄子Share-CSS3 弹性布局知识手册 Flexbox Layout(弹性盒布局)是一种在 CSS 中用于设计复杂布局结构的模型。它提供了更加高效、简便的方式来对容器内的子元素进行排列、对齐和分布 主轴和交叉轴 使用弹性布局,最重要的一个概念就是主轴与…...
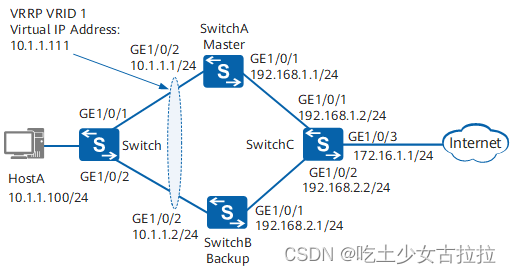
Nat easy IP ACL
0表示匹配,1表示任意(主机位0.0.0.255(255主机位)) rule deny source 192.168.2.1 0 设置拒绝192.168.2.1的主机通过 记住将其应用到接口上 [AR2]acl 2000 //创建基本ACL [AR2-acl-basic-2000]rule deny source 192…...

Numpy数组的数据类型汇总 (第4讲)
Numpy数组的数据类型 (第4讲) 🍹博主 侯小啾 感谢您的支持与信赖。☀️ 🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ�…...

通讯app:
为了开发一个即时通讯的app,包含发送文字、语音、视频以及视频通话的功能,我们需要考虑以下的技术栈和实现步骤: 技术栈建议: 前端:React Native 或 Flutter 用于跨平台移动应用开发。后端:ThinkPHP Wor…...

【Backbone】TransNeXt:最新ViT模型(原理+常用神经网络汇总)
文章目录 一、近几年神经网络 Backbone 回顾1.Densenet 与 Resnet2.CBP3.SENet4.GCNet5.DANet6.PANet 与 FPN7.ASPP8.SPP-net9.PSP-net10.ECA-Net 二、TransNeXt(2023)1.提出问题2.Aggregated Pixel-focused Attention2.1 Pixel-focused Attention&#…...
使用Java将图片添加到Excel的几种方式
1、超链接 使用POI,依赖如下 <dependency><groupId>org.apache.poi</groupId><artifactId>poi</artifactId><version>4.1.2</version></dependency>Java代码如下,运行该程序它会在桌面创建ImageLinks.xlsx文件。 …...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...
